用整体教学追求直观与逻辑的融合发展
吴增生




摘 要:在第十四届国际数学教育大会上,中国教育学会中学数学教学专业委员会举办了“平面几何优秀课展示与研讨”这一中国特色主题活动,以“平行线的判定与性质”一课为例,向国际同行介绍了中国式课例研究活动及中国教研体系特色.“平行线的判定与性质”教学案例集中体现了“用整体教学追求学生直观与逻辑融合发展”的教学特色,具体体现为:用“怎样研究一类几何图形”大观念,采用单元整体教学,引领学生一气呵成地研究平行线的定义、性质和判定,然后通过说理练习加以巩固;开展直观与逻辑融合的教学活动,发展学生的空间观念、几何直观和逻辑推理能力;围绕研究主题,有层次地开展研究活动,建立局部知识的逻辑结构体系.
关键词:中国几何教学;直观与逻辑融合;教学活动
在2021年7月11—18日举行的第十四届国际数学教育大会上,中国教育学会中学数学教学专业委员会举办了“一节平面几何课的展示与讨论”这一中国特色主题活动,以义务教育初中阶段平行线内容的教学为例,进行课例展示与研讨,并介绍了中国教研体系的运作特色及中国式课例研究的特点. 这一活动受到了国内外数学教育工作者的广泛关注.
由上海宋庆龄学校陈建豪教师(以下统称“执教教师”)执教的“平行线的判定与性质”一课,采用单元整体教学策略,在80分钟的教学过程中,引领学生自然合理地引入研究对象、提出研究问题、整体规划研究思路并分步实施,较好地体现了平面几何的核心育人价值——发展学生的空间观念、建立初步的几何直观、发展逻辑推理能力.
一、教材中教学内容的呈现方式
“平行线的判定与性质”一课的教学内容选自沪教版《九年义务教育课本·数学》七年级第二学期(以下统称“教材”)第十三章“相交线 平行线”. 该章内容是在学生认识了直线、射线、线段、角等基本几何元素的基础上,研究平面内两条直线的位置关系——相交与平行.“平行线”单元是在“相交线”单元学习用角刻画两相交直线相对位置关系及“三线八角”的基础上,进一步研究用角的数量关系刻画平面内两条直线的平行关系.
在“相交线”单元内容中,教材设计了“三线八角”的教学内容,这为平行线的研究提供了用角的数量关系刻画直线平行位置关系的直观工具和逻辑基础.
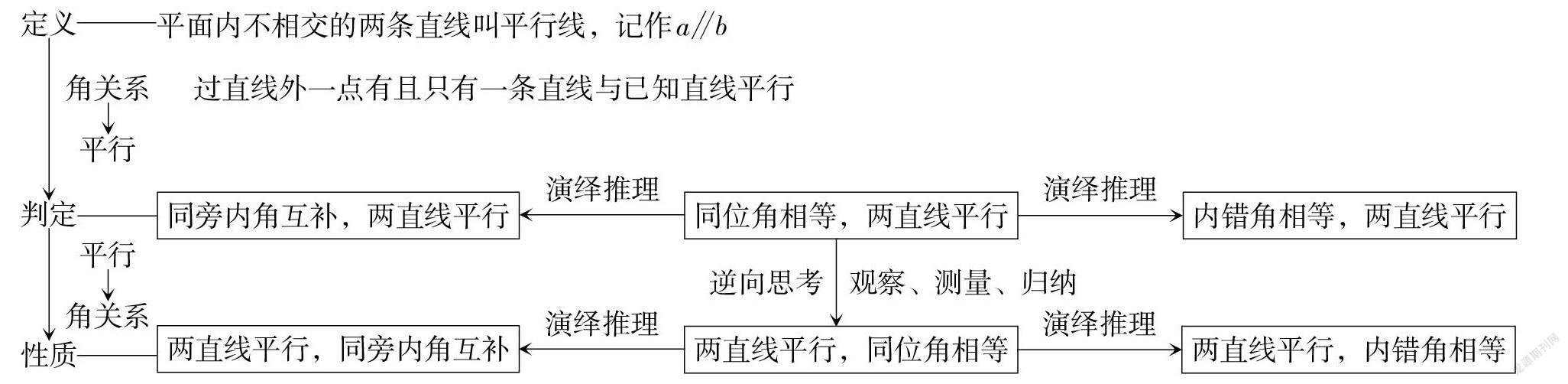
“平行线”教材内容的设计,是基于学生在小学阶段的认知基础,先给出“平行线”的概念,再利平推法画平行线这一操作活动形成直观经验,并进一步通过想象和归纳获得基本事实“同位角相等,两直线平行”及“过直线外一点有且只有一条直线与已知直线平行”. 在基本事实“同位角相等,两直线平行”的基础上,通过逻辑推理得到“内错角相等,两直线平行”和“同旁内角互补,两直线平行”. 然后研究“如果以两条直线平行为条件,同位角、內错角、同旁内角会有什么特殊关系”,并通过操作活动探究“两直线平行,同位角相等”. 在此基础上,通过逻辑推理获得“两直线平行,内错角相等”“两直线平行,同旁内角互补”. 教材采用“知识点 + 练习巩固”的形式穿插安排教学内容,教学课时安排建议如下表所示.
[单元内容 教学内容 教材建议课时 平行线 平行线的判定 5课时 平行线的性质 3课时 ]
二、课例简介
执教教师展示的“平行线的判定与性质”整体教学课例,用两节连排课,引导学生经历平行线的引入、定义、判定与性质研究的完整过程,并在教学后配4节习题课,总课时数上少于建议课时,且因其研究性,使得对学生空间观念、几何直观和推理训练取得了更好的效果. 特别地,让学生学会了怎样自然合理地引入研究对象、提出研究主题、规划研究主线、分步研究、建构逻辑体系. 事实上,这是在追求高阶认知能力的发展.
1. 基于已有经验和空间视觉直观,引入研究对象,发现和提出研究主题,规划研究思路
首先,执教教师引导学生回顾相交线的研究历程,基于相交线的位置的动态变化,提炼出“通过交角的特殊化引入垂线研究”的问题发现和提出经验(如图1).
[四个角][和为180°][相等][邻补角][对顶角][特殊化][两条直线垂直][两条直线相交] [位置关系][数量关系][图1]
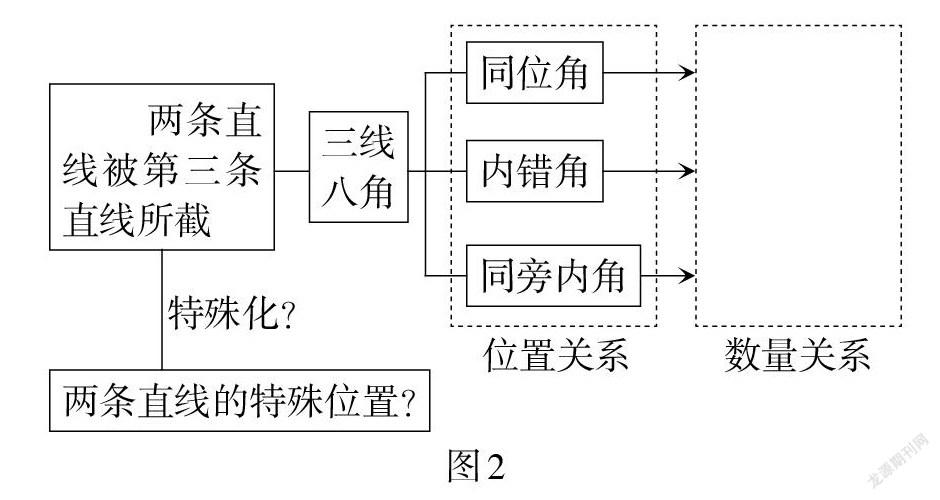
接着,引导学生回顾“三线八角”,明确这是在相交线基础上增加一条直线得到的,并引导学生思考“类似基于相交线提出垂线研究问题,能否基于两条直线被第三条直线所截,把这两条直线的位置特殊化,提出新的研究问题”,并结合一条直线方向的动态变化,提出并明确研究问题:什么是平行线?怎样判定两条直线平行?进一步,类比垂线的研究,规划平行线判定的研究主线:定义——从角的数量关系研究平行线的判定(如图2).
[ 两条直线被第三条直线所截][三线
八角][同位角][内错角][同旁内角][特殊化?][两条直线的特殊位置?] [位置关系] [数量关系] [图2]
2. 基于空间视觉直观和已有经验,抽象平行线的概念
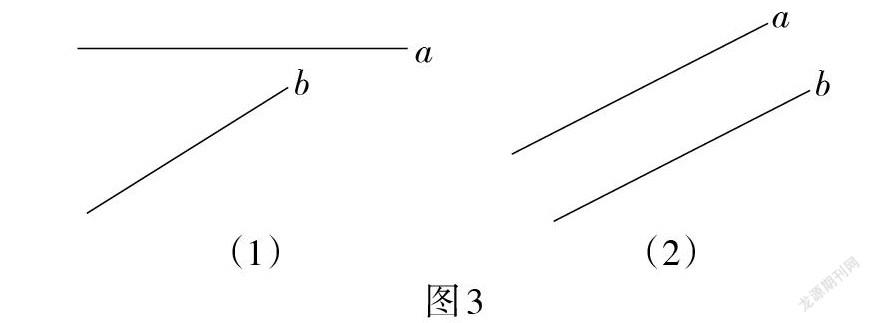
怎样给出平行线的定义?其实,学生在小学阶段已经学过平行线的定义,在这里是回顾性的. 但是,课例不能只停留在简单回顾上,而是要通过观察不同位置的两条直线,让学生直观判断其是否平行(如图3),以加深对平行线概念的理解. 同时,发现用定义判断两条直线平行的困难,引导学生提出“如何寻找更可靠、方便的判定两条直线平行的方法”的问题,进而引入后面的探究活动. [b][a][(1)] [a][b][(2)][图3]
3. 基于操作直观,确立基本事实
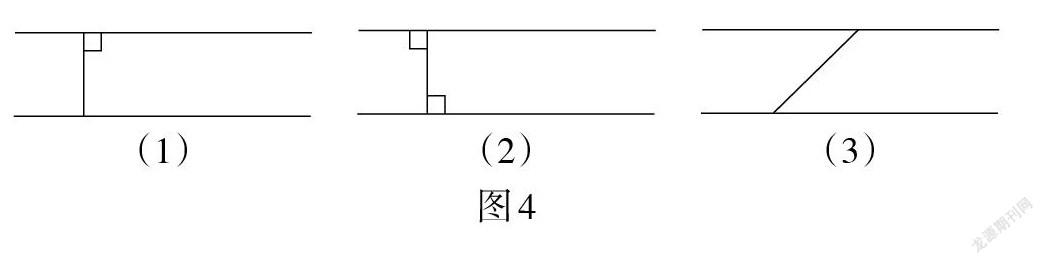
基于用定义判断两条直线平行的困难,执教教师让学生自主选择不同的方法画平行线,在这种直观操作的基础上,结合想象,确立平行线判定的基本事实,并得到平行公理. 学生给出了如图4所示的不同画法,这既为归纳得到平行线判定的基本事实提供直观启发,也为后面从内错角和同旁内角视角研究平行线的判定埋下伏笔.
接着,执教教师重点介绍平推法画平行线. 让学生用不同的方法平推画平行线,让同位角从特殊的直角出发,先利用三角板中的30°,45°,60°角,实现从直角到非直角的初步一般化;再利用任意角度的自制三角板推平行线,并引导学生关注推平行线时保证的是同位角始终相等,把这种画法推广到一般. 在画的基础上分析作平行线过程的本质,归纳出画相等的同位角即可作出平行线,进而得出平行线判定基本事实——同位角相等,两直线平行. 并进一步概括出平行公理——过直线外一点有且只有一条直线与已知直线平行.
4. 基于演绎推理,得到等价判定方法
有了平行线判定的基本事实,执教教师引导学生用演绎推理的方式,以平行线判定基本事实为依据,推出“内错角相等,两直线平行”“同旁内角互补,两直线平行”. 在这个过程中,执教教师讲解推理的要求——从条件出发,用已有的正确陈述为依据,推出结论. 通过教师示范和师生互动让学生学会证明“内错角相等,两直线平行”,再让学生独立证明“同旁内角互补,两直线平行”,让学生从模仿推理过渡到有指导的独立推理. 在这个阶段,先用直观的方法获得基本事实,再用演绎推理的方法得到其余两个判定定理.
5. 融合直观与逻辑,研究平行线性质
在完成并总结平行线判定的研究基础上,执教教师进一步提出问题:如果已知两条直线平行,那么同位角有什么关系?指出这是以“平行”这一位置关系为出发点,研究角的数量关系. 然后,让学生在已经画出的平行线上任意画截线,通过测量和动画展示的方法,让学生直观获得平行线的性质——两直线平行,同位角相等. 这是直观的学习活动. 在此基础上,类比平行线判定的研究过程,引导学生用演绎推理的方法推出平行线的内错角相等、同旁内角互补. 实际上,是基于直观基础进行演绎推理.
6. 开展融合直观与逻辑的说理训练活动
教师通过以下融合直观与逻辑的推理训练活动,引导学生辨析题设与结论,采取适当的依据(判定或性质)进行推理,既促进学生巩固新知,又促进学生空间观念、几何直观和逻辑推理能力的发展.
(1)如图5所示.
(2)如图6所示.
7. 总结分享,整体构建逻辑体系
教师用以下三个问题引导学生回顾总结,建立知识之间的联系.
(1)我们研究的几何对象是什么?研究了哪些内容?
(2)这些知识之间有什么联系?
(3)还有哪些收获和体会?
三、课例特色
上述教学过程体现了“用整体教学追求直观与逻辑融合发展”的特色,具体体现在以下方面.
1. 基于直观经验,引入图形关系
教学中,执教教师借助两条直线从相交到垂直的从一般到特殊的变化,直观提出垂线的研究问题,引导学生通过类比,基于“三线八角”提出平行线的研究问题,这是基于直观经验和类比,发现和引入研究对象,提出研究问题的过程,是直观和逻辑融合的学习活动.
2. 一般观念引领,建构整体框架
在基于直观和类比引入平行线后,用“怎样研究一类几何图形”的大觀念引领,整体规划研究思路:给出定义,明确研究对象,研究其判定和性质;通过类比相交线和垂线的“用角刻画直线的位置关系”的研究方法,提出“用角的数量关系刻画两直线平行”这一研究方法. 这个过程是基于前面研究的直观经验,再进行类比和猜想,也是直观与逻辑融合的学习活动.
3. 语言符号表达,抽象几何概念
小学学过平行线的概念,教师通过设计直观想象判断两条直线是否平行的活动,让学生辨别平行线的概念,发现用定义判定平行线的困难. 定义回顾时基于语言并用符号表达,这是基于逻辑的. 而针对具体的图形进行辨别,则是把抽象的概念应用于直观图形,是直观与逻辑的融合.
4. 操作确认事实,形成逻辑基础
在“平行线的判定与性质”的研究中,“同位角相等,两直线平行”这一基本事实是推理得到其余两个判定及平行线性质的逻辑基础,这一逻辑基础的获得依赖于直观,是通过平推法画平行线活动获得的,而在这一直观经验获得的过程中,经历了同位角从特殊到一般的归纳过程,这又是逻辑推理活动.
5. 直观观察归纳,发现提出命题
在“内错角相等,两直线平行”“同旁内角互补,两直线平行”的教学中,执教教师基于学生开放画平行线留下的图形,借助“三线八角”的概念,通过归纳,发现和提出命题,并依据“同位角相等,两直线平行”这一基本事实进行推理证明. 在研究平行线性质的过程中,通过让学生在两平行线上任意画截线,测量同位角,动态展示截线的变化,通过归纳得到“两直线平行,同位角相等”.
6. 通过演绎证明,确立几何命题
在用基本事实推出其余两个判定和用“两直线平行,同位角相等”推出其余两个性质的教学中,通过执教教师讲解示范,学生模仿、独立操作和执教教师指导等活动,让学生学习“以条件为出发点,以基本事实和定理为依据,逐步推出结论”这一推理的逻辑话语体系,并通过练习加以巩固.
7. 逐步层次展开,构建知识体系
教学过程中,执教教师设计的研究活动,从直观经验开始,通过类比发现和提出问题,用几何图形研究的一般观念引领,整体规划研究思路和方法,并经历“定义—画图—确立基本事实—研究其余两个判定—研究平行线的性质”的过程,分步有序实施,最终通过课堂小结中的提问引导学生建立知识之间的联系. 整个过程结构清晰、层次分明、环环紧扣. 学生经历了完整的平行线研究过程,建构了知识的局部逻辑体系,获得了几何图形关系研究的数学活动经验.
四、教学设计的理论依据
这种直观与逻辑融合的整体教学设计,具有比较坚实的理论基础. 首先,欧几里得几何在促进学生空间观念、几何直观和逻辑推理能力发展中具有不可替代的作用,这也是初中平面几何教学的核心育人价值. 要实现这些核心育人价值,需要开展融合直观与逻辑的单元整体活动. 党中央、国务院在2019年6月颁布的《关于深化教育教学改革全面提高义务教育质量的意见》中所倡导的主题化、项目化学习方式,从政策层面说明了开展整体教学的重要性.
直观与逻辑融合是数学思维最显著的特征. 哲学家、数学家和数学教育家都有许多相关论述. 例如,德国著名哲学家康德说过,人类所有的知识始于直观,从哪里进入概念,以理念结束;Hanna G,de Villiers M说过,高水平的数学研究就是新定理的发现与证明;Elliott Whiteley指出,高水平的数学思维是直观洞察与严密分析的流畅转换(2011年);Giuseppe Longo认为,直观指的是“看到什么、能做什么”,而非“是什么”(2011年);史宁中指出,知识的发现依赖于直观,知识的确立依赖于逻辑.
直观与逻辑融合得到了认知心理学的支持. 数学逻辑推理能力是从知觉运动到核心概念,从直观与形式的混合推理到公理化形式化推理的循序渐进的成熟和发展的. 逻辑推理能力的发展是基于直观想象的(如图7).
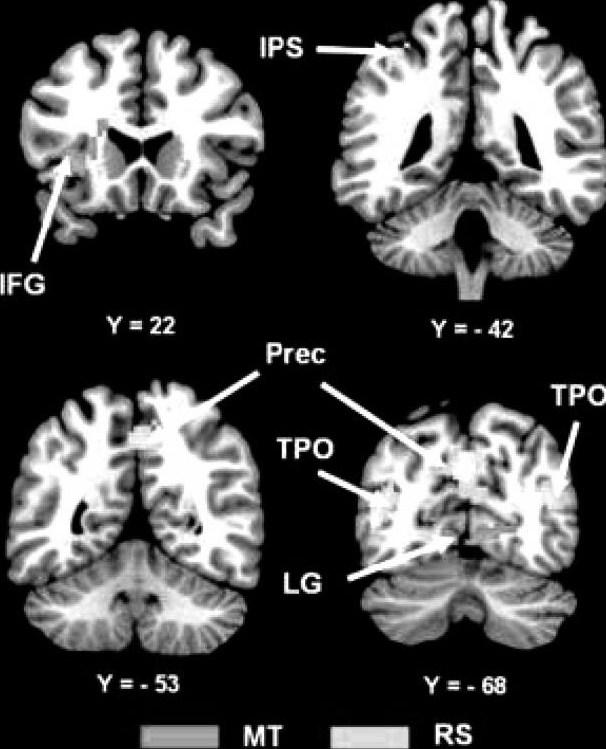
直观与逻辑融合,得到脑科学相关理论的支持. 心理逻辑理论(MLT)认为,演绎推理基于语义加工(Braine and O'Brien,1998年;Rips,1994年;Goel et al.,2000年;Noveck et al.,2004年);周新林等也认为,几何证明与几何计算相比,更多激活了大脑语义网络(如图8).
如图9,心理模型理论(MMT)认为,演绎推理基于视觉空间加工(Johnson-Laird,1983年,2001年,2006年;Johnson-Laird and Byrne,1991年).
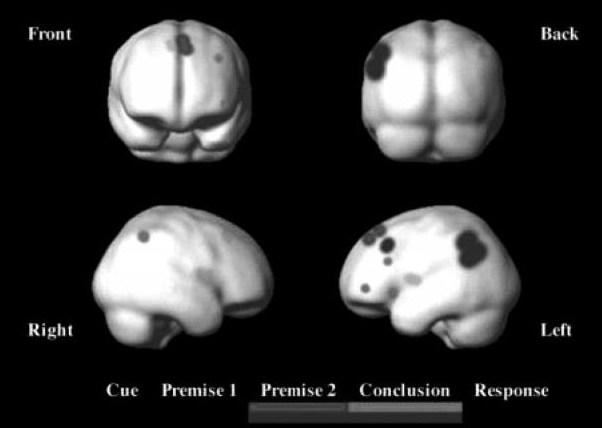
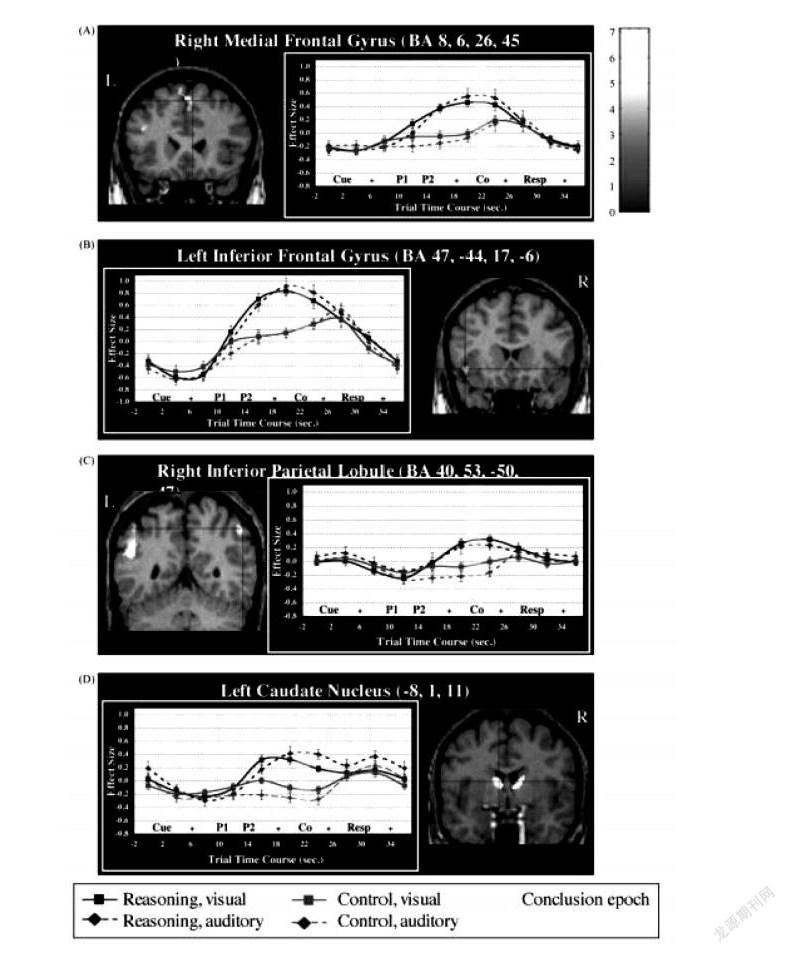
双加工理论认为,不同的演绎推理任务依赖于不同类型的神经环路,基于情境的推理更多地激活语义网络,而基于空间的推理更多地激活空间网络(Johnson-Laird,1983年,2001年,2006年;Johnson-Laird and Byrne,1991年). 而超模态理论认为,语义和视觉空间整合于演绎推理超模态的不同阶段(如图10,图11).
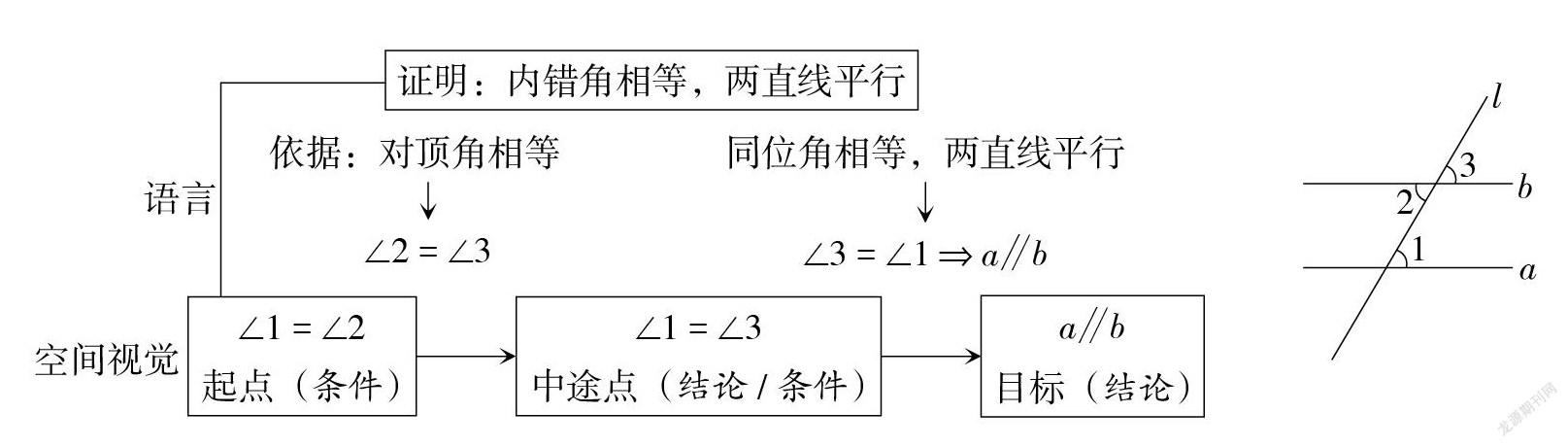
根据演绎推理的超模态理论,直观与语义在演绎推理的不同环节起到作用. 那么,具体是怎样融合的呢?图12以证明“内错角相等,两直线平行”的探究过程为例,分析了演绎证明过程中语义与空间加工在什么时候,怎样起作用. 结果表明,在理清命题的题设和结论,在证明推理过程中回顾证明所依据的原理时,语言加工起到主要作用. 但是,语言的这种作用是嵌入到证明思路的总体规划活动中的. 也就是说,演绎证明就是从题设出发,以已经确立的命题为推理依据,架构从起点通向目标的桥梁,这一过程整体上是直观的空间加工,而在搜索原理的过程中,需要在适当的地方插入命题的语义加工.
五、进一步完善的建议
教学既要讲究科学,也是不断完善中的艺术. 本课例的教学中仍然存在可以进一步完善之处,具体体现在以下几个方面.
1. 问题提出的整体性可以更强
基于“三线八角”,在通过两条直线的位置关系的特殊化引入平行线后,可以更具有整体性地提出问题:类比相交线的研究,怎样定义平行线?用什么几何量刻画两条直线的平行关系?在回顾平行线的定义,发现依据定义判定两条直线平行的困难后,可以进一步提出正反两方面的问题:怎样判断两条直线平行?怎样判断两条直线不平行(实际上是性质).
2. 可以进一步通过可视化表达思考过程
例如,可以用图13表示平行线判定的研究思路,用图14表示平行线性质的研究思路,最终整合成图15所示的“平行线判定与性质”的整体研究思路,更直观地总结思考过程,表达知识结构体系.
六、研究结论
基于前文分析,可以得到融合直观与逻辑的初中平面几何单元整体教学的以下基本策略.
基本策略1:基于知觉运动,形成充分的直观经验.
基本策略2:用好语言中介,抽象几何概念与命题.
基本策略3:一般观念引领,基于演绎推理构建局部知识体系. 所谓一般观念,指的是怎样研究几何图形及其关系,包括研究思路、研究内容和研究方法等.
融合直观与逻辑的整体教学,既要求直观与逻辑融合,又要求进行整体教学. 其最显著的特征是:几何研究基于图形直观进行逻辑推理,整体教学聚焦核心问题,规划研究主线、分步实施、逐步发展.
这种直观与逻辑融合的单元整体教学策略,可以应用到几乎所有几何图形及其关系的教学实践中. 因为它既具有直观性,又强调逻辑推理,还强调研究的完整性和系统性,这对学生空间观念的形成、几何直观的建立及推理能力的发展都具有良好的效果.
参考文献:
[1]伊曼努尔·康德. 纯粹理性批判[M]. 邓晓芒,译. 北京:人民出版社,2017.
[2]HANNA G,De VILLIERS M. Proof and Proving in Mathematics Education:The 19th ICMI Study[M]. Dordrecht:Springer Nature,2012.
[3]史寧中. 数学的抽象[J]. 东北师大学报(哲学社会科学版),2008(5):169-181.
[4]RODRIGUEZ-MORENO D,HIRSCH J. The dynamics of deductive reasoning:An fMRI investigation[J]. Neuropsychologia,2009,47(4):949-961.

