肼类燃料与NO2气相抽氢的反应动力学模拟

赵建铄，黄智勇，金国锋，高敏娜，祝慧鑫

（火箭军工程大学导弹工程学院，陕西 西安 710025）

1 引言

肼类燃料是目前广泛应用的液体推进剂，包括肼（N2H4）、甲基肼（MMH）与偏二甲肼（UDMH），它与四氧化二氮（N2O4）组成常用的双组元自燃推进剂，广泛应用于航天发射中［1］，在世界航天建设发展中发挥着重要作用。双组元自燃推进剂是通过燃料与氧化剂接触自发引燃的推进剂［2-3］，其自燃性不仅使推进系统结构相对简单，而且可提高再着火的可靠性［4］，其中影响双组元自燃推进剂研发和选择的重要参数之一是着火延迟期。着火延迟期定义为氧化剂与燃料从相互接触到开始出现火焰的时间间隔，受多种因素的影响［5］，如果着火延迟期太长，则推进剂在燃烧室中发生积累，着火时会引起一个大的压力尖峰，导致发动机结构的损坏甚至被摧毁。

近年来研究较热的绿色推进剂，如：N，N，N′，N′-四甲基乙二胺［6］（TMEDA）、硝酸羟胺［7］（HAN）与N，N⁃二甲基叠氮乙基胺［8］（DMAZ），受制于较长的着火延迟期未能大范围的应用。由于实验只能测定着火延迟期，目前在降低着火延迟期的研究鲜有实质的进展，而密度泛函理论由于可以模拟分子反应，对反应的机理进行分析，为优化反应过程提供指导，近年来在分子反应机理领域迅速发展并被广泛应用。

2011 年，Liu Wei-Guang［9］等用密度泛函理论确定了纯硝酸（NA）与TMEDA 反应的机理，提出影响着火延迟期的因素之一是NA 分解产生的NO2与TMEDA 的抽氢反应；2013 年，Liu Wei-Guang［10］又采用镀金室反应器，在298.15 K、1.01×105Pa N2条件下，进行MMH 与氧化剂NO2/N2O4的反应，提出在N2环境下MMH 的氧化机理之一是NO2连续提取H原子并形成HONO；2014 年，Chen C C［11］等根据量子化学模型和过渡态理论的结果，同样分析表明，着火延迟的差异是由于NO2从燃料中提取H 原子的反应速率不同。在肼类燃料与N2O4的反应过程中，简略分为液相与气相两个部分，首先是与N2O4液相的放热反应，放热使得N2O4分解产生NO2，其次是与NO2气相的反应。目前对于NO2气相抽氢反应的势垒、反应速率与着火延迟期的关系的研究，缺乏详细的阐述，因此对抽氢反应进行研究来分析着火延迟期有着重要作用。

本研究基于密度泛函理论，对N2H4、MMH 与UDMH 三种肼类燃料与NO2的反应过程进行模拟，分别在反应活性、反应位点以及抽氢反应的势能面与反应速率常数进行探讨，进而研究肼类燃料与NO2的反应机理，通过分析影响着火延迟期的因素，为设计研发具有较低着火延迟期的新型推进剂提供参考。

2 计算方法

首先在B3LYP/6-31+G（d，p）［12］理论水平下，优化肼类燃料的几何构象，产生带有波函数信息的文件，然后以波函数分析为基础［13-14］，通过简缩福井函数（Condensed Fukui function）与平均局部离子化能（Average local ionization energy，ALIE）来预测反应活性位点［15］。

接下来在B3LYP/6-31+G（d）理论水平下，优化N2H4、MMH、UDMH 与NO2反应路径中的反应物、产物、过渡态及中间体的几何构象，然后在B2PLYP/def2tzvp 水平上对其进行单点能计算。通过对优化构象的频率分析，确认所得的反应物、产物及中间体频率都为正值，过渡态有且仅有一个虚频。此外，运用内禀反应坐标（IRC）对所有的过渡态进行确认，计算借助multiwfn［16］程序包与Gaussian 09 程序包［17］完成。

最后采用传统过渡态理论（TST）［18-19］计算反应速率常数，其计算公式为：

式中，K（T）为反应速率常数，L·s-1·mol-1；k（T）为隧道效应校正因子，无量纲；σ为分子对称数，无量纲；kB为玻尔兹曼常数，J·K-1；h 为普朗克常数，J·s；R 为理想气体状态常数，J·mol-1·K-1；T为温度，K；Pθ为标准大气压，Pa；ΔG为反应吉布斯自由能能垒，kJ·mol-1；根据过渡态虚频的绝对值v#，cm-1；利用Wigner 方法［20］计算隧道效应校正因子，公式为：

3 结果与讨论

3.1 反应活性

20 世纪50 年代，福井谦一提出前线轨道理论［21］，其中指出在分子中，最高占有轨道（HOMO）上的电子能量最高，所受束缚最小，最容易发生还原反应；而分子的最低空轨道（LUMO）在所有的未占轨道中能量最低，最容易接受电子，给电子能力最强，最容易发生氧化反应。HOMO 与LUMO 二者的能量之差ΔE（gap），反映的是分子与自由基反应的活性大小［22］。基于B3LYP/6-31+G（d，p）对N2H4、MMH 与UDMH 进行几何优化，其分子结构如图1 所示。

图1 N2H4、MMH 与UDMH 的几何构型Fig.1 Geometric configurations of N2H4，MMH and UDMH

计算得到其最高占有轨道能量与最低空轨道能量，结果如表1 所示。

由表1 可以看出轨道能量之差N2H4>MMH>UDMH，表明UDMH 的反应活性较大，可以推测出在3 种肼类燃料中，UDMH 与NO2自由基的反应更快。分析其原因为分子结构，因此对肼类燃料进行了N（1）─H键的测定，如表2 所示，MMH 的一个甲基与UDMH 的两个甲基分别从分子N（1）─H 键中提取电子密度，这使得MMH 与UDMH 的N（1）─H 键长更长，键解离能更小，从而更快的引发着火反应。2003 年，Hampton C等［5］测定了3 种肼类燃料与红烟硝酸的着火延迟期，结果表明UDMH 比N2H4的着火延迟期快73%，结果与理论计算一致，表明使用反应活性大小来判断着火延迟期长短是可行的。

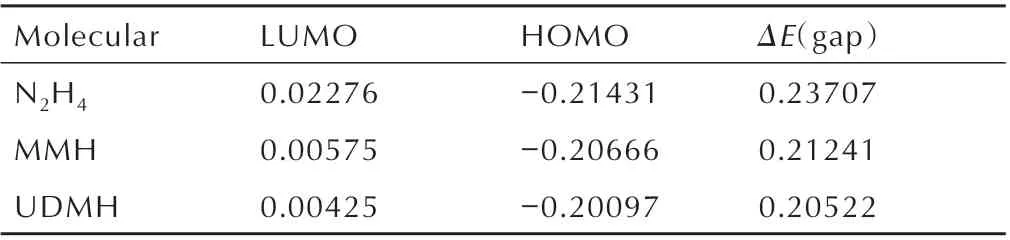
表1 N2H4、MMH 与UDMH 的最高占有轨道能量、最低空轨道能量及能量差Table 1 The highest occupied orbital energy，the lowest vacant orbital energy and the energy difference of N2H4，MMH and UDMHeV

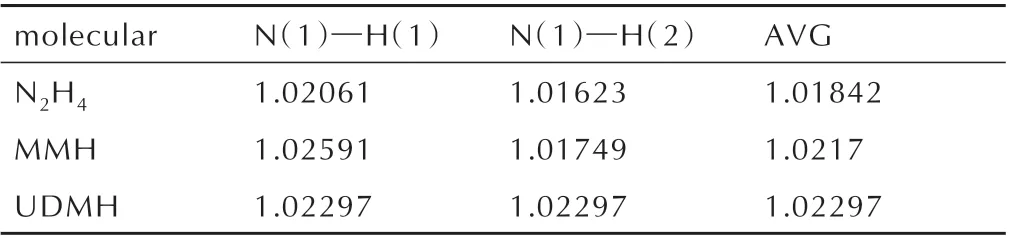
表2 N2H4、MMH 与UDMH 的N（1）─H 键长Table 2 N（1）─H bond length of N2H4，MMH and UDMH Å

3.2 反应位点

3.2.1 简缩福井函数

福井函数［15］可表示空间中某一点的电子密度对电子数的偏微分结果，作为实空间函数常用来预测反应活性位点，共为3 类，分别用于预测亲核、亲电、自由基反应区域。为了定量考察每个原子上福井函数的分布量来预测自由基的反应位点，可计算其原子的简缩福井函数，数值越大，则说明自由基反应越容易发生在该原子上。通过简缩福井函数的计算，确定肼类燃料与NO2自由基反应时的活性位点。通过Hirshfeld 电荷求差来计算肼类燃料的简缩福井函数f0，结果如表3 所示。

由于肼分子属于对称性结构，N（1）与N（4）的反应活性是相同的，同时由表3 可知，测定的简缩福井函数f0 值都为0.2225，可以看出计算值与实际结构符合。从MMH 和UDMH 的简缩福井函数可以看出，MMH 中N（1）的值较N（4）值大0.0113，表明N（1）可能为活性位点；UDMH 中N（1）的值较N（4）值大0.0161，表明N（1）可能为活性位点，两个C 原子的简缩福井函数相差0.0001，结果符合UDMH 的对称性结构性质。

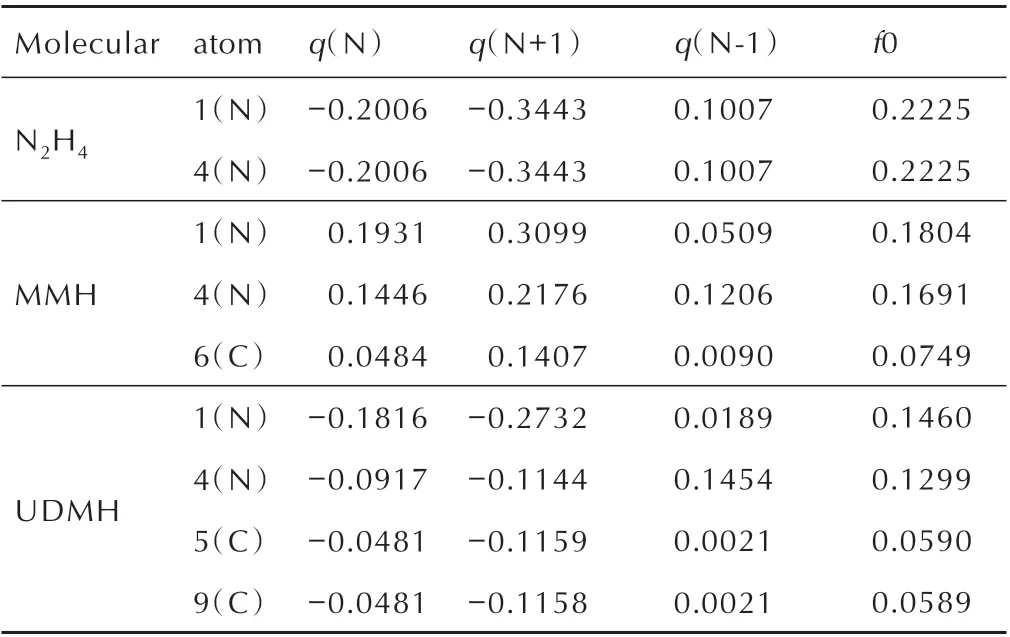
表3 N2H4、MMH 与UDMH 中重原子的Hirshfeld 电荷与简缩福井函数值Table 3 Hirshfeld charges and reduced fukui function values of heavy atoms in N2H4，MMH and UDMHe

对比同一分子的N 原子与C 原子的简缩福井函数，可以看出，N 原子的反应活性大于C 原子，原因在于N 原子存在孤对电子，孤对电子存在不稳定性，同时N─H 键的键能小于C─H 键的键能，N 原子更容易进行化学反应。

3.2.2 ALIE

从分子构成的系统空间的某点移去一个电子所需要的能量被称为“ALIE”［23］，其最小值显示了最不稳定的电子的位置，在分子表面上，ALIE 越小处，由于电子束缚得越弱，其电子活性越强，就越容易发生自由基反应。基于产生的波函数文件，计算可得电子密度为0.0005 a.u.的等值面，如图2 所示，红色区域为分子的ALIE 数值较大区域，蓝色区域为分子的ALIE 数值较小区域，青色小圆球则代表区域内的极小值点。

从图2 可以看出，N2H4的N（1）与N（4）附近分布相同，其最小值为0.255 a.u.；MMH 的N（1）附近分布区域较N（4）大，其最小值为0.246 a.u.；UDMH 的N（1）附近分布区域较N（4）大，其最小值为0.240 a.u.。

图2 N2H4、MMH 与UDMH 的ALIE 等值面Fig.2 ALIE isosurfaces of N2H4，MMH and UDMH

对比3 种肼类燃料，可以看出UDMH 的最小值0.240 a.u.为最小的，同时蓝色区域为最大的，也反映出UDMH 的反应活性最大。

简缩福井函数与ALIE 方法的计算结果一致，可以得出：在3 种肼类燃料中，N2H4活性位点为N（1）或N（4），MMH 活性位点为N（1），UDMH 活性位点为N（1），分析肼类燃料的活性位点，对构建反应过程势能面有着重要的作用，为NO2的抽氢反应提供理论计算基础。

3.3 抽氢反应

3.3.1 势能面

根据简缩福井函数与ALIE 方法判断肼类燃料对NO2自由基反应的活性位点，接下来针对N2H4的N（1）或N（4）原子、MMH 的N（1）与UDMH 的N（1）与NO2自由基发生的反应过程，构建了抽氢反应路径。按照NO2的抽氢产物的不同构型分别为顺式（cis-HONO）、HNO2与反式（trans-HONO），如图3所示。

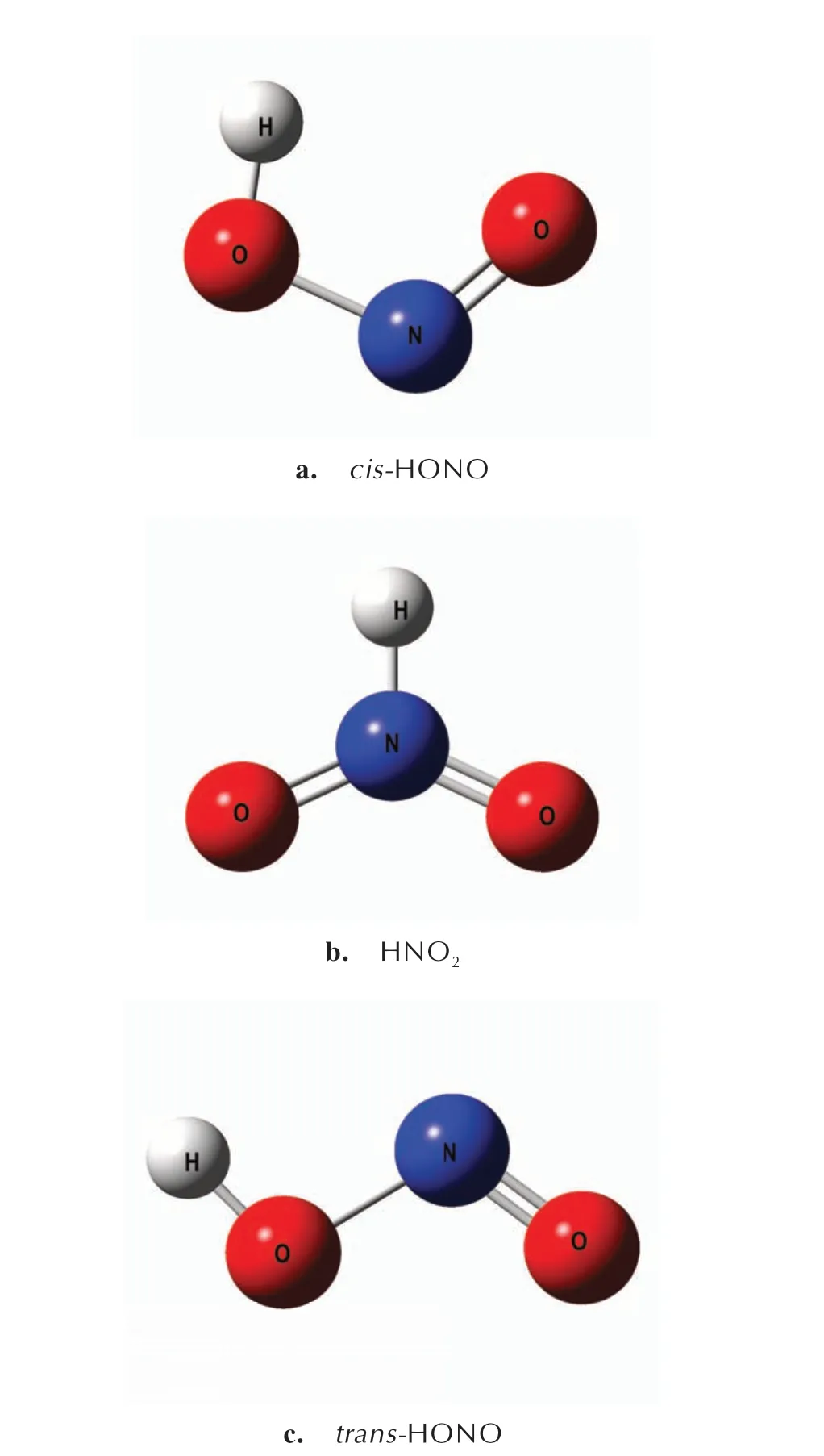
图3 cis-HONO、HNO2与trans-HONO 的几何构象Fig.3 Geometric conformation of cis-HONO，HNO2 and trans-HONO

在B3LYP/6-31+G（d）理论水平下，计算N2H4、MMH、UDMH 与NO2的抽氢反应路径，如表4 所示。

从表4 可以看出，在N2H4与NO2抽氢反应中，生成cis-HONO 的势垒为23.544 kJ·mol-1，为3 条路径中势垒最小的，HNO2的势垒为38.505 kJ·mol-1，为3条路径中势垒最大的，trans-HONO 的势垒为34.982 kJ·mol-1左右，介于中间值。cis-HONO 型产物的势垒较低，因此在进行抽氢反应时，首先越过cis-HONO 这个低势垒反应，在室温下反应cis-HONO 比HNO2和trans-HONO 容易发生，结果为反应产物主要集中是cis-HONO，分析为其能量较trans-HONO 与HNO2低，cis-HONO 物质较稳定，因此反应路径更容易发生。同样，在MMH、UDMH 与NO2抽氢反应中，生成的反应产物主要为cis-HONO。

表4 在298.15 K 下N2H4、MMH、UDMH 与NO2 抽氢反应的物质相对焓值Table 4 Relative enthalpy values of N2H4，MMH，UDMH and NO2 hydrogen extraction reaction at 298.15 KkJ·mol-1

在肼类燃料与NO2的反应过程中抽氢反应是一个引发反应，势垒较低的cis-HONO 发挥着决定性作用，生成cis-HONO 的快慢决定了着火延迟期的大小，接下来对比分析N2H4、MMH、UDMH 与NO2生成cis-HONO 的抽氢反应势能面，如图4 所示。

从图4 中看出相对于MMH 的25.442 kJ·mol-1与N2H4的27.659 kJ·mol-1的反应焓，UDMH 的反应焓为13.751 kJ·mol-1，意味着反应过程吸热少，更有利于在低温条件下反应的进行。与此同时，UDMH 的抽氢势垒最小，为3.589 kJ·mol-1，MMH 次之，为15.954 kJ·mol-1，N2H4最大，为23.544 kJ·mol-1。针对火箭发动机运作处于常温或低温的外部环境，在3种肼类燃料中，UDMH 与NO2在发生反应时，需要越过的能垒低，能够与NO2更快的进行反应，较好的对应了其最短的着火延迟期。

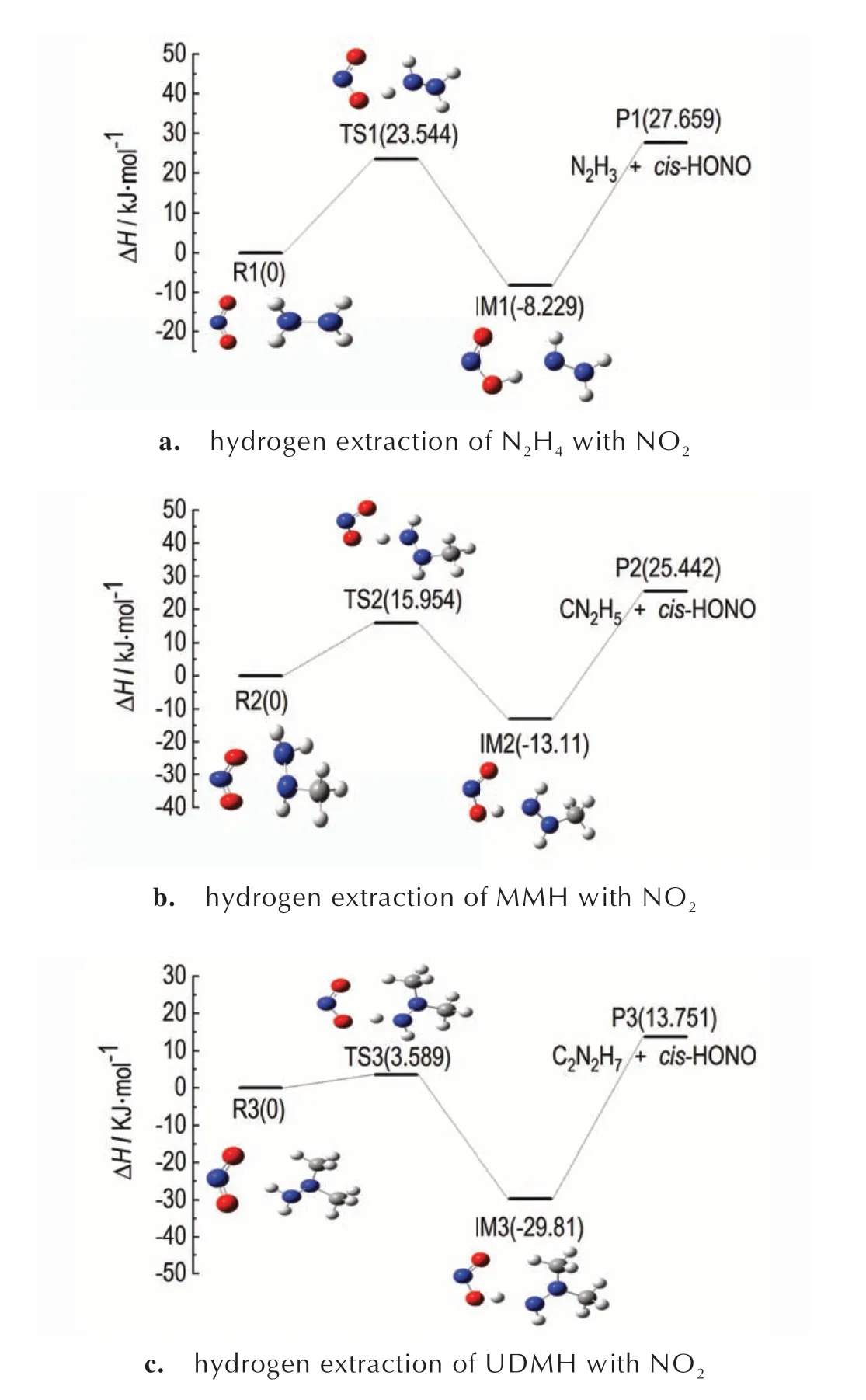
图4 N2H4、MMH、UDMH 和NO2 生成cis-HONO 的抽氢反应势能面Fig.4 Potential energy surface of hydrogen extraction reaction for the formation of cis-HONO from N2H4，MMH，UDMH and NO2

3.3.2 反应速率

采用TST 理论，计算得抽氢反应的反应速率常数，如表5 所示。

从表5 看出，在N2H4与NO2的反应中，对于3 种不同的产物路径，cis-HONO 的反应速率常数为4.19×102L·s-1·mol-1，远大于trans-HONO 与HNO2的反应速率常数，表明N2H4与NO2的抽氢反应过程中，生成cis-HONO 的速率更快，主要产物为cis-HONO。同样，在MMH、UDMH 与NO2抽氢反应中，生成cis-HONO 的速率最快。

表5 在298.15 K 下N2H4、MMH、UDMH 和NO2 抽氢反应生成3 种构型的反应速率常数Table 5 Reaction rate constants of three configurations generated by the hydrogen extraction reaction of N2H4，MMH，UDMH and NO2 at 298.15 KL·s-1·mol-1

为了分析3 种肼类燃料与NO2的着火延迟期与抽氢反应速率的关系，分析了3 种肼类燃料生成cis-HONO 的反应速率常数，在3 种肼类燃料与NO2的反应中，UDMH 的反应速率常数为9.81×105L·s-1·mol-1，远大于MMH 与N2H4，表明在298.15 K 下3 种肼类燃料中，UDMH 与NO2生成cis-HONO 的反应更快，与UDMH 与NO2的着火延迟期相对较短的事实相符合。

4 结论

采用密度泛函理论方法对N2H4、MMH、UDMH的结构进行理论计算，从反应活性、活性位点、以及抽氢反应的势能面和反应速率常数进行了探究，得到主要结论如下：

（1）用肼类燃料反应活性的大小来预测着火延迟时间的长短具有可行性。在3 种肼类燃料中，UDMH的反应活性最高，表明UDMH 与NO2自由基反应更快。

（2）肼类燃料与NO2的抽氢反应中，cis-HONO 为主要产物，用反应的势垒与反应速率常数来预测着火延迟时间具有可行性。在3 种肼类燃料与NO2生成cis-HONO 的反应中，UDMH 的势垒最小，为3.589 kJ·mol-1，UDMH 的反应速率常数最大，为9.81×105L·s-1·mol-1。

（3）目前，可以通过复配的方法来降低新型推进剂的着火延迟期，但通过实验筛选存在工作量大且危险的问题，因此通过理论计算抽氢反应的势垒与反应速率常数，来达到初步筛选的目的，这对推进剂的设计与研发具有重要意义。