颗粒形状对砂性土宏细观力学性质的影响

薛明华，陈圣仟 ，杨世文

(1.济南市勘察测绘研究院，济南 250101；2.贵州省建筑设计研究院有限责任公司，贵阳 550000)

砂性土(无黏聚力)是由大量土颗粒构成的多体相互作用体系[1]。球形度(form or sphericity)、圆滑度/棱角度(roundness or angularity)、粗糙度(roughness)从3个不同尺度描述了颗粒的形态特征[2-3]，被认为是颗粒形状量化的基本指标[4]，用于评价颗粒的形状。另外，还衍生出诸如凹凸度(non-convexity)、长宽比(aspect ratio)等[5]另外一些颗粒形状评价指标。颗粒形状会对砂性土的宏观性质产生影响，如相对密实度、渗透特性、压缩特性、剪切强度及变形等[2-10]。而宏观上展现的力学特性本质上是细观尺度(颗粒层面)颗粒间相互作用的累积[4,11]。对于颗粒形状与砂性土宏观力学特性之间的关系，研究人员开展过大量的室内试验或数值模拟研究工作。试验研究认为，几乎所有砂性土的宏观力学特性都会受到颗粒形状的影响[2-4,11]。比如，颗粒的形状会影响砂性土的极限孔隙比(相对密实度)，多棱角、表面粗糙和球形度低的颗粒堆积体具有较大的极限孔隙比区间长度，相反，较光滑球形颗粒堆积体的极限孔隙比区间长度较小[2,12-14]。在三轴压缩试验、直剪试验中，相同密实度条件下，多棱角的砂性土比表面圆滑的砂性土具有较大的强度，且在峰值应力前具有较大变形模量[9,13]。当试样体积变形恒定时，表面圆滑的砂较表面多棱角的砂稳定性差，强度低[15]。临界状态下砂性土的内摩擦角、临界状态线的斜率、峰值内摩擦角以及峰值应力前砂性土的变形模量均随砂粒棱角度的增加而增加[9,16]。

多数室内或数值试验的研究阐明了不同颗粒形状会影响砂性土的强度和变形特性，但颗粒形状对砂性土强度和变形特性的影响机理则鲜有研究。室内试验具有明显的局限性，如颗粒的粗糙度、棱角度和球形度对砂性土宏观力学性质的影响很难做到实际意义上的分离[4,9,17]。制备由规则形状的颗粒构成的试样无疑脱离了天然砂性土中颗粒随机不规则形状的特性，且放大了颗粒形状的影响。在这种情况下，诸多学者对颗粒形状与砂性土力学特性的关系持不同意见，除了颗粒的球形度、圆滑度和粗糙度与砂性土力学特性的基本认识以外，有人认为颗粒形状对砂性土剪切强度的影响甚微[18]，有人指出颗粒形状是否对砂性土剪切强度产生影响尚不清楚[2]。

在此基础上，现通过室内直剪试验及其离散元模拟试验探索颗粒形状与砂性土力学特性，特别是强度与变形特性。研究对象是较为常见的砂性土，其颗粒为随机不规则形状，且在相同的试验条件下设计基于圆形颗粒的对比试验。

1 直剪试验

直剪试验的试样为天然硅质粗砂，其级配曲线如图1所示，不均匀系数为1.44。试样平均粒径为0.9 mm，密度为2.5 g/cm3，最大孔隙比1.076，最小孔隙比0.67，L/d50≈44>40且L/dmax≈18>15(L为试样的最小尺寸，d50为平均颗粒粒径，dmax为最大颗粒粒径)。根据文献[19-20]，试样的尺寸效应很小。

剪切盒总尺寸为60 mm×60 mm×43 mm(长×宽×高)，包括上下两盒。剪切过程采用应变控制式，剪切速率可在0.001～2 mm/min范围内自由调节，上盒固定，由电机推动下盒剪切，垂直压力通过杠杆悬挂载荷砝码施加。试验时，垂直和水平位移分别通过两个千分位移表读取，剪切力通过水平应力环采集，精度达±2.2 N。

制样时按照50%的相对密实度(中密)换算试样的质量，分层击实，最后平整试样的上表面，以较慢的剪速(约0.05 mm/min)在3种法向应力(22、50和100 kPa)下剪切。对应每种法向应力进行3个试样剪切，当2次试验结果差异很大时增加剪切试样进行剪切试验，每种法向应力下试验结果取3次试验的算术平均值。

2 模拟试验

2.1 粒径不同、细观结构相同试样生成方法

采用二维颗粒流离散元分析程序(particle flow code，PFC)模拟直剪试验。模拟直剪试验的理论基础参见文献[20]。模拟直剪试验的对象可以是具有不同长宽比的椭圆形颗粒[21]、边数可控制的多边形颗粒[22]，还可以是通过颗粒自动填充(computerized particle analysis,CPA)形成的任意形状的颗粒[23]。由于天然颗粒形状的复杂性，要实现模拟试样中颗粒的形状与实际的完全相同，现有的技术是做不到的。然而，即使在颗粒形状上存在差异，砂性土在直剪试验中表现的力学特性还是可以被模拟试验准确的再现，以至于追求颗粒形状的完美匹配显得没有必要[7]。

刘清秉等[24]、Ye[25]通过比较样本容量为25、50和100的颗粒的形状统计指标，指出砂性土的某些颗粒形状量化指标受样本容量影响较小。据此，从直剪试验的试样中任意选取了25个砂粒(图2)，基于颗粒的数字图像处理技术[5]，获取颗粒的轮廓后，采用CPA填充技术在PFC中生成目标形状颗粒(图3)。随后按照直剪试验试样的尺寸和级配曲线(图1)生成不规则形状的试样。为进行对比性分析，采用等体积替换法[25]，将不规则的颗粒等体积的替换为圆形颗粒。为方便表述，称圆形颗粒试样为试样一，不规则形状颗粒试样为试样二。由图1可看出替换后试样的级配几乎没变。

图2 电镜下的砂粒Fig.2 Sand under the electron microscope

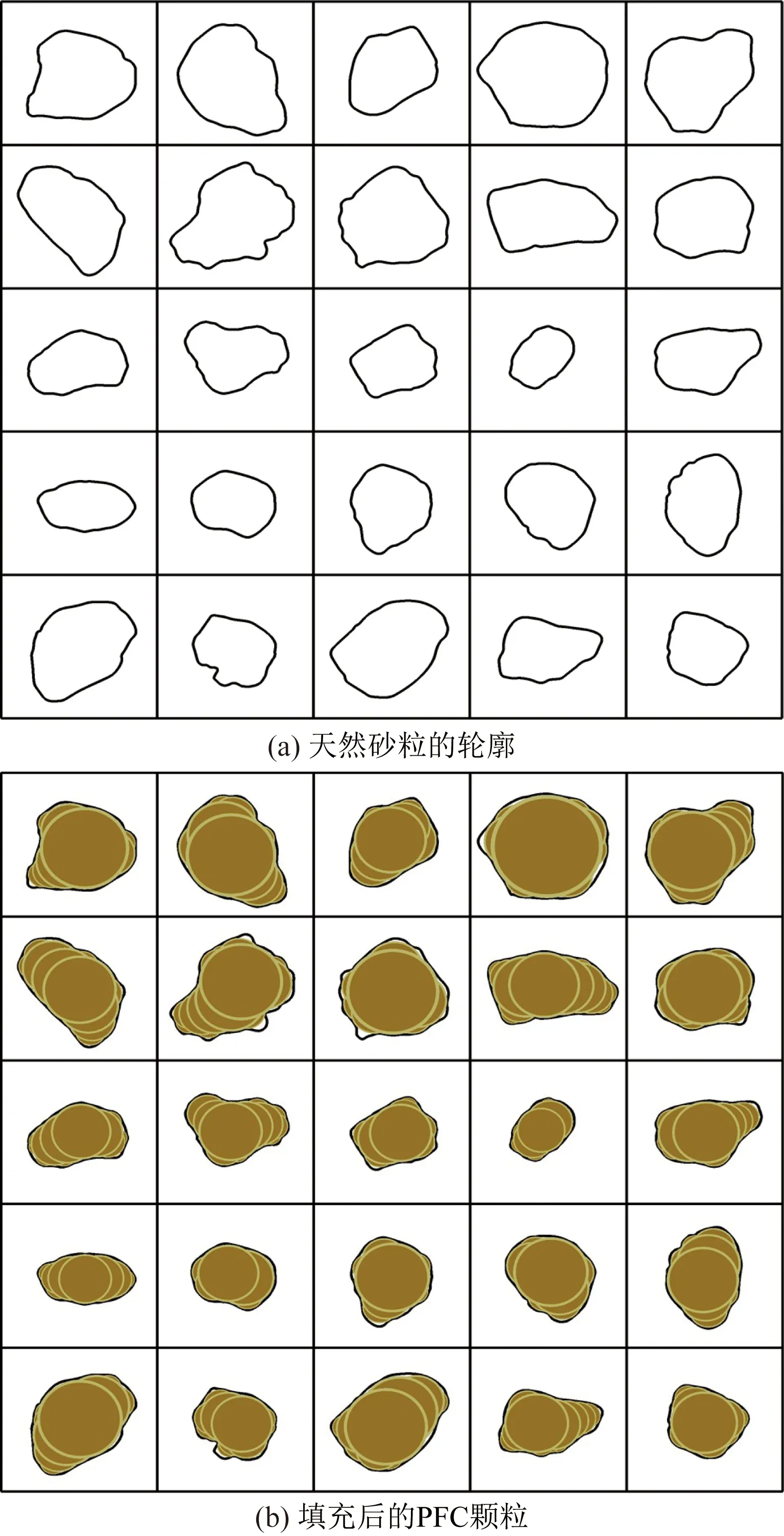
图3 CPA填充技术生成的颗粒Fig.3 Particles generated by CPA filling technology

颗粒在没有摩擦作用时可以堆积成致密的试样，而在较大的摩擦作用时可以堆积成非常松散的试样[26]。在二维模拟试验中必须确定试样的相对密实度，因为颗粒材料的强度和变形性质受砂性土的相对密实度的影响，而颗粒的形状会影响砂性土的极限孔隙比(相对密实度)[2]。通过足够多数量的颗粒即可确定砂性土的极限孔隙率[20]，试样一最小孔隙率为0.098，最大孔隙率为0.188，试样二最小孔隙率为0.076，最大孔隙率为0.142。试样一的极限孔隙比区间长度比试样二的大且试样二最大孔隙比比试样一的小，上述特征符合具有较低的球形度、较高的棱角度和粗糙的表面的砂砾土相比于圆形砂砾土应有较大的极限孔隙比差值的结论[13-14]。基于此，为了与室内试验对应，采用50%的相对密度制成试样以备剪切。

由于试样为硅质砂，且应力水平相对较小(不超过400 kPa)，因此不考虑颗粒破碎对试验结果造成的影响。且认为粒间接触刚度不随接触力的增加而增加，可以采用线性接触模型代替赫兹接触模型。考虑到采用圆形颗粒试样在模拟直剪试验时颗粒的转动应该受到限制，因此，粒间接触模型采用抗旋转的线性接触模型[6]。通过颗粒和接触处设置阻尼以保持剪切过程在准静态的情况下进行。模拟直剪试验采用恒定的剪切速度进行剪切(0.05 mm/s)，至剪位移达到10 mm(剪应变约为16%)时停止。

通过反向拟合室内试验中得到的应力-应变曲线校对模拟试验中的细观参数。考虑到细观参数与砂性土的极限孔隙率的相互影响，反复调试了细观参数，最终细观参数见表1和表2。砂性土的剪切强度或变形会因颗粒空间分布的不同而在一定范围内波动[20]。为此，模拟直剪试验采用3种不同随机数构建模型，分别进行平行试验，取其平均值作为模拟直剪试验的结果并计算其标准差。

表1 接触的细观参数Table 1 Meso-parameters of contact

表2 边界墙和颗粒的细观参数Table 2 Mesoscopic parameters of boundary walls and particles

3 试验结果及讨论

3.1 标定结果

直剪试验及其模拟试验的剪应力-剪位移曲线、法向位移-剪位移曲线见图4和图5(带误差线的均为模拟直剪试验的结果。基于建模方法和细观参数，模拟直剪试验很好地再现了直剪试验的剪切过程。剪切至8～10 mm时，试样的体积基本上处于恒定的状态，即临界状态[17]。通过直剪试验和模拟直剪试验获得的临界摩擦角分别为33.9°和32.3°。基于剪切后的试样所做的6组休止角试验，获得试样休止角为31.8°±0.6°。直剪试验和模拟直剪试验获得的临界摩擦角与试样休止角的平均值分别相差2.1°和0.5°。Herle等[27]曾指出干砂临界摩擦角φcv与其休止角非常接近，相差约±0.5°，并提出了用干砂休止角估算其临界摩擦角的方法。Guo等[16]统计的磨圆度(roundness)较好的渥太华标准砂(Ottawa standard sand)休止角为31°。因此，直剪试验及其模拟直剪试验均具有很好的可信度。

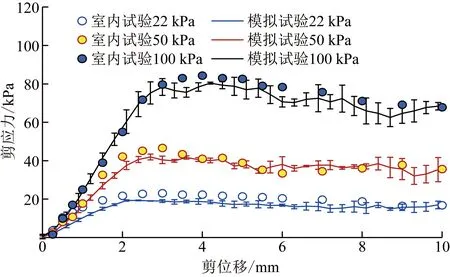
图4 直剪试验及其模拟直剪试验的剪应力-剪位移曲线Fig.4 The shear stress-shear displacement curve of the direct shear test and its simulated direct shear test

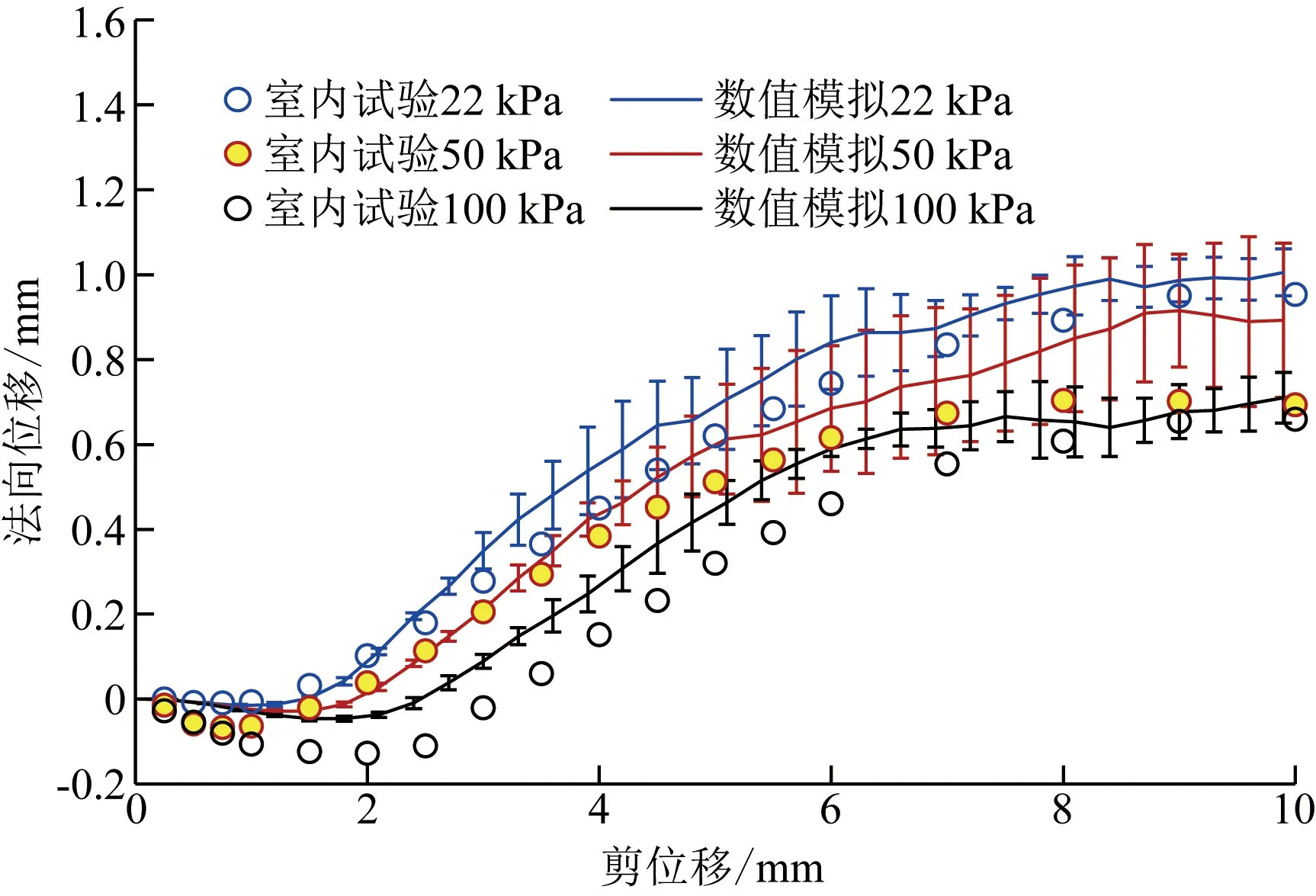
图5 直剪试验及其模拟直剪试验的法向位移-剪位移曲线Fig.5 Normal displacement-shear displacement curve of direct shear test and its simulated direct shear test

3.2 颗粒形状对试样宏观力学性质的影响

试样二与试样一相比，除了颗粒形状上的差别外，试样的相对密实度、颗粒级配、试验条件以及颗粒的数量均是相同的。为了研究法向应力对研究结果的影响，除了采用22、50和100 kPa法向应力外，还增加了法向应力为200、300和400 kPa的模拟直剪试验。两种试样均在极限孔隙率下(密实状态和松散状态)的进行剪切试验。试样密实状态下的峰值强度取剪应力能达到的最大值，临界值强度取8～10 mm段的剪应力平均值并计算其标准差，试样松散状态下的强度取剪应力能达到的最大值。

按照Mohr-Coulomb准则进行直线拟合，得到不同法向应力下密实状态的两种试样的峰值强度和临界值强度(图6和图7)。结果表明，当法向应力小于200 kPa时，试样一峰值强度大于试样二；当法向应力大于200 kPa时，试样一峰值强度小于试样二。随着法向应力增大，试样二表现出较高的剪切强度。试样二临界值强度以及临界摩擦角均略比试样一的大，但差别甚小(试样一和试样二临界摩擦角分别为32.6°和33°)。有文献报道称不规则的颗粒形状会增加砂性土的剪切强度，例如，Kandasami等[4]在300 kPa围压下分别对由石英砂和玻璃球组成的砂性土做了空心圆柱体抗扭试验，得出石英砂不规则的形状增加了试样的剪切强度。然而,Ng[18]在100 kPa围压下基于4种具有不同长细比的椭球体试样进行三轴压缩试验，其结论表明颗粒形状对砂性土的峰值和临界摩擦角影响很小。Cho等[2]表示颗粒形状对砂性土力学特性的影响机理仍不清楚。在颗粒形状影响砂性土极限孔隙比(相对密实度)的情况下，诸多文献忽略了对试样相对密实度的校核[2]，这也是文献[10]中没有注意到的。他们的结论中没有提及颗粒形状对剪切强度大小产生明显影响的条件。模拟直剪试验结果表明，对于密实状态的砂性土，只有在较高的应力水平下颗粒不规则形状才能明显增加砂性土的剪切峰值强度，在较低的法向应力时其剪切峰值强度反而比规则圆形砂性土的低。在文中整个法向应力范围内，试样二临界值强度以及临界摩擦角均略比试样一的大，但差别很小，可以认为颗粒不规则形状没有明显增加砂性土的临界值强度。

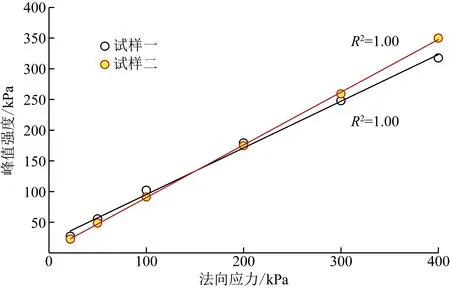
图6 在密实状态下的峰值强度Fig.6 Peak intensity in the dense state

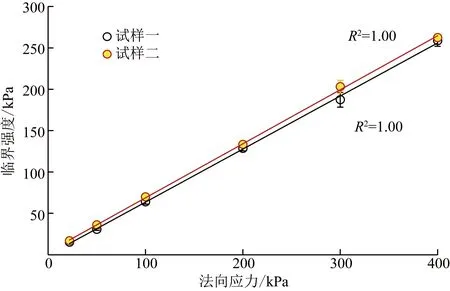
图7 在密实状态下的临界值强度Fig.7 Critical value strength in the dense state

图8为松散状态下的两种试样在不同法向应力时的剪切强度。可以看出，试样二的内摩擦角明显比试样一大，然在较低法向应力时，极值强度上的差别几乎可以忽略，随着法向应力的增加，两种试样极值强度差成比例增加。

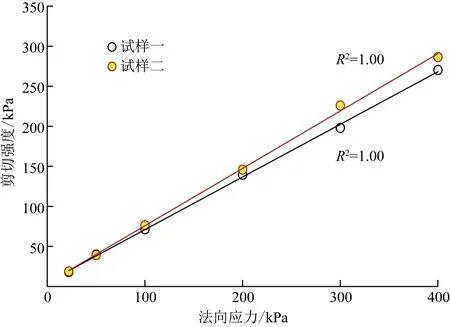
图8 在松散状态下的极值强度Fig.8 The extreme strength in loose state

4 颗粒形状对砂性土力学性质的影响机理

4.1 直剪试验中试样应力的变化

自开始剪切至出现峰值强度的过程中，颗粒间接触力方向由开始的随机分布[图9(a)]转变为定向分布[图9(b)]，即形成柱状力链(column)。当达到峰值强度时，剪切面上柱状力链Fi方向近似相等，令其与法向夹角为θi，则法向应力N、剪应力T与Fi之间的关系式为

(1)

式(1)中：n为剪切面[图9(b)中虚线]上柱状力链的个数。剪切面上n个Fi矢量和可以用一个综合的矢量F表示，其与法向夹角为θ(反算或模拟直剪试验中直接获得)，则法向应力N、剪应力T与F的关系式为

(2)

剪应力T等于0时，θ等于0，意味着没剪切前，剪切面上综合矢量F方向是竖直的。剪应力逐渐增大到峰值过程中，θ亦逐渐增大到极值。一方面，颗粒缓慢移动，在剪切盒对角线方向上颗粒间的接触越来越多，到峰值处最明显；另一方面，对角线方向上颗粒间的接触力逐渐增大，而其他方向上的接触力逐渐向剪切盒对角线方向上偏转、减小或消失 [图9(a)、图9(b)的插图]。剪应力出现峰值后，对角线方向上接触力的增大使其法向分量超过加压板的压力，从而使剪切面以上的颗粒连同加压板反向运动，同时剪切面附近形成的柱状力链绕其中心顺时针转动[22]，θ又开始减小，根据式(1)、式(2)可知，剪应力T亦开始减小，剪切带区域空隙增大，试样体积膨胀。当θi过小时，柱状力链会发生溃曲，新的柱状力链又会生成，剪应力逐渐进入到临界值状态[图9(c)]。

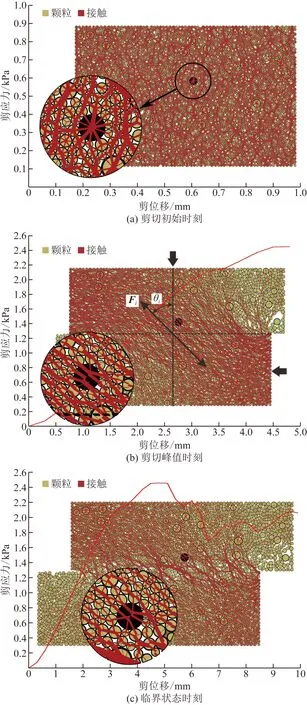
图9 密实试样一剪切过程中不同阶段颗粒间接触力状态(法向应力300 kPa)Fig.9 The state of the contact force between particles at different stages during the shearing process of the compact specimen (normal stress 300 kPa)

根据式(2)中剪应力T、法向应力N和综合矢量F与N夹角θ的关系，提出一种新的本构关系如图10所示，剪应力T的大小可根据参数N和θ做出预测。根据Rowe剪胀理论，等粒径的圆形颗粒极密排列情况下，综合矢量F与法向夹角可达60°，因此0°≤θ≤60°。两种试样表明，剪切过程中θ的变化受颗粒形状的影响，剪应力达到峰值和临界值时的θ分别为θp和θc。

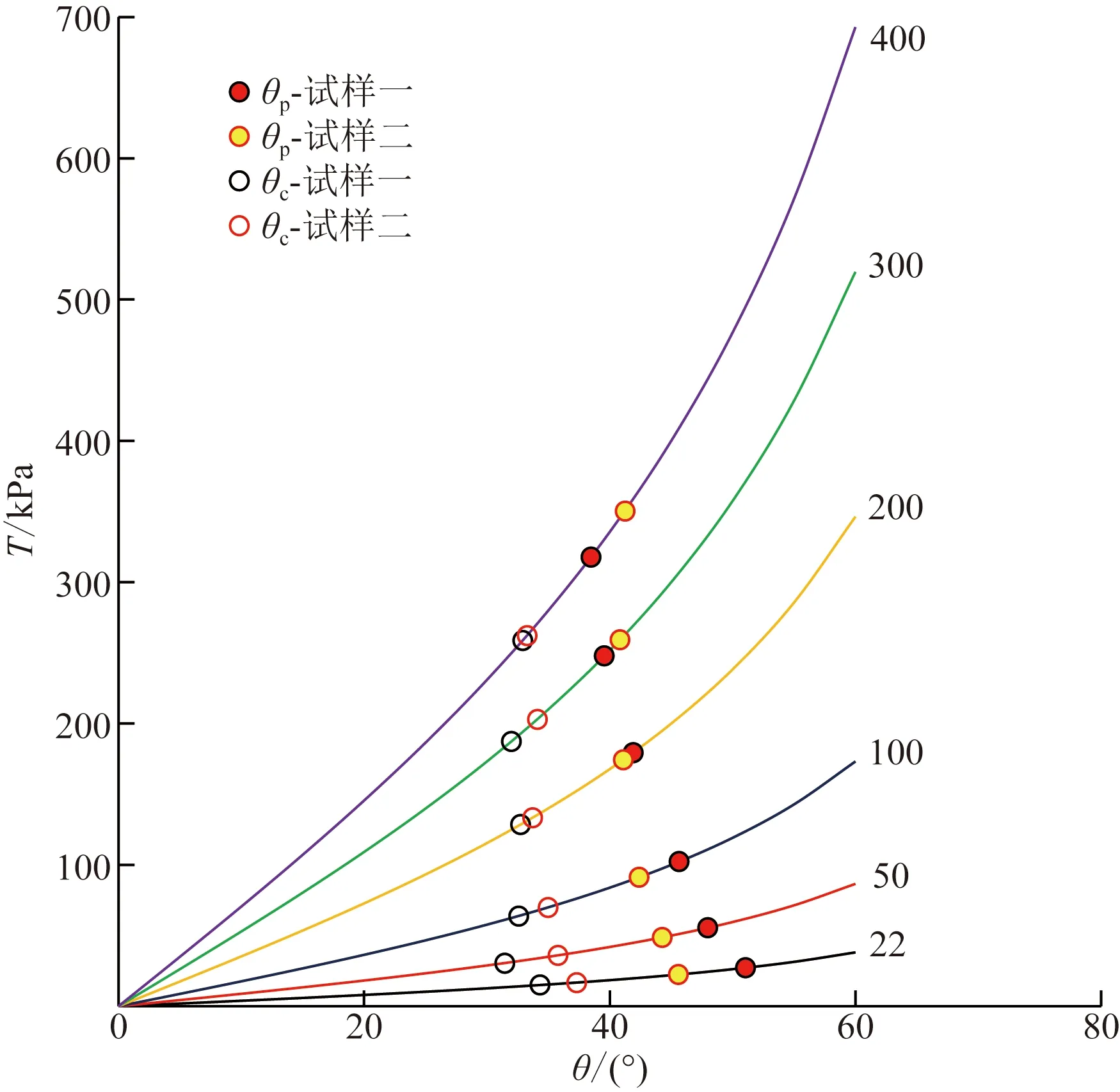
图10 不同法向应力下剪应力T和夹角θ的关系Fig.10 The relationship between the angle θ and the shear stress T under different normal stresses

两种试样的Tp-θp(Tp为峰值剪应力)曲线均较好呈现双曲线形态，低法向应力时，试样一θp偏大而试样二偏小，高应力时相反，θp均落于40°～50°范围，甚至试样二的θp区间更小。而对于Tc-θc(Tc为临界剪应力)曲线而言，试样二依然呈现出较好的双曲线形态，而试样一在低应力时离散性较大，试样二总体上具有较大的θc，且在高应力情况下更明显，θc倾向于30°～40°范围。正如文献[19]中所述，密实试样的θp、θc应介于30°～60°。

4.2 剪胀作用的影响

Rowe[28]认为颗粒间的摩擦作用和剪胀作用是刚性颗粒材料剪切强度的主要来源，提出应力剪胀关系式为

(3)

式(3)中：σ11、σ22为试样所受的最大和最小主应力，Pa；dεv为体积应变增量；dε1为剪切方向上的应变增量；φu为颗粒表面的摩擦因数。式(3)说明，对于同一个试样，其应力比R=σ11/σ22会与剪胀因子D=1-dεv/dε1同步变化，当应力比达到峰值时，剪胀因子会出现最大值。

直剪试验中，有关剪胀角ψ的表达式为

(4)

式(4)中：dεx、dεy分别为试样在剪切方向和法向上的变形增量；tanψ实质上是法向位移-剪位移曲线的斜率。模拟直剪试验结果表明，剪应力峰值所对应的tanψ总是最大的，即最大剪胀角ψmax，不同法向应力下两种试样的ψmax见图11。Bolton[29]在砂土的三轴压缩试验中得出最大剪胀角ψmax与峰值摩擦角φp的关系式为

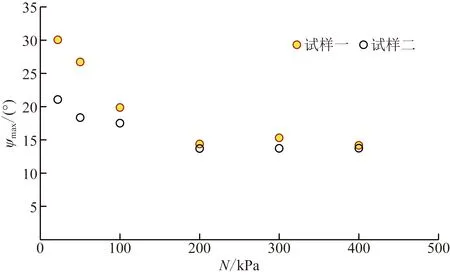
图11 不同法向应力下两种试样的ψmaxFig.11 Two specimens under different normal stresses ψmax

φp=0.8ψmax+φc

(5)

式(5)中：φc为砂土的临界摩擦角。

图12为两种试样的θp、θc与ψmax的关系曲线，虚线为文献[16]基于Ottawa标准砂做的三轴压缩试验中的结果。虽然直剪试验与三轴试验关于参数的定义有所区别，但是它们的物理意义一样，模拟直剪试验结果表明，θp、θc与ψmax同样服从很好的线性关系，与文献[16]的三轴试验结果非常吻合。

当法向应力较小时(22 kPa和50 kPa)，在剪应力达到峰值时，颗粒体尚未出现明显的剪切带，体应变不明显，剪应变很小。根据Barton等[30]提出的不平整的岩体节理面抗剪强度理论，在剪应变较小以及法向应力较小时，剪应力T、法向应力N的关系式为

T=Ntan(θc+ψ)

(6)

由图12可知，在低法向应力时，试样一的峰值剪胀角比试样二的大，而由图7可知，两种试样的θc几乎无差别，因而试样一在低法向应力下峰值强度较大主要原因是试样一的剪胀角比试样二的大些。

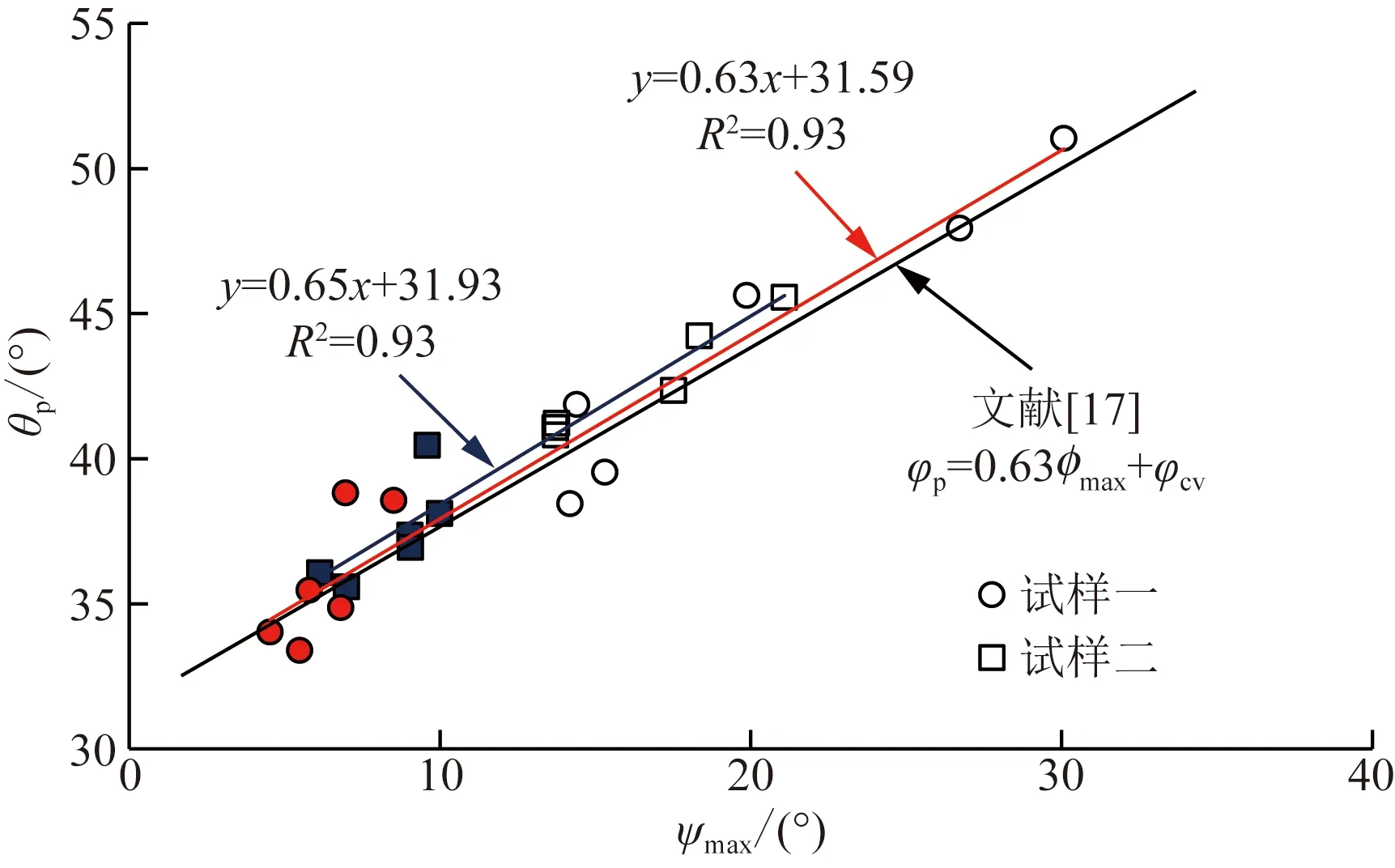
文献[17]公式中，φp和φcv分别为三轴压缩试验中试样的峰值及临界摩擦角，φmax为最大剪胀角图12 两种试样θp、θc与ψmax的关系Fig.12 The relationship between two samples θp，θc and ψmax

图13为圆形颗粒体和椭圆形颗粒体剪胀变形图解，圆形颗粒与椭圆形颗粒的面积相同，假设颗粒间均未发生相对滑动，则柱状颗粒体会发生转动，当发生相同剪切位移时(dεx=1.79)，圆形颗粒体的位移增量(dεy=1.03)要比椭圆形颗粒体的(dεy=0.74)大些，按照剪胀角的定义[式(4)]不难看出圆形试样剪切时具有较大的剪胀角的原因。当法向应力较高(300 kPa和400 kPa)时，剪应力达到峰值时发生了较大的剪切位移，两种试样的峰值剪胀角ψmax也趋于相同，此时式(6)不再适用。文献[17]认为多棱角的颗粒之间可形成锁定(interparticle locking)结构，增加了颗粒体的剪胀性，因而增加了颗粒体的峰值摩擦角φp。

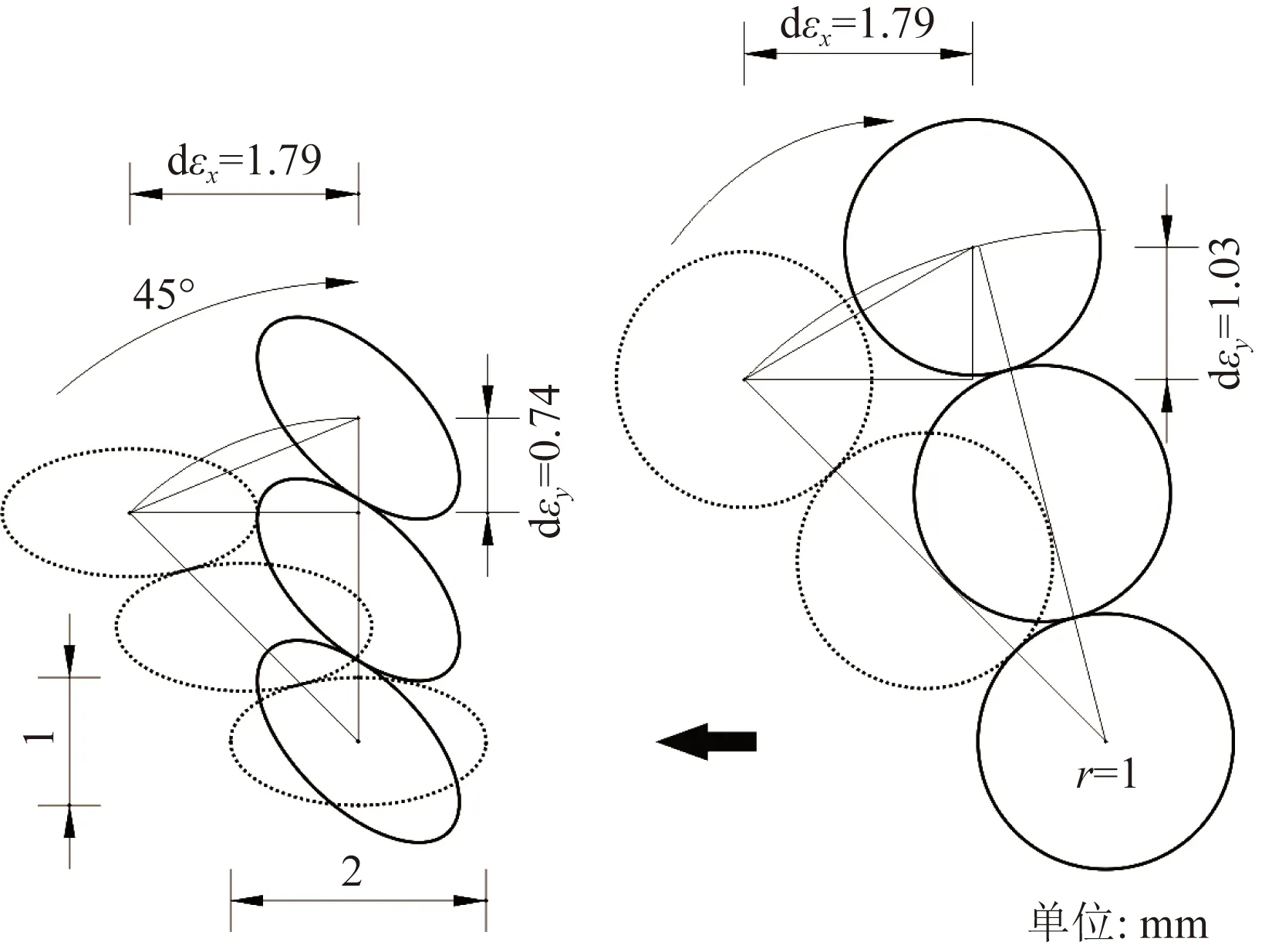
图13 椭圆形与圆形颗粒体变形图解Fig.13 Illustration of deformation of ellipse and round particles

4.3 颗粒间摩擦作用的影响

模拟直剪试验表明，受摩擦作用影响的颗粒间的滑动和滚动及其相互转化机制一定程度上控制着颗粒体的宏观强度，随着颗粒表面摩擦系数的增高，颗粒体的宏观强度呈非比例增高[31]。当抗旋转阻力矩系数小于颗粒表面摩擦因数时，颗粒体强度会因其增大而增大，当抗旋转阻力矩系数超过颗粒表面摩擦因数时，颗粒体强度的增加不再明显[32]。为此，对两种试样在100 kPa法向应力下，颗粒表面摩擦因数在0～1变化时，密实状态颗粒体的强度(峰值强度、临界值强度)进行了探讨，在设定一个颗粒表面摩擦因数时，同时给予一个相同的抗旋转组力矩系数，试验结果见图14。

在没有摩擦的情况下，两种试样的强度值极低，说明摩擦作用是无黏性粗颗粒体(相对于黏土或粉土而言的砂土或粗粒土等)强度的主要来源之一。当摩擦因数为零时，试样一中圆形颗粒间接触力必然通过圆心，这样在没有切向力的情况下，圆形颗粒不受弯矩，因而不会发生转动；相反，试样二颗粒的形状是不规则的，接触力偏离形心，颗粒受到较大的偏心距，所有颗粒均发生较大的转动，导致试样一最终的体积膨胀量(1.77%)远比试样二(0.38%)的大，其强度上的差异可能与此有关。另外，无摩擦作用时，两种试样内颗粒间接触力分布均匀，均无明显的应力局部化现象(即无强弱力链)。

Skinner[33]曾指出临界状态摩擦角几乎不受颗粒间摩擦作用强弱的影响，然而Abriak[34]通过一系列的双轴试验反驳了Skinner的结论，得出当颗粒间摩擦角在0°～30°变化时，相应的临界状态摩擦角从20°增加到26°。模拟直剪试验表明(图14)，两种试样的峰值强度和临界值强度均随着颗粒表面摩擦因数和抗旋转阻力矩系数的升高而非比例升高，这与文献[1]中结论类似。在较低的摩擦作用下，试样二的峰值强度比试样一的低。当颗粒表面摩擦因数较大时，试样二的峰值强度更高，由此可以得出，颗粒间较大的摩擦作用，可使得试样二峰值强度较试样一高。当颗粒间摩擦作用较弱时，临界状态剪切强度受其影响明显，较强时影响不明显。但是，摩擦作用的强弱不会改变不同形状颗粒体临界摩擦角似乎相等这一特征。

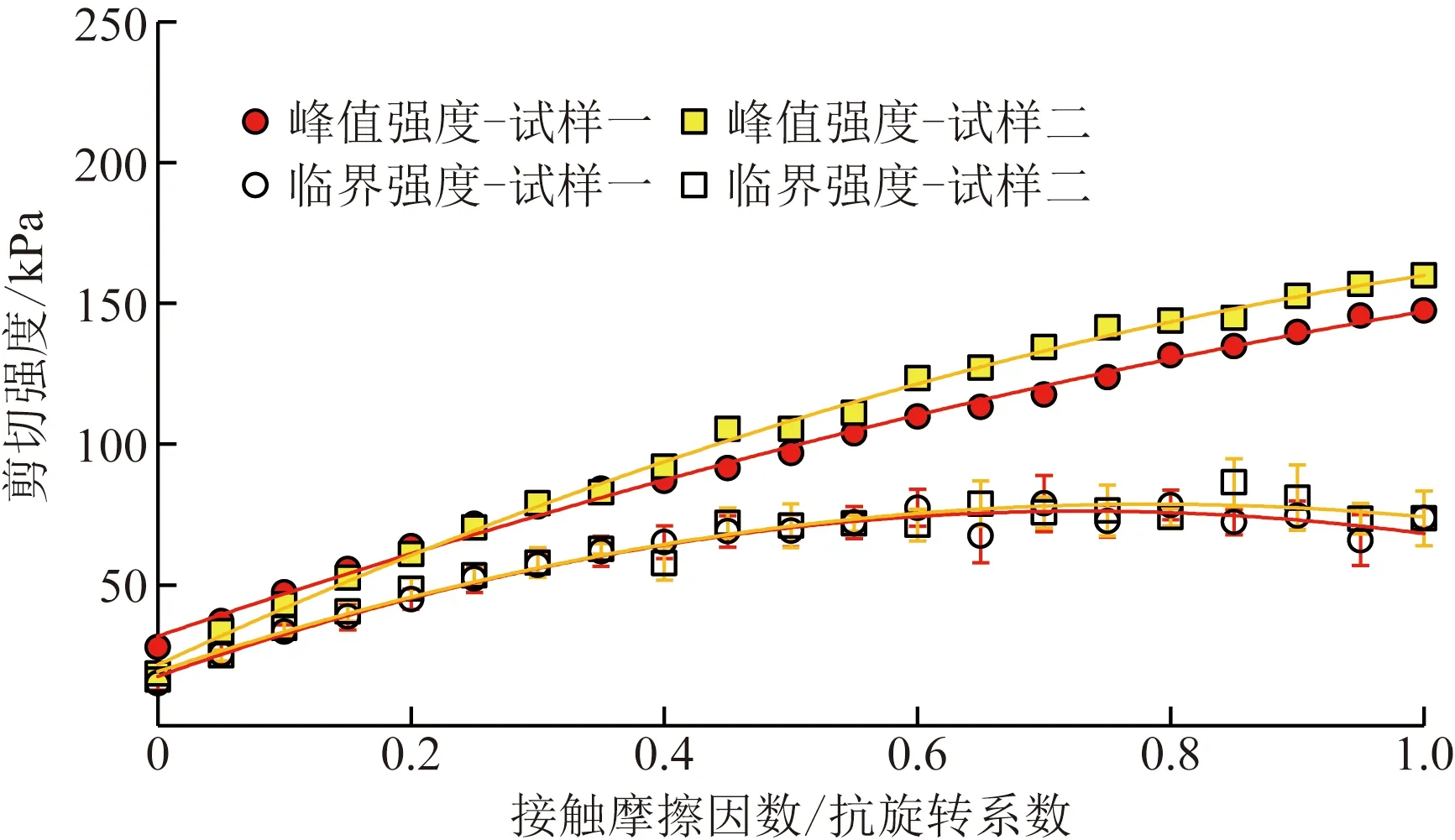
图14 100 kPa法向应力下剪切强度与颗粒表面摩擦因数和抗旋转阻力矩系数比值的关系Fig.14 The relationship between shear strength and the ratio of particle surface friction coefficient and moment coefficient of resistance to rotation at 100 kPa normal stress

5 结论

采用PFC中Clump模块构建不规则形状的颗粒并生成仿真砂样，颗粒的形状取自天然砂粒，一定程度上反映了砂性土中砂粒的形状特征。通过室内直剪试验，标定了模拟直剪试验所需的细观参数，严格地确定了不同试样的极限孔隙率。设定不同的法向应力条件，开展了一系列的模拟直剪试验。通过设置基于圆形颗粒的对比试验，揭示了天然砂性土中颗粒形状对其宏细观力学性质的影响。定义了剪切面上颗粒间接触力合力与法向应力的夹角参数θ，数值上其正切函数值等于剪应力T和法向应力N的比值。基于θ构造了新的本构关系式，揭示了剪应力变化的原因。基于剪胀角理论，从颗粒层面揭示了法向应力较低时不规则形状颗粒体剪切强度较圆形试样低的主要原因。得到如下结论。

(1)密实状态下不规则形状的砂粒组成的试样较圆形颗粒试样具有更大的峰值摩擦角和几乎相等的临界摩擦角；松散状态下具有更大的内摩擦角。

(2)在较低的法向应力条件下密实不规则形状颗粒体的剪切峰值强度比圆形颗粒体低，而在较高的法向应力条件下比圆形颗粒体高。两者临界值强度差别甚小。

(3)法向应力较低时不规则形状颗粒体剪切强度较圆形试样低的主要原因是圆形试样具有较大剪胀角。