基于Moreau包络与迭代重加权策略的图像深度恢复
路 晶
(中国民用航空飞行学院计算机学院,广汉 618307)
深度恢复是计算机视觉的一项基本任务,高质量的深度图为场景重建、飞行自主驾驶等许多计算机视觉任务提供了必要的三维信息[1-2]。虽然高质量的纹理或颜色信息可以很容易地被流行的彩色相机捕获,但对于主流的深度传感器来说,其获得的深度图不可避免地会受到各种退化的影响,如低分辨率、深度缺失或充满噪声等[3]。深度恢复任务的目标是从退化深度测量中恢复高质量的深度图。
深度恢复方法一般包括局部滤波方法和全局优化方法。Tanveer等[4]定义了一个广义滤波器,通过考虑制导图像的内容来计算滤波输出,从而导出一个像双边滤波器的边缘保持平滑算子。王瑞等[5]提出了一种具有简单滤波方法灵活性和速度的边缘感知平滑算法。尽管局部滤波方法简单有效,但短视局部判断通常不能提供足够的信息来捕捉全局结构。相比之下,全局优化方法将深度恢复任务描述为一个包含数据项和正则化项的优化模型。李波等[6]提出了一个马尔可夫随机场(Markov random field,MRF)模型,用于整合低分辨率深度图和高分辨率彩色图。Wang等[7]将正则化项建模为二阶全广义变分正则化,并对非各向异性扩散张量进行加权以指导上采样。交替方向乘子法(alternating direction method of multipliers,ADMM)是一种常用的算法,它通过引入辅助变量和拉格朗日乘子,将原来的复杂优化问题分解为一系列简单的子问题[8]。Yan等[9]提出的增广拉格朗日多重乘子方法通过在目标函数中添加二次罚项和拉格朗日乘子,将约束优化问题替换为一系列无约束问题。尽管取得了上述进展,但仍旧存在几个悬而未决的问题:一是上述方法侧重于寻找深度图的先验知识,但没有充分挖掘深度信号的本质特征;二是凸惩罚函数和非凸惩罚函数都有其固有的缺陷。即凸惩罚函数不足以产生稀疏性。而非凸惩罚函数容易获得局部最优解;三是在实际应用中深度-颜色相关性无法充分得到利用。
为了解决上述问题,现提出一种基于Moreau包络与迭代重加权策略的图像深度恢复方法。基于Moreau包络的非凸惩罚函数能够提高模型的先验稀疏性,同时保持模型的凸性,提出的加速算法能够处理非均匀下采样问题。最后数据集实验结果证明本文方法的有效性。
1 提出的方法
1.1 深度观测模型
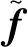
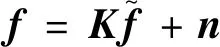
(1)
式(1)中:K为观测矩阵;n为加性高斯白噪声。在不同的情况下,不同的降级可能会作为组合类型出现在捕获的深度图中,并且可以由观测矩阵K表示。
1.2 深度表示模型
根据观察,一般三维场景的深度图主要包含曲线分隔的光滑区域,这种形式的二维数据满足以下情况:在近似分段常数信号重叠时,存在一个相对缓慢变化的多项式信号。随机地从捕获的深度图像中提取一个深度块,并添加方差为25的高斯噪声。分解成分和恢复结果分别用蓝色区域和红色区域表示。深度块可以在强噪声下成功分解为低阶多项式曲面和分段常数分量,揭示了深度图的潜在可分解结构。因此,在每个分量上进行正则化的图像分解模型可以很好地描述此类二维信号。深度观测模型可以描述为
f=K(x+z)+n
(2)

所提出的图像分解模型形式为
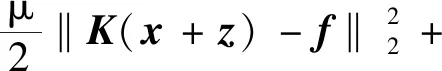
Es(x)+Ep(z)
(3)
式(3)中:等号右侧第一项为数据一致性项,第二项和第三项分别为惩罚x和z的正则化项;标量μ为平衡数据项的相对信度。对分段常数分量x的稀疏惩罚Es定义为
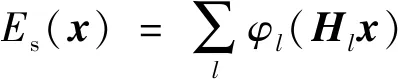
(4)
式(4)中:Hl为由某些滤波算子构成的滤波矩阵;φl:Rn→R为在某些变换中先于约束x的稀疏性的信号域。仅使用稀疏项的惩罚有利于常数解,这使得恢复的深度图像变成一个像卡通图像一样的分段恒定的表面,从而导致某些对象的深度估计不准确。因此,有必要将带有稀疏惩罚的多项式拟合项集成到统一模型中,以解决上述问题。
通常,多项式平滑使用最小二乘法来拟合多项式曲面消除噪声影响,因此,使用它近似于多项式分量表示为
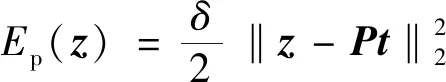
(5)
式(5)中:δ为加权参数;P为预定义的Vandermonde矩阵;t为多项式系数的向量。设z=(z1,z2,…,zN)T是一个N维向量,则

(6)
式(6)中:d为多项式的次数。二阶多项式逼近d=2,足以拟合深度块的多项式分量。
1.3 深度恢复的稀疏性
为提出的模型(3)设计一个正则化项是为了利用非凸惩罚函数来促进先验稀疏性,同时为每个变量保持整个模型的凸性。设D为局部有限差分算子,D=[D1;D2]表示水平和垂直方向上的一阶有限差分算子。提出的稀疏促进先验定义为
Es(x)=ψα(x)=‖Dx‖1-Sα(x)
(7)
式(7)中:Sα(x)为Moreau包络,表达式为
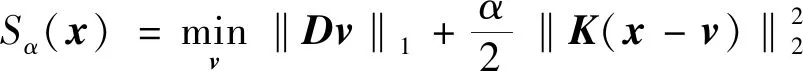
(8)
式(8)中:α为权重参数,α>0。ψα(x)满足以下不等式:
0≤ψα(x)≤‖Dx‖1,∀x
(9)
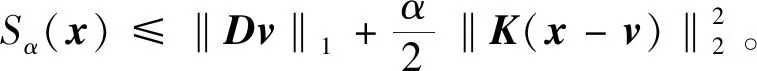
如果将K假定为同一矩阵,则可以将Sα(x)视为变量v的降噪器。一旦获得v,Sα(x)就被转换为一个误差项,该误差项主要包括两个分量,即深度不连续处的大梯度以及x与降噪后的v之间的噪声。当从‖Dx‖1中减去Sα(x)时,ψα(x)仅解决那些梯度误差。在式(6)中排除了大部分深度不连续的梯度,避免了对深度边界的惩罚,间接促进了先验稀疏性。具有稀疏性先验的模型为
(10)
式(10)对于每个变量在条件0 <α≤μ时都是凸的,尽管惩罚函数是非凸的。
命题1(凸性)。令μ>0,α>0,δ>0,多元函数E(x,z):Rn×Rn→R被定义为

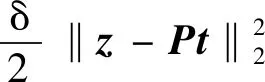
(11)
式(11)中:ψα(x)由式(6)给出。如果0<α≤μ,则E(x,z)分别对于x和z都是凸的。
证明:首先证明E(x,z)对于x是凸的,即
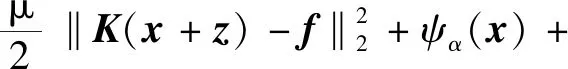
(12)
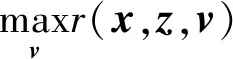
提出的促进稀疏的先验等式[式(6)]被简化为当迭代值为0时的TV-L1。当待估计的基本信号近似分段平滑时,TV-L1是一个合适的工具。TV-L1惩罚的特征表达式为

(13)
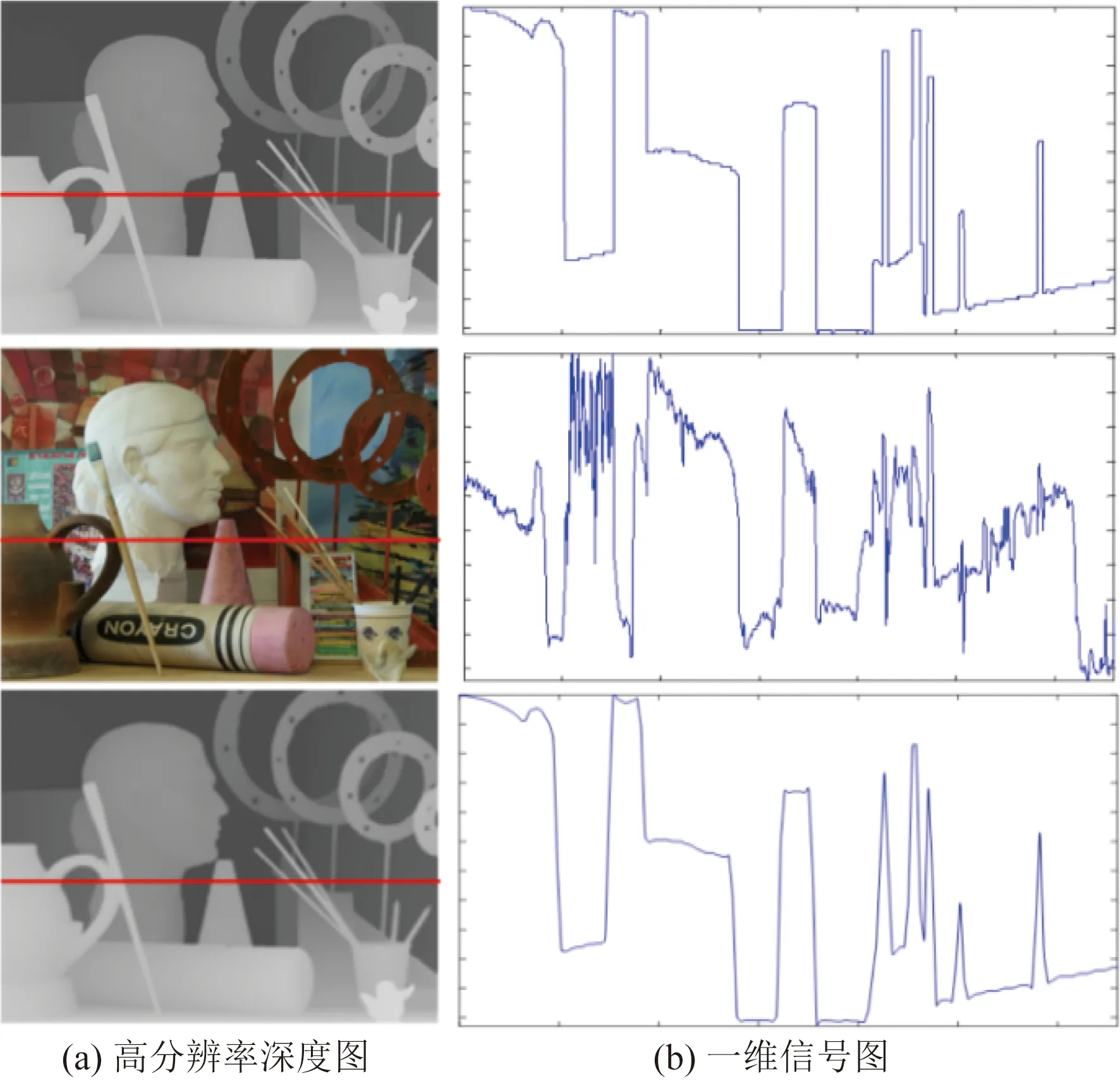
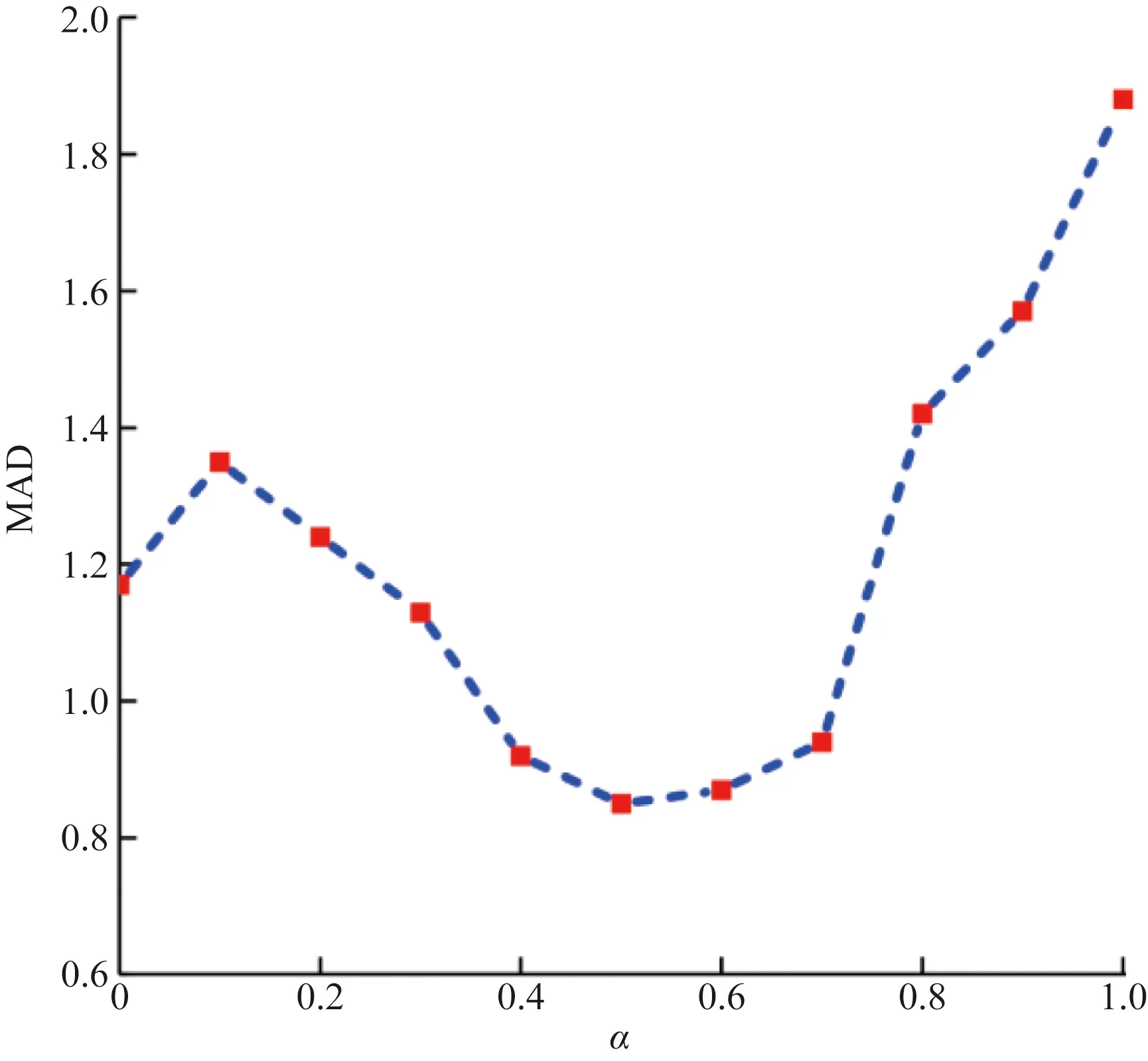
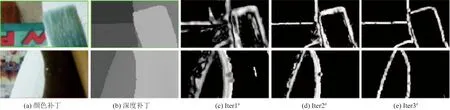
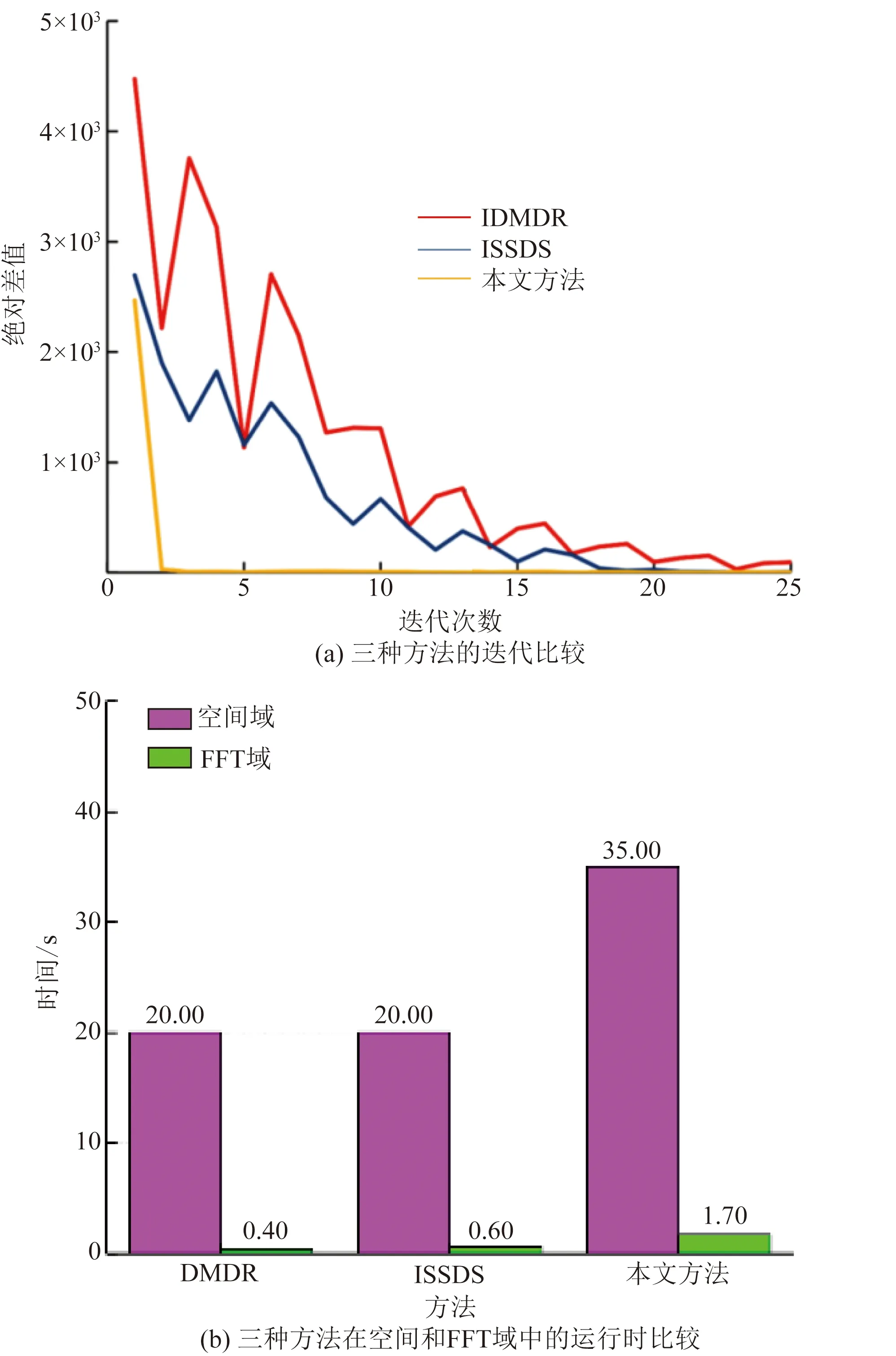
由于分段常数信号的表示是极其稀疏的,因此与非凸惩罚(TV-Lp)相比,L1范数通常不足以产生稀疏性(0 (14) 式(14)中:0 深度图包含由深度边缘分隔开的平滑区域,真正影响深度质量的是深度边缘的清晰度,好的边缘保留技术通常可以保证恢复性能。图1(a)从上至下分别显示了高分辨率深度图,高质量彩色图像和低分辨率深度图深度。通过在图1(b)中绘制一维信号可以看出,深度图中的边缘在彩色图像中具有对应的位置,因此可以从随附的彩色图像中推断出深度图中的边缘位置。但是,并非总是如此,因为表面纹理的强度变化与深度无关。通过检查局部纹理和深度层边界之间的一致性来制定重加权的相似性度量ω来定位深度边界并处理不一致的问题,其计算如下。 图1 颜色和深度信息之间相互关系的图示Fig.1 An illustration of the relationship between color and depth information ω[fk(p),fc(p)]= (15) 式(15)中:fk和fc分别为从第k次迭代获得的深度图和彩色图像;g[fk(p)]={‖D1fk‖p′,[|D2fk|]p′}、p′∈N(p)为每个像素p的局部邻域N(p)内的水平方向和垂直方向梯度的拼接;g[fc(p)]为彩色图像上梯度的拼接;<·和·>为点积运算。 然后,可以简单地将其相似性度量ω集成到式(6)中的惩罚项中,可得 ψα(x)=‖ω○Dx‖1-Sα(x) (16) 式(16)中:○为逐元素乘法。ω可以校正梯度,并减少对出现在深度边界处的有意义差异的损失,这可被视为促进稀疏性的一种方式。 引入近端梯度方法来求解基于稀疏促进先验的模型,即 F(x)=h1(x)+h2(x) (17) 式(17)中:h1:Rn→R和h2:Rn→R∪(+∞)都是闭合的正凸,而h1是可微的。近端梯度法具有以下迭代方案,表达式为 (18) (19) 式中:ζ为辅助变量;π为步长。根据在式(9)中提出的模型,则 (20) (21) h1的梯度等价于 (22) (23) (24) (25) (26) 算法11:输入:观测深度图f0,观测矩阵K,范德蒙矩阵(二阶)P,差矩阵D,推断相似度w;α>0,μ>0,δ=1,k=0。2:while不收敛的情况下do。3:通过使用式(7)最小化x~。4:通过式(22)、式(24)、式(25)和式(13)计算x~、xkm、fkm和ωk。5:通过执行ADMM算法来最小化式(26)。6:k=k+1。7:endwhile。8:输出:f=xk+1+Ptk+1。 定理(收敛分析):令h1:Rn→R和h2:Rn→R∪(+∞)都是闭合的适当凸函数,并且h1是可微的。假设h1+h2的最优解集X*是非空的,令{xk}是由式(10)使用近端梯度法生成的序列,并假设如果给出xk,则zk和tk也已知。然后 (27) 此外,{xk}收敛到x*∈X*,并且对于所有k=0,1,…有 (28) 式(28)中:l(x;xk)为h1(x)在xk处的线性近似,表示为 (29) 基于ADMM算法的加速算法,最小化式(23)。需要引入一个辅助变量y,并利用ADMM算法形成一个不受约束的模型,即 Lβ(x,y,z,t,λ)=‖ωk○y‖1+〈λ,Dx-y〉+ (30) 式(30)中:λ为矢量形式的拉格朗日乘数;β为惩罚参数。对于x子问题,封闭式解决方案为 (31) 通常,为了加速计算,采用快速傅立叶变换(fast Fourier transform,FFT)技术将问题变换到FFT域。但是,FFT不能直接用于解决x子问题,除了KTK是相同的矩阵,即整个模型降级为去噪问题。在此方案中,观察矩阵K是用于超分辨率任务的下采样矩阵,或者是用于图像修复的指示矩阵。分母βjDTD+μjKTK通过FFT技术既不是对角线也不能对角线化。为解决这个问题,在原始问题式(26)中引入了一个新的辅助变量u,从而转换为以下优化问题,即 (32) 相应的增强拉格朗日函数修改为 Lβ1,β2(x,u,y,z,t,λ1,λ2)=‖ωk○y‖1+ 〈λ1,Dx-y〉+〈λ2,x-u〉+ (33) 式(33)中:λ1、λ2为矩阵中与x大小相同的拉格朗日乘数;β1、β2为惩罚参数。然后,可以通过ADMM算法将原始x子问题分为两个问题。 x子问题公式为 (34) u子问题公式为 (35) 式中:F(·)、F-1(·)分别为离散傅里叶变换(discrete Fourier transform,DFT)及其逆变换;I为相同的矩阵。 所有其余的z、y和t的子问题都具有近似形式的解决方案,并且可以低复杂度解决。如算法2所示,其中soft(·)表示软阈值函数。z子问题的公式与u子问题相似,也可以通过按元素划分来解决。 算法2加速算法1:输入:观测深度块fkm,观测矩阵K,范德蒙德矩阵P,差分矩阵D,从彩色图像推断出的加权矢量w,x0=K-1fkm,x0=u0=z0,λ01=0,λ02=0,β01>0,β02>0,μ0>0,δ=1。固定步距ρ0≥1,ρ1>1,ρ2>1,j=0。2:while在未收敛do。3:yj+1=soft[wk○(Dxj+λj1/βj1),wk/βj1]4:通过式(30)、式(31)分别计算xj+1、uj+1。5:zj+1=(μjKTK+δI)-1[μjKT(fkm≤-Kxj+1)+δPtj]6:tj+1=P+zj+1。7:λj+11=λj1-βj1(yj+1-Dxj+1)。8:λj+12=λj2-βj2(uj+1-xj+1)。9:μj+1=ρ0μj,βj+11=ρ1βj1,βj+12=ρ2βj2。10:j=j+1。11:endwhile。12:输出:xk+1,zk+1,tk+1。 数据集是基于Middleburry数据集合成的,该数据集具有3种典型的深度降级模式,即下采样降级(2×、4×、8×和16×),降级和类似Kinect的退化。测试图像包括6个深度颜色对,即来自Middleburry数据集的Art、Book、Dolls、Laundry、Moebius和Reindeer。 (1)参数设置。根据噪声量对μ进行调谐,对于下采样和Kinect类降级,分别设置μ=1,对于ToF类降级分别设置μ=0.1。对于TV-L1和TV-Lp来说,β、ρ0和ρ1分别设置为0.005、1.5和1.25。对于TV-Lp来说,ρ设置为0.85。为加速算法设置了β1=0.004,β2=0.002,ρ0=1,ρ1=1.25,ρ2=1.25。平均绝对误差(mean absolute deviation,MAD)用于测量恢复的深度图及其对应的地面真实值之间的差。所有实验均以简单的MATLAB代码实施,并在具有Intel(R)Core(TM)3.4-GHz i7 CPU和8.0 GB RAM的台式机上运行。 (2)对比方法。通过将高斯加权扩展到交叉双边加权的改进马尔科夫损失选择(Markov loss selective,MLS)方案,被称为改进的MLS(improved Markov loss selective,IMLS)[10]。像素引导的局部模型滤波(color-guided local model filtering,CLMF)方法有两种版本:分别为零阶和一阶多项式模型的CLMF0和CLMF1[11]。当式(6)中α=0时,深度模型的分解恢复(depth model decomposition recovering,DMDR)与具有稀疏性先于模型的模型相似,但没有引入重加权策略[12]。结构选择深度超分辨(structure selective depth superresolution,SSDS)与之前使用TV-Lp的模型相似,但是没有多项式项和重加权策略[13]。因此,通过添加相应的组件来改进这两种方法,并将它们分别重命名为改进的DMDR (IDMDR)和改进的SSDS(ISSDS)[14],除此之外,还包括传统图像恢复方法:Guided[4],Bicubic[5],Edge[6],JBU[6],FGI[7],TGV[8],FBS[9]。 表1表明,在4种不同的上采样因子中,该方法在MAD中取得了较好的实验结果。与IMAMRF[15]相比,提出的方法在大多数情况下均能达到最佳性能,并且在大多数情况下明显超过了IMJBU[15],IMMRF[16],PRE[16]和IR-WLS[17]。 表1 2×、4×、8×、16×下降采样降解下的定量比较结果Table 1 Quantitative comparison results under degradation of 2×,4×,8×,16×descending sampling 图2给出了Laundry的8×深度采样深度图和残差图的结果。IMLS、CLMF、Guided和FBS倾向于平滑深度图的边缘。FGI 也模糊了窗口,无法恢复椅子后面的深度值。TGV具有严重的纹理复制伪影。AR和IR-WLS显示了良好的性能,但仍然不如本文方法,特别是在图像的边缘。本文方法可以保留深度边界并提供视觉上更加一致的结果,而不会出现伪图像。 图2 8×下采样降级的深度恢复结果Fig.2 Depth restoration results of 8× down sampling degradation 通过向原始数据集中添加方差为25的高斯噪声并以不同的下采样速率对污染的数据集进行下采样来模拟ToF样的深度下降,表2显示了与其他方法的定量对比结果。 表2 类ToF的定量对比结果Table 2 Quantitative comparison results of type ToF 本文方法在2×和4×上采样方面优于所有方法。对于8×和16×上采样,其结果略逊于FGI和FBS,因为这两种方法主要旨在设计严重噪声情况下的插值技术,而本文方法适用于各种降级,因此总体来看,本文方法具有更好的泛化性能,是一种通用的深度恢复方法。 图3显示了Reindeer对类似ToF的降解情况的结果,Bicubic和Guided 在处理类似ToF的降解时无效。JGF[8]、IMLS和CLMF0的降噪性能较差。本文方法的去噪性能相比于其他方法已得到明显改善。此外,尽管结果在8×上采样的定量比较中具有较低的度量值,但视觉比较显示了该方法的优越性。从残差图可知,在大多数深度边界上都比其他方法获得了更好的恢复性能,但是本文方法的结果受到一些值较大的离群值影响。 进一步测试了类似Kinect的退化下的性能,如表3所示。在这种情况下,结构缺失会随着深度不连续而产生,而平坦区域会产生随机缺失。采用类似Kinect的退化图像作为测试图像,这些图像缺少大多数深度边界,增加了定位深度不连续性的难度。 表3 在类Kinect的降解下的定量比较结果Table 3 Quantitative comparison results under Kinect like degradation 从表3可以看出,所提方法在所有情况下都能达到最低的MAD值,并且在很大程度上优于现有的方法,这说明了本文方法在处理类Kinect退化时的有效性。直观比较如图4所示,结果表明,对于平面区域的随机缺失和缺失区域内的急剧不连续具有最佳的恢复效果。 图4 类似Kinect的深度恢复结果Fig.4 Depth restoration results similar to Kinect (1)稀疏先验。为了进行比较,在IDMDR和ISSDS模型中都保持多项式项和重加权策略不变,并测试了惩罚函数对稀疏先验的影响。IDMDR、ISSDR和稀疏先验之间的客观和视觉比较可在上述3种情况下对所有3种类型的降解进行了比较。所有实验均证明,本文方法在所有任务上均比IDMDR和ISSDS取得更好的结果。 (2)Moreau中的参数α。加权参数α在Moreau增强惩罚中起重要作用。对于固定变量μ=1,在0≤α≤μ的条件下,每个变量的整个模型都是凸的。如果α=0,则将提出的模型简化为具有L1范数的基本模型(即IDMDR)。图5还给出了相应的视觉结果,当α<0.5时,出现点状伪影。相反,当α接近1时,恢复的深度图十分模糊,当α接近0.5时,可获得最佳视觉效果。图6显示了在不同的α下,Dolls的ToF类降解性能。当α=0.5时,MAD最低。 图5 参数α对4×下采样率的ToF样衰减的影响Fig.5 Effect of parameters αon ToF sample attenuation at 4× down sampling rate 图6 参数α在提出模型中的影响Fig.6 Influence of parameters α in the proposed model (3)重加权策略。列出有或没有加权策略的恢复结果,以研究其对模型的影响。图7中最上面一行表示无重加权方案恢复策略,而在最下面一行表示具有重加权方案的恢复策略。图7中的视觉比较和客观MAD值表明,重加权策略对这3种方法都有提升效果。一旦将深度信息中断整合到模型中,就可以提供深度边界的位置,这有助于模型保留深度边缘。此外,通过图8中的重加权策略显示了每次迭代的推断深度边缘。随着迭代的进行,预测的深度边界更加清晰和准确,从而可以帮助模型定位深度不连续之处。 图7 重新加权方案对8×下降采样退化的影响Fig.7 Effect of reweighting scheme on 8× down sampling degradation 图8 重加权方案的深度边缘Fig.8 Depth edge of reweighting scheme (4)多项式项。多项式平滑项旨在将深度变化的表面分量拟合到深度图中。通过从完整模型中删除它来测试其有效性。图9显示了在具有和不具有多项式拟合项的模型之间比较的恢复结果。没有多项式项的情况会产生严重的阶梯假象,这表明仅稀疏先验不足以适合潜在深度信号。相反,所提出的具有多项式拟合的模型可以更好地描绘2D深度信号,特别是对于缓慢变化的表面。 图10(a)所示为此算法的收敛行为。以Dolls的ToF样降级(8×下采样)为例,绘制了两个连续的恢复深度图之间的绝对差。提出算法迅速减小了差值并收敛到固定点,且差异单调减少,并且3~5次迭代足以获得较好的结果。为了进一步比较,还绘制了IDMDR和ISSDS的收敛曲线。与本文方法相比,IDMDR和ISSDS的曲线波动较大,并且会收敛迭代次数大约为20次。进一步证明了本文方法的收敛性能较好。 图10 性能对比Fig.10 Performance comparison 为了评估加速算法的运行时间,分别在空间和频域上执行原始算法和FFT加速算法。此比较使用8×下采样降级的情况(LR深度图像为165×135,HR强度图像为1 320×1 080)。由于IDMDR和ISSDS与数据观测项相同,因此在这两种方法中也采用了加速算法来进一步验证加速算法。比较结果显示于图10(b)。对于此模型,空间求解器需要大约35 s的时间,这在计算上是非常苛刻的。本文算法仅需1.7 s即可解决优化问题。从其他两种方法可以得出类似的结论。请注意,尽管此模型的迭代次数为3~5,但比IDMDR和ISSDS花费的时间要少得多。这是因为此算法包含用于解决整个模型的外部迭代k和用于解决子问题的内部迭代j。内部迭代需要15~20次迭代才能获得局部最优解。 为了解决现有的深度恢复方法存在的局限性,提出了一种基于Moreau包络与迭代重加权策略的图像深度恢复方法。通过多个数据集实验证明了如下结论。 (1)本文方法能够有效提升图像恢复效果,可以保留深度边界而不会出现伪图像,并且运行时间具有一定的优势。 (2)本文方法适用于各种降级,具有更好的泛化性能,是一种通用的深度恢复方法。 (3)重加权策略有助于模型保留深度边缘,而提出的具有多项式拟合模型可以更好地描绘2D深度信号。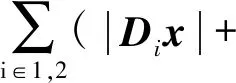
1.4 重加权策略

2 算法
2.1 该模型的算法
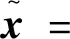

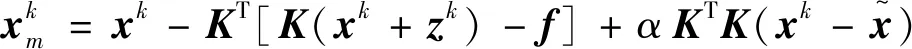
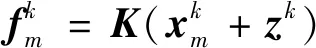
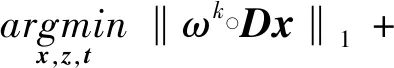

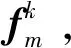

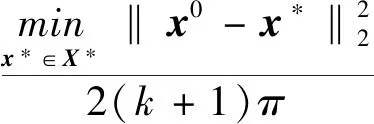
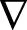
2.2 加速算法
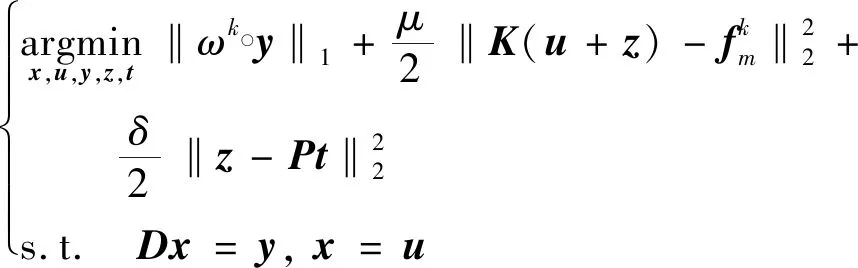

3 实验和结果
3.1 实验环境
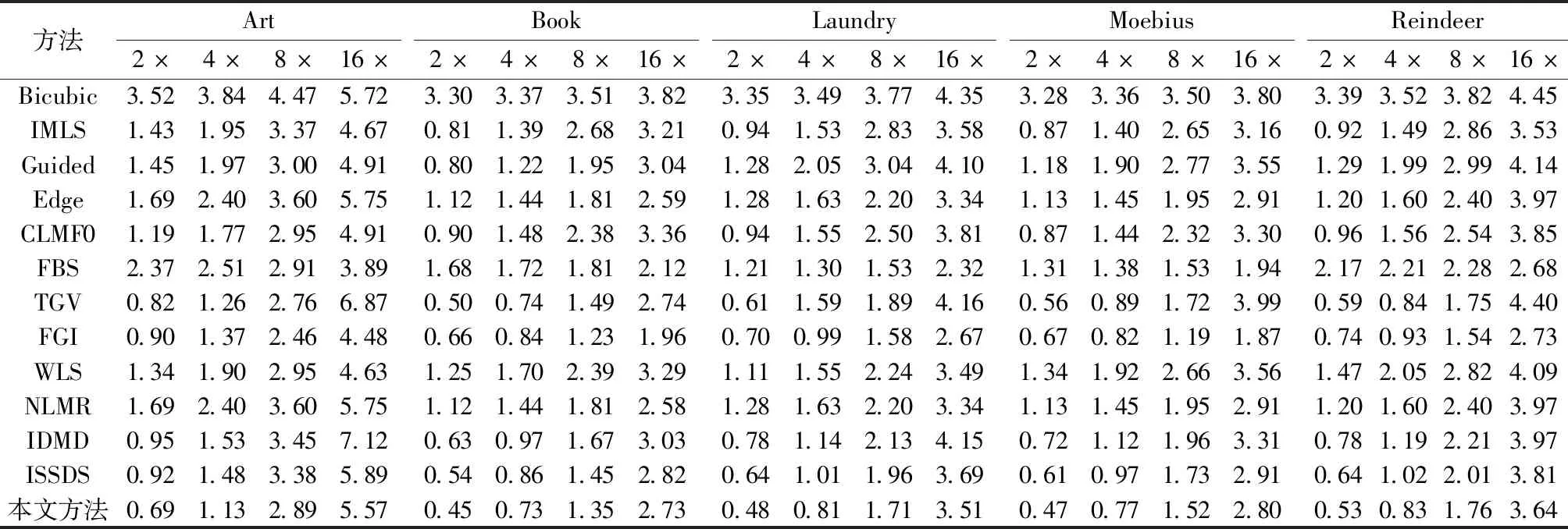
3.2 下采样降级的实验
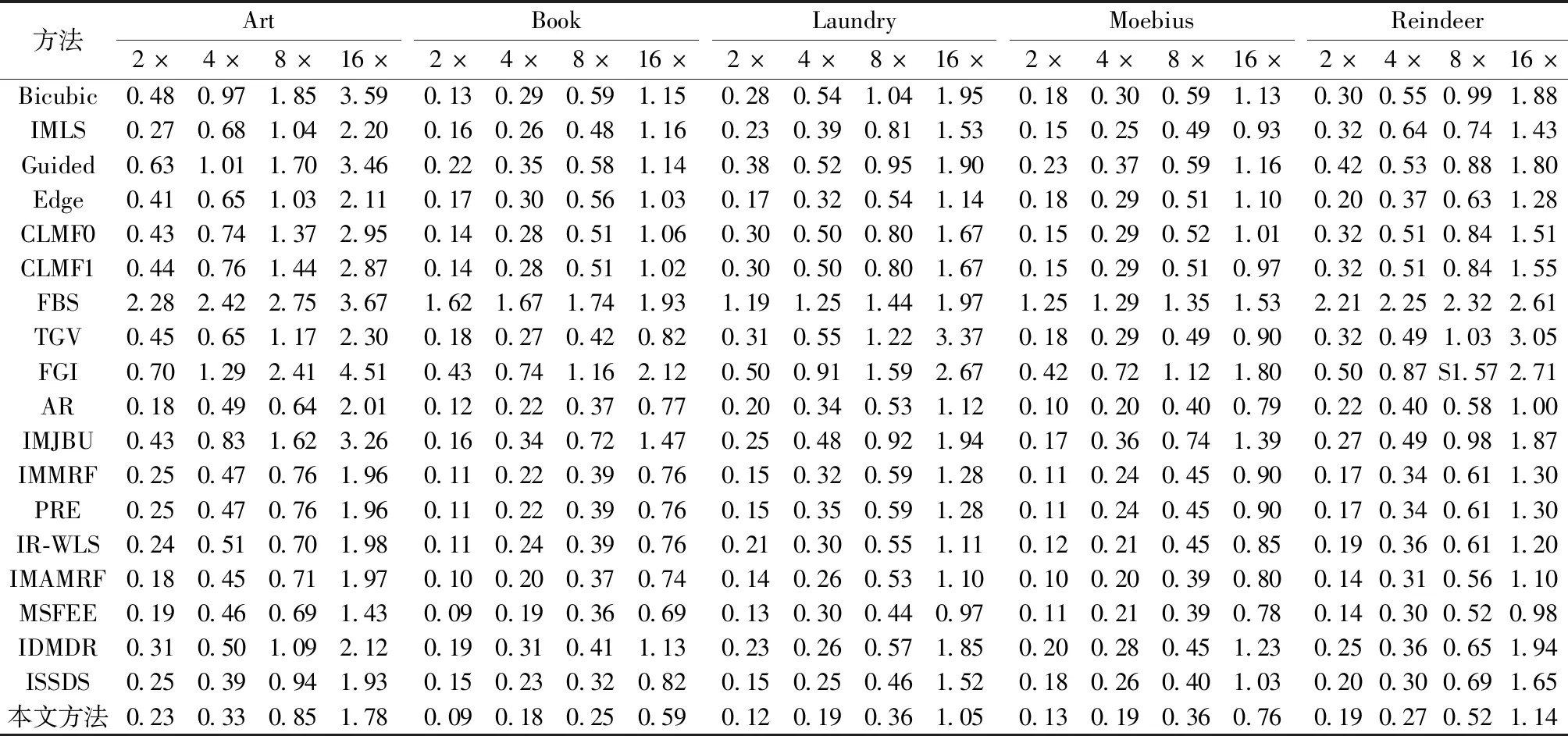
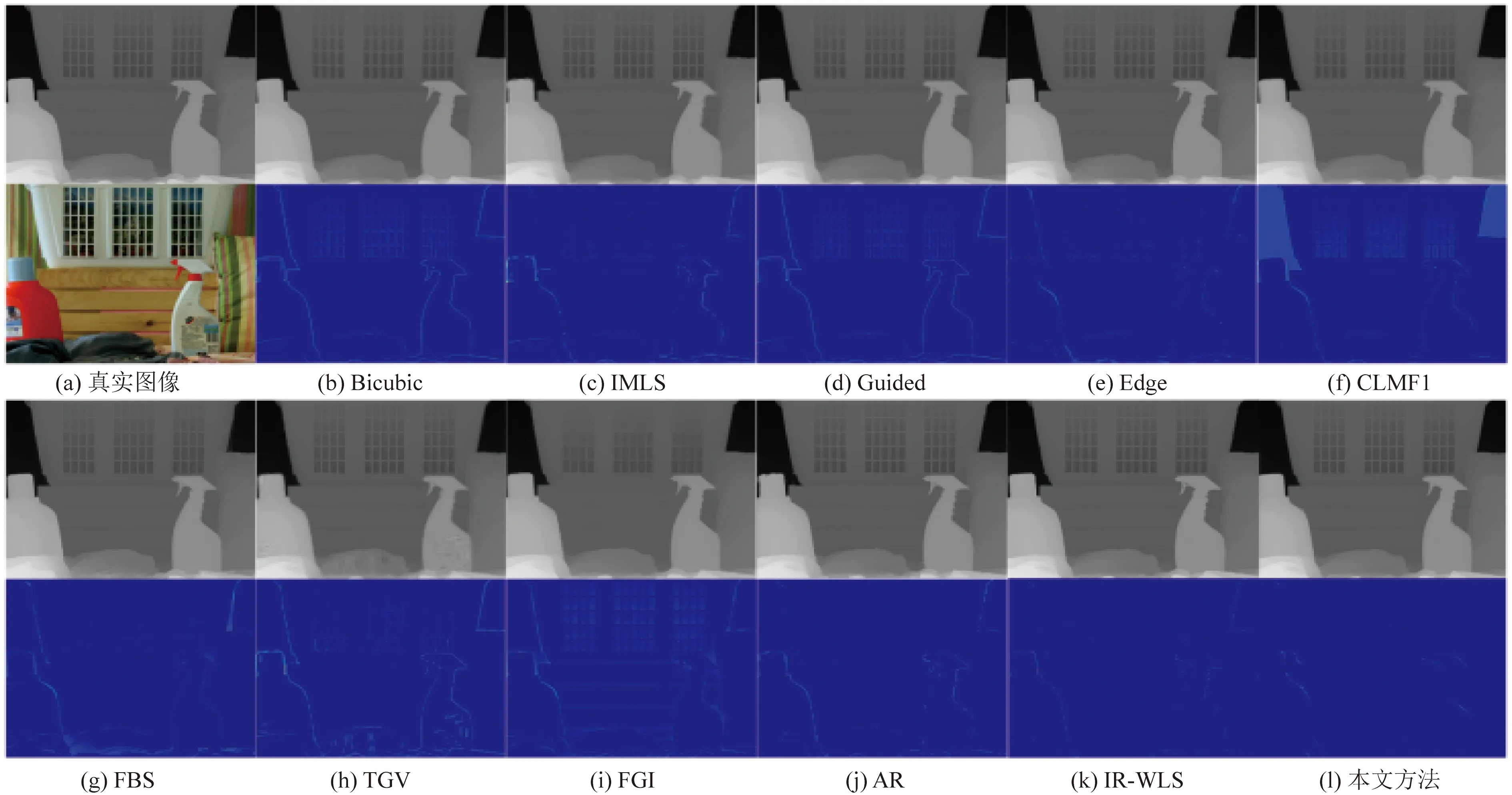
3.3 类ToF的降解实验
3.4 类Kinect降解实验
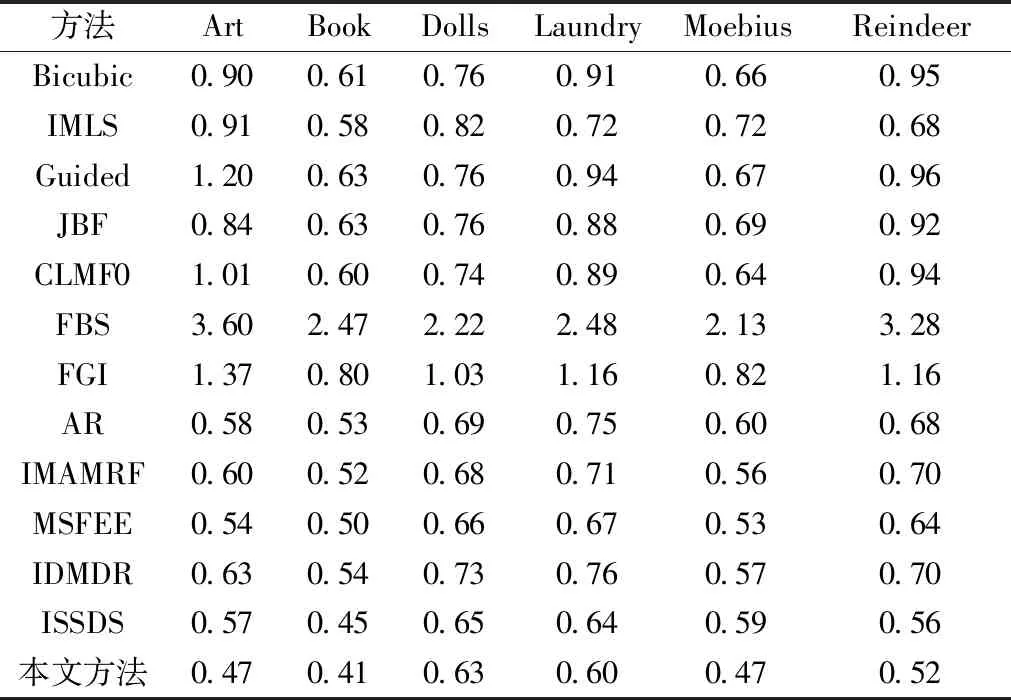

3.5 消融研究


3.6 收敛性和运行时间
4 结论

