高速公路路堑风雪流灾害预测模型与应用
陈彦欣,樊宏宇,常江芳,李志达,刘明国,钱家珺
(1.河北省高速公路延崇筹建处,石家庄 075400;2.中交远洲交通科技集团有限公司,石家庄 050043;3.石家庄铁道大学工程力学系,石家庄 050043;4.河北省金属矿山安全高效开采技术创新中心,石家庄 050043)
风雪流(也称风吹雪)是指在一定风速下雪颗粒随风运动迁移并沉积的现象。宽阔平坦的地区风雪流不会对道路造成太大影响,但是对于地形复杂的山区,山体轮廓会使风速及风向发生改变,常常致使高速公路因严重积雪而阻断交通。特别是当路基断面为路堑形式时,灾害情况尤其严重。引起雪颗粒迁移沉积的重要因素是风,因此对路堑周围流场时空分布规律的研究是把握风雪流致灾机理的关键。
对风的流场的研究,除了现场观测和室内风洞试验外[1-4],数值模拟是最为便捷有效的方法[5-8]。大量学者对路堑形式下公路风雪流进行了研究,如庄小清等[9]对全路堑风速场进行了数值模拟,揭示了全路堑边坡坡度、深度对风雪流的影响规律;周晓鸥等[10]研究了公路路堑风雪流的发生条件及风速、路基形式等对风雪流的影响;苏国平[11]比较了净风和风雪两相流两种模式对铁路路堑流场的影响。周开方[12]对背风半路堑风速场进行了定量研究。然而,目前这些研究多未考虑周围地形(如山体)对风雪流的影响。事实上山体对风血流的流场分布规律有重要影响,因此,在考虑风雪流的主要影响因素时,除了风、雪与路基形式外,还考虑包括周围山体地形的影响。
现针对多种路堑形式,考虑周围山体、路堑深度、路堑边坡坡度、路堑与山体相对位置及风速等多重因素,利用Fluent数值模拟软件展开回归正交试验,分析各因素的影响程度,建立风雪流灾害预测模型。最后,结合延崇高速公路典型地段对预测模型进行验证,旨在为高速公路路堑积雪的预测提供便捷途径,为风雪流灾害的防控提供理论依据。
1 数值试验
1.1 回归正交试验设计
回归正交试验通过有机结合回归分析法和正交实验法,实现较少试验次数情况下获得更高精度的回归方程,是常用的考虑多因素影响的试验设计方法。采用回归正交试验方法设计数值模拟方案。
(1)确定目标函数。以公路横截面中路面上方风速小于雪颗粒启动风速的分布面积作为目标函数。雪颗粒粒径范围一般为2~5 mm,根据王中隆等[13]提出的启动风速Vt分别与雪颗粒粒径D和积雪密度ρs之间的关系[式(1)和式(2)],可知启动风速在5.5~6.7 m/s,考虑到山体地形的影响,风速取为6.7 m/s,风速小于该值则雪颗粒出现沉降。

(1)
Vt=3.123+11.99ρs+0.135e12gρs
(2)
(2)确定因素及水平。选取10 m高度处风速v0、路基与山体横向距离L、路堑深度h、路堑坡度α及山体相对高度H共5个关键因素,全路堑、迎风半路堑和背风半路堑的示意图如图1所示。对各因素水平进行编码,并确定其取值:以Z1j和Z2j分别表示因素Zj(j=1,2,3,4,5)的下限和上限,依据式(3)计算各因素的零水平(Z0j)和变化区间(Δj),并对各因素按式(4)进行线性变换,最终得到各因素水平的编码表,如表1和表2所示。

表2 迎风/背风半路堑五个影响因素的水平取值Table 2 The horizontal value of the five influencing factors of the windward/leeward half cutting
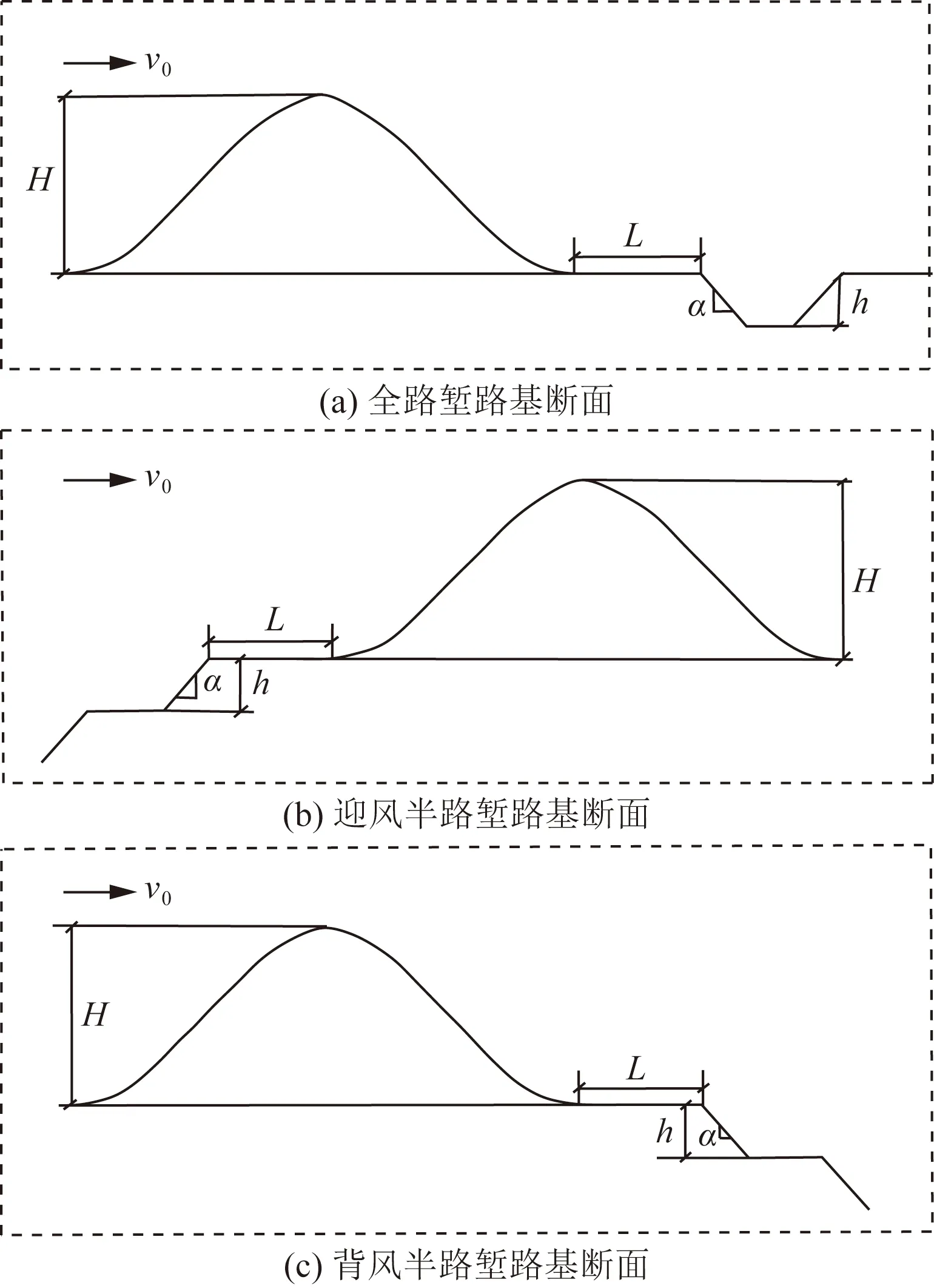
图1 风雪流主要影响因素示意图Fig.1 Schematic diagram of main influencing factors of snow drafting

(3)
式(3)中:γ为星号臂(值为1.547);Δj为偏离值。
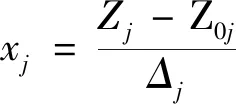
(4)
(3)正交试验。对3种路堑形式的路基断面按5因素3水平逐个进行二次正交试验设计,正交结构矩阵为包括各个独立变量xi、耦合项xixj及对平方项的中心化处理项x′i的27×21矩阵(表1),即每种路堑形式需进行27次试验,其中x′i是对平方项进行中心化处理后的结果,即

表1 全路堑影响因素水平表Table 1 The horizontal value of the influencing factors of the cutting
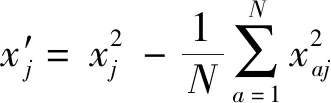
(5)
式(5)中:a为试验编号即正交表行号。
图2给出了3种情况下部分试验得到的风速场云图。
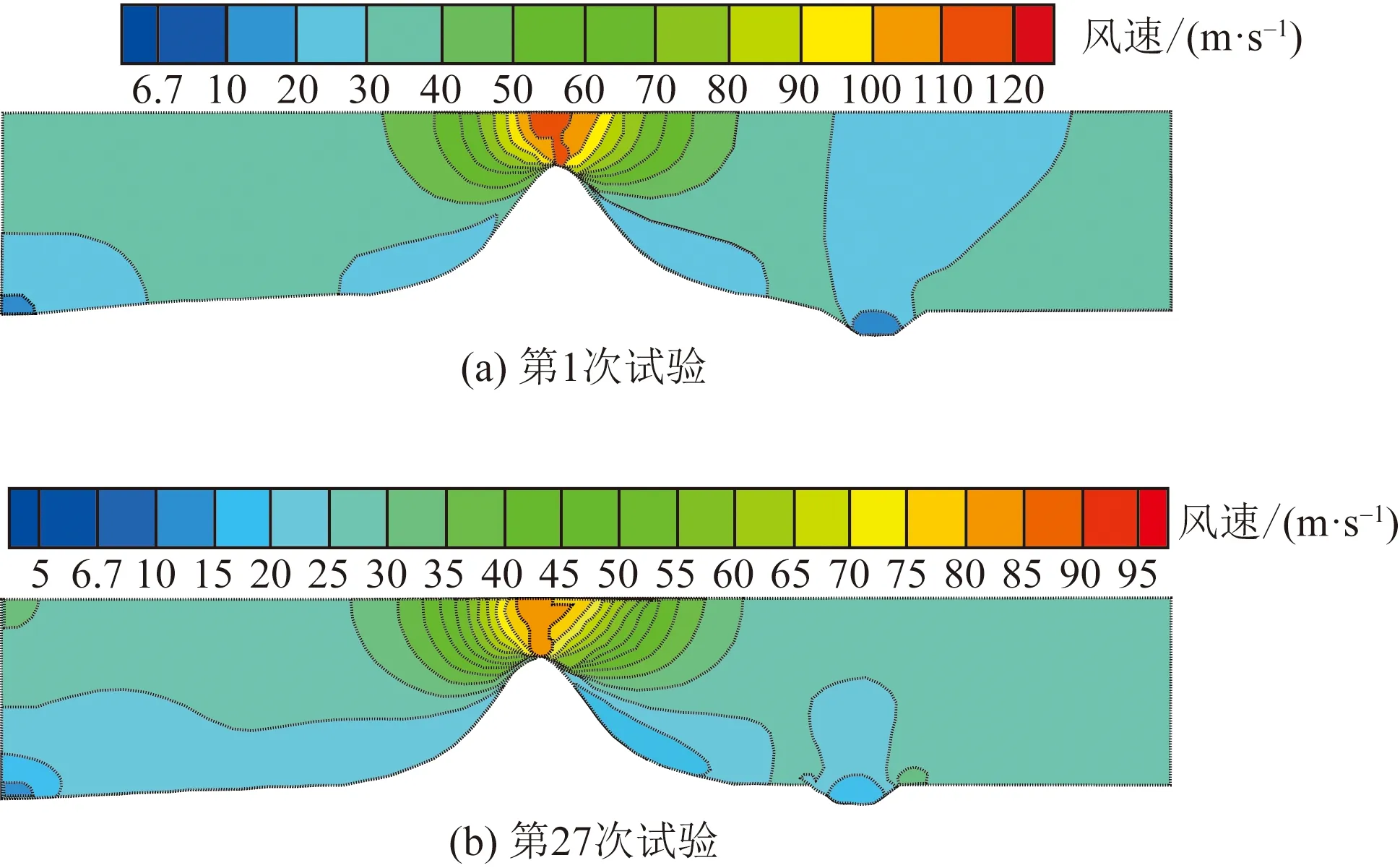
图2 全路堑风速场分布图Fig.2 Distribution of the wind velocity of the cutting
经过27次试验后,提取路堤表面风速小于雪颗粒启动风速的分布面积,得到试验目标函数的值,如图5所示。

图5 全路堑、迎风半路堑和背风半路堑27次试验目标函数值Fig.5 The objective function value of the cutting,windward half cutting and leeward half cutting experiment for 27 times
1.2 回归分析与预测模型
采用SPSS软件对3种路堑形式下得到的目标函数值并进行回归分析,建立回归方程。首先,建立考虑所有因素的饱和方程,即将所有xi、xixj和x′i均纳入回归方程建立的考虑范围,利用最小二乘法得到式(6)~式(8),分别对应全路堑、迎风半路堑和背风半路堑的路基断面形式。
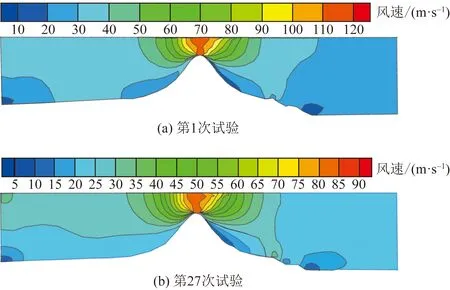
图4 背风半路堑风速场分布图Fig.4 Distribution of the wind velocity of the leeward half cutting
yc=3.016+0.374x1+0.366x2+0.976x3+
0.179x4-0.235x5+0.532x1x2+
0.233x1x3+0.166x1x4-0.183x1x5+
0.232x2x3+0.12x2x4-0.122x2x5-
0.243x3x4+0.162x3x5+0.002x4x5+
0.101x′1+0.108x′2+0.72x′3+
0.268x′4-0.174x′5
(6)
ywhc=10.045+0.035x1+0.037x2-0.617x3-
0.262x4-0.22x5-1.959x1x2+0.095x1x3+
1.958x1x4+1.897x1x5-0.059x2x3-
1.984x2x4-1.952x2x5+0.019x3x4+
0.072x3x5+1.901x4x5-7.645x′1-
7.646x′2-0.48x′3-0.21x′4-0.14x′5
(7)
ylhc=2.609+0.048x1+0.212x2+0.482x3+
0.018x4-0.305x5+0.036x1x2-0.126x1x3+
0.143x1x4+0.04x1x5+0.011x2x3+
0.24x2x4-0.071x2x5-0.283x3x4+
0.069x3x5-0.28x4x5-0.095x′1-
0.094x′2+0.065x′3+0.115x′4+0.034x′5
(8)
通过对上述饱和方程进行不敏感因素剔除和方差分析,得到更为简洁的回归方程[式(9)~式(11)]。
yc=3.016+0.374x1+0.366x2+0.976x3+

(9)
ywhc=223.757-1.959x1x2+1.958x1x4+
1.897x1x5-1.984x2x4+1.901x4x5-
7.645x′1-7.646x′2
(10)
ylhc=2.609+0.212x2+0.482x3-0.305x5-
0.126x1x3+0.143x1x4+0.24x2x4-
0.283x3x4-0.28x4x5
(11)
再将式(9)和式(10)中的平方项应用式(5)进行变换得到回归方程的另一种形式。
yc=2.461+0.374x1+0.366x2+0.976x3+

(12)
ywhc=235.162-1.959x1x2+1.958x1x4+
1.897x1x5-1.984x2x4-1.952x2x5+
(13)
最后,将式(4)代入式(11)、式(12)和式(13)中,最终得到三种路堑形式下路面积雪预测模型。
yc=15.045-0.077Z1-0.194Z2-1.077Z3+

(14)
ywhc=-178.949+6.97Z1+10.898Z2-
416.146Z4-10.919Z5-0.023ZzZ2+
3.04Z1Z4+0.047Z1Z5-6.089Z2Z4-
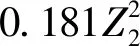
(15)
ylhc=-11.146-0.095Z1-0.399Z2+
1.2231Z3+16.392Z4+0.958Z5-
0.003Z1Z3+0.492Z1Z4+0.739Z2Z4-
1.451Z3Z4-1.805Z4Z5
(16)
由全路堑路面积雪预测公式[式(14)]得出:全路堑形式路基的风雪流灾害受山体相对高度、公路与山体横向距离及路堑深度这3种因素的影响,其影响程度排序为:路堑深度>公路与山体横向距离>山体相对高度。
由迎风半路堑路面积雪预测公式[式(15)]得出:迎风半路堑路基的风雪流灾害受山体相对高度、公路与山体横向距离、路堑坡度及10 m高处风速4种因素的影响,各因素影响程度排序为:路堑坡度>路堑坡度与10 m高处风速的耦合作用>10 m高处风速>公路与山体的横向距离>山体相对高度>公路与山体的横向距离与路堑坡度的耦合作用>山体相对高度与路堑坡度的耦合作用。
由背风半路堑路面积雪预测公式[式(16)]可知:背风半路堑路基风雪流灾害受山体相对高度、公路与山体横向距离、路堑深度、路堑坡度及10 m处风速五种因素的影响,各主要因素影响程度排序为:路堑坡度>路堑坡度与风速的耦合作用>路堑深度与路堑坡度耦合作用>路堑深度。
2 预测模型的应用与分析
以迎风半路堑预测模型为例,结合延崇高速公路对模型进行验证分析。图6为该高速公路主线上某段沿线地形图。将等高线进行立体还原得到了三维地形图,如图7所示。
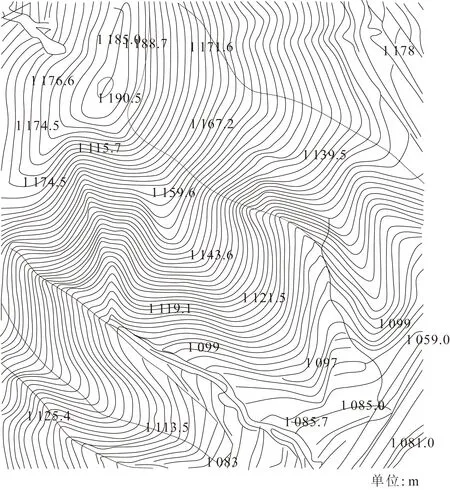
图6 延崇高速公路沿线某段地形等高线图(1∶1 000)Fig.6 Terrain contour map of a section along the Yanchong expressway(1∶1 000)
由图7中的3维立体地形图中截取一断面,如图8(a)所示。由地形信息可,公路路面高程为1 081.1 m,山体顶点高程为1 190.5 m,因此山体和公路的相对高程为109.4 m。另外,路基距离山脚的横向水平距离为17.49 m。根据延崇高速公路路基设计文件可知,路堑坡度为1∶1.5,路基宽度为26 m,路堑深度为10 m,据此可以建立数值几何模型,如图8(b)所示。这里初始风速取值与第2节相同。数值模拟结果如图9所示,图9(a)为计算域内的风速场整体分布云图。对应图8(b)中3号和4号子计算域内风速小于6.7 m/s的面积为3.43 m2,此时再将本工况下的风雪流影响因素,即山体相对高度、路基与山体横向距离、路堑深度、路堑坡度及10 m高度处风速带入预测模型式[式(15)],计算结果为3.58 m2,对比两者的结果可见直接应用回归方程计算结果与数值模拟结果相差不大,说明提出的预测模型具有一定的实用性。

图7 延崇高速公路沿线某段3维地形图Fig.7 A 3D topographic map of a section along the Yanchong expressway
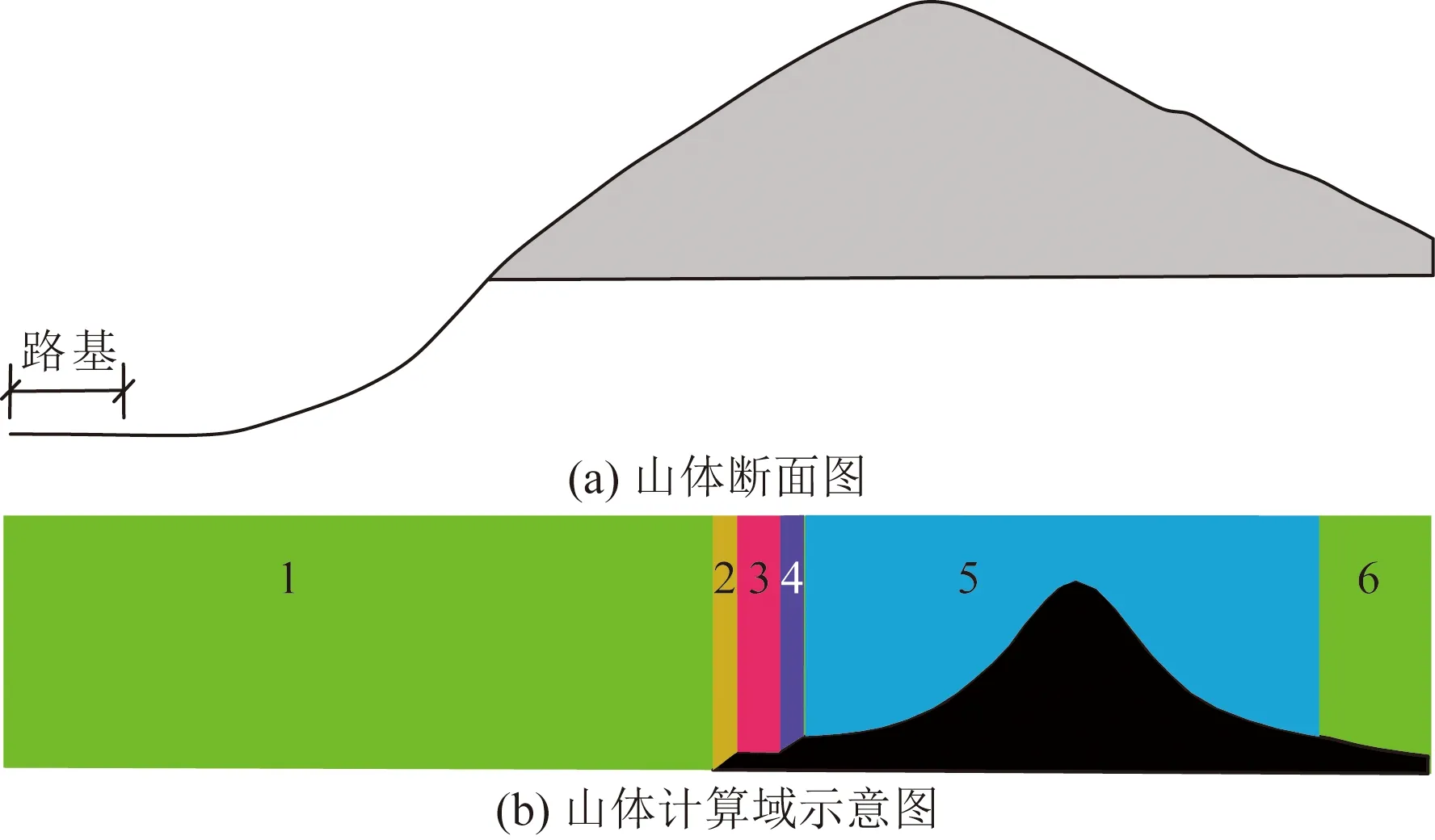
图8 典型迎风半路堑公路及其沿线山体的断面图和计算域示意图Fig.8 Section diagrams and computational domain diagrams of typical windward half-cutting highways and mountains along them
由图9(b)可以看出,风速减速区主要出现在公路表面及下风坡,由此可知,此区域容易出现积雪。假设该路段降中雪12 h,则积雪深度预测会有0.9~2.4 cm,若在降雪的同时伴随有风雪流发生,那么积雪厚度将会是无风雪流发生时积雪厚度的3~8倍,最大可达到19 cm,同时考虑到本例中半路堑的边坡坡角大于45°,则边坡几乎无储雪能力,因此,将会有大量积雪直接对基于路面,使得雪害程度进一步增大,非常不利于公路的安全有效运营。

图9 典型迎风半路堑路基断面风速分布图Fig.9 Distribution of the wind velocity of the windward half cutting
3 结 论
针对山区高速公路路堑风雪流灾害进行研究,对全路堑、迎风半路堑和背风半路堑3种路基形式下的风雪流流场进行数值模拟。主要结论如下。
(1)以路表风速小于雪颗粒启动风速的区域面积作为评价路面积雪的目标函数,以山体相对高度、路基与山体横向距离、路堑深度、路堑坡度及10 m高度处风速为主要影响因素,通过对3种路基形式进行正交试验,发现在路堑坡脚最易形成积雪,全路堑形式受路堑深度影响最大,迎风和背风半路堑形式则受路堑坡度及风速影响最大。
(2)经回归分析建立了风雪流灾害预测模型,并以迎风半路堑形式为例,对预测模型进行了应用分析,结果显示该模型预测结果与数值模拟结果误差不超过5%。研究对揭示风雪流致灾机理及其灾害预测奠定了基础。

