动力传动轴-机匣系统耦合振动特性
龙 伦,李 坚,赵勇铭,王 迪
(中国航发湖南动力机械研究所结构强度研究部,株洲 412002)
动力传动轴是直升机传动系统的重要动力传输部件之一[1-3],其一端与发动机连接,另一端通过联轴器(如膜盘、膜片)与主减速器相连,从而实现将发动机功率和转速传输到主减速器,因此其振动特性好坏直接影响到整个传动系统工作的稳定性。以往对于动力传动轴振动特性的研究主要集中在单个传动轴临界转速计算分析[4-6]、轴系的扭转分析[7-9]以及轴系齿轮系统动力特性分析[10-11]等,在这些分析中一般根据工程经验认为支承机匣刚性很强,忽略了支承机匣的柔性,从而造成了一定的计算误差,并且这种误差随着因支承机匣重量减轻、刚度减弱导致的转静子耦合动力特性越明显而越大,这严重地制约了直升机传动系统的动力学设计。针对以上情况,中外研究人员开展了相关研究工作,Guo等[12]开展了考虑柔性箱体结构的单级定轴齿轮箱振动特性研究;郭天才等[13]在尾减减速器机匣改进设计时避开了传动轴的共振频率;漆文凯等[14]进行了基于转静子耦合的组合压气机振动特性研究;许华超等[15]分析比较了耦合和不耦合柔性机匣结构时主减速器的振动特性,但在直升机传动系统中开展传动轴-机匣的耦合振动特性研究还比较少,并欠缺开展针对性的研究试验。
现以某型传动系统中的动力传动轴-减速器机匣为研究对象,建立考虑传动轴-机匣结构耦合振动分析模型,结合转静子系统耦合振动机理对计算结果进行分析,并开展试验验证。
1 转静子系统耦合振动机理
对于转子系统而言,系统的动能为

(1)
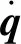
系统的应变能为
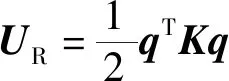
(2)
式(2)中:K为对称的刚度矩阵。
系统阻尼力的虚功为

(3)
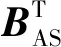
对于静子系统而言,系统的动能为

(4)
系统的应变能为
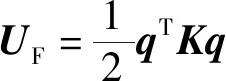
(5)
系统阻尼力的虚功为
δVF=-qTBδq
(6)
相互作用单元是指转子与静子之间的连接结构,如轴承等,其动力特性可以表示为

(7)
矩阵Kl和Bl可以分解成对称和反对称两部分,即

(8)
式(8)中:KS与定常弹性力有关,KAS与非定常弹性力有关,BS与陀螺力有关,BAS与结构阻尼力有关。
其虚功为
(9)
运用哈密尔顿原理,可得
(10)
式(10)中:δVe为激励力的虚功。
将式(1)~式(9)代入式(10)可得转静子系统的动力学方程为
(11)
当不考虑非线性连接力时,系统的齐次方程式可简化为

(11)
该方程的特征解和特征向量对应系统的固有频率和振型。从上述方程中可以看出,当相互作用单元对系统阻尼矩阵、刚度矩阵影响较大时,会出现不同于单独转子或静子系统的特征值和特征向量,即出现转静子系统耦合振动。
2 动力传动轴-机匣系统有限元建模
2.1 结构简介
某型传动系统如图1所示,系统通过动力传动轴转子组件实现减速传动,将发动机的输入转速及功率传递给主减主组件。动力传动轴转子组件分别安装在减速器机匣的左、右两侧,设计的输入转速为20 900 r/min,最大输入功率2 000 kW。
动力传动轴转子组件主要包括动力传动轴、输出锥齿轮、输入齿轮轴、膜片联轴器等零部件。其中输出锥齿轮通过前端的无内圈带安装边圆柱滚棒轴承(1#支承)及后端双排滚子轴承(2#支承)安装在减速器机匣的轴承座上,输入齿轮轴通过接触球轴承(3#支承、4#支承)支撑在试验器车台刚性机匣上,动力传动轴转子组件结构及安装示意图如图2所示。

图2 动力传动轴转子组件结构及安装示意图Fig.2 Schematic diagram of structure and installation of power transmission shaft rotor assembly
2.2 系统耦合振动分析模型
采用三维实体单元对动力传动轴-机匣系统进行网格划分,系统有限元模型如图3所示。模型中螺栓结构按等效质量和等效转动惯量以集中质量的方式施加;膜片联轴器结构采用弹簧单元模拟,弹簧单元刚度值通过实测膜片联轴器刚度获得,本系统中膜片联轴器的实测轴向、扭转、弯曲刚度分别为2.7×103、2.1×105和1.2×104N ·m/rad;根据系统所使用轴承滚珠数目、直径、接触角等参数,参照文献[16]中的轴承刚度近似公式求得4个轴承的刚度量级在108N/m,故模型中轴承刚度取1×108N/m。为了保证系统模型中转子部件与静子部件在连接处(轴承位置)的位移协调,模拟轴承的弹簧单元节点分别通过模型预测控制(model predictive control,MPC)的形式与转子部件、静子部件相关联。

图3 动力传动轴-机匣系统有限元模型Fig.3 Finite element model of the power driving shaft-casing system
考虑到系统中转子部件均采用不锈钢材料,材料阻尼较低,故仿真分析时只考虑系统的结构阻尼。根据工程经验,模型中系统结构阻尼比取0.02。
3 动力传动轴-机匣系统耦合振动分析
为了掌握动力传动轴-机匣系统在设计转速范围下的振动特性,对系统进行不平衡响应计算分析。分析中,在动力传动轴转子组件上施加转速、不平衡等载荷,不平衡量大小为20 g·mm,施加于右侧动力传动轴转子组件的输出锥齿轮的齿轮面上。提取与试验测试中振动加速度传感器布置位置(图3)相同处的节点振动响应,其中轴向、垂直、水平方向的振动速度响应-转速结果如图4所示,对应峰值转速下系统共振振型如图5所示。测点在25 000 r/min转速范围内存在4个峰值转速分别为13 200、15 000、16 800和21 600 r/min。
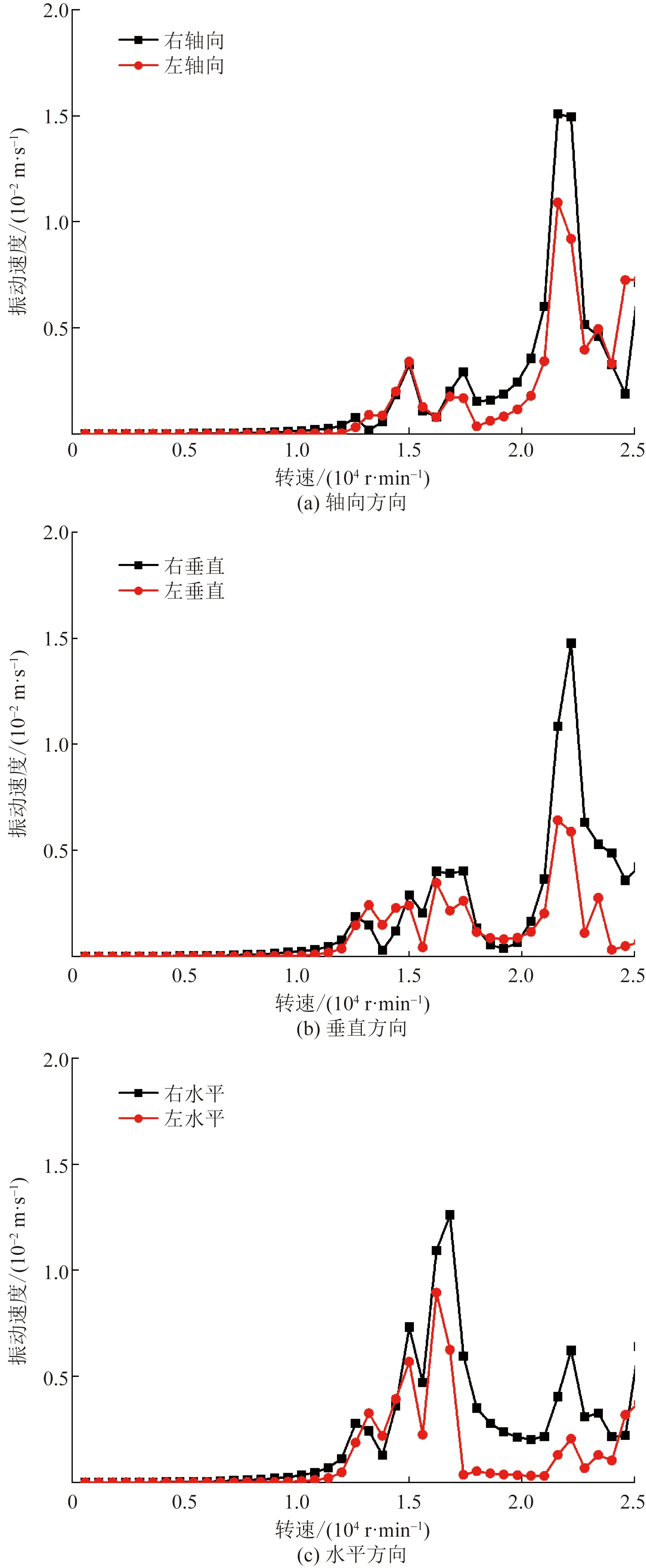
图4 不同方向振动速度响应-转速曲线Fig.4 Velocity response speed curves at different vibrations
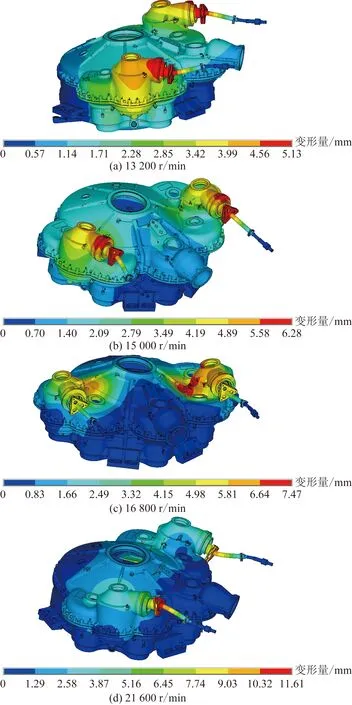
图5 不同峰值转速对应系统振型Fig.5 Different peak speed corresponding to system mode shape
系统在13 200 r/min峰值转速时,垂直、水平方向上的振动响应较大;在15 000 r/min和16 800 r/min峰值转速时,水平方向上的振动响应较大;在21 600 r/min峰值转速时,轴向、垂直方向上的振动响应较大。
系统13 200 r/min和15 000 r/min峰值转速对应的系统振型在连接处存在较大振动位移,结合本文第1节所述的系统耦合振动机理可知,该2阶振动为系统的耦合振动。其中13 200 r/min峰值转速对应振型主要表现为动力传动轴-机匣系统耦合的上下摆动,左、右振动测点位置垂直方向上的相位相差在180°左右;15 000 r/min峰值转速对应振型主要表现为动力传动轴-机匣系统耦合的左右摆动,左、右振动测点位置水平方向上的相位相差在180°左右。
系统16 800 r/min和21 600 r/min峰值转速对应振型分别为单独转子或静子系统的振动。其中16 800 r/min峰值转速对应振型主要表现为机匣振动;21 600 r/min峰值转速对应振型主要表现为动力传动轴转子组件的弯曲振动。
4 试验验证
4.1 试验测试装置及方案
为了验证分析的准确性,开展了动力传动轴转子组件动力特性试验。试验采用电机加增速箱的形式驱动动力传动轴,动力传动轴通过螺栓、膜片联轴器与法兰盘连接,将增速箱输入的转速、功率传递给与法兰盘花键连接的输出锥齿轮。为了测试系统的振动情况,在减速器机匣的左、右输入级端盖上端分别安装三向振动传感器,用于测试输入端的轴向、垂直、水平方向振动,详细试验装置及测试方案如图6所示。
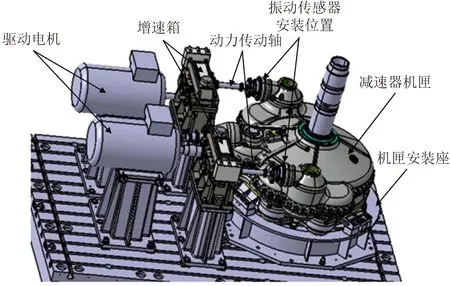
图6 试验装置及测试方案Fig.6 Test device and test scheme
4.2 试验结果分析
试验从0 r/min转速上推到了24 000 r/min,对右侧振动传感器采集的振动试验数据进行频谱分析,各方向上振动速度响应-频率曲线如图7所示,试验中出现的峰值转速与分析得到的峰值转速对比如表1所示。

表1 峰值转速对比Table 1 Comparison of peak speed

图7 不同方向振动速度响应-频率曲线Fig.7 Velocity response-frequency curve at different vibrations
试验过程中出现5个峰值转速,转速分别为8 500、12 600、15 600、18 600和22 800 r/min。
试验峰值转速与计算峰值转速结果的差异在10%以内。
系统在12 600 r/min和15 600 r/min转速(对应系统耦合振型)时的振动响应与22 800 r/min转速(对应单独转子振型)时的振动响应基本相当。
试验中出现了8 500 r/min峰值转速,其振动响应较小且主要表现为水平和垂直方向上的振动,推测该峰值转速对应的振型可能为动力传动轴转子组件的扭转振型,由于计算时约束了动力传动轴转子组件扭转方向的位移,造成该峰值转速在计算结果中未能出现。
为进一步验证分析中出现的耦合振型,绘制了左、右振动测点在试验峰值转速12 600 r/min和15 600 r/min处振动响应时域图,如图8所示。可以看出,12 600 r/min峰值转速下,左、右振动测点垂直方向振动响应相位相差180°;15 600 r/min峰值转速下,左、右振动测点水平方向振动响应相位相差180°,这与计算得到的耦合振型中左、右振动测点振动响应相位关系相一致,间接说明计算获得的这两阶耦合振型与试验中共振振型基本一致。

g为重力加速度图8 12 600 r/min和15 600 r/min峰值转速左、右振动测点水平方向时域图Fig.8 Time domain diagram of vertical direction of left and right vibration measuring points at 12 600 r/min and 15 600 r/min peak speed
5 结论
通过对某型动力传动轴-减速器机匣系统开展耦合振动分析和试验研究,获得主要结论如下。
(1)采用耦合振动分析得到的动力传动轴-机匣系统动力特性与试验情况吻合,计算精度在10%以内。
(2)转静子系统耦合振动与单独转子或静子系统振动具有同等的危害性,应尽量避免工作转速范围内的系统耦合振动。
(3)系统耦合振动分析除了可以获得单独组件系统振动特性以外,还可以得到系统的耦合振动特性,更全面地指导发动机传动系统的动力学设计。

