蒸发液滴内部Marangoni对流的分析与研究

胡晓玮，蒋鹤清,段淑娜，王晔春，赵 于，袁越锦*

(1.陕西科技大学 机电工程学院，陕西 西安 710021;2.西安交通大学 动力工程多相流国家重点实验室，陕西 西安 710049)

0 引言

液滴蒸发现象在自然界中普遍存在，已经受到广泛的关注与研究，如喷墨打印[1]、DNA芯片的制造[2]、固体表面上的颗粒沉积[3]、向内燃机中喷射燃油[4]、喷雾干燥技术[5]等.液滴蒸发过程包括液滴与外部环境的热量交换、动量交换及能量交换，以及液滴内部的流动与传热等，决定了相关工业工程及设备的效率，是实现强化传热传质过程的关键之一.

例如，燃油液滴的蒸发快慢及其与周围环境气体的混合程度直接决定了燃油火焰的燃烧效率、冷却塔水滴的蒸发则决定了冷却塔的换热效率、化工萃取过程中工质的蒸发决定了设备的传质效率等.影响液滴蒸发的因素主要有接触角、三相接触线、基板温度和液滴内部的微小流动等，随着研究的不断深入与累积，液滴内部的Marangoni流动在液滴蒸发过程中发挥的作用正被逐步揭示.

液滴在蒸发过程中，由于液滴弯曲的自由表面及不同的热通道长度，导致蒸发速率不均匀，温度分布不均匀，在自由表面形成温度梯度，从而引发表面张力梯度，形成Marangoni对流.Marangoni对流是一种与重力无关的、由表面引发的自然对流现象.Marangoni对流一般可由温度梯度和浓度梯度两种形式驱动，其中温度变化导致的Marangoni对流控制方式相对容易，可以较好地实现流动的调控.深入研究Marangoni对流在蒸发过程中的内在机理，有助于调控蒸发液滴的运动特性，进而改善工艺，增加产能，创大收益.

早在1986年，罗锐[6]研究了平板上蒸发液滴内部的微小流动对蒸发过程的影响；Hegseth等[7]通过实验研究展示了液滴内部的自然对流.随后，越来越多的学者致力于更为细致、微观的Marangoni对流研究.目前，Marangoni对流的研究方法主要有以下三种：实验观测法、理论分析法、数值模拟法.

在界面可见的尺度条件下，可通过添加示踪剂的方法来直接观测、研究Marangoni对流[8，9].例如，Schwabe[10]选择铝箔作为示踪剂，观察到微重力环境下加热的自由平液面上形成的Marangoni对流，研究发现Marangoni对流与马兰戈尼数Ma数密切相关.但由于添加了示踪流场的物质，会不同程度地影响流体界面的性质及相应的流场分布特性.

而光学测量法具有不受示踪剂影响、对流场介质无干扰的特点，因此被广泛应用于Marangoni对流的研究.于艺红等[11]通过激光纹影仪，直接在线监测界面的湍动对流结构，记录对流结构的变化过程，为以后的研究提供坚实的基础；沙勇等[12,13]利用竖直流动皂膜装置，使用纹影光学方法观察了由于丙酮从皂液中解吸，在微米级厚度皂膜上出现的滚筒状Marangoni对流结构.

然而，如何解释对流的微观不稳定性，以及宏观的流动演化过程，还需进一步借助理论及数值计算的分析.例如，Straub[14]研究了失重条件下，表面张力在两相流传热传质中的重要性，并理论分析了Marangoni效应对传热的影响；沙勇等[15]结合流体动力学条件，通过半经验模型及理论分析研究了Marangoni对流的传质机理，并得出传质舍伍德数Sh与马兰戈尼数Ma的关联；Hu等[16-18]采用润滑分析法对干燥液滴进行分析，并与流场的有限元算法相结合，得出表面活性剂能够抑制Marangoni对流的结论.大量的实验与分析结果不仅证明了Marangoni现象改善了传质过程，而且还可以将实际传递速度与理论估计结果进行比较，来量化临界Ma数和传递速率的关系.在数值分析方面，早在1991年，唐泽眉等[19]采用有限元数值模拟，考虑边界形状的影响，得出流场、温度场、表面压强的分布；刘春元[20]建立热毛细对流的数学模型并进行数值模拟，分别得到有无相变时的速度、温度分布；沙勇等[21]利用有机溶液能够使水的表面张力降低的特性，人工诱发Marangoni对流，进行数值模拟计算，研究了Marangoni对流对传质的影响；王贞涛等[22]建立了高温基板上的液滴蒸发与高温空气中的悬浮液滴蒸发模型，研究蒸发过程中液滴内部Marangoni对流非稳态流动模型；唐甜等[23]采用ALE方法建立固定接触角蒸发模型，数值模拟研究了蒸发数Ec、接触角θ对Marangoni对流的影响；Hu等[24]建立完善的蒸发模型，包括空气中的蒸发扩散，液体空气界面中的蒸发冷却，固体中的复合传热，浮力引起的对流和Marangoni对流，研究了加热和不加热基板上的蒸发特性.此外，还有很多学者对蒸发液滴的特性及诱导因素进行了大量的仿真模拟[25-28]，分别获得了在倾斜基板上、在油相中以及在激光照射下液滴内Marangoni对流的流动特性及其对传热传质过程的影响.

但是，目前的数值计算模型基板多为亲水性材料，液滴接触角在15 °～30 °之间，并没有对疏水性液滴内部的对流进行深入研究.本文以固定基板上蒸发液滴为研究对象，基于COMSOL Multiphysics创建流体计算模型，通过与Abdullah等[29]的实验结果进行对比验证分析，验证COMSOL Multiphysics数值模型的可靠性，并对接触角θ从100 °到120 °变化的蒸发液滴进行内部稳态流场特性分析，分析研究Marangoni对流的影响因素，为后续Marangoni对流的研究及优化提供相应的理论基础.

1 物理模型及网格划分

1.1 物理模型

利用COMSOL软件，建立的物理模型如图1所示，主要分为液相区域、气相区域两部分.液相区域为水滴，水滴半径R=0.7 mm，初始润湿半径为RC=0.6 mm，初始接触角θ=2.09 rad；基底长度为1.5RC，气相区域半径为25R.液滴静置于底层基板上，置于空气中.气、液两相工质分别为水、空气.采用二维轴对称模型，不考虑气相物质扩散.

图1 基底表面液滴蒸发示意图

1.2 网格独立性检验

蒸发液滴计算域网格的划分方法与模型的网格数量和网格质量有着直接的联系，而网格质量的好坏对数值仿真预测的结果具有一定的影响[30].因此，本文通过考察接触角θ=100 °，基板温度为300.15K，t=2 s时液滴内部最大流动速度，对计算模型进行网格无关性验证.t=2 s时液滴内部最大流动速度结果见表1所示.

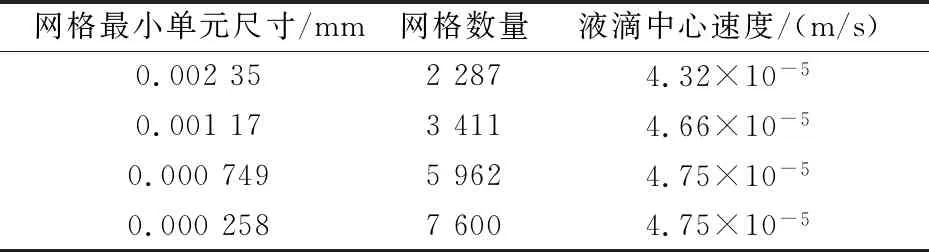
表1 网格无关性检验研究

从表1可以看出，当网格最小单元尺寸小于10-3mm时，对计算模型的结果影响较小，并且满足稳定性要求的步长.考虑计算时间和精度的影响，本文采取网格数量为5 962的网格.其中，网格划分时，为了使界面处具有较好的网格质量，主要对气液界面和液固界面进行网格加密处理.液滴内部的网格对结果的影响不大，相关网格加密示意图见图2所示.

因此，本研究中气液界面网格最小单元尺寸为0.000 217 mm，最大单元尺寸为0.041 1 mm，液固界面网格最小单元尺寸为0.000 749 mm，最大单元尺寸为0.026 2 mm，边界层层数3层，边界层拉伸因子1.2，所有域平均单元质量为0.903，网格数量约为5 962.

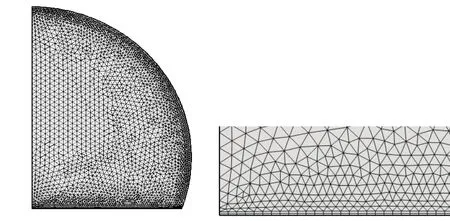
(a)网格划分示意图 (b)界面网格加密示意图 图2 网格划分及加密示意图

2 数学模型及边界条件

2.1 液滴内部流动及传热数学模型

本文选定COMSOL中层流流体流动、传热、Marangoni效应模型进行蒸发液滴仿真数值模拟计算.

液滴内部的流动及传热模型可以由以下方程组描述.

(1)连续方程

(1)

式(1)中：ρ为流体密度，kg/m3；V为流体的速度，m/s.

(2)动量方程(N-S方程)

(2)

式(2)中：P为流体微元体上的压力，Pa；μ为流体的动力粘度，Pa·s.

(3)能量方程

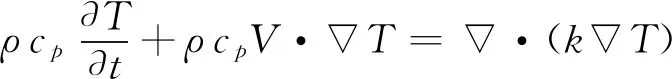
(3)

式(3)中：T为基板的温度，K；cp为流体的比热容，J/(kg·K)；k为流体的热导率，W/(m·K).

Marangoni效应在数值求解过程中是通过在N-S方程中添加额外的应力作用来考虑的，即由于在与表面相切的s方向上存在的表面张力梯度dσ/ds会对自由表面流动形成作用，因此就必然存在一个与s方向相反的剪切应力来保证表面的受力平衡.该剪切应力可能会改变边界条件，从而改变流动以及作用于液滴上的力.而产生该应力作用的表面张力梯度可由温度梯度、浓度梯度等诸多因素决定.研究人员发现，对于温度梯度产生的表面张力变化，在大部分温度范围内，表面张力随温度线性减小，直到临界点时减小为零.因此，对于任何给定的流体，对其热物理特性的dσ/dT进行控制总是确定的，并且接近常数[31].

空气中液滴表面的表面张力分布可以表示为：

(4)

假设热交换主要由热传导控制，则液滴表面无热量交换，那么利用拉普拉斯方程，可以得到：

(5)

式(4)、(5)中：R为液滴半径，m；σ为液滴的表面张力系数，N/m；θ为接触角，°；T为温度，K；x1是x方向上任意一点的位置.

为使问题简化，假设液滴是球形表面，法向方向上表面张力的差异非常小，法向的应力完全由表面张力决定.

根据这些假设，球形液滴的切应力边界条件就变为：

(6)

式(6)中：ρL为密度，kg/m3；vL为运动粘度，m2/s；u为速度，m/s.

那么根据方程得到作用于液滴上的力为：

(7)

除了法向阻力(第一项)外，在沿液滴表面张力减小的方向上还有一个Marangoni力2πR2(dσ/dx1)作用在液滴上.因此，表面张力随温度增加而降低.均匀温度梯度dT/dx1的存在就会使液滴在沿流体变热的方向上承受一个大小为2πR2(-dσ/dT)(dT/dx1)的附加力.

2.2 边界条件

(1)固液界面

固液两相接触界面采用无滑移边界条件，温度为常量.

V*=0

(8)

Θ=1

(9)

式(8)、(9)中：V*为壁面速度，Θ为热通量.

(2)自由表面

切向力的平衡以及垂直于表面方向上热通量的连续性，可用式(10)、(11)来表示：

(10)

(11)

式(10)、(11)中：Bi为毕渥数，Ma为马兰戈尼数，Pr为普朗特数.

依据上述建立的模型，对接触角为100 °、110 °、120 °，及基板温度为300.15 K、310.15 K、320.15 K时，蒸发液滴内部的Marangoni对流流场分布及基板温度对Marangoni效应的影响进行分析研究.

3 模拟结果及分析

3.1 模型验证

利用上述建立的模型，首先对Abdullah[29]等人的固着蒸发液滴的实验研究进行同条件下的数值模拟，验证模型正确性.图3为模拟得到的液滴内部各点速度大小与原文实验结果的对比.由图3可以看出，模型的计算结果与Abdullah[29]等的实验结果吻合较好，模型正确可靠.

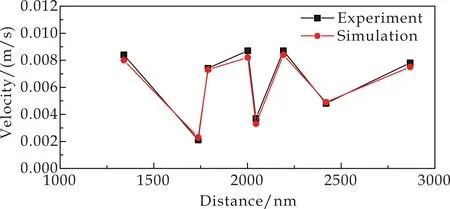
图3 液滴内部速度的模拟与实验结果对比验证

3.2 蒸发液滴内部Marangoni对流

3.2.1 Marangoni对流发展规律

初始状态下，基板与液滴之间存在温差，所以在基板和液滴之间会发生传热，在传热过程中产生温度梯度，从而驱动液滴界面的表面张力梯度，诱发Marangoni对流.图4～8分别为t=0.05 s、0.1 s、0.15 s、0.2 s、0.3 s时液滴内部的流场分布图(a)及温度分布图(b).

从瞬态速度图可以看出，初始阶段(t=0～0.05 s时)在液滴中下部出现小涡流，此时液滴边缘界面处速度最大，且随着时间变化界面速度不断增大，涡流不断变大.t=0～0.05 s内，速度最大为4×10-6m/s，在t=0.2 s时达到1.2×10-5m/s，说明对流产生的机理是由于表面张力梯度的存在，在表面诱发，传递到液滴内部.

从温度分布图可以看出，t=0.05 s时，热量从基板传递到液滴内部，三相界面处热量传递速率比液滴内部的传递速率大，这也是液滴中下部最先出现涡流的原因.t=0.2 s以后，液滴内部速度最大区域始终在液滴中心及界面处；速度及温度分布变化较小，说明t=0.2 s时内部流动达到稳态.

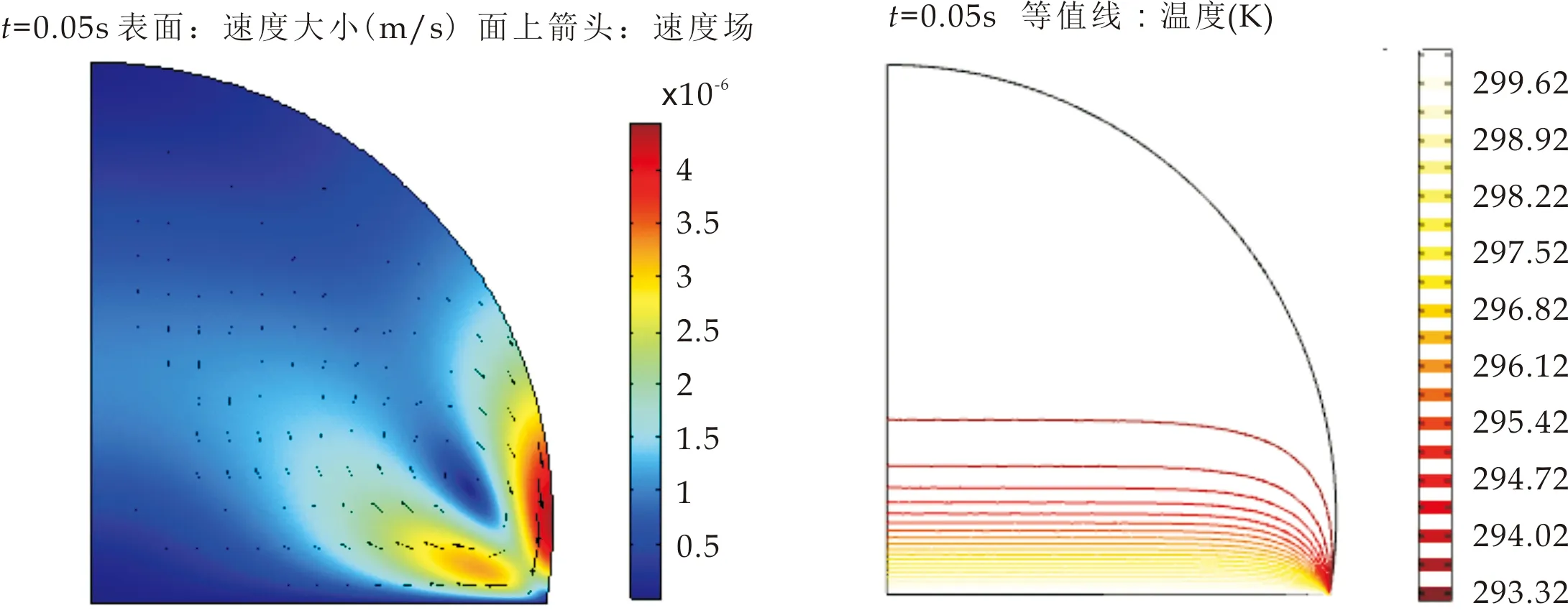
(a)速度矢量分布 (b)温度分布图4 t=0.05 s时液滴内部流场分布及温度分布

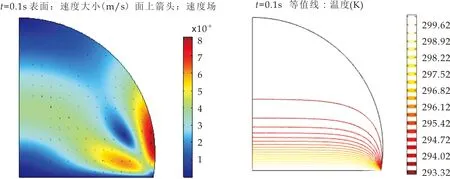
(a)速度矢量分布 (b)温度分布图5 t=0.1 s时液滴内部流场分布及温度分布

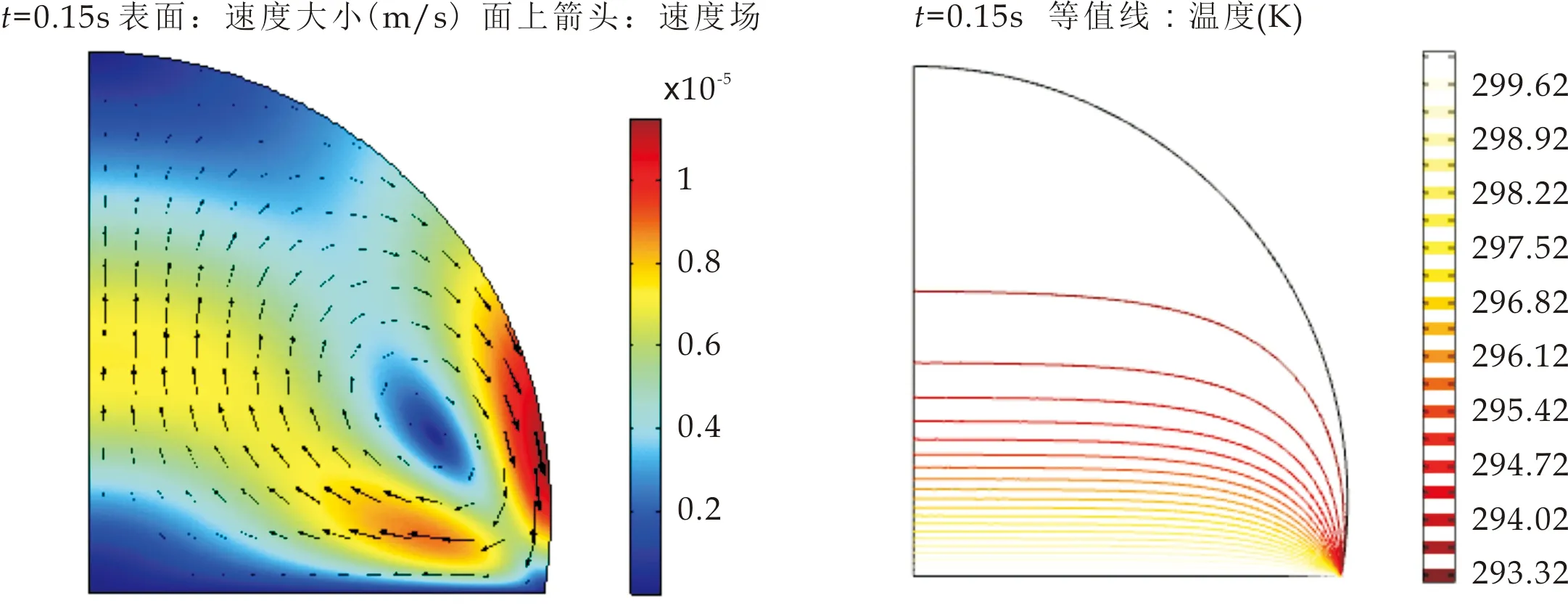
(a)速度矢量分布 (b)温度分布图6 t=0.15 s时液滴内部流场分布及温度分布

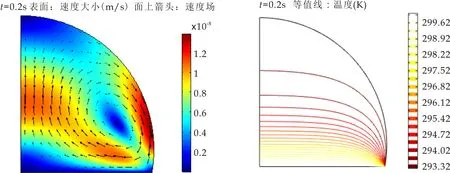
(a)速度矢量分布 (b)温度分布图7 t=0.2 s时液滴内部流场分布及温度分布

(a)速度矢量分布 (b)温度分布图8 t=0.3 s时液滴内部流场分布及温度分布

3.2.2 基板温度对Marangoni对流的影响

图9～11展示的是接触角θ1=100 °和基板温度分别为300.15 K、310.15 K、320.15 K时，液滴内部Marangoni对流达到稳态时的温度分布及速度分布.从图中可以看出，基板温度越高，导致基板和液滴之间温度梯度增大，所以对流速度越大，Marangoni效应越明显.在接触角相同的情况下，由于基板温度不同，液滴蒸发速度不同，基板温度从300.15 K至320.15 K变化，最大速度由4.77×10-5m/s变为2.06×10-4m/s.

由图可以很明显地看出，轴对称模型左侧部分速度较大，即液滴中心速度比边缘速度大，这是由于达到稳态后，热量向液滴中心传递速度比向液滴边缘传递速度快.而相对应的温度分布图中，随着基板温度增大，等温线趋势不变，但液滴内最大温度由299.63 K增至318.13 K，同水平线上液滴中心的温度高于界面的温度.

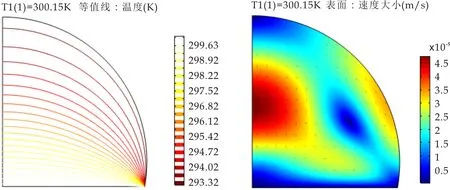
(a)温度分布 (b)速度矢量分布图9 T1=300.15 K时温度分布及速度矢量分布

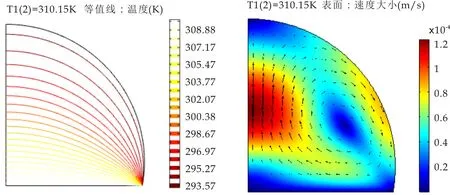
(a)温度分布 (b)速度矢量分布图10 T1=310.15 K时温度分布及速度矢量分布

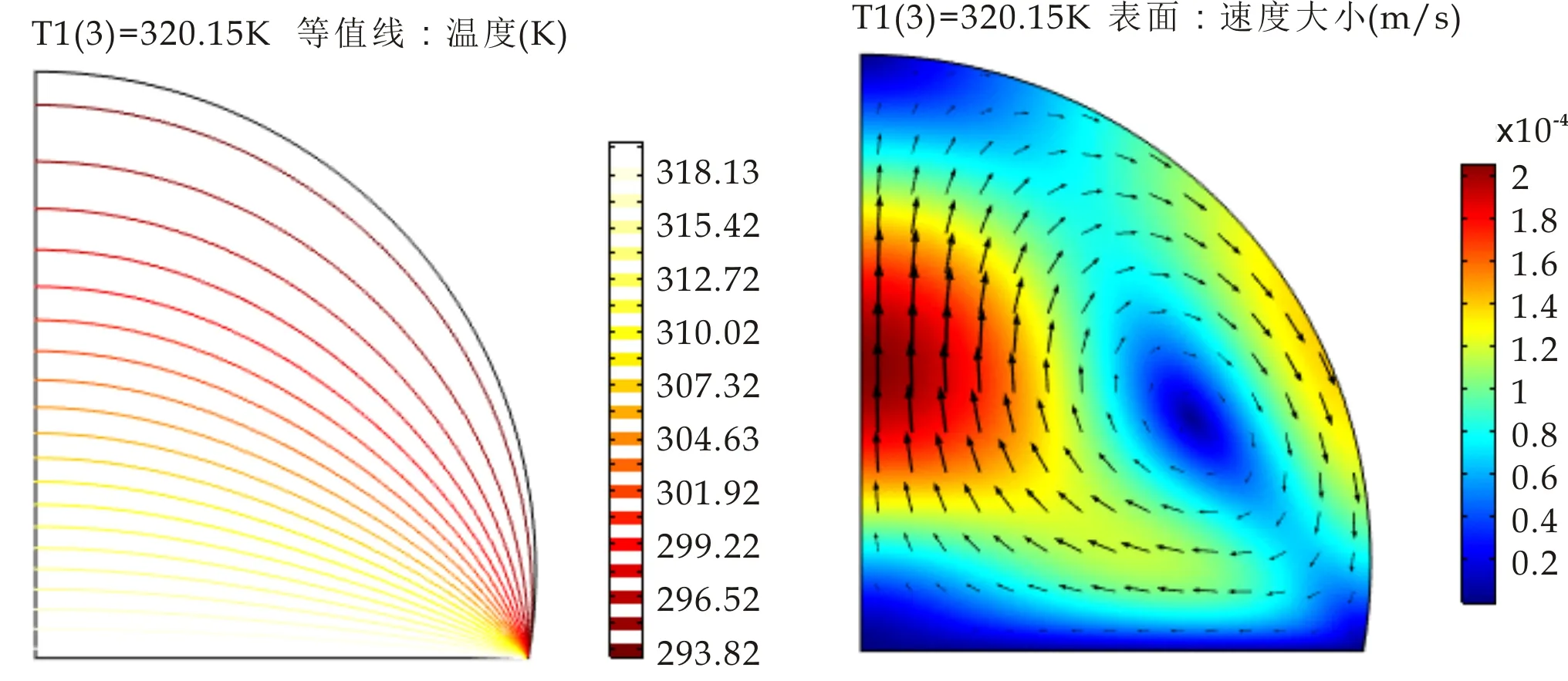
(a)温度分布 (b)速度矢量分布图11 T1=320.15 K时温度分布及速度矢量分布

3.2.3 接触角对Marangoni对流的影响

图12～14分别展示的是接触角为θ1=100 °、θ1=110 °、θ1=120 °和基板温度为300.15 K时，液滴达到稳态时的三维速度分布及速度矢量分布.从图12～14可以看出，随着接触角的增大，传热区域也随之增大，液滴内部流动速度相对增大，液滴内部最大速度由4.77×10-5m/s增加至7×10-5m/s，可以发现接触角对流动速度有增强作用.

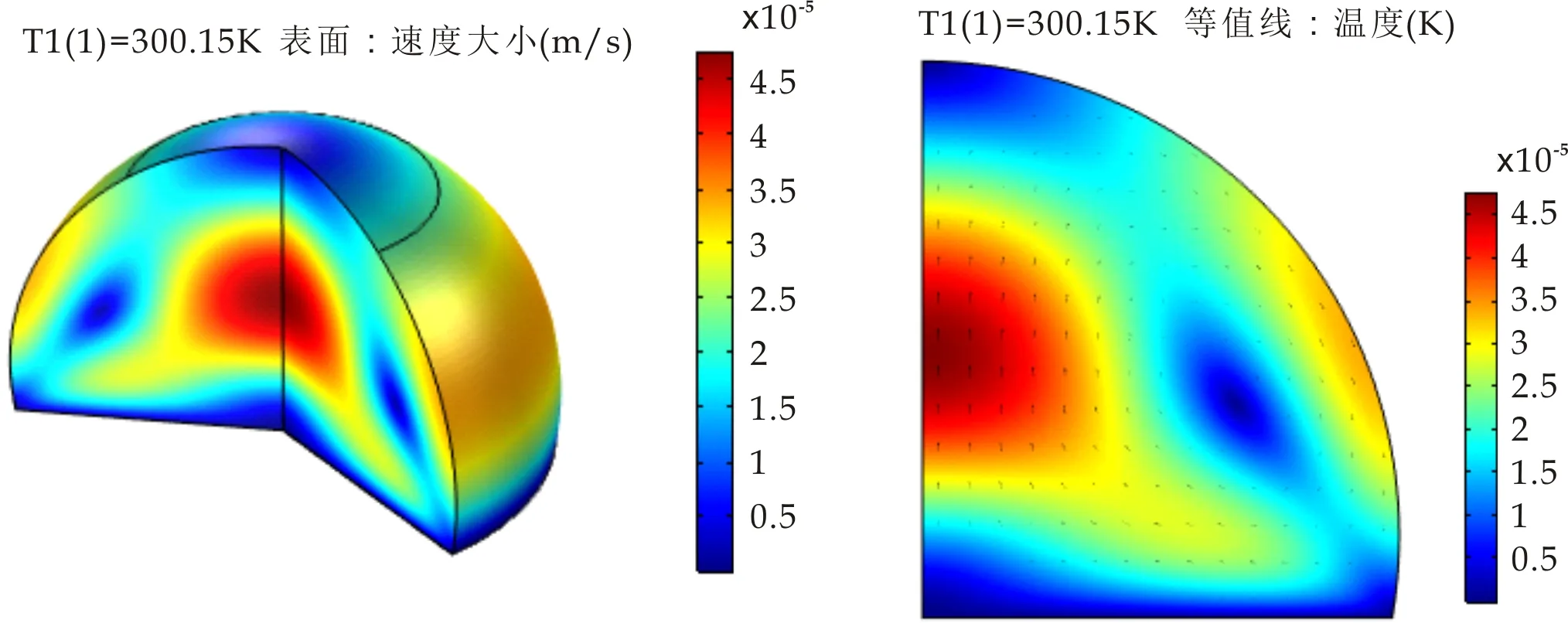
(a)三维速度分布 (b)速度矢量分布图12 θ1=100 °三维速度分布及速度矢量分布

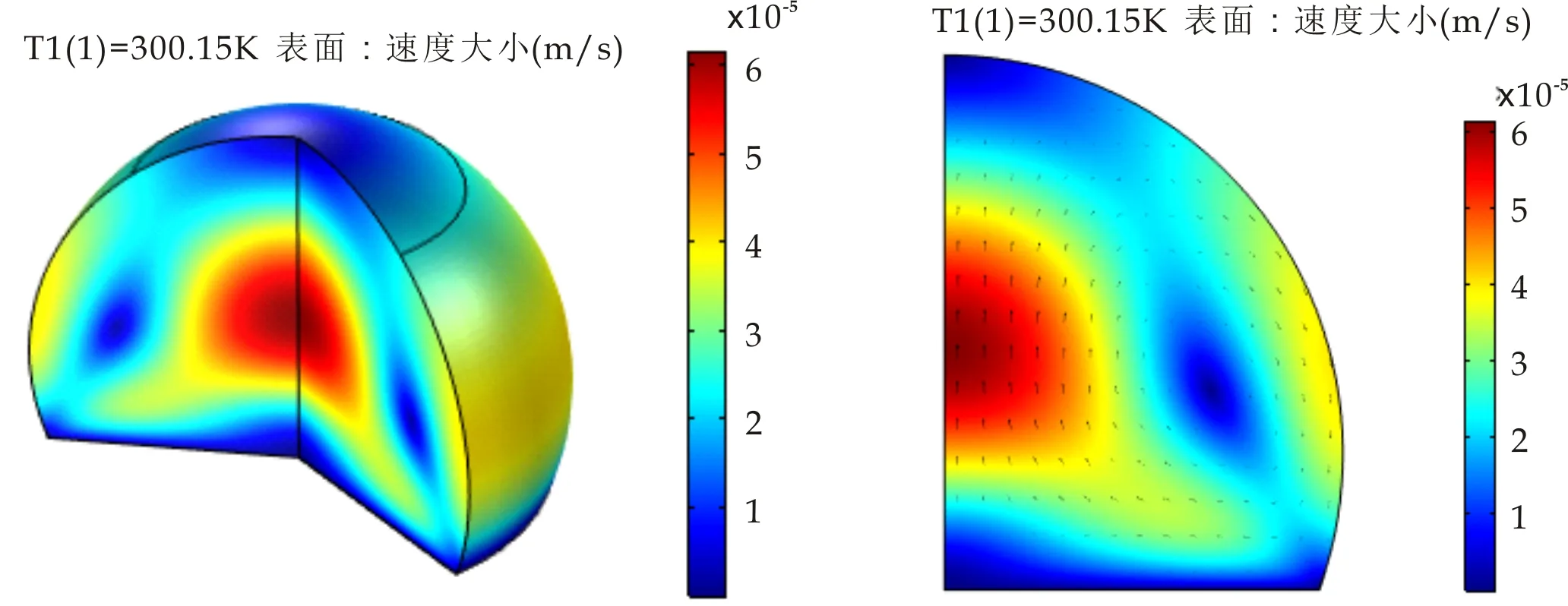
(a)三维速度分布 (b)速度矢量分布图13 θ1=110 °三维速度分布及速度矢量分布

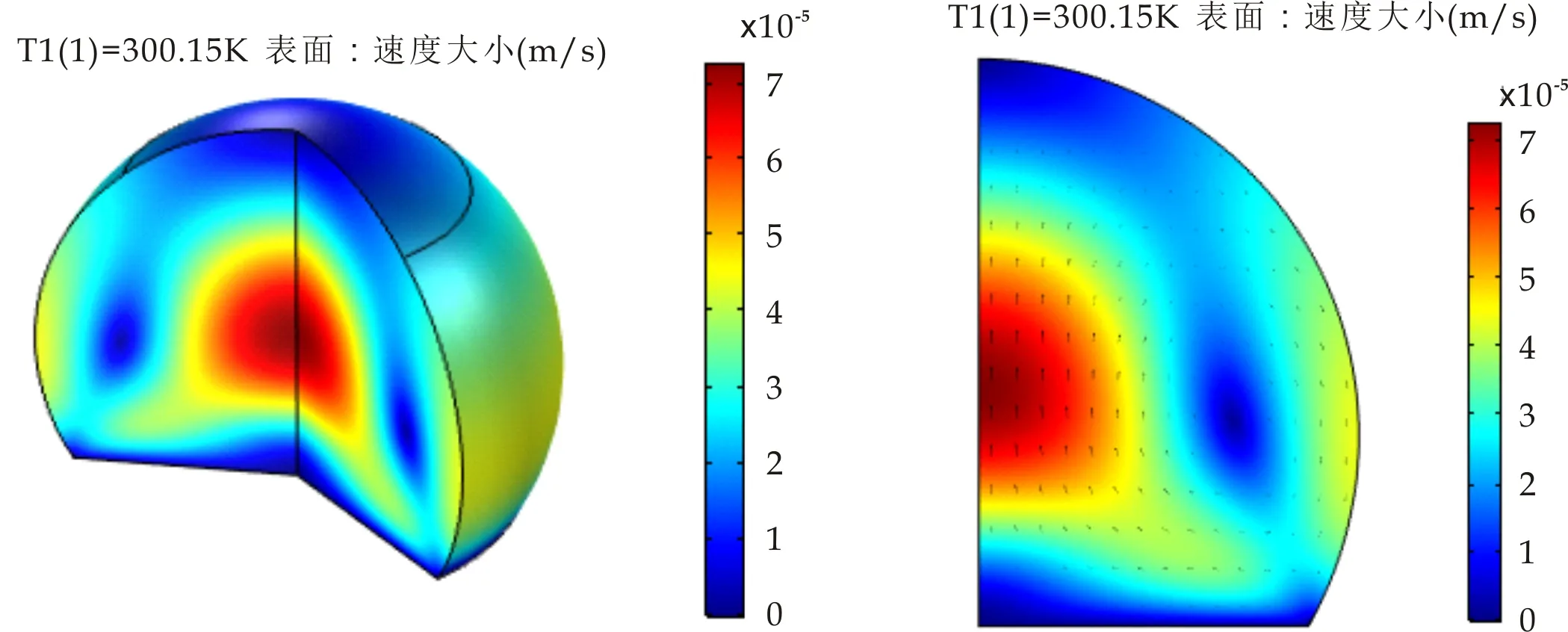
(a)三维速度分布 (b)速度矢量分布图14 θ1=120 °三维速度分布及速度矢量分布

3.3 最大对流速度

本文分别对接触角为100 °、110 °、120 °，基板温度为300.15 K、310.15 K、320.15 K时的液滴进行模拟，得出速度分布及温度分布.初始阶段液滴边缘界面处速度最大，随着时间变化，液滴达到稳态，液滴内部速度不断增大，最终液滴内部速度较大区域分布在液滴中心及界面处.

图15显示的是不同接触角及基板温度对液滴内最大速度的影响.液滴最大流动速度随基板温度的升高及接触角的增大而增大.接触角越大，流动速度随基板温度增加的越快，这是由于液滴内部与界面温差增大和接触角增大共同作用的结果.基板温度升高时，Marangoni对流强化作用越明显.

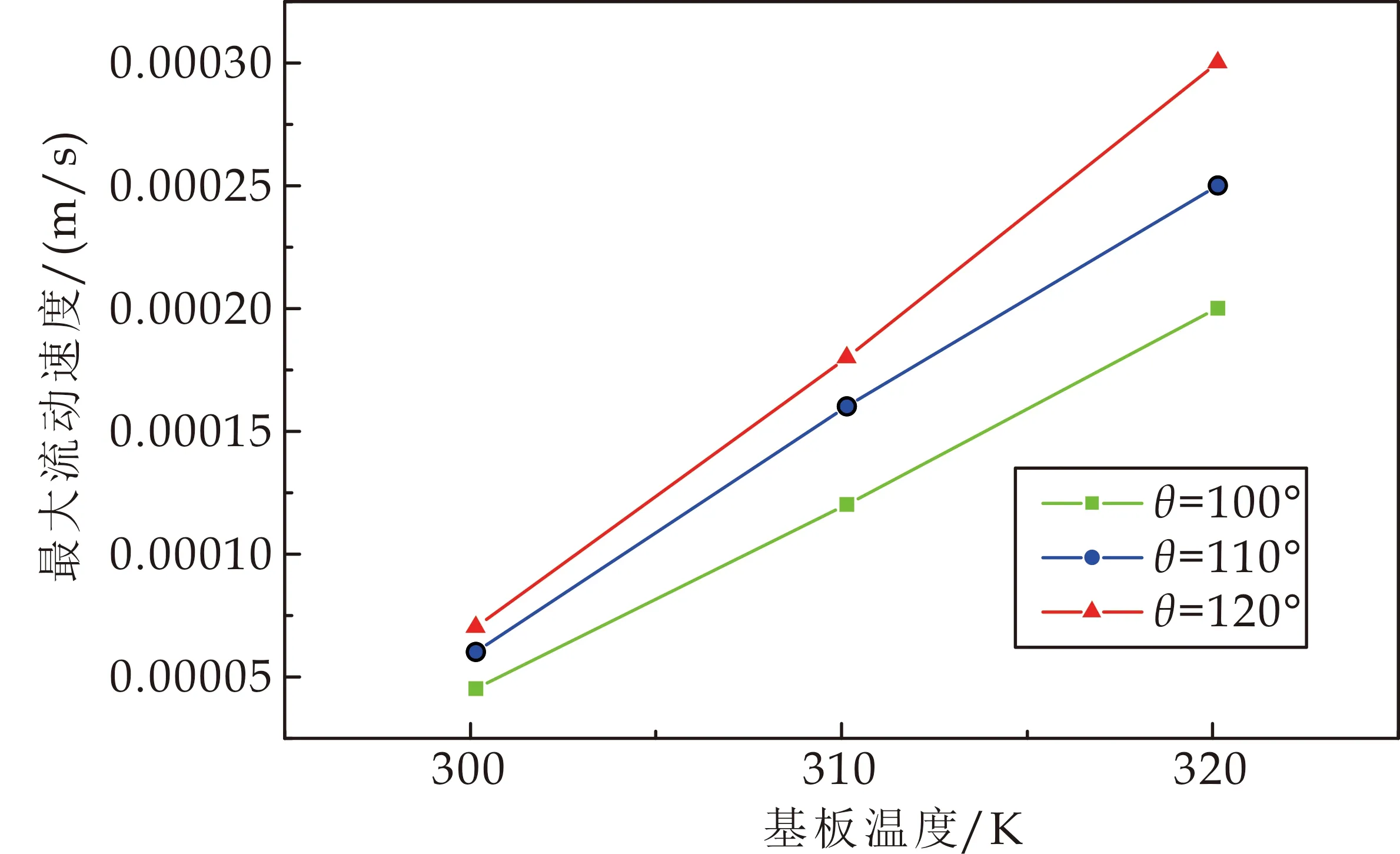
图15 液滴接触角与基板温度对最大对流速度的影响

4 结论

(1)作瞬态研究时，初始阶段液滴边缘速度最大，这是由于界面温度梯度引发的Marangoni对流在表面诱发，向内部传递，t=0.2 s后内部流动达到稳态，液滴中心速度逐渐增大，直至与界面速度相同.

(2)达到稳态后，基板温度固定不变时，接触角从100 °到120 °变化，液滴内部速度不断变大，这是由于接触角的增大使液相区域增大，传热区域增大，导致涡流变大，速度增强，说明在一定范围内接触角的增大可强化Marangoni对流.

(3)达到稳态后，接触角固定不变时，基板温度从300.15 K到320.15 K变化，与环境温度形成的温差变大，由温度梯度引起的Marangoni效应增强，液滴内部流动速度增大.基板温度越高，Marangoni效应形成的涡流结构就越明显，说明基板温度的提高有利于相际间的传热.