5维三次-五次散焦非线性薛定谔方程的数值模拟
丁 聪,丁根宏
(河海大学 理学院,江苏 南京 211100)
0 引言
本文主要研究5维三次-五次非线性薛定谔方程:
iut+Δu=|u|2u+ε|u|4u
(1)
其中u:R5×R→C,ε=1.非线性薛定谔方程是量子力学和非线性光学中的重要模型,主要用于模拟波色-爱因斯坦凝聚和电磁波在非线性介质中的传播.方程(1)有两个重要的守恒量.
质量为:
(2)
能量为:
(3)
过去三十年中,人们从理论和数值上对非线性薛定谔方程的解做了大量的研究工作.其中理论上,主要研究工作围绕非线性薛定谔方程的长时间行为,其中包括J.Bourgain[1],J.Colliander[2],C.E.Kenig 和 F.Merle[3,4]等.另一方面,在非线性薛定谔方程的数值模拟上,很多专家做了重要的研究工作,例如Q S Chang等[5]对于三种非线性薛定谔方程模型,给出了八种差分格式并比较了它们的优缺点,T R Taha等[6]采用有限差分法和有限傅里叶变化法近似非线性薛定谔方程,比较了各种方法的优缺点,为后续研究非线性薛定谔方程解的行为提供了参考.继差分法后,有限元法和谱方法也相继被用于薛定谔方程解的行为分析中[7,8],但这些方法无法运用于高维非径向方程解的行为分析中.近年来,采用深度学习的方法求解偏微分方程的解,尤其对于高维偏微分方程求解的应用引起广泛关注[9].
本文主要采用有限差分等数值方法研究5维三次-五次非线性薛定谔方程(1)在径向情形下解的Sobolev范数H2的有界性.此方程是2维三次-五次非线性薛定谔方程在高维的非聚焦形式,参看Cheng X[10]关于2维情形的重要研究工作.对于有界临界范数假设,在3维三次散焦非线性薛定谔方程情形下,解的Sobolev范数H1/2有界性已有严谨的理论证明[7],但对于5维三次-五次散焦非线性薛定谔方程情形下解的Sobolev范数H2有界性假设的理论证明还未解决.
本文借鉴文献[11],尝试采用数值的方法研究其解的行为.通过对几个重要的初始函数:高斯型函数、环型函数、振荡高斯型函数进行数值实验,运用有限差分方法,参考文献[12],观察方程解的‖Δu‖L2和‖Δu‖L14范数值,结合数值模拟的结果,根据逼近原理,得到解的H2范数随着时间的推移而增加,但是在一定时间后解的H2范数值趋于稳定,这个值高于t=0时解的H2范数值.
1 数值方法
1.1 时间离散
本文研究方程(1)的径向对称形式:
(4)
此情况下H2受控制于‖Δu‖L2.本文取r∈(0,Rmax),边界条件是:
ur|r=0=0,u(r=Rmax)=0
(5)
空间离散形式,其中h=Rmax/J:
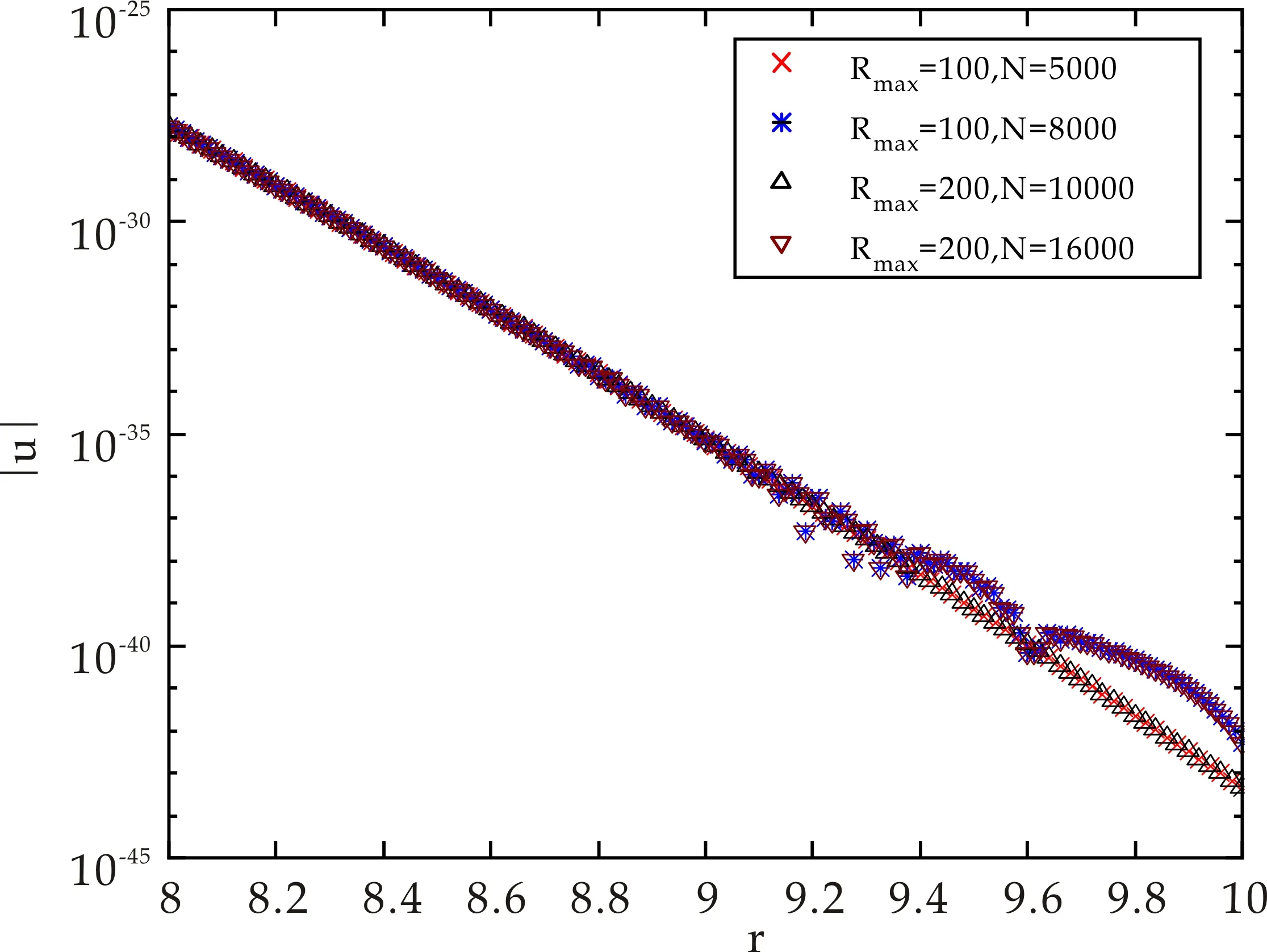
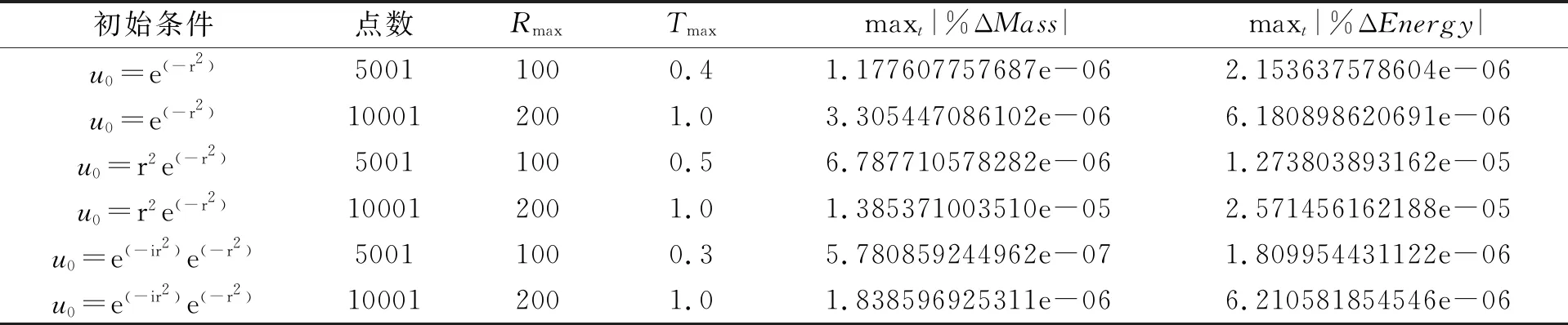
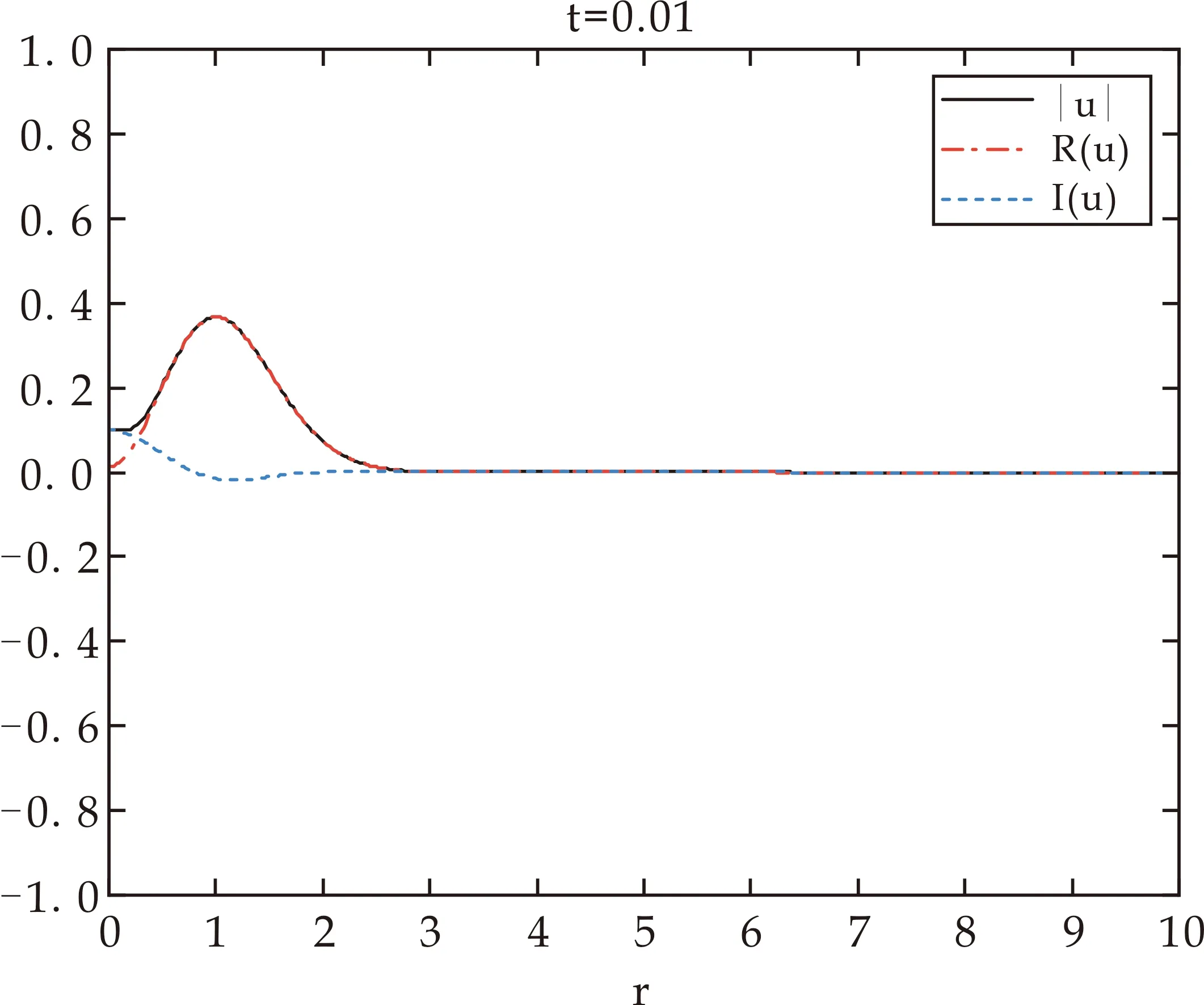
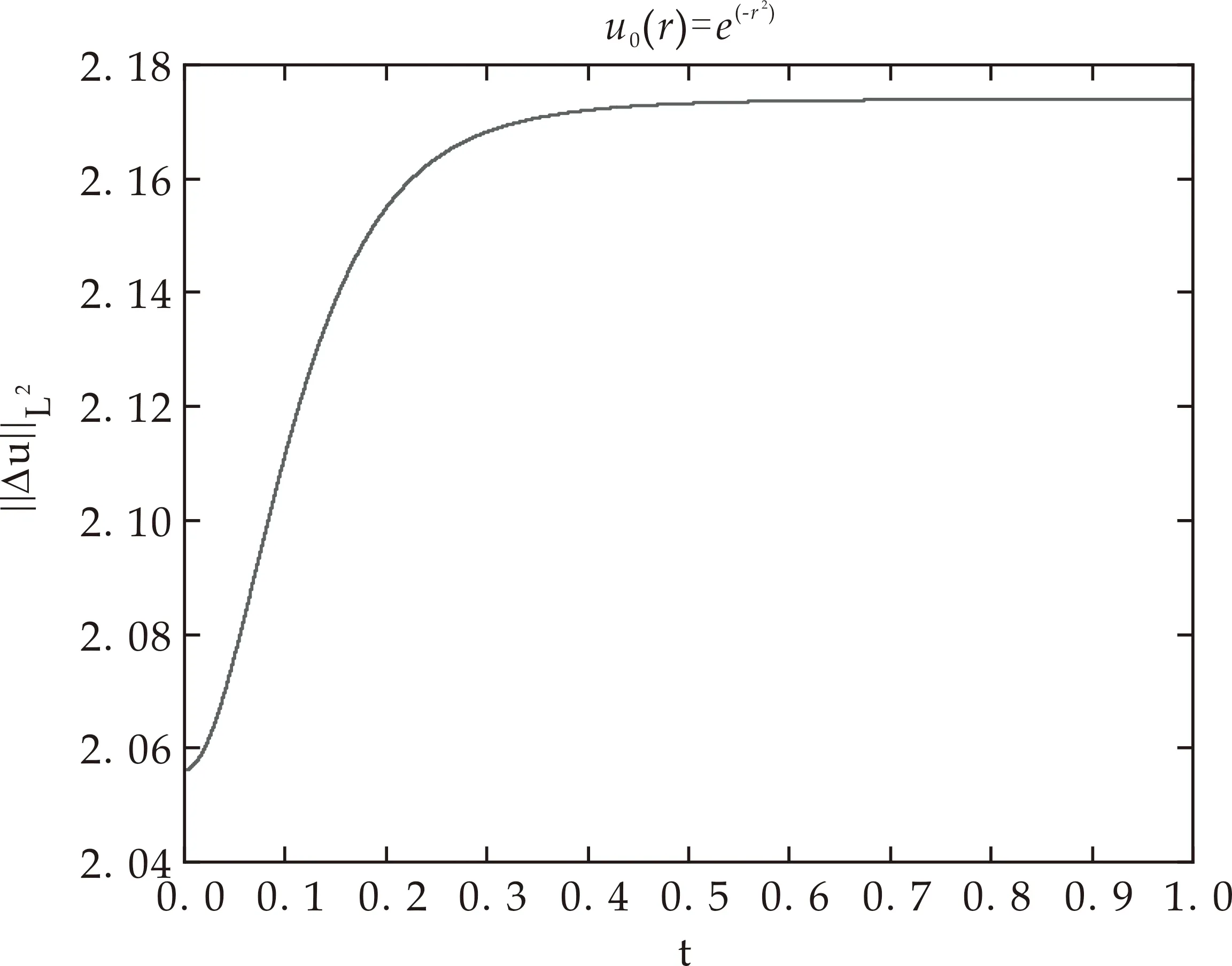
0=r0<… (6) 时间离散形式,其中τ=T/N: 0=t0<… (7) 对于式(4)本文采用如下的差分形式: (8) 其中: 离散边界条件: u-1=u1,u-2=u2 uJ+1=0,uJ+2=0 对于两个守恒量,其离散形式如下: 质量 (9) 能量 (10) 在L2空间内,定义内积: 其离散形式如下: 定理1设方程(4)、(5)有解u(r,t),且解v(r,t)∈C5×C1,则差分格式(8)的解收敛到方程(4)、(5)的解,且收敛阶数为O(τ+h3). (11) (12) 两边取模开方,又由v(r,t)∈C5×C1,结合柯西不等式得: ‖en+1‖2-‖en‖2≤Cτ‖Ern‖2+ Cτ(‖en+1‖2+‖en‖2) 整理得: (1-Cτ)(‖en+1‖2-‖en‖2)≤Cτ‖Ern‖2+2Cτ‖en‖2 若τ取的足够小,使得Cτ≪1,则有1-Cτ>0,在对于式(15)两边关于n在1到N-1上求和得: (1-Cτ)‖eN‖2≤(1-Cτ)‖e0‖2+ 结合离散Gronwall不等式,对上式处理可得: ‖en‖2≤CO(τ+h3) 证毕. 在无量纲情形下,本文通过计算模拟定初始条件下,对于不同空间离散的情形,定时刻|u|的尾部情况和在定初始条件下两个守恒量的相对误差以达到数值验证本文采用的差分格式的稳定性的目的.图1显示:在固定时间分辨率下,对于初始值u0=r2e(-r2),|u|的尾部情形,观察到在不同空间离散情况下,尾部图像点集重合度较高,但在区间[9.2,10]上有所分歧.经过观察发现当Rmax=200,N=16 000和Rmax=100,N=8 000时,尾部值曲线形态相对较差.另两种空间离散情况,尾部曲线形态光滑,效果较好. 图1 对于u0=e(-r2)在t=0.01时,|u|的尾部变化 再来验证守恒量数值的稳定性,表1显示了在三种固定初始条件,不同的时空分辨率两个守恒量的相对误差.发现守恒量误差处于E-05~E-07量级之间,鉴于本文模拟对象的数值量级在E+00~E+02量级之间,且只是验证其有界性并无太高精度要求,故算法满足本文计算需求.上述两种方法数值验证了本文采用的差分格式的稳定性.比较不同时空分辨率下的数值结果,决定下文数值模拟统一在Rmax=200,N=10 000情况下进行.至此本文分别使用理论分析和数值实验验证了本文采用的差分格式的收敛性和稳定性. 表1 在不同模拟下的守恒量的相对误差 本文考虑以下几类初始条件: 高斯型函数: u0(r)=Ae(-r2) 环型函数: u0=Ae(-α·i·r2)e(-r2) 震荡高斯型函数: u0=Ar2*e(-r2) 本文主要目的是采用数值的方法验证解的Sobolev范数H2的有界性,则A值无需过大,取A=1,α=1. 观察图像是否变得渐近.当模拟运行足够长的时间,对于临界范数H2,由于数值上更便于观察‖Δu‖L2,且: ‖u‖H2≤C‖Δu‖L2 ‖Δu‖L2控制H2,若‖Δu‖L2有界就保证H2范数的有界性,于是观察‖Δu‖L2的数值情况.实验模拟‖Δu‖L2,如果其有界,根据文献[13,14]中的基础假设,若标度不变,范数在时间上是全局有界. 本文共模拟了三种初始条件.其中,图2(a)、(b)、(c)展示了高斯型初始条件u0(r)=e(-r2)随着时间t的数值演变过程,|u|是单调递减的,并随着时间震荡.图2(d)、(e)、(f)展示了震荡高斯型初始条件u0(r)=e(-ir2)e(-r2)演变过程,形态同高斯型相似,震荡并最终衰减. (a)u0(r)=e(-r2)在t=0.01时 图3(a)、(b)、(c)展示了环形初始条件u0(r)=r2e(-r2),最初|u|聚焦于原点,但快速松弛,然后同高斯型初始条件相似,开始震荡衰减.对于三类初始条件,解都保持光滑,并且在振幅上单调衰减.图3(d)、(e)、(f)在三类初始状态中,‖u‖L6值最终衰减到0,表明势能衰减到0,能量集中于动能,符合预期. (a)u0(r)=r2e(-r2)在t=0.01时 进一步定量评估散射,在图4(a)、(b)、(c)中,展示了‖Δu‖L2的变化,其值迅速饱和,且饱和值大于初始值,则受其控制的H2范数有界.环型和震荡高斯型初始值不同于高斯型的单调增,它们在大趋势上都是先减小后增大走势同他们的‖u‖L6值走势相反. 在图4(d)、(e)、(f)中绘制了一段时间下L14范数图像,其在一定时间内量级变化不大,然后快速渐近,根据Strichartz估计,则H2范数有界且快速渐近.通过以上模拟,得出H2范数值在一段时间内有界,且H2范数值随着时间推移快速增加到一个略大于t=0时的值后保持不变. (a)u0(r)=e(-r2)时‖Δu‖L2在时间上的变化 本文首次采用数值的方法证明三次-五次非线性薛定谔方程解的H2范数有界性.通过构造收敛的差分格式,借用Matlab进行数值计算,模拟5维三次-五次非线性薛定谔方程解的‖Δu‖L2范数变化和‖u‖L14范数的渐进性,逼近解的H2范数.从数值结果来看,各项模拟达到预期,数值上验证了解的H2范数的有界性假设.接下来的工作将完善理论证明部分,在理论上证明H2范数的有界性假设.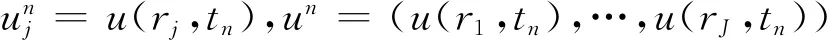
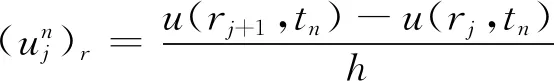

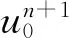
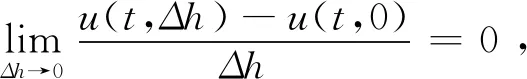
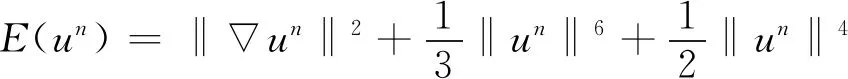
1.2 差分格式收敛性分析
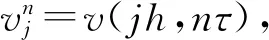
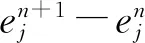
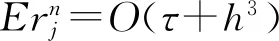
1.3 数值验证
2 数值实验
2.1 初始条件
2.2 数值观察说明
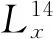
2.3 结果展示和分析

3 结论

