基于改进高频注入法的PMSM转速检测方法

陈景文，王培瑞，李英春

(陕西科技大学 电气与控制工程学院，陕西 西安 710021)

0 引言

永磁同步电机(permanent magnet synchronous machine，PMSM)因优点众多而被广泛应用.通常PMSM需机械式位置传感器检测转子位置，而机械式传感器在恶劣环境下容易失效且增加了系统成本[1].因此，有学者提出无位置传感器控制方法，在中/高速时有基于数学模型的观测器法[2]，而在零/低速时，有用信号的信噪比很低导致中/高速的观测器法失效，于是高频信号注入法应运而生[3].

高频注入法的关键在于信号注入、信号提取、位置观测三个部分.文献[4]对不同注入信号及注入方式详细叙述，并对他们的优缺点进行分析，进而对以后的发展趋势进行展望；文献[5]选用方波注入法，该方法可以将注入电压频率提高到开关频率，但噪声较明显；文献[6-8]通过对脉振注入法进行仿真与试验分析，验证了脉振注入法不依赖电机参数与工况，具有较好的鲁棒性，但带通滤波器不可避免地带来信号幅值衰减等问题.

针对此类问题，文献[9]提出卡尔曼滤波器法进行信号处理，该方法能有效减小信号的相位和幅值误差，但运算量较大；文献[10]提出一种基于滑动平均滤波器和锁相环相结合的改进信号解调算法，该方法具有更高的带宽和更好的谐波抑制能力，但该方法难以对参数进行实时修改；文献[11]提出一种基于小波变换的滤波方法，有效解决了传统滤波器提取信号精度不佳的问题，文献[12]对高频响应电流和电压进行同时解调，增加了系统的稳定性.但文献[11,12]的方法对硬件的实时采样精度有一定要求；文献[13]同时考虑直轴和交轴分量作为解调信号，该方法能够减弱估计误差，但仍使用了数字滤波器，这不可避免地影响了系统的动态稳定性；文献[14]提出一种LPF串联双频陷波器的位置误差信号提取方法，该方法虽然能够提高带宽，但带来了信号的相位延迟.

在提取出高频信号后，为获得转速信息，文献[15-17]通过龙伯格观测器获取转速并经实验验证该方法的有效性，但该方法参数整定复杂，系统在受到较大扰动时，控制器参数不一定满足要求导致系统失稳；文献[18]提出分数倍分频锁相环来估算转子位置，该方法简单易实现，但因噪声影响给系统附加了繁重的运算过程；文献[19,20]通过考虑交叉耦合项、高频载波电流的影响对系统进行了误差补偿，但没有对误差信号提取部分和解调部分进行改进.

为进一步优化提取高频信号的过程、提高提取精度和改善观测器的动态性能.本文提出一种二级广义二阶积分器来提取信号，该方法能根据转速自适应改变中心频率以获得系统的最优性能.同时，设计一种新型锁相环估算转速，以提高系统的抗扰能力.最后通过仿真和实验与传统方法进行对比，验证所提改进高频注入法的有效性.

1 脉振高频电压信号注入法

1.1 高频注入及其电流响应

在同步旋转坐标系d-q中定义高频激励下的PMSM电压方程为：

(1)

定义转子估计误差角：

(2)

则在估计转子同步旋转坐标系中，高频电压与电流的关系为：

(3)

(4)

式(4)中：ΔL=(Ld-Lq)/2,L=(Ld+Lq)/2

(5)

式(5)中：uin为高频电压信号的幅值，ωin为高频电压信号的频率.

此时，高频电流可简化为：

(6)

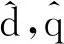
1.2 转子位置估计

(7)

如果转子位置估算误差足够小，则可以把该误差信号线性化，即：

(8)

图1 传统位置观测器结构图

2 新型转子位置观测器

2.1 信号提取部分

传统低阶数字滤波器性能不佳，高阶数字滤波器虽然能够优化提取效果但引入了一系列问题，如信号幅值衰减、相位延迟等，且数字滤波器运算复杂，参数整定困难也给实验过程带来了一定的挑战.

针对传统数字滤波器的种种问题，本文提出一种新型转子位置观测器，该观测器包括两个串联的广义二阶积分器.一级广义二阶积分器代替BPF，依据转速自适应更新中心频率以获得提取高频信号的最佳效果；二级广义二阶积分器代替LPF，通过转速自适应更新中心频率来抑制二次谐波信号以实现提取基频信号的功能.新型位置观测器结构图如图2所示.

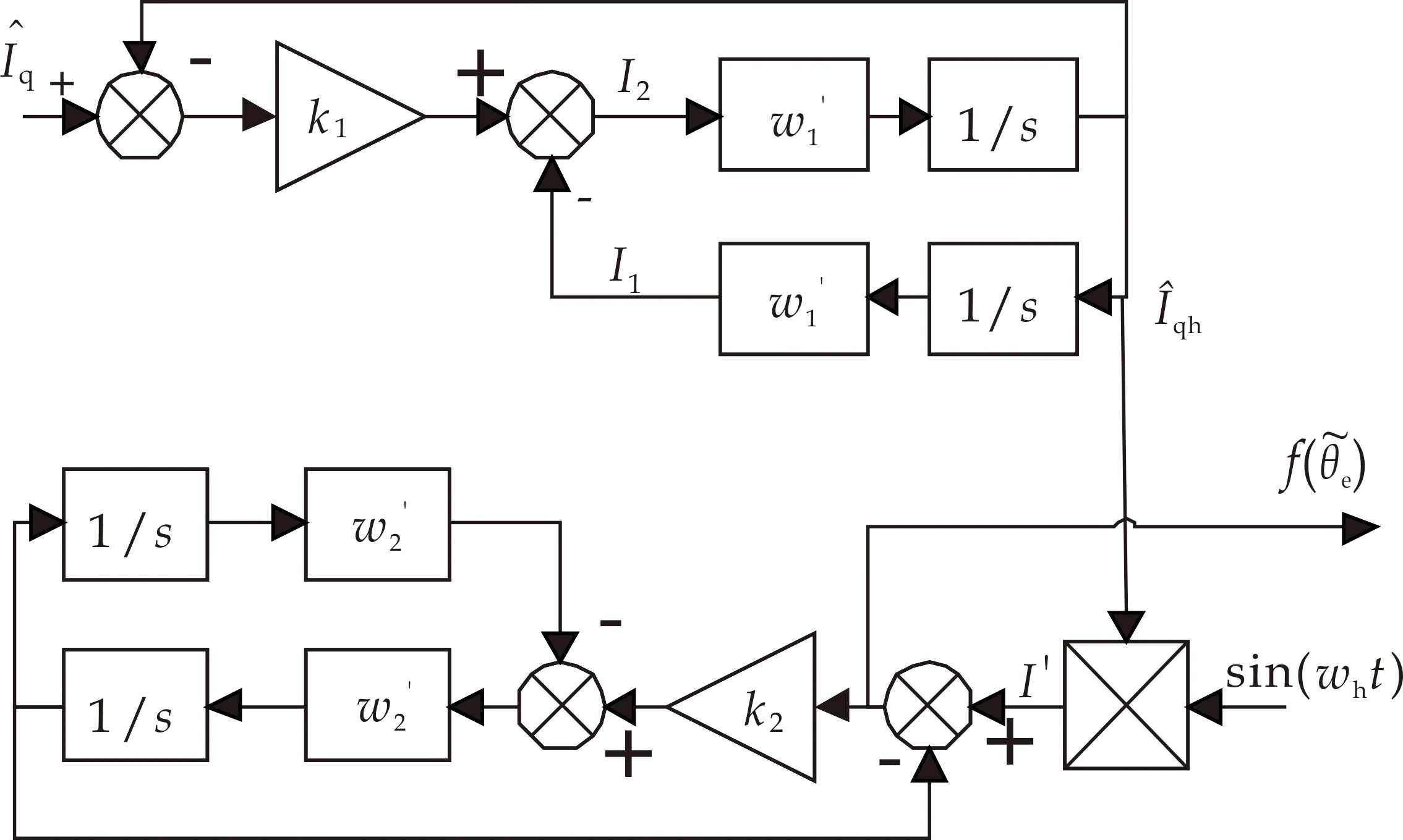
图2 信号提取模块结构图

一级结构的传递函数为：

(9)

根据一级结构传递函数特征方程，可知其二阶系统阻尼比ζ1等于k1/2.选择阻尼比ζ1为小于1的值，即为欠阻尼状态，可确保系统的快速性.k1越小，信号的提取能力越好，但会相应地减少带宽，若k1选择太小则会导致转速估计失败，为保证较好的信号提取效果，此处将k1设置为0.8.

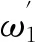
(10)

(11)

(12)

根据二级结构传递函数的特征方程，可知其二阶系统的阻尼比ζ2等于k2/2，同样选择阻尼比ζ2小于1.k2越小，提取信号的速度越快，k2越大，对特定次谐波的抑制能力越强，但过大的k2会使基波信号附加过多谐波导致转子位置估计偏差过大，为保证系统的快速性和准确性，此处将k2设置为1.

2.2 信号解调部分

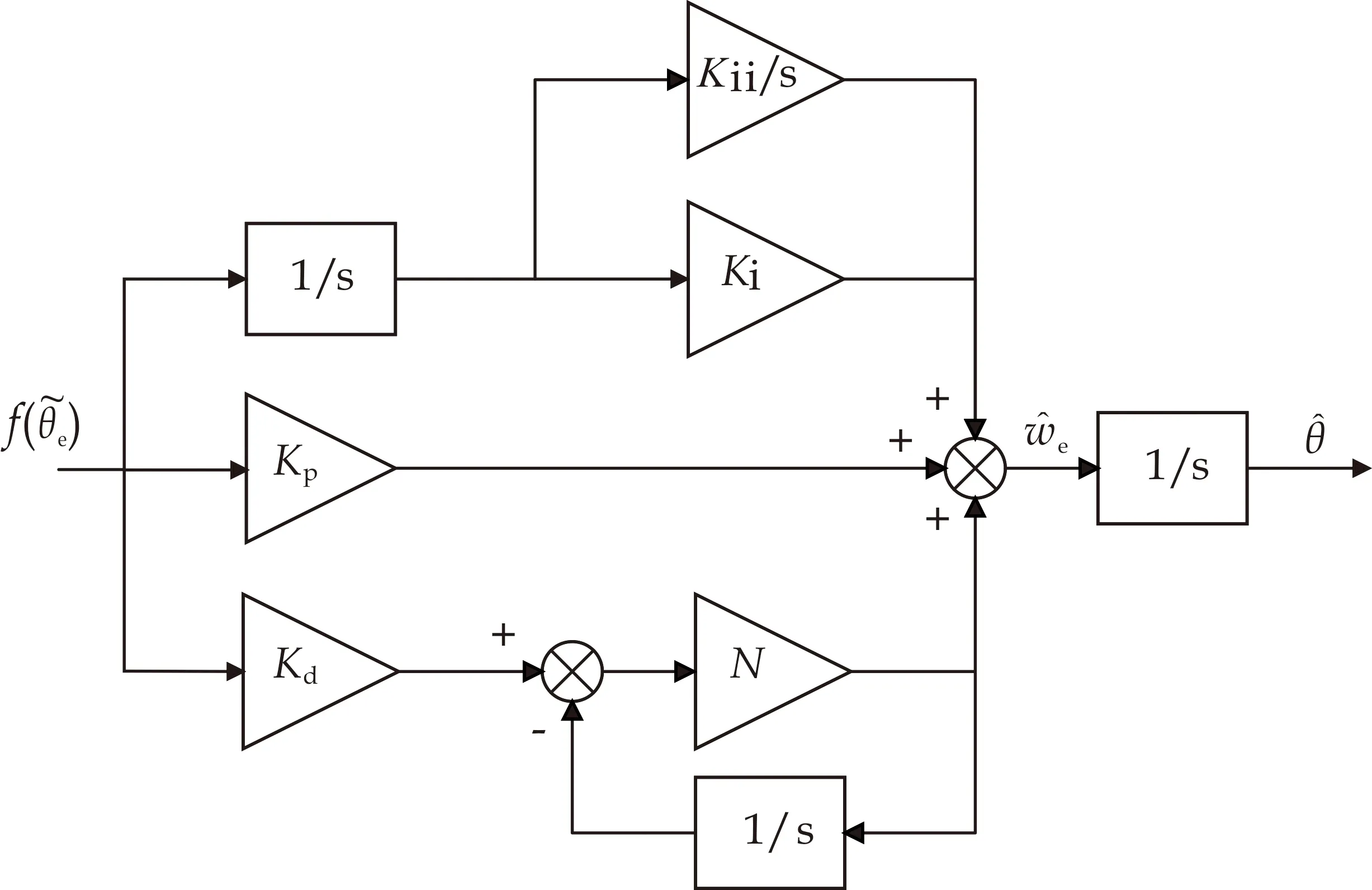
图3 信号提取模块结构图

3 仿真与实验

3.1 仿真分析

为验证所提改进高频注入法的有效性，在Simulink中进行仿真验证，系统仿真结构框图如图4所示，电机参数如表1所示，电机仿真参数与实验参数相同，电机给定转速为100 r/min.

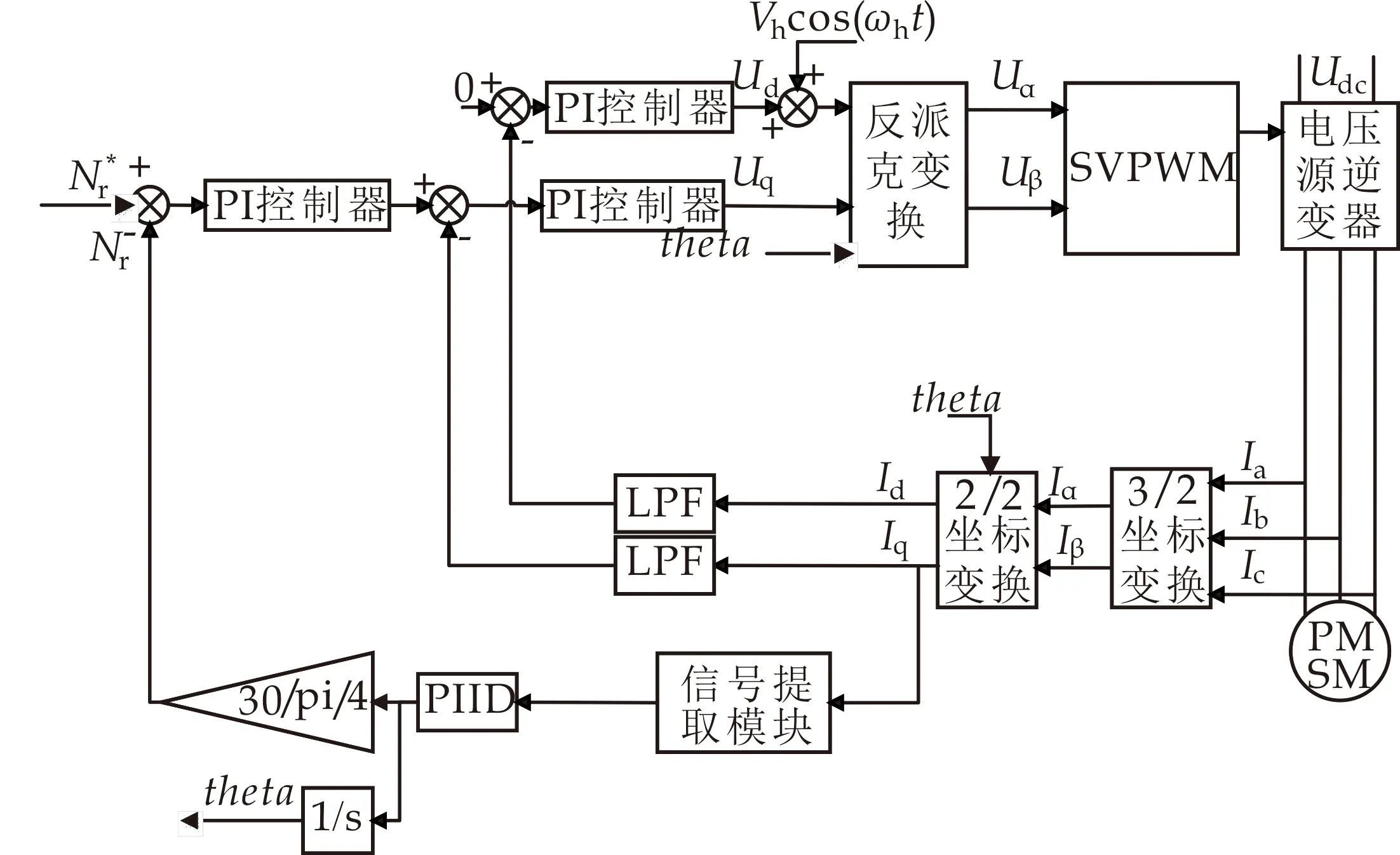
图4 系统仿真结构图

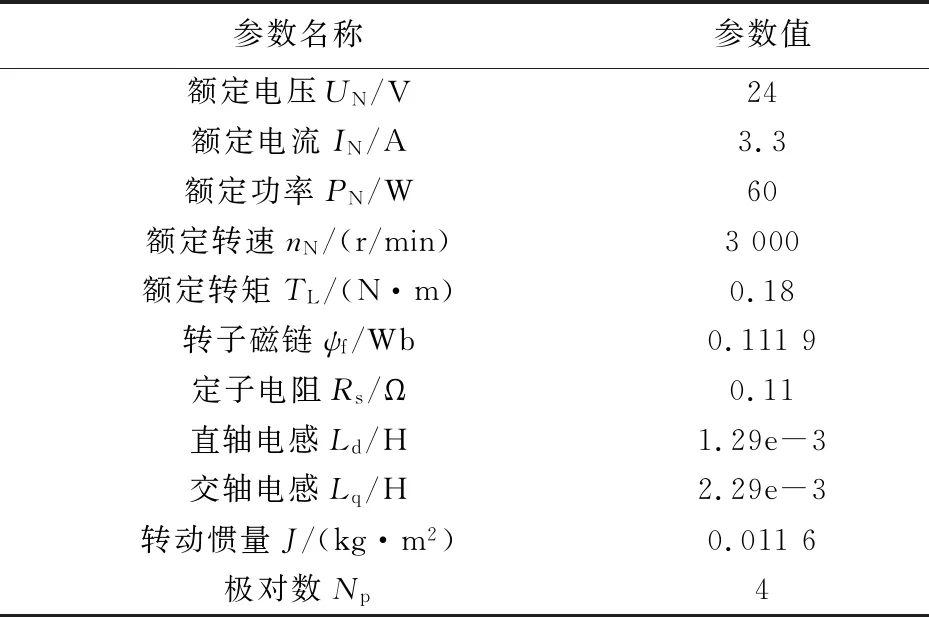
表1 电机参数

传统、改进方法的转子位置误差信号波形图如图5、图6所示.传统方法中信号波动较大时转子位置误差超过±0.15 rad，稳定时误差在±0.05 rad之间；改进方法中信号波动时转子位置误差最大为±0.04 rad，稳定时误差在±0.02 rad之间.改进方法的转子动态误差幅值仅为传统方法转子动态误差幅值的26.6%，稳态误差幅值仅为40%.可以看出改进方法提取转子位置误差信号的幅值更小，线性化更加明显，估算转子位置更趋近于实际转子位置，能够验证改进高频注入法拥有更好的信号提取效果.

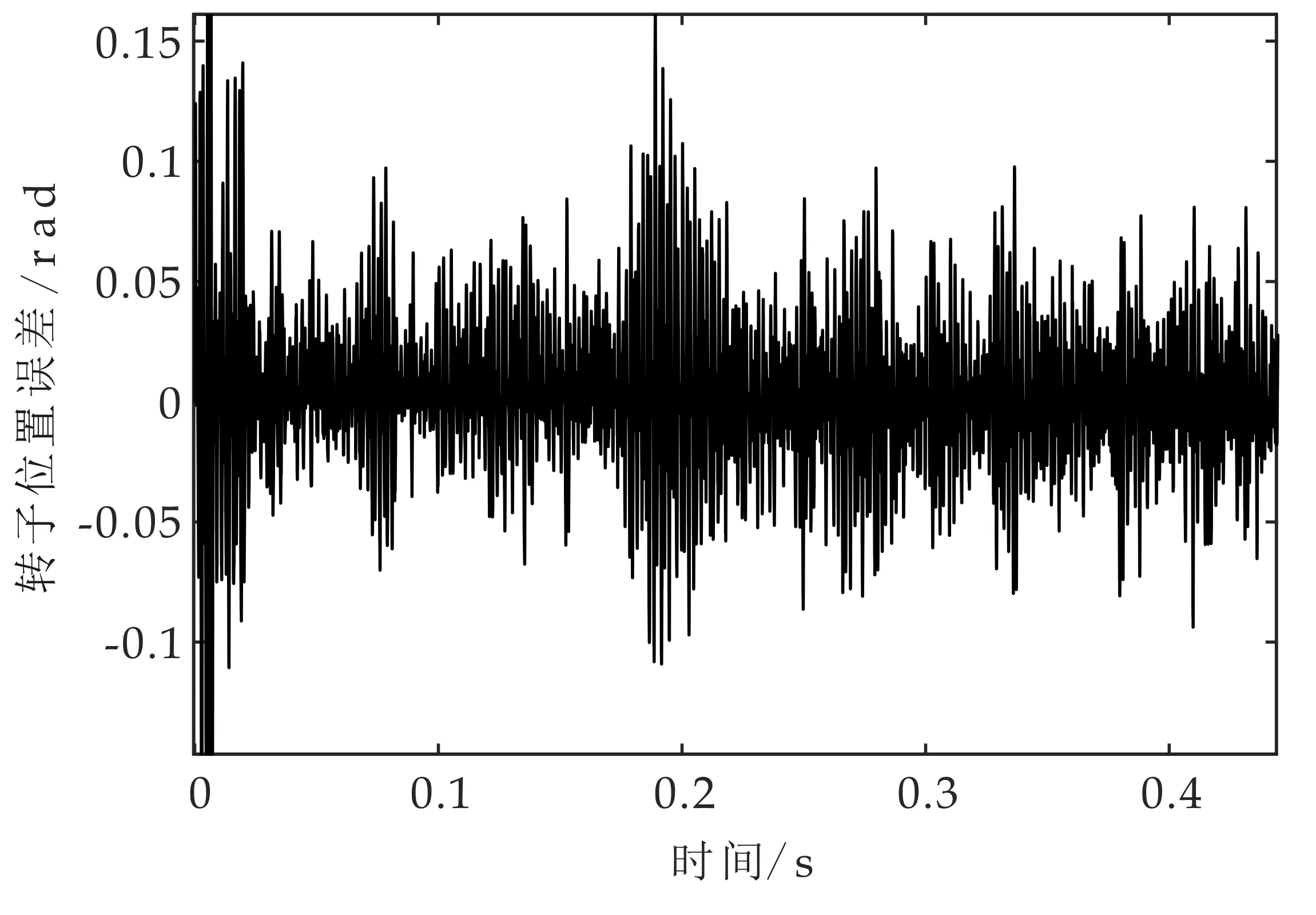
图5 空载时传统方法转子位置误差信号波形图

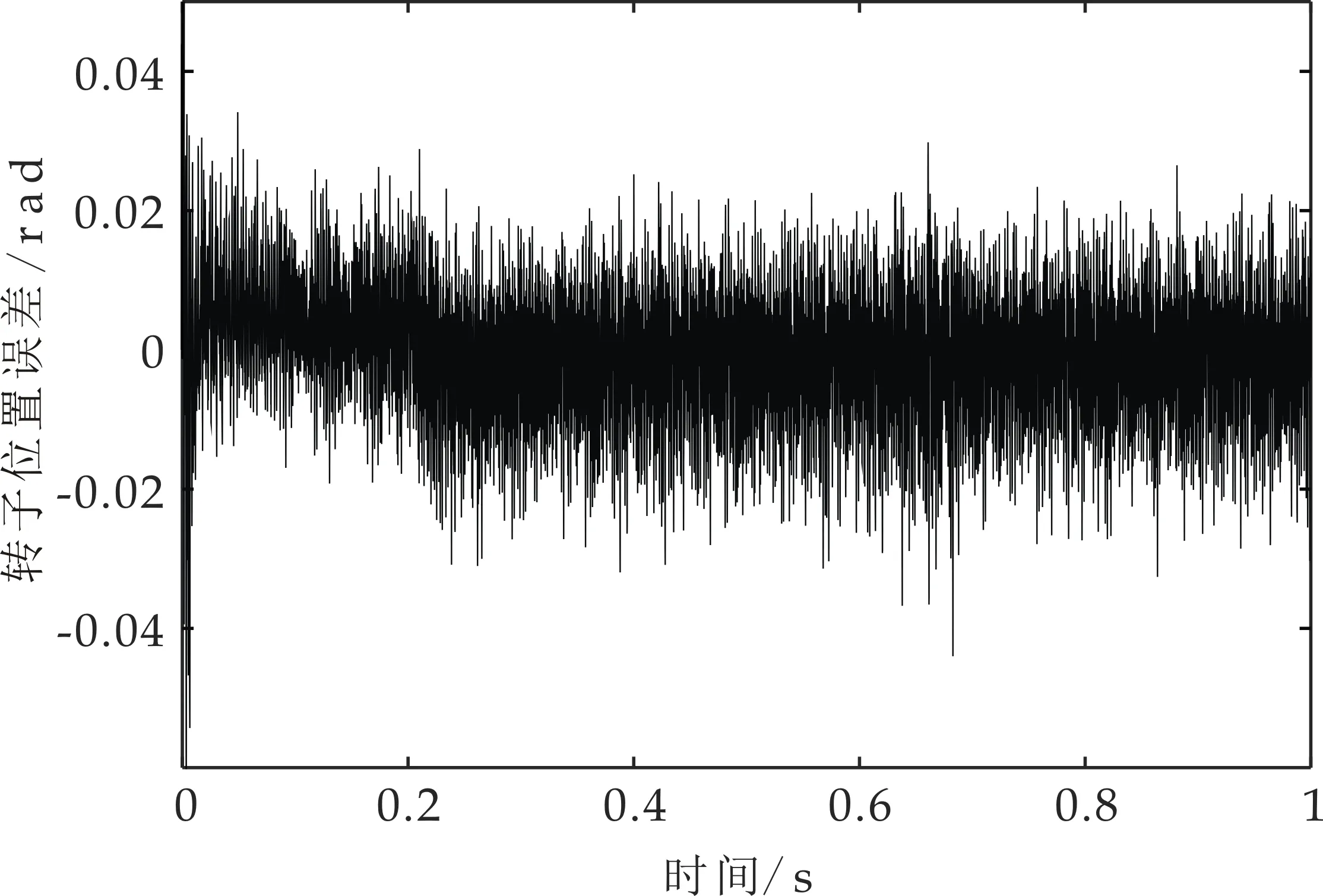
图6 空载时改进方法转子位置误差信号波形图

电机空载时，传统、改进方法的估计转速与给定转速的误差信号波形图如图7、图8所示.后续所提转速估计误差均为估计转速与给定转速的差值.传统方法中初始时刻估计误差幅值最大达12 r/min，0.2 s时误差幅值最大达到-8.2 r/min，稳定时误差幅值在±3 r/min之间；改进方法中初始时刻估计误差幅值最大达8.5 r/min，0.2 s时误差幅值最大达-7 r/min，稳定时估计误差幅值在±2.5 r/min之间.可以看出空载时改进方法的估计误差幅值比传统方法的估计误差幅值减小了16.6%，验证了改进高频注入法能够减小系统的估计误差，提高转速的估计精度.

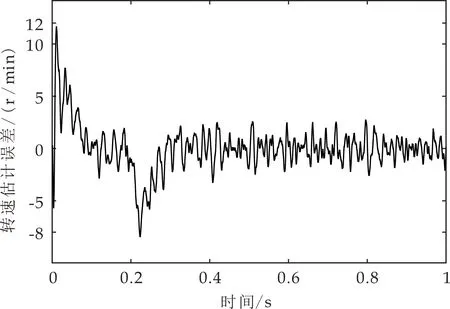
图7 空载时传统方法转速估计误差波形图

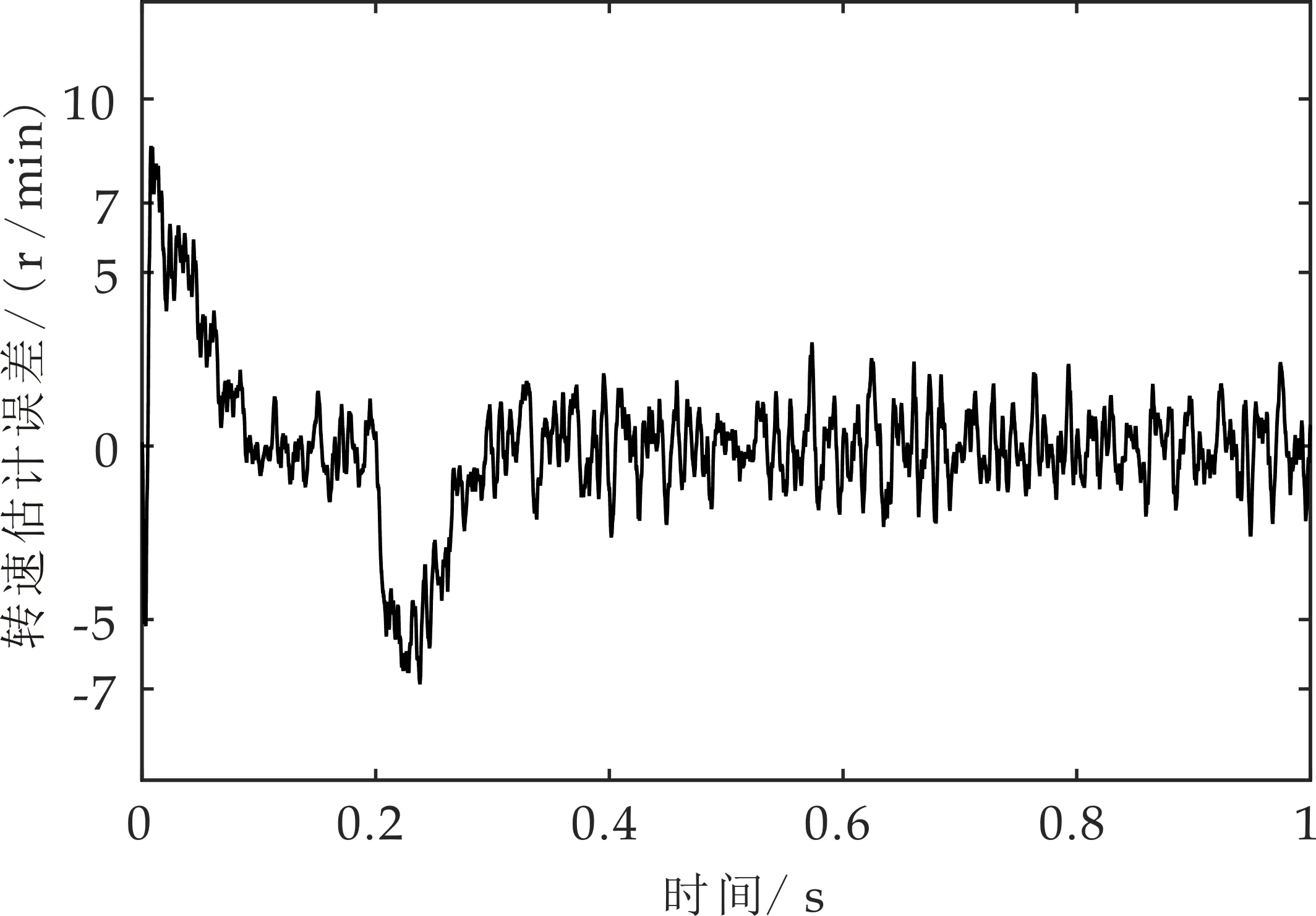
图8 空载时改进方法转速估计误差波形图

k1或k2设置不当会导致转速估计失败，图9为k1过小时，转速估计失败时转速估计误差波形图；图10为k2过大时，转速估计失败时转速估计误差波形图.

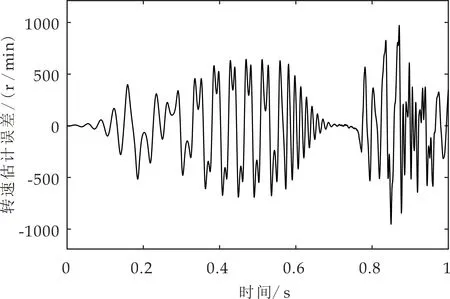
图9 k1=0.2，k2=1时的转速估计误差波形图

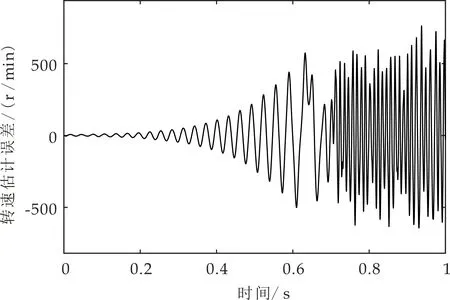
图10 k1=1，k2=5时的转速估计误差波形图

3.2 实验分析

系统硬件电路如图11所示.实验平台如图12所示，包括计算机、上位机页面、电源、示波器、STM32控制板、电机和负载等.选用JGA25-370型电机作为负载通过联轴器与PMSM相连，并通过控制程序为实验电机突加负载；STM32控制板选用STM32F446完成实验电机的FOC控制，改进广义二阶积分器，PIID控制器等程序的编写；通过上位机的发送区更新参数，改进的广义二阶积分器中k1，k2可通过上位机在线修改以达到实际运行过程中的最优效果，此处将k1设置为0.8，将k2设置为1.

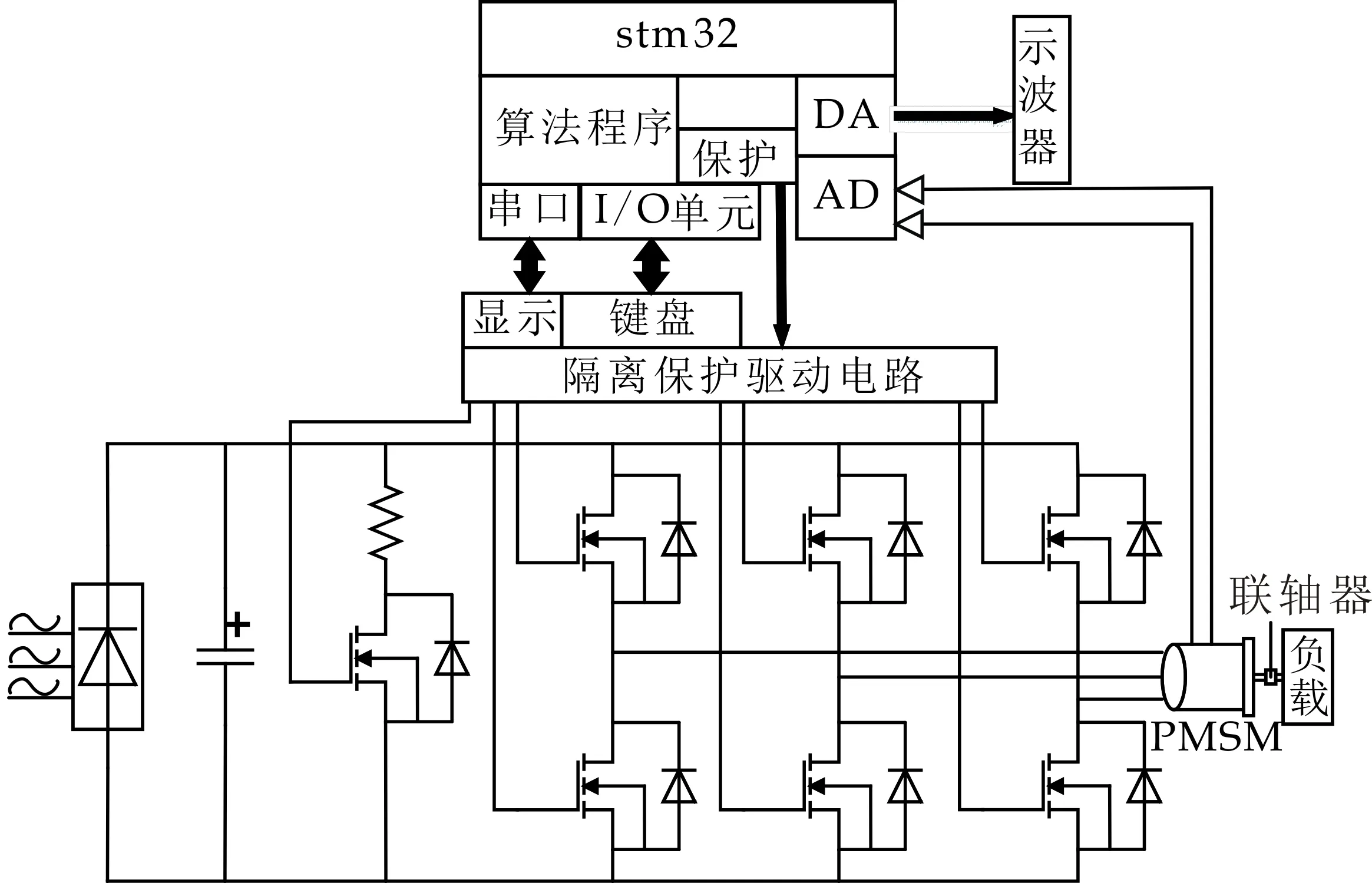
图11 硬件电路图

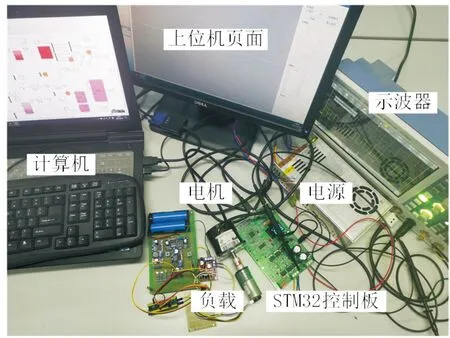
图12 实验平台

实验中逆变器开关频率选择10 kHz，注入电压幅值选择30 V，频率选择800 Hz.对于注入信号频率，一般考虑基波频率，系统带宽和开关频率的限制.若注入信号的频率超过开关频率的二分之一，会产生噪声；若注入信号的频率与基频相近，则注入信号难以与基波信号分离.一般注入信号选择0.5～2 kHz，此处选择0.8 kHz为仿真与实验效果均较好的注入频率.注入信号幅值也有一定的限制，逆变器的非线性特性、电流反馈值限制了注入信号的最小幅值；噪声需要的电能限制了注入信号的最大幅值，一般选择系统额定电压的0.1倍，此处选择30 V.

实验中在1.5 s时为系统突加2 N·m负载，传统转速波形图如图13、图14所示，改进方法转速波形图如图15、图16所示.在突加负载时系统的实际转速跌落至81 r/min，传统方法的估计转速跌落至74 r/min，改进方法的估计转速跌落至77 r/min，改进方法较传统方法的估计转速跌落减小了3 r/min，验证了改进方法的抗扰能力较强.

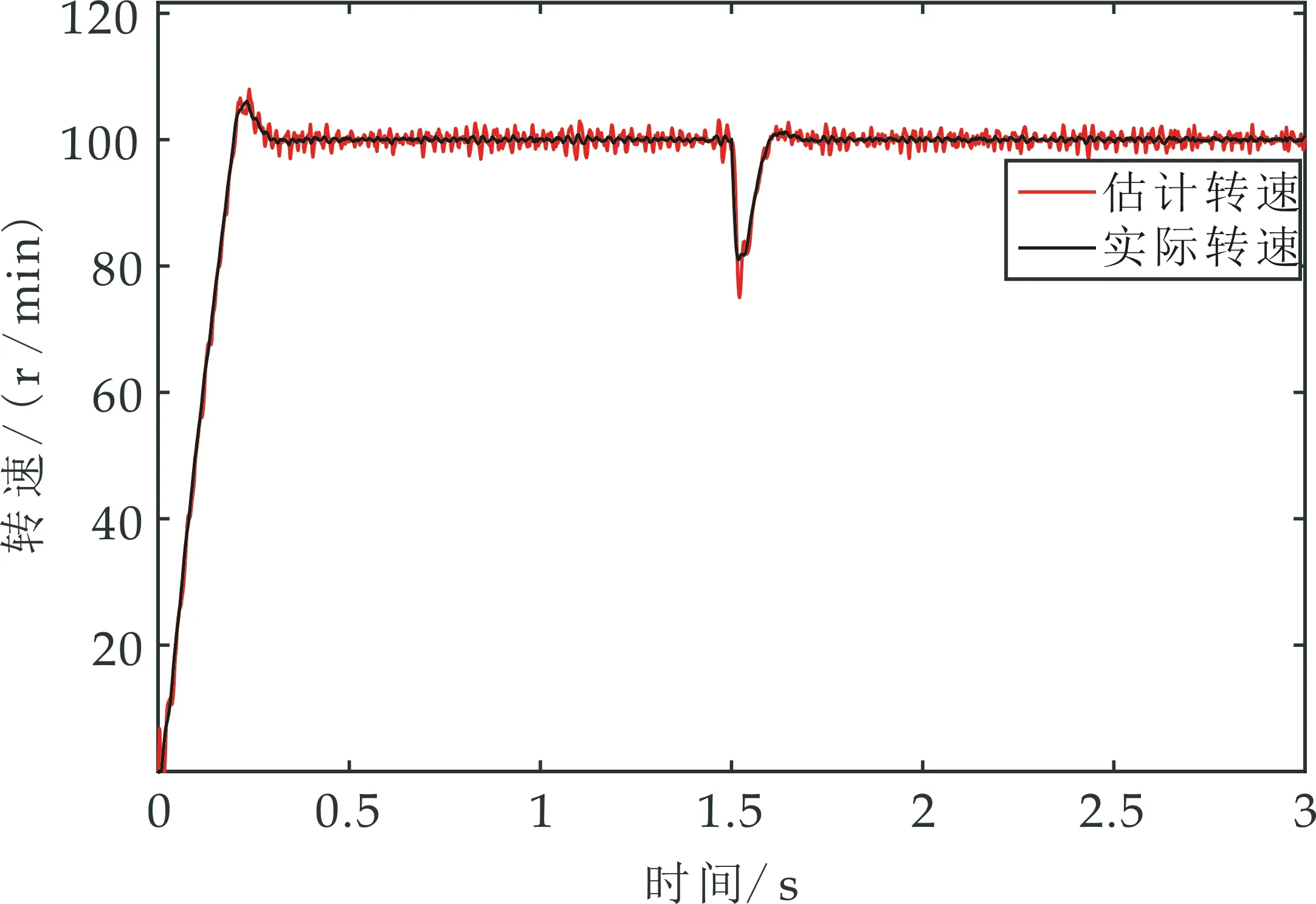
图13 突加负载时传统方法转速波形图

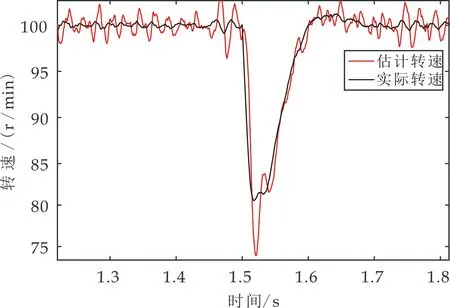
图14 突加负载时传统方法转速波形局部放大图

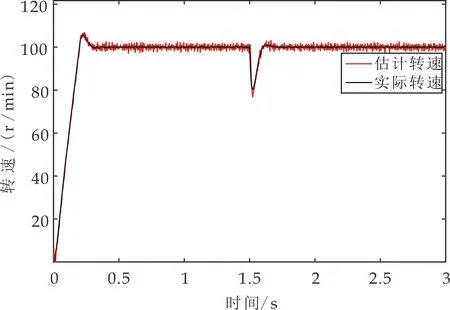
图15 突加负载时改进方法转速波形图

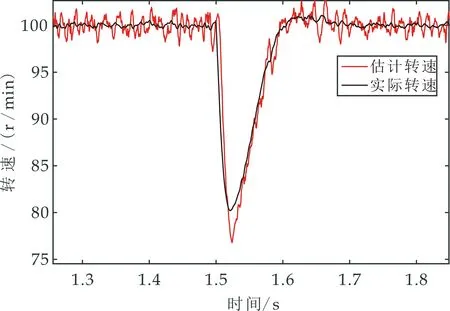
图16 突加负载时改进方法转速波形局部放大图

实验中在1.5 s时为系统突加2 N·m负载，传统、改进方法的转速估计误差波形图如图17、图18所示.传统方法的转速估计误差最大为26 r/min；改进方法的转速估计误差最大为23 r/min，相较于传统方法转速估计误差减小了11.5%左右.

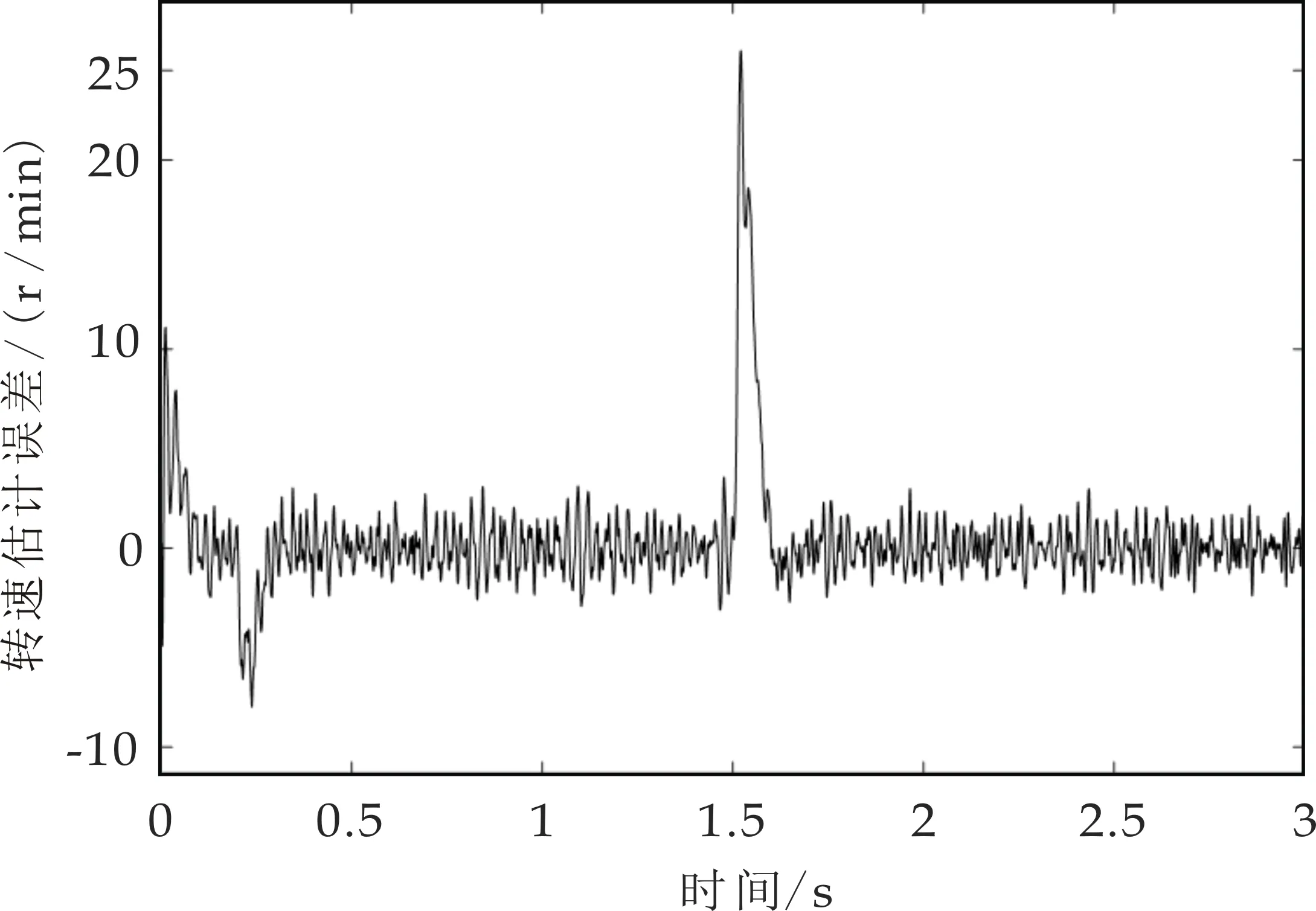
图17 突加负载时传统方法转速估计误差波形图

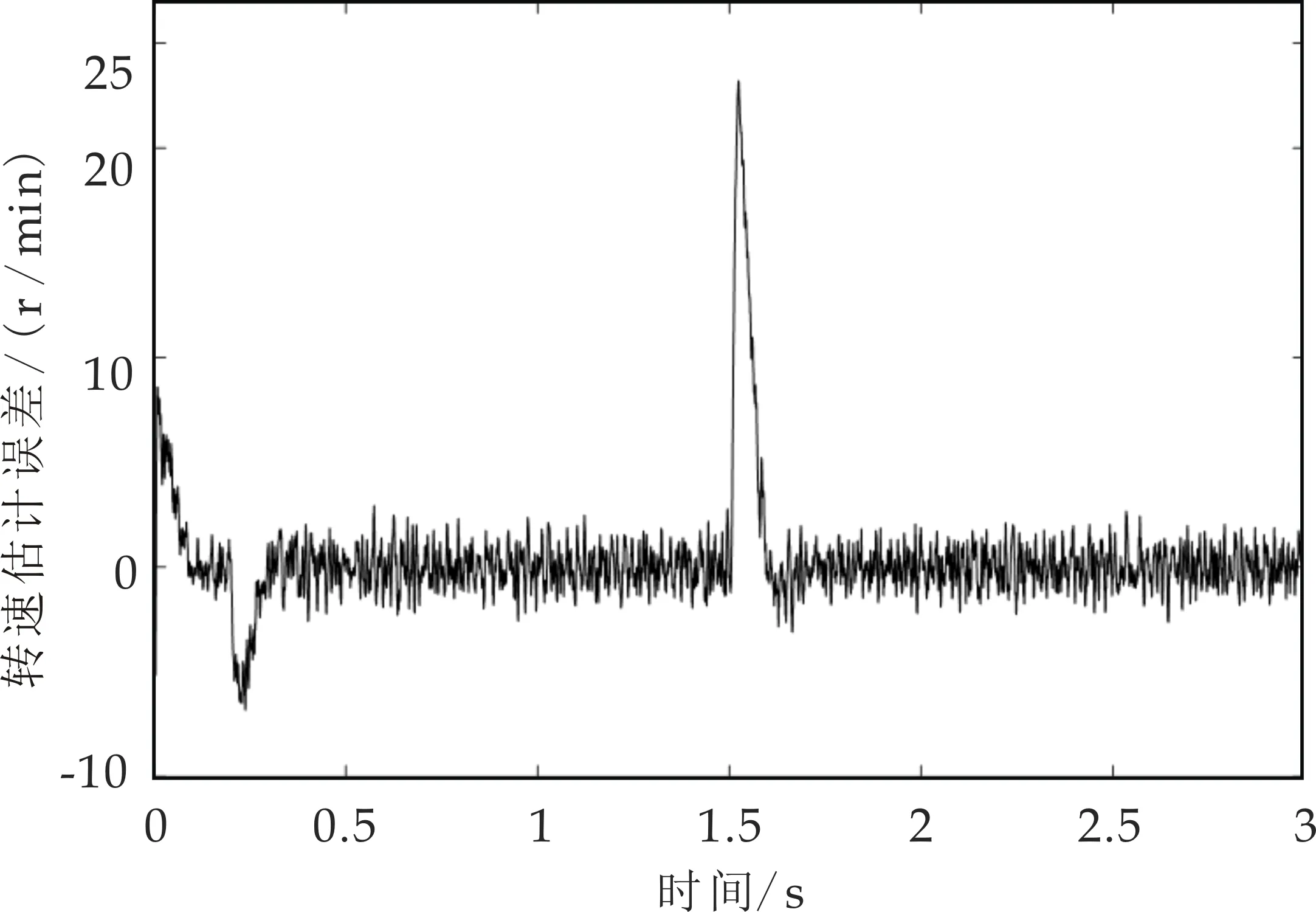
图18 突加负载时改进方法转速估计误差波形图

通过波形可以看出，当突加负载时，改进方法的转速估计误差较小，验证了改进高频注入法能够提高系统的抗扰能力，削弱转速估计误差，提高系统的控制精度和鲁棒性.

4 结论

为满足PMSM更高性能的要求，本文研究了基于改进高频注入法的PMSM转速检测方法.设计自适应二级广义二阶积分器替换带通滤波器和低通滤波器；设计PIID控制器代替信号解调过程中的PI控制器.最后，通过仿真和实验验证，本文所提方法能有效减小信号提取误差，并具有良好的动静态特性和鲁棒性