中密度纤维板平面立式铣削排屑特征的数值模拟与试验验证
孙勤杰,周曦禾,翁锦萍,李晓旭,周捍东*
(1.南京林业大学材料科学与工程学院,南京 210037; 2. 南京林业大学林业资源高效加工利用协同创新中心,南京 210037;3.国家林业和草原局北京林业机械研究所,北京 100029 )
切屑及粉尘是木质材料及产品生产加工过程中的必然产物,如不加以有效控制和处置,不仅是车间及作业环境的污染源,而且还是粉尘爆炸与火灾等事故和职业卫生健康安全的隐患源[1]。目前,家具、地板等木材加工企业虽均已采用除尘系统的吸尘罩对机床产生的切屑粉尘进行吸集,但吸集效果不甚理想,以至于影响产品质量甚至额外增加刀具维护成本[2-3],造成这一现状的根本原因是,吸尘罩这类非标准的构件设计未能针对种类繁多的切削类型与各自的排屑特征。对于设计欠合理的吸尘罩,可以通过加大其吸风量来提高吸尘罩的吸集效果,但这势必增加除尘系统的电能消耗而造成能源浪费[4]。因此,在涉尘的环保、生产安全、污染减排和职业卫生健康备受关注的背景下,针对木材切削机床种类繁多、排屑特征差异极大且排屑受切削参数影响等特点,以及吸尘罩的设计缺乏科学性这一现状,通过对刀具排屑的数值模拟,掌握排屑特征并以此作为吸尘罩优化设计的依据,从源头上解决粉尘散发造成污染这一难题,具有十分重要的现实意义和应用价值。
目前,国内外在木材切屑的形成、粉尘量及其粒径分布和机床周围粉尘散发等研究方面已有较多报道。Pfeiffer 等[5]试验研究了侧铣切屑形成机理与切屑破坏过程;Rogoziński等[6]研究了木质复合材料的CNC钻孔排屑过程所产生的粉尘量与粒径分布;Rautio等[7]建立了立式铣削产生粉尘量与平均切屑厚度关系的数学模型;曹平祥等[8]和郭晓磊等[9]采用高速摄像与图像分析方法,在不同的铣削转速下,对中密度纤维板、刨花板、杉木细木工板边部铣削的切屑流速度和扩散角变化规律进行了研究;Darmawan等[10]试验研究了立式螺旋铣刀不同螺旋角度对松木切屑流扩散角度的影响;Rudak等[11]针对刨花板立式铣削排屑方向与切屑运动速度进行了试验研究,在此基础上建立了立式铣削排屑过程的数学模型。在切削排屑气固流场研究方面, Belut等[12]通过数值模拟了机床周围颗粒运动轨迹与气流场;李小民等[13]采用了滑移网格技术和离散相模型,对封边机吸尘罩内气流场及切屑颗粒运动分布进行了数值模拟。
综上所述,目前国内外在木材切屑的产生与切屑流的研究方面,基本是在试验基础上开展的,尽管部分研究采用新的技术手段,但在切屑运动特征研究和模型的建立上依然是采用在实物测定进行的。也有学者采用数值模拟方法对封边机排屑流场开展了相关研究,但对于立式铣削排屑气固流场的模拟却鲜有报道。为此,笔者以中密度纤维板(medium density fiberboard,MDF)基材为切削对象,采用计算流体力学模拟技术,研究了立式铣削排屑场气固流动特征,以期为立式铣削和其他木材切削类型的吸尘罩优化设计提供一种高效、科学的方法。
1 研究对象与内容
本研究运用计算流体力学FLUENT仿真软件,数值模拟直径6 mm双刃柄铣刀在常用转速范围(10 000~24 000 r/min)下其周边空气流动特征、环流场气流速度及分布,以及环流最大速度与铣刀转速之间的关系。在进给速度9 m/min的条件下,模拟直径6 mm双刃柄铣刀(圆周刃前角8°、后角15°,底刃前角15°、后角20°)在中密度纤维板表面铣削沟槽(宽度6 mm、深度5 mm)的排屑气固流场,研究分析平面立式铣削的排屑特征、切屑颗粒的运动速度与空间分布规律。
2 研究方法
2.1 铣刀几何模型的建立
针对板式家具板面开槽、铣型常用的镂铣加工,选用T001型TCT直刃铣刀。采用HandyScan 300型三维激光扫描设备对铣刀进行扫描,建立铣刀三维轮廓几何模型,如图1所示。
2.2 计算域的确定与网格的划分
计算域的大小与网格疏密决定着模拟的准确性和精度,计算域的确定与网格划分对于数值模拟至关重要。基于平面立式铣削的加工特点和机床吸尘罩优化设计的目标,为掌握立式铣削刀刃处的排屑特征,模拟以长宽高240 mm×280 mm×100 mm长方体为排屑场气固流体的计算域(图2)。鉴于切削刃的复杂轮廓,计算域的网格划分采用非结构化四面体,并对切削区进行了网格局部细化加密。
2.3 排屑域气固流场数学模型
数学模型的确定是准确模拟铣刀排屑场中颗粒与气流流动规律的重要保证。据笔者对板式家具镂铣排屑量的实测与计算,计算域内两相流中气固体积浓度小于0.1,属于稀相气固流场;因而,模拟采用欧拉-拉格朗日计算模型,即在欧拉坐标系下用连续方程对气体运动进行求解,在拉格朗日坐标系下采用离散模型计算固体颗粒运动及轨迹[14]。
在保证计算准确性的前提下,本项研究对排屑场做以下简化假设:
假设1:由于空气的黏度和被加工对象材质的密度与硬度相对均较低,且柄铣刀的每刃切削量较小,以及空气对高速旋转刀具的冷却作用,因而忽略铣刀旋转过程中与空气、被切削对象之间摩擦所产生的热量[15];
假设2:考虑木业加工行业中立式铣削速度普遍较高,所产生的切屑颗粒粒径极差较小且质量较轻,同时也参考国际同行在木材切屑流仿真的实践经验[13,16],故将切屑颗粒简化为球形颗粒。
根据假设1,环流场中的空气流动服从质量守恒、动量守恒,用公式(1)~(3)3个方程进行描述。根据假设2,气流场中颗粒运动轨迹采用颗粒运动方程公式(4)进行计算[14]。
1)质量守恒方程
(1)
式中:ρ为空气密度;t为时间,xi为i方向网格单元长度;ui为i方向气流速度。
2)动量守恒方程
(2)
式中:ui和uj分别为i和j方向的气流速度;xi和xj分别为i和j方向的网格单元长度;ρ为空气密度;p为气流压力;τij为应力张量;gi为i方向的重力体积力;Fi为i方向的外部体积力以及其他模型相关源项。
3)湍流方程
立式铣削环流场是铣刀在高速旋转过程中所产生的,为非稳定的不可压缩湍流流场,因此,采用realizable k-ε湍流模型对环流场湍流进行模拟[17]。其湍动能及其耗散率输运方程为:
(3)
(4)
式中:k是环流场湍动能;ε是湍流耗散率;t是时间;uj是j方向的气流速度;μ是空气的动力黏度;μt是湍流黏性系数;xj是j方向的网格单元长度;Gk是平均速度梯度引起的湍动能;Gb是浮力影响引起的湍动能;ρ为空气密度;YM是可压缩湍流脉动膨胀耗散率的影响;C1、C2和C1ε是常数;C3ε是浮力对耗散率的影响;v是空气运动黏度系数;S是变形张量;σk、σε分别是湍动能及其耗散率的湍流普朗特常量。
4)切屑颗粒运动方程
由于切屑颗粒为离散、非连续的运动状态,因此,通过气流与颗粒之间相互作用的力平衡方程计算颗粒的运动轨迹。其计算公式如下:
(5)
式中:fD(u-up)表示气流对颗粒的曳力;gx(ρp-ρ)/ρp表示压力梯度力;t为时间;gx为重力加速度;ρ和ρp分别为空气和颗粒的密度;fx为附加质量力;u和up分别为气流、颗粒的速度。
fD的计算公式为:
(6)
式中:dp为颗粒直径;μ为空气动力黏度;CD为曳力系数;Re为雷诺数。
2.4 计算域边界条件设置
模拟以中密度纤维板(密度为850 kg/m3)为铣削对象,根据立式铣削的加工特点,计算域的四周与上表面作为流场的进出口边界,边界类型为压力,压力值为标准大气压;选取的铣削进给速度为9 m/min,产生的切屑颗粒经实测在0.1~300 μm范围并基本服从rosin-rammler分布,平均切屑产生量为3.83 g/s。
采用网格滑移的方法模拟刀具的旋转运动,以铣刀的外表面为旋转壁面,并对壁面进行壁面函数法处理。考虑空气的黏性,假设铣刀外表面与气流之间无相对滑移。
2.5 计算方法
为通过上述建立的数学模型中偏微分方程组对排屑域气固流场的气流速度、压力、颗粒运动参数等值进行计算,采用有限体积法将偏微分方程组转化为离散方程,分别采用PRESTO!压力插值方法,一阶迎风离散格式的动量、湍动能和湍流耗散率插值方法在网格节点上进行构建离散方程,并使用SIMPLIC算法对离散方程组进行计算。为保证边界条件、网格质量、数学模型选择的合理性,通过监测计算过程中的动量、质量、耗散率等残差的收敛性来判定计算结果的准确性,保证计算残差均在10-3以下[18]。为了提高流场计算速度,先使用稳态求解器计算流场至稳定状态,再通过瞬态求解器计算非稳态项,时间步长为1×10-4s。
2.6 数据提取
流场中气流和固体颗粒的运动轨迹、各点的速度大小与方向等信息均可从仿真界面上动态显示。为定量地分析排屑流场中气流与颗粒运动特征参数,运用FLUENT软件后处理模块的REPORTS功能,通过在计算域中依据需要而设置的截面,记录该截面上各点气流与颗粒的速度、方向、压力和通过该截面的颗粒数、气流量等参数,以DPM、Excel文档形式记录和导出。
2.7 试验验证
在某板式家具生产线KN-2409DE型板面开槽机上,在与模拟相同的铣削、基材和无吸尘罩的条件下,使用i-speed3型高速摄像仪(最高帧数2 000 fps),利用基材区段颜色差异的示踪原理,采集铣刀排屑视频,采用i-SPEEDViewer视频图像分析软件,获得切屑流运动方向、颗粒运动速度,在相同的铣削条件下比较颗粒的模拟速度与实测速度之间的误差。
3 结果与分析
3.1 网格确定与无关性验证
为保证模拟的准确性,满足工程应用的精度要求,同时减小计算工作量,提高模拟效率,排除网格数对模拟计算结果的影响,选用适宜的网格数是关键。为此,本项研究选用6个网格数(80万,100万,120万,150万,210万和300万),分别对立式铣削的排屑场进行了数值模拟计算,并以气流速度值作为检验指标,进行网格数与计算结果无关性的验证。提取了在同一转速、不同网格数的条件下排屑场中各点的气流速度,并比较同一点的气流速度。当速度的误差值小于3%、能够满足工程应用的要求时,则可忽略网格数对计算结果准确性产生的影响[18]。
图3是以14 000 r/min低转速、24 000 r/min高转速为例,采用6个不同的网格数进行排屑场模拟计算,通过分析在垂直于铣刀轴线平面、沿其径向的气流速度分布,检验网格数对数值模拟的无关性。表1是在所选上述6个网格数条件下,通过数据提取获得的对应的排屑场在垂直于铣刀轴线、沿其径向平面的速度最大误差。误差的比较是以网格数为80万个时流场中速度值为基准。
由图3、表1可见,对于铣刀转速为14 000和24 000 r/min,当网格数在100万个以下时,排屑场环流径向各点的气流速度均明显与其他网格数条件下的速度分布重合度不高,计算结果有较大误差,误差分别为24.8%和8.5%。当网格数大于100万个时,排屑场环流径向各点的气流速度基本一致,径向速度分布曲线基本重合,最大误差分别为3.6%和2.6%。由此可见,当转速低于14 000 r/min,适宜的网格数150万~300万;当转速高于14 000 r/min,适宜的网格数120万~300万。两种转速下气流场速度误差最小,分别为1.3%与0.8%,故网格数为150万均为最佳。
笔者认为,网格数对仿真计算精度的影响的原因:一方面是由于非结构化网格过于致密造成网格过度扭曲,从而降低了计算精度;另一方面是因网格尺度过小造成数值计算的截断误差,故本研究排屑场数值模拟选用的网格数为150万。
3.2 铣刀环流场气流速度分布
铣刀的高速旋转诱导空气在其表面形成一个环形气流场,笔者模拟分析了转速为10 000和24 000 r/min铣刀环流场速度分别情况。图4是铣刀转速在24 000 r/min条件下环流速度矢量图,图5a、b分别是环流横截面速度矢量图和环流径向速度分布。
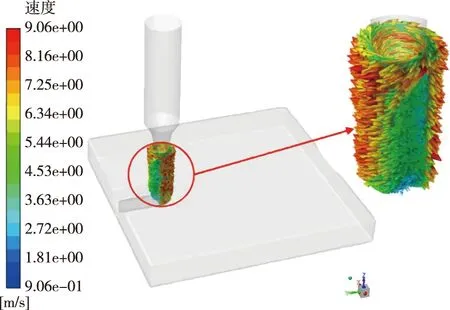
图4 环流场气流速度矢量图(铣刀转速24 000 r/min)Fig. 4 Diagram of vector velocity in annular airflow field (milling speed of 24 000 r/min)
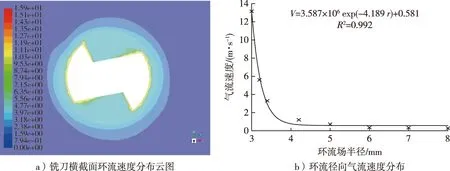
图5 环流场气流速度分布图(铣刀转速24 000 r/min)Fig. 5 Diagram of air velocity distribution in annular airflow field (milling speed of 24 000 r/min)
由图4可见,在铣刀切削刃外围存在一个与铣刀同轴、旋转同向的环流气流场。从图5可见,环流场的外径为16~40 mm,环流场外径为铣刀直径的2.7~6.7倍。在切削刃表面存在一层极薄的黏性底层[19-20],环流最大速度为15.72 m/s,位于切削刃圆附近,环流层内气流速度随其半径的增加呈指数函数关系降低。
图6是铣刀转速分别为10 000,12 000,14 000,16 000,18 000,20 000,22 000和24 000 r/min 条件下,环流场气流的最大速度、平均速度和铣削速度分布。
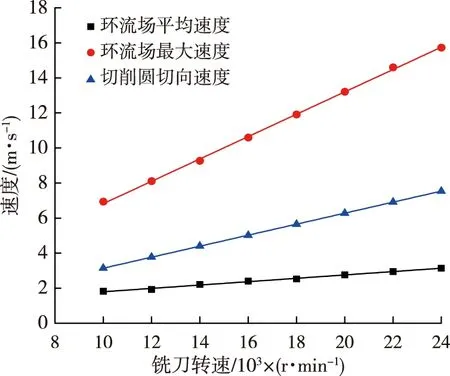
图6 铣刀在不同转速下环流场最大与平均气流速度Fig. 6 Maximum and average air velocity in annular airflow field at different milling speeds
由图6可见,铣刀环形流场中最大和平均气流速度均随着铣刀转速的增高呈线性增大,铣刀转速由10 000 r/min升高至24 000 r/min,最大速度由6.93 m/s上升到15.72 m/s,平均速度由1.82 m/s增加为3.14 m/s。由图中数据可发现,位于切削圆处的最大气流速度均大于相同铣刀转速下切削刃口的切削速度。笔者分析这是由于立式铣刀的结构所致,随着铣刀的高速旋转,双刃铣刀刀片以一定的前角强制刀具排屑槽内空气作圆周运动,在离心力的作用下被甩向四周,这一作用有助于刀具的排屑和冷却。
3.3 立式铣削排屑特征
为解决平面立式铣削作业环境粉尘污染的难题,准确掌握其排屑特征是提高吸尘罩吸尘效果的重要依据。笔者针对板件家具表面铣削沟槽加工,在上述6个不同铣刀转速下,模拟了直径6 mm双刃柄铣刀在无约束空间的排屑情况。图7是转速在24 000 r/min下模拟得到铣刀排屑切屑颗粒的分布与运动情况。

图7 立式铣削排屑情况(铣刀转速24 000 r/min)Fig. 7 The situation of chip removal in vertical milling (milling speed of 24 000 r/min)
由图7可见,切屑颗粒在铣刀的撞击下获得动能并被强制排出切削区,排屑主要集中在两个区域,即主排屑区和次排屑区。主排屑区是以切削区为顶点的椭圆状锥体,切屑颗粒在水平锥角为83°~86°、垂直锥角为20°~22°的锥体内向外抛射。在主排屑区内,排屑由密集流和稀疏流两部分构成。呈柱状的密集流中以较为粗大颗粒为主,颗粒以17.85 m/s的初始速度沿沟槽轮廓表面喷射,抛射方向与进给方向之间呈14.5°夹角。在密集流喷射的过程中,切屑中粒径细小、质量较小的颗粒沿着柱状密集流的轴线以8.22 m/s的速度呈散射状的稀疏流形式发散。在环流的曳力牵引下,占颗粒数4%~6%细微颗粒由切削区和稀疏流扩散至次排屑区(图8)。
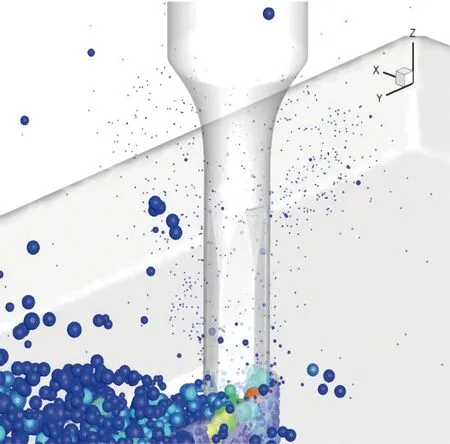
图8 次排屑区细微颗粒物分布情况(铣刀转速24 000 r/min)Fig. 8 Distribution of fine particulate matter in secondary chip discharge area (milling speed of 24 000 r/min)
3.4 切屑颗粒速度分布
利用吸尘罩吸集切屑是加工机床粉尘污染源头控制的重要途径,因此排屑气固流场中切屑颗粒的速度是吸尘罩结构优化与气流组织的重要依据。图9和图10分别是铣刀为10 000,12 000,14 000,16 000,18 000,20 000,22 000和24 000 r/min 转速下,通过模拟获得的主排屑区密集流和稀疏流中切屑颗粒的平均速度分布情况。
由图9可以看出,在主排屑区的密集流中,切屑颗粒由切削区排出的初始速度与铣刀转速呈正相关函数关系,当转速由10 000 r/min提高至24 000 r/min时,颗粒的初始速度由7.57 m/s 升高至17.85 m/s。在某一铣刀转速下,密集流中颗粒的速度随喷射距离的增加呈线性降低。以24 000 r/min铣刀转速为例,当切屑颗粒的初始速度为17.85 m/s,沿着柱状轨迹喷射至10倍的铣刀直径处时,颗粒的速度降至6.63 m/s,仅为初始速度的37%。
由图10可见,在主排屑区稀疏流中,细小颗粒的初始速度和沿铣刀径向喷散距离的速度程度衰减与密集流具有相同的规律。以24 000 r/min铣刀转速为例,颗粒在切削区排出的初始速度为8.22 m/s,喷散至10倍铣刀直径处时,速度降至1.40 m/s,仅为初始速度的17%。图9和图10显示,切屑颗粒喷射和发散至10倍铣刀直径处,密集流和稀疏流中颗粒的速度衰减程度不同。
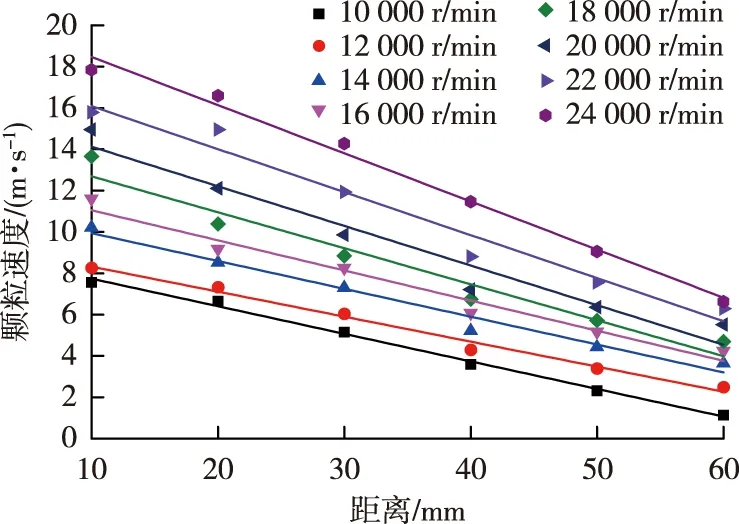
图9 不同铣刀转速下主排屑区密集流颗粒平均速度Fig. 9 Average velocity of dense particles in the main chip discharge area at six milling cutter rotation speeds
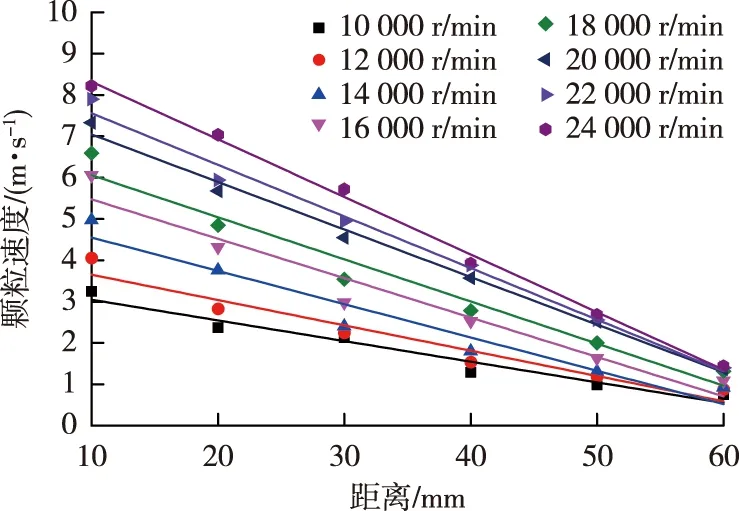
图10 不同铣刀转速下主排屑区稀疏流颗粒平均速度Fig. 10 Average particle velocities of sparse flow in the main chip discharge area at six milling cutter rotation speeds
3.5 试验验证
在上述6个不同铣刀转速下,通过视频图像分析了排屑方向与颗粒分布、密集流与稀疏流颗粒速度变化等特征。试验表明,铣削的排屑分布和颗粒分布与模拟相吻合;密集流颗粒初始速度和10倍铣刀直径处速度的实测与模拟误差分别为3.5%~7.1%和3.3%~6.7%,稀疏流颗粒初始速度和10倍铣刀直径处速度的实测与模拟误差分别为3.2%~5.6%和3.1%~4.6%,误差值与铣刀转速呈正相关(表2)。
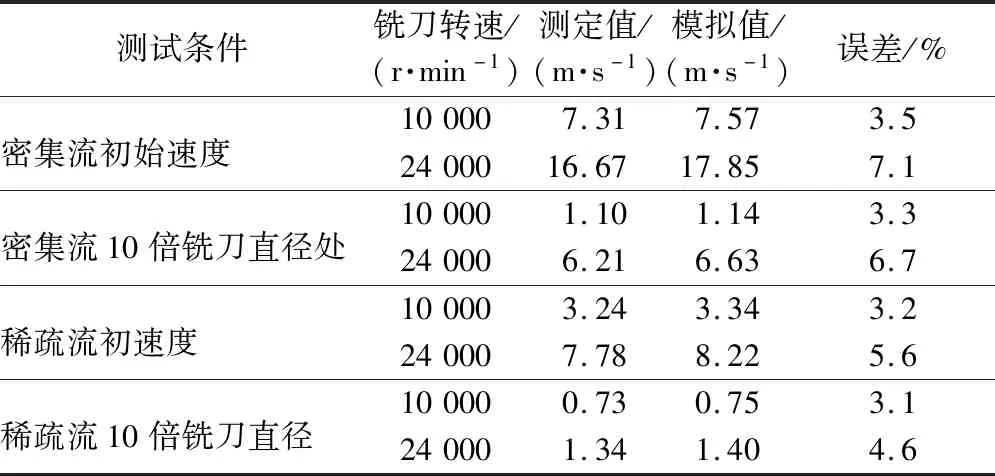
表2 颗粒运动速度测定值与模拟值对比Table 2 The comparison between the measured and simulated velocities of the particle
4 结 论
1)沿立式铣刀轴向存在一个与铣刀同向的旋转环形气流场,最大切向速度位于铣刀切削圆外层附近,随环流半径增大呈指数减小。铣刀转速在10 000~24 000 r/min范围,环形气流场的直径为铣刀直径的2.7~6.7倍,最大切向速度为6.93~15.72 m/s,并与铣刀转速呈正相关函数关系。
2)平面立式铣削以主排屑区和次排屑区为排屑特征,主排屑区是以切削区为顶点的椭圆状锥体,铣削速度在10 000~24 000 r/min范围,切屑在水平锥角为83°~86°、垂直锥角为20°~22°的范围内抛射和发散;次排屑区位于环流的外部。
3)主排屑区的排屑由密集流和稀疏流两部分构成,铣削速度在10 000~24 000 r/min范围内,密集流和稀疏流中颗粒的初始速度与铣刀转速呈正相关函数关系,分别在7.57~17.85 和3.34~8.22 m/s范围;密集流和稀疏流中颗粒的速度随喷射与发散距离的增加呈线性降低,沿着颗粒运动路径,距切削区10倍铣刀直径处密集流和稀疏流的颗粒分别在1.14~6.63和0.75~1.40 m/s范围。
4)通过立式铣床排屑的试验测定,排屑的方向、颗粒分布等特征与模拟相吻合;密集流和稀疏流的颗粒初始速度及10倍铣刀直径处速度的实测与模拟误差为3.1%~7.1%。

