弹性垫层温频变特性对减振型CRTSⅢ板式无砟轨道振动响应影响研究

牛振宇，刘林芽，秦佳良，左志远

（华东交通大学铁路环境振动与噪声教育部工程研究中心，江西南昌，330013）

高速铁路效率高、能耗低、运量大的特点决定了其将在未来交通运输部门中将起到重要的作用，但高速铁路技术在迅速发展的同时，振动和噪声问题未得到有效解决。针对这一问题，我国高速铁路研究者在城市轨道减振降噪经验的基础上研发了减振型CRTSⅢ板式无砟轨道，并取得了显著的减振降噪效果[1]。在该类型轨道结构中，通过布置弹性垫层来达到减振的目的。弹性垫层包括扣件胶垫层和减振垫层。扣件胶垫层与减振垫层是该类型轨道结构中具有弹性和阻尼性能的部件，它们的动态力学性能对车辆-轨道耦合系统振动响应有重要的影响。弹性垫层由黏弹性橡胶高分子材料制成，高分子材料的动力学行为往往随环境温度以及加载频率的变化呈非线性变化，同时表现出黏性液体和弹性固体的力学特征即黏弹性力学特征[2-3]。用于描述橡胶高分子材料的动力特性最基本的2 种模型为Maxwell 模型和K-V 模型[4-5]。这2 种模型均属于标准机械模型，简单直观，但由于其导数阶数均为整数，模型不能反映加载历史的影响，从而难以准确描述橡胶高分子材料的频变特性。分数阶导数模型是在标准机械模型的基础上发展而来的，其导数阶数为分数，因此，该模型能够考虑加载历史的影响，可以准确描述橡胶材料的频变特性[6-7]。赵永玲等[8]对橡胶材料频变特性进行了研究，发现分数阶K-V 模型在描述橡胶材料频变特性上存在一定的误差，而高阶分数阶导数FVMP 模型能较好地描述橡胶材料的频变特性。刘林芽等[9]利用高阶分数阶导数FVMP模型对扣件动参数进行拟合，拟合结果显示FVMP 模型计算的动参数结果与试验结果吻合较好。相比于仅有1个导数阶数的低阶分数阶导数模型，高阶分数阶导数模型在中低频和高频范围内均能描述弹性垫层的频变特性，FVMP模型是高阶分数阶导数模型中常用的一种[10]。在车辆-轨道耦合系统的分析中，通常将弹性垫层简化为线性弹簧和黏性阻尼并联的K-V 模型，但K-V 模型不能真实反映弹性垫层的频变特性[11-12]。ZHU 等[13-14]将描述扣件胶垫频变特性的分数阶K-V 模型应用于车辆-轨道耦合系统动力学模型，分析了扣件胶垫的频变特性对轮轨系统动态响应的影响。WEI等[15]对不同参考温度下分数阶K-V 模型的参数进行了拟合，对使用分数阶K-V 模型代替扣件胶垫的车辆-轨道耦合系统动力学模型进行计算，分析了扣件胶垫的温频变特性对车辆-轨道耦合系统振动响应的影响。上述文献用于表征扣件胶垫频变特性的模型在描述频变特性时存在一定程度的误差，尤其在描述中高频段内的频变特性存在较大的误差。现有文献对于减振垫层的研究一般仍采用K-V模型来替代，考虑减振垫层的温频变特性的文献较少，同时考虑扣件胶垫和减振垫层的温频变特性对轨道结构的影响的文献更少。

鉴于此，本文作者以减振型CRTSⅢ板式无砟轨道扣件胶垫与减振垫层为研究对象，通过动态力学性能试验结合温频等效原理得到弹性垫层温频变力学特性，并采用能在较宽加载频率范围内描述弹性垫层频变力学特性的高阶分数阶导数FVMP模型来建立弹性垫层的数学模型，将其嵌入车辆-轨道垂向耦合模型中，最终计算出轨道结构各部分的振动响应，从而研究弹性垫层温频变特性对轨道结构振动响应的影响。

1 弹性垫层动态力学性能试验

采用橡胶材料动态力学分析仪（dynamic thermomechanical analysis,DMA），以减振型CRTSⅢ板式无砟轨道使用的扣件胶垫和减振垫层为试验对象，在加载频率为2 Hz、不同试验温度下进行温度扫描试验，从而获取弹性垫层动参数的温度谱，如图1和图2所示。

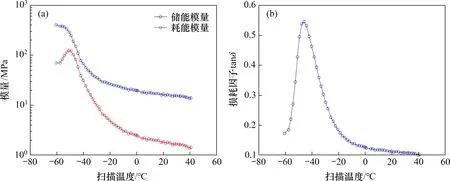
图1 扣件胶垫DMA试验值Fig.1 DMA test values of rail pad

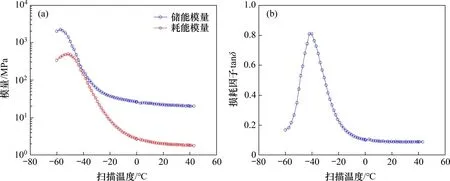
图2 减振垫层DMA试验值Fig.2 DMA test values of damping layer

2 弹性垫层FVMP模型

弹性垫层采用高阶分数阶导数FVMP 模型，如图3所示。

图3 弹性垫层FVMP模型Fig.3 FVMP model of elastic layer

FVMP模型能够用7个参数在较宽的加载频率范围内准确描述弹性垫层动参数的频变特性，其时域本构方程为

式中：Fa（t）为弹性垫层弹性力；X（t）为弹性垫层位移；μ1和μ2为FVMP模型的弹性系数；η1和η2为FVMP模型的黏性系数；Dα，Dβ和Dγ为分数阶微分算子；α，β和γ为分数阶导数阶数。

对式（1）进行Fourier 变换后经整理可得到FVMP模型确定的复模量：

式中：E*(iω)为复模量；σ(ω)和ε(ω)分别为弹性垫层正应力与正应变；i 为虚数单位。将iγ=代入式（2），分离实部与虚部并计算得到FVMP模型的储能模量Es、耗能模量El和损耗因子δ：

利用弹性垫层DMA 试验结果并基于温频等效原理[16]可转化为不同参考温度点下弹性垫层动参数随加载频率变化的频变曲线，并对比K-V 模型与FVMP 模型的试验结果，如图4和图5所示。结合式（3）～（5），利用最小二乘法及遗传算法对FVMP 模型参数进行识别[9]。表1所示为40，20和-40 ℃这3 个参考温度下的频变曲线及预测结果，由此可确定高阶分数阶导数FVMP 模型的参数。

表1 弹性垫层FVMP模型参数Table 1 FVMP model parameters of elastic layer

由图4与图5可知：对于弹性垫层储能模量，在K-V 模型下显示其为不随温度和加载频率变化的常数，与试验值相比显然存在较大的偏差，而FVMP模型则能很好地对弹性垫层储能模量进行拟合；对于弹性垫层损耗因子，在K-V 模型下显示其随频率呈线性变化，但各温度下其试验值随频率并非呈严格的线性变化，而FVMP 模型对于各参考温度下损耗因子随频率的变化则可以较好地拟合。由此可知，弹性垫层的动参数与温度和加载频率有明显的相关性，相比于加载频率，温度对弹性垫层动参数的影响更为显著，但在大多数的车辆-轨道耦合模型仿真计算中，常将弹性垫层动参数看作不随温度和加载频率变化的常数，这显然是不合理的，并且相对于低阶分数阶导数模型，高阶分数阶导数FVMP 模型在高频条件下计算的动参数与试验数据吻合度更高，这是由于本模型具有3个分数阶导数阶数，能够精确描述弹性垫层动参数的频变特性。

图4 扣件胶垫FVMP模型、K-V模型预测值与试验值对比Fig.4 Comparisons of FVMP model,K-V model prediction value and test value of rail pad

图5 减振垫层FVMP模型、K-V模型预测值与试验值对比Fig.5 Comparisons of FVMP model,K-V model prediction value and test value of damping layer

3 车辆-轨道垂向耦合振动响应计算分析

采用我国CRH380 型高速客车与减振型CRTSⅢ型板式无砟轨道结构，首先建立车辆-轨道垂向耦合动力学模型，如图6所示，其中钢轨与轨道板以及自密实混凝土和底座板之间的联结都选用高阶分数阶导数FVMP 模型，然后，将弹性垫层高阶分数阶导数FVMP 模型应用于所建立的垂向耦合模型中，从而对后续弹性垫层温频变特性对轨道结构振动响应影响进行计算和分析。

3.1 车辆模型

车辆系统采用半车车辆模型，此模型考虑的车体运动状态有车体的沉浮自由度Zc及其点头自由度θc，2个转向架的沉浮自由度Zt1和Zt2及其点头自由度θt1和θt2，还有4个车轮的垂向位移Zw1，Zw2，Zw3和Zw4，共10 个自由度。车辆系统振动微分方程为

式中：Mu，Cu和Ku分别为车辆系统的质量、阻尼和刚度矩阵；Z为车辆系统的位移矢量；Pu为轮轨作用力。

3.2 轨道模型

轨道子模型采用减振型CRTSⅢ型板式无砟轨道模型，如图6所示。钢轨采用离散点支撑欧拉梁模型，为了进行数值分析，采取Ritz法将振动微分方程转化为二阶常微分方程，下式即为钢轨振型坐标二阶常微分方程组的基本形式[17]：

图6 车辆-轨道垂向耦合模型Fig.6 Model of vertical vehicle-track coupled

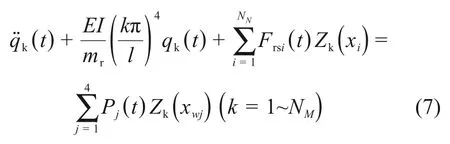
式中：qk（t）为钢轨在t时刻k阶模态空间下的位移；E和I分别为钢轨弹性模量和截面惯性矩；mr为钢轨单位长度质量；Frsi（t）为第i个扣件支点反力；NM为钢轨所截取的模态数；Pj为第j位轮对的轮轨作用力；xwj和xi分别为第j位轮对和第i个扣件沿线路的纵向坐标；Zk（xi）为钢轨垂向振型坐标函数；l为钢轨计算长度；NN为钢轨计算长度内扣件个数。

轨道板与自密实混凝土考虑为同一参数的模型，模型采用自由欧拉梁模型由减振垫层支撑。基础采用路基形式。同样采用Ritz法将其变换成二阶常微分方程，最终可以得到轨道板的垂向振动微分方程为[17]

式中：ms为轨道板质量；Tn·g(t)为第g块轨道板在t时刻k阶模态空间下的位移；βn为自由梁正交函数系内的常数；Fd（t）为减振垫层支反力；EsIs表示轨道板的抗弯刚度；Xsn（x）为自由梁正交函数系；xi∈[（g-1）L，gLs]；n0为单块轨道板上的扣件支点个数；S为轨道板所选取的广义坐标个数；Lb为底座板长度；Ls为轨道板长度，轨道板可以分Lb/Ls段。

3.3 高阶分数阶导数FVMP模型的应用

在传统的车辆-轨道垂向耦合模型中（图6），弹性垫层常使用线性K-V 模型，该传统模型下的扣件支反力与减振垫层支反力分别为：

式中：Zr（xi,t）与Zs（x,t）分别为第i个扣件对应的钢轨和轨道板位移；K与C分别为扣件胶垫的刚度系数与阻尼系数；Ks和Cs分别为轨道板下减振垫层沿长度方向的分布刚度和分布阻尼。

式（1）为本文高阶分数阶导数FVMP 模型的时域本构表达式，对式（1）进行数值求解，采用Grunwald-Letnikov 定义[18]，分别对按照分数导数定义展开。展开后将其代入式（1），进行移项、合并同类项化简，即可得到本文所使用的高阶分数阶导数FVMP 模型所对应的扣件支反力和减振垫层支反力的表达式：

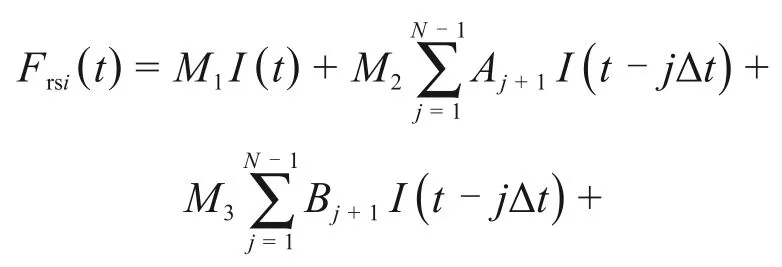
式中：I（t）为t时刻扣件胶垫的位移；N为t时刻之前的积分步数；Aj+1，Bj+1，Cj+1和Dj+1为扣件胶垫FVMP 模型的Grünwald 系数。M1，M2，M3，M4，M5和M6分别为：

减振垫层支反力Fd(t)为

式中：U（t）为t时刻减振垫层的位移；Ej+1，Fj+1，Gj+1和Hj+1为减振垫层FVMP模型的Grünwald系数；K1，K2，K3，K4，K5和K6表达式与扣件支反力表达式相同。

式（11）和式（12）中代表扣件胶垫位移的I（t）与代表减振垫层位移的U（t）可分别替换为代表钢轨位移量的Zr（xi,t）和代表轨道板位移量的Zs（x,t）。将式（11）与式（12）分别代入式（7）和式（8）可得到扣件胶垫和减振垫层使用FVMP 模型的钢轨与轨道板振型坐标二阶常微分方程组的表达式：

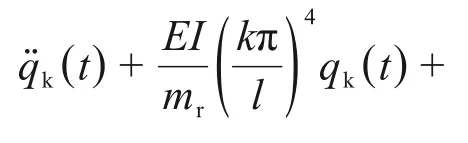
进行同样的替换,可得到减振垫层使用FVMP模型的轨道板振型坐标二阶常微分方程组的表达式如下：

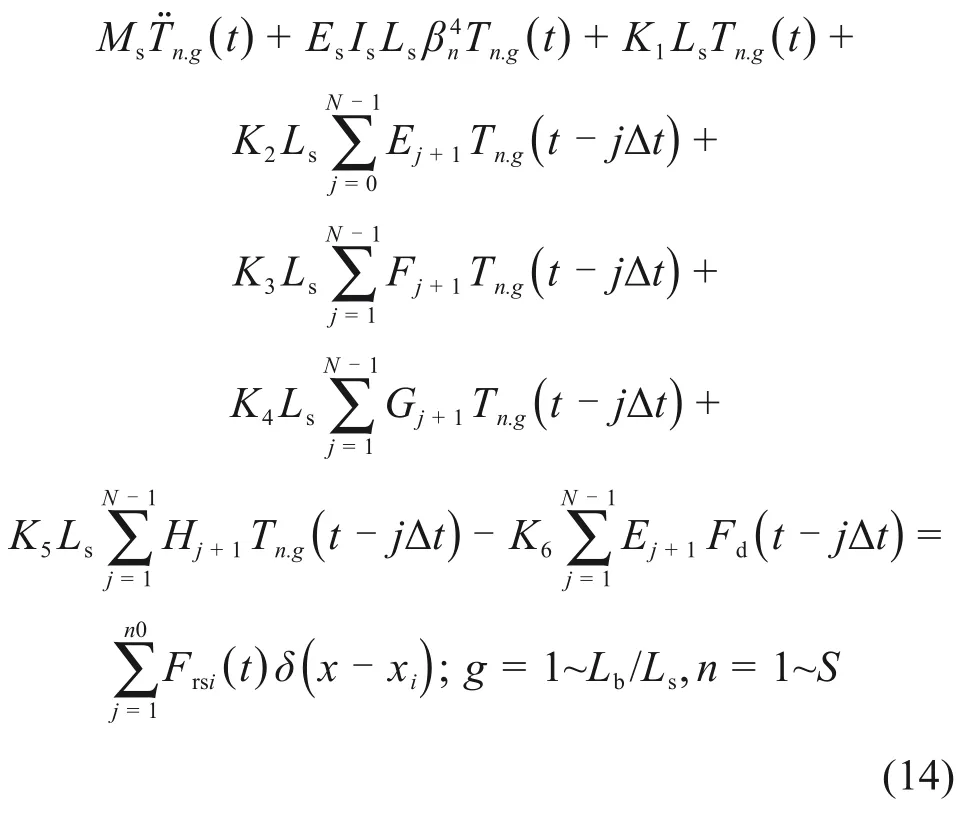
3.4 数值积分方法

车辆系统与轨道系统的相互耦合应用Hertz 非线性弹性接触理论来确定轮轨之间的垂向作用力。由此可得到弹性垫层应用高阶分数阶导数FVMP模型的车辆-轨道垂向耦合模型。各个子系统的振动方程矩阵形式如下：

式中：M，C和K分别为车辆-板式无砟轨道耦合系统的质量矩阵、阻尼矩阵和刚度矩阵；X，˙，和P分别为车辆-轨道垂向耦合模型的广义位移矢量、广义速度矢量、广义加速度矢量和广义力矢量。

对于求解该大型非线性运动微分方程组，本文采用新型显示积分法求解[17]。

式中：ψ和φ为积分常数，当ψ=φ=1/2 时，显式积分法具有较强的稳定性和较高的精度；Δt为积分时间步长，本文取1×10-4s；下标n-1，n和n+1分别为第n-1，n和n+1个子步；初始条件设为X0=V0=A0=0。

在时域分析中，式（11）与式（12）考虑了分数阶算子的非局部空间特性，即在计算每一个积分时刻由高分数阶导数FVMP 模型提供的部分扣件支反力和减振垫层支反力时，均需要考虑过去所有时刻弹性垫板的位移。Grünwald 系数是严格递减的，最后趋于零，这表明位移响应历史对当前时刻分数阶算子的影响随积分步数增大而减小。因此，在计算分数阶算子时只需要离当前时刻较近的位移。SPANOS等[19]指出，在计算分数导数算子时，只需要考虑当前时间步之前160步即可得到满意的结果，本文N取160。

3.5 轨道结构振动响应计算分析流程图

综上所述，为了更清晰地表达轨道结构振动响应的计算分析过程，设计轨道结构振动响应的计算分析流程，如图7所示。

图7 轨道结构振动响应计算分析流程图Fig.7 Flow chart of vibration response analysis and calculation of track structure

4 弹性垫层温频变特性对轨道结构振动响应的分析

4.1 计算参数

车辆及轨道结构计算参数分别如表2和表3所示，其中弹性垫层选择在温度为20 ℃、加载频率为4 Hz 下的刚度系数和阻尼系数作为K-V 模型的动参数，弹性垫层温频变参数如表1所示。

表2 CRH380高速客车的参数Table 2 Parameters of CRH380 vehicle

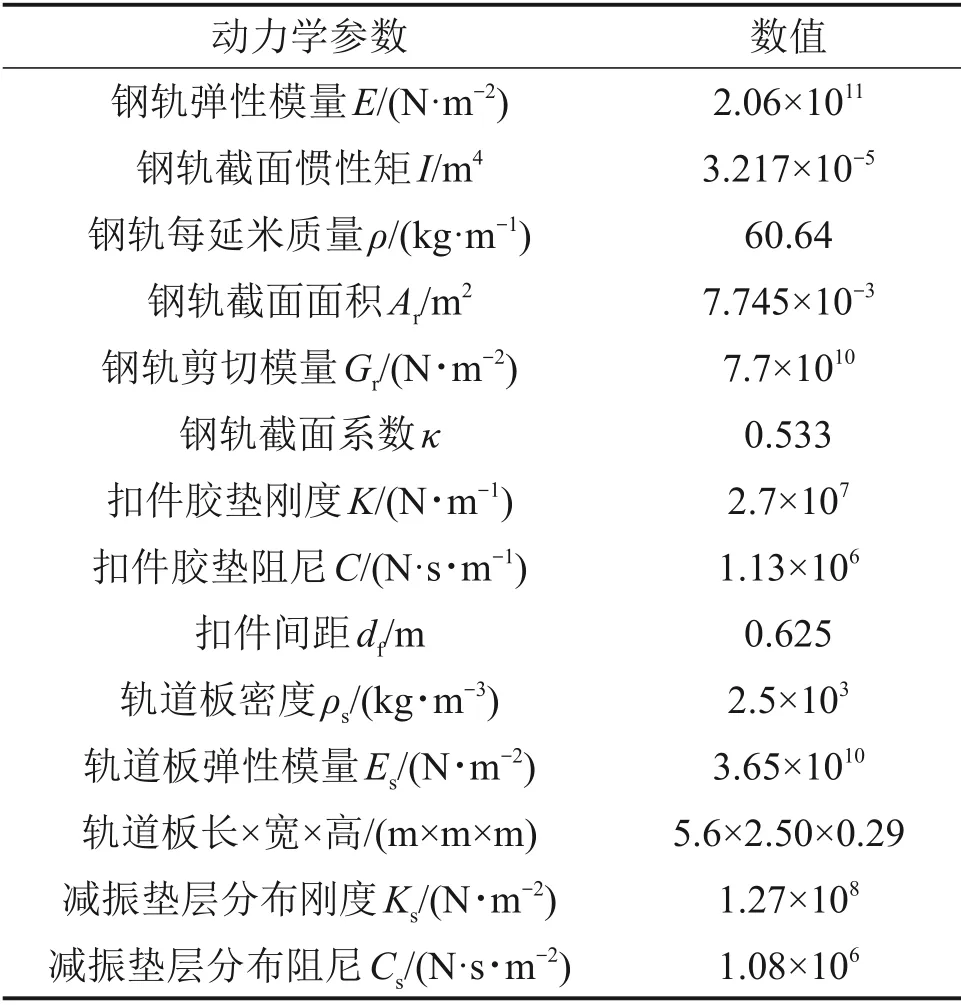
表3 减振型CRTSⅢ型板式无砟轨道参数Table 3 Parameters of vibration reducing CRTSⅢslab ballastless track

4.2 弹性垫层温频变特性对轨道结构振动响应的分析

以我国高速铁路无砟轨道不平顺谱作为轮轨系统输入激励[20]，行车速度设为350 km/h。为了研究弹性垫层温频变特性对轨道结构振动响应的影响，本文进行了4 种工况的设计，见表4，其中工况1的弹性垫层为K-V模型，即不考虑弹性垫层温变和频变特性的线性模型，将工况1与工况3进行对比是为了分析弹性垫层频变特性对轨道结构振动响应的影响，将工况2、工况3 与工况4 进行对比则是在工况3考虑弹性垫层频变特性的基础上分析弹性垫层在各参考温度点下温变特性对轨道结构振动响应的影响。

表4 弹性垫层4种工况Table 4 Four working conditions of elastic layer

时域响应中4种工况的对比如图8所示。由图8可知：在时域响应中，FVMP模型在20 ℃下的轮轨力、钢轨垂向位移、钢轨垂向振动加速度和轨道板垂向振动加速度的响应相比于K-V 模型20 ℃时的响应都呈现增加的趋势，其各峰值分别相差8.32%，16.11%，35.65%和131.06%，可见分数导数黏弹性效应能明显增大轮轨间相互作用以及轨道结构的振动响应；在各参考温度下，FVMP模型轮轨力的响应呈现出随温度降低而增大的趋势，相比于40 ℃的响应，20 ℃和-40 ℃时的响应分别增大0.3%与3.5%；FVMP 模型在各参考温度下钢轨垂向位移的响应呈现出随温度降低而减小的趋势，相比于40 ℃的响应，20 ℃和-40 ℃时的响应分别减小5.92%与37.16%，究其原因在于弹性垫层的刚度随温度降低而增大，从而导致低温下的位移响应较小；钢轨和轨道板垂向振动加速度的响应都呈现出FVMP 模型在40 ℃和-40 ℃时的响应比20 ℃时的响应大的规律，对于钢轨垂向振动加速度，40 ℃和-40℃时的响应比20 ℃时的响应分别增大1.06%与3.82%；轨道板垂向振动加速度分别增大4.8%与54.02%。

图8 轮轨力、钢轨和轨道板温频变时域响应对比图Fig.8 Comparison diagrams of time domain response of wheel-rail force,rail and slab track with temperature-and frequency-dependent

频域响应中4 种工况的对比见图9。由图9可知：对于垂向轮轨力，在低频1～40 Hz 内，FVMP模型在20 ℃时的频域响应与K-V模型20 ℃时的频域响应基本一致，但由于弹性垫层非线性动力学模型中的非线性与分数导数黏弹性效应，在40～100 Hz以及500 Hz之后，FVMP模型在20 ℃时的响应比K-V 模型20 ℃时的响应大，而在100～500 Hz的频段内则相反；FVMP 模型各参考温度在低频1～40 Hz 内基本一致，在40～350 Hz 内，FVMP 模型-40 ℃时的响应比40 ℃和20 ℃时的响应大，在500 Hz 以后则表现为40 ℃和20 ℃时的响应比-40 ℃时的响应大。

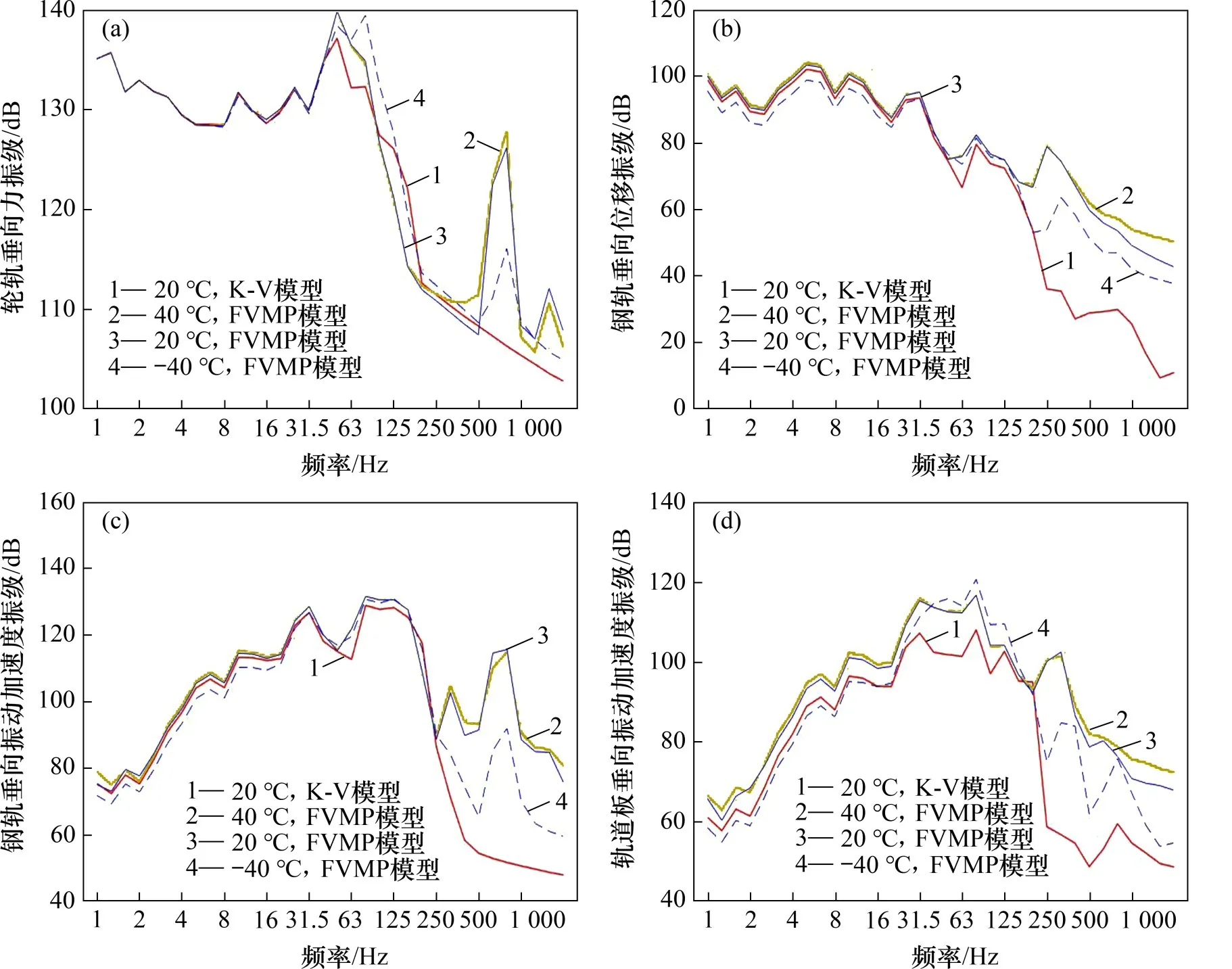
图9 轮轨力、钢轨和轨道板温频变频域响应对比图Fig.9 Comparison diagrams of frequency domain response of wheel-rail force,rail and slab track with temperature-and frequency-dependent

钢轨垂向位移频域响应在低频（1～170 Hz）段FVMP模型在20 ℃时的频域响应与K-V模型20 ℃时的频域响应差别较小，而在170 Hz 以后的频段内则表现为FVMP 模型20 ℃时的响应明显比K-V模型20 ℃时的响应大，如在1 000 Hz 时频域响应增大了23.58 dB；FVMP 模型各参考温度在1～170 Hz 内的响应差别较小，而在170 Hz 之后的响应表现为随温度降低而减小的趋势，在高频段内尤为明显，如在1 000 Hz时，FVMP模型在40，20和-40 ℃时的频域响应分别为53.96，49.16 和42.14 dB。

在全频段内，FVMP 模型在20 ℃时的频域响应比K-V 模型在20 ℃时的频域响应大，其中在250 Hz 后尤为明显，如在800 Hz 时增大了64.08 dB；FVMP模型各参考温度在1～250 Hz的频域响应差别较小，在250～500 Hz 以及1 000 Hz 之后的响应表现为随温度降低而减小的趋势，如在1 250 Hz时，FVMP模型在40，20和-40 ℃时的频域响应分别为86.25，84.98和63.37 dB。

轨道板垂向振动加速度频域响应变化与钢轨加速度的变化类似，在全频段内，FVMP 模型在20 ℃时的频域响应比K-V模型20 ℃时的频域响应大，其中在230 Hz 之后尤为明显，如在400 Hz 时增大了31.93 dB；FVMP 模型各参考温度在40～230 Hz 内表现为-40 ℃时的频域响应比40 ℃和20 ℃时的响应大；在1～40 Hz 以及315 Hz 之后的频域响应表现为随温度降低而减小的趋势，在中高频段内更为明显，如在500 Hz 时，FVMP 模型在40，20 和-40 ℃时的频域响应分别为81.94，78.65和61.84 dB。

以上对钢轨垂向位移、钢轨垂向振动加速度和轨道板垂向振动加速度频域响应分析中，在中高频段内基本上都表现为FVMP 模型在20 ℃时的响应比K-V 模型在20 ℃时的响应大，这是由于K-V 模型20 ℃工况下在高频段内过高估计了弹性垫层的阻尼，使其计算得到的振动响应比FVMP模型计算的结果小；而FVMP模型在3个参考温度点下振动响应基本表现为随参考温度降低而减小，这是由于弹性垫层的阻尼随温度降低而增大，从而导致低温下轨道结构的振动响应较小。根据以上各个轨道结构振动响应的分析，并考虑弹性垫层温频变特性相比于不考虑时有很大的差异，为提高对轨道结构预测的准确性，在进行仿真分析时，有必要考虑弹性垫层的温频变特性。

5 结论

1）弹性垫层的动参数对加载频率和温度有明显的依赖性，而高阶分数阶导数FVMP 模型能在较宽的频段内准确地描述弹性垫层的这种力学行为。

2）考虑弹性垫层的温频变特性对轨道结构垂向振动响应有较大的影响，在时域响应中，轮轨力、钢轨位移、钢轨和轨道板的加速度在FVMP模型下计算的峰值明显比K-V 模型下的峰值大；FVMP模型在各参考温度点下钢轨垂向位移的响应呈现出随温度降低而减小的趋势，而轮轨力则呈现出随温度降低而增大的趋势。

3）弹性垫层的温频变特性对轨道结构振动响应的影响集中于中高频段内，该频段内轨道结构各部分都表现为FVMP 模型下的响应比K-V 模型下的响应大；FVMP模型在该频段内的轨道结构各部分的频域响应呈现出随温度降低而减小的趋势。

4）若忽略弹性垫层的温频变特性，则会对轨道结构振动响应的预测产生很大的偏差，因此，在进行仿真分析时，为提高对轨道结构预测的准确性，有必要考虑弹性垫层的温频变特性。