烧结余热竖罐热工参数影响解析研究

张晟，赵亮，冯军胜，董辉

（1.东北大学冶金学院，辽宁沈阳，110819；2.安徽建筑大学环境与能源工程学院，安徽合肥，230601）

烧结矿生产过程中会产生大量的余热资源，据统计，每生产1 t 烧结矿产生的显热量为1.02 GJ，烧结矿余热占我国钢铁余热资源总量的8%[1-3]。环形冷却机以气固交叉错流换热的形式实现烧结热量回收，该设备存在回收热载体质量差、显热回收率不高、漏风等缺点。烧结余热竖罐式余热回收工艺是针对CDQ 干熄焦炉提出的，与环冷机余热回收模式相比，其吨矿发电量有望翻倍[4]。在“十二五”期间，中国有2 台竖罐式余热回收工程得以实施。然而，目前国内竖罐式烧结余热回收系统运行效果并不好，烧结余热竖罐作为整个工艺的关键设备，其结构形式如图1所示，其内部气固传热过程有待进一步研究。

图1 烧结余热竖罐结构示意图Fig.1 Schematic diagram of sinter waste heat vertical tank

近年来，人们对环冷机内气固传热过程进行了大量研究[5-9]，烧结余热竖罐内的烧结颗粒在重力作用下由罐体顶部向下缓慢移动，并在冷却段内与冷却气体换热，逐渐被冷却，是一种典型的气固逆流式换热床层，该类床层在蓄热、气体分离等工业过程中亦有广泛应用。FENG 等[10-14]针对烧结矿颗粒床层的特殊性，对其内部空隙率分布、气体流动及气固传热过程开展了理论研究。高建业等[15-16]采用解析的方法建立了竖罐解析计算模型，研究了单一参数对竖罐气固换热过程的影响，进而确定竖罐热工参数的取值范围。FENG等[17]通过嵌入内热源形式，建立了竖罐3维稳态模型，初步探索了年冷却390 万t 烧结矿竖罐的热工参数组合。PAN等[18]提出了一种研究竖罐内传热和流动过程的解析方法，分析了冷却风量、冷却时间、装置高度和压降之间的响应关系。ZHANG 等[19]提出将量纲一㶲耗作为竖罐余热回收效果的评判标准，分析了各影响因素对其产生的影响。FENG等[20]推导了烧结矿竖式移动床层内气固换热的平均㶲传递努塞尔数，并对不同实验工况下的㶲传递特性进行了研究。LIANG 等[21]建立了气固逆流运动床中颗粒和气体能量方程的拉格朗日方程，研究了颗粒粒径和气速对热回收过程的影响。以上研究均采用流体力学商业计算软件对烧结余热竖罐进行数值模拟，由于竖罐几何尺寸较大，导致数值计算成本较高，不利于多参数影响研究及后期工程设计应用。

本文作者推导气固逆流运动床中气固两相能量方程，通过MATLAB编写基于Runge-Kutta方法求解的计算程序，并借助小试试验验证该方法的可靠性；提出以出口冷却气体净㶲作为竖罐余热回收效果的热力学评价指标，研究烧结矿冷却温度、冷却气体进口速度及冷却段直径3个关键参数对竖罐余热回收过程的影响，以获取不同工况条件下所需竖罐冷却段高度、罐体内的温度分布以及压降的情况，最终在前期研究的基础上，对3个热工参数灵敏度进行分析。该研究可为烧结余热竖罐前期设计与后期调试提供理论参考。

1 数学模型

1.1 控制方程描述

烧结余热竖罐内气固逆流传热过程如图2所示。图2中：Ts,in和Ts,out分别为烧结矿进口、出口温度；Tg,in和Tg,out分别为冷却气体进口、出口温度；l为微元段所处高度；Δl为微元段长度。由图2可见：高温颗粒从床层顶部进入，在重力作用力下以极为缓慢的速度向下运动，另一方面，低温冷却气体由床层底部进入与颗粒逆向而行，两者间产生热量交换。本节建立移动床中颗粒和气体能量方程，数值研究床层内颗粒-气体的传热行为。该模型基于以下假设：1）颗粒具有恒定的物理性质，气相遵循理想气体定律；2）床体外壁面绝缘良好，视为绝热；3）忽略两相在水平方向温度的差异，只考虑轴向的变化。

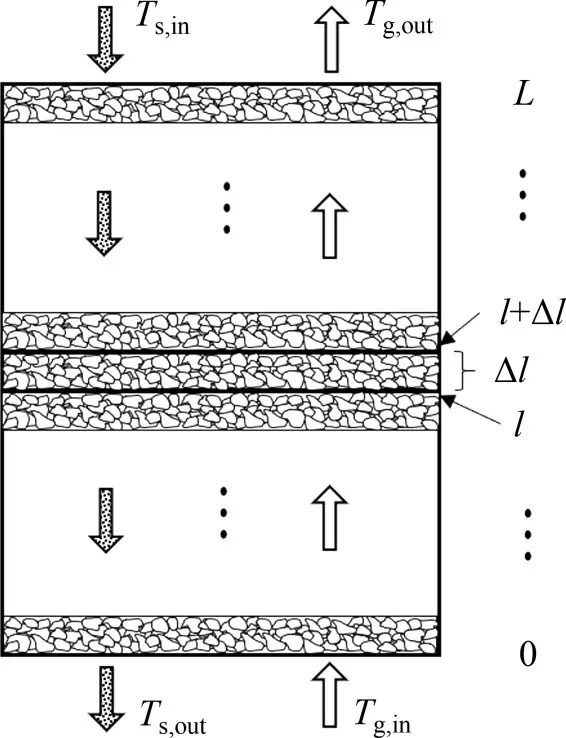
图2 气固逆流式床层示意图Fig.2 Sketch of gas-solid counter current bed

从以固相角度出发，在厚度为Δl的控制微元段内，由于颗粒以恒定的速度向下运动，其上下界面持续有固相流进、流出，根据热力学第一定律，有

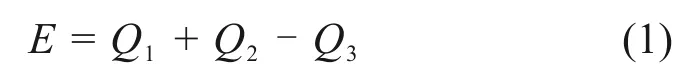
式中：E为微元体中烧结矿能量变化；Q1为进入微元体烧结矿热量；Q2为以导热形式传递进入微元体的热量；Q3为微元体内烧结矿传递给气体的热量。

在单位时间dτ内，微元体中烧结矿热力学能的变化量为：

式中：ε为空隙率；ρs为烧结矿，kg/m3；cs为烧结矿比热容，J/（kg·K）；A为床层横截面积，m2；Ts为固体温度，K；τ为时间，s；D为床层直径，m。

烧结矿颗粒在重力及底部卸料阀控制作用下，以稳定且缓慢的速度下移，单位时间由l+Δl截面位置进入微元体烧结矿的焓Q1,in为

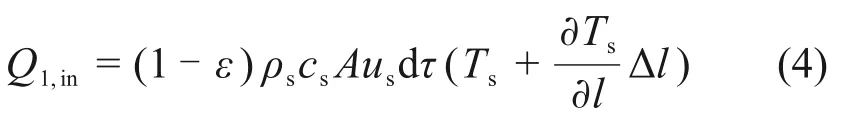
单位时间由l截面出微元体的烧结矿焓Q1,out为

式中：us为烧结颗粒下移速度。

由导热引起的在单位时间内传递给微元体的热量为

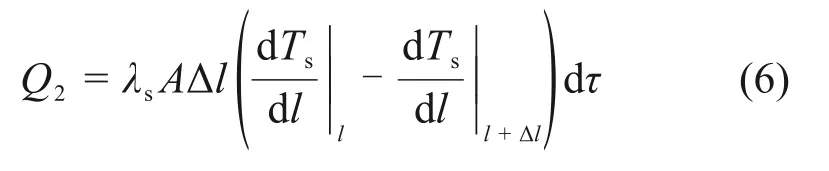
微元体内烧结矿与冷却气体之间存在温差，在其对应的微元内定义固体平均温度Ts和气体平均温度Tg。考虑到两者之间的换热过程，单位时间烧结矿传递给气体的热量为

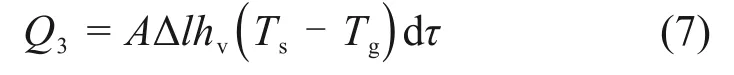
式中：hv为烧结矿与冷却气体间体积对流换热系数。

将（2）、（4）～（7）式代入式（1），通过化简整理可得微元段内烧结矿能量方程：

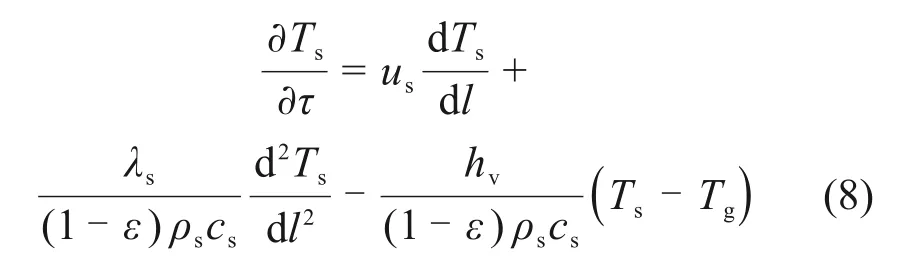
同理可得气体能量方程为

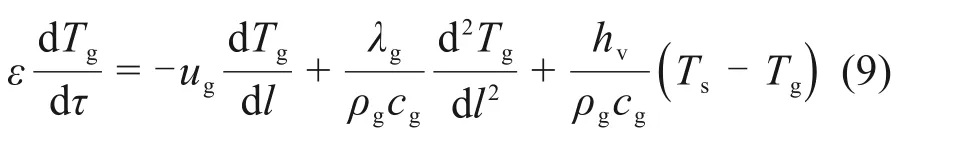
式中：Tg为气体温度，K；ug为气体表观流速，m/s；ρg为空气密度，kg/m3；cg为气体质量定压热容，J/（kg·K）；λg为气体导热系数，W/（m·K）。通过实验获取传热系数hv如下[22]：

其中，

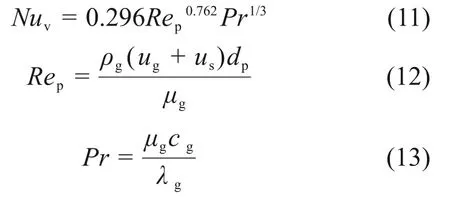
式中：Nuv为体积努塞尔数；Rep为颗粒雷诺数；Pr为气体普朗特数；dp为颗粒直径，m；μg为气体黏度，kg/（m·s）。

由于床层内冷却气体与烧结矿的逆向流动，在两相相对运动速度恒定不变时，认为床层内任意位置处于热力学稳定状态，即两相温度不随时间发生变化，因此，忽略能量守恒方程中的非稳态相项，由此可得：

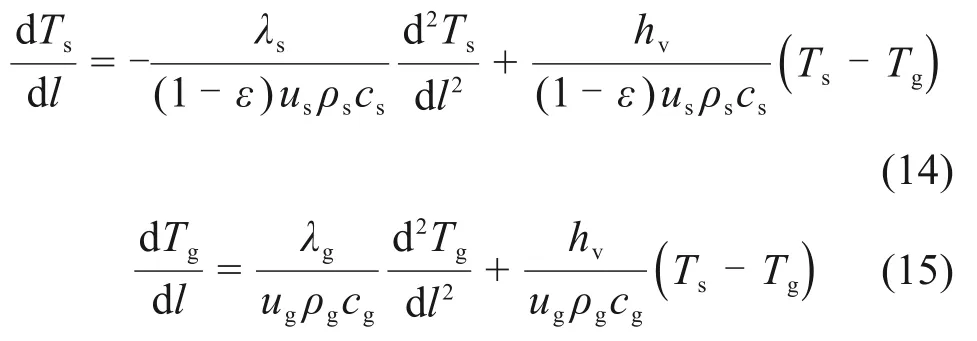
式（14）中所涉及的烧结矿及气体参数如表1所示[23-24]。

表1 烧结矿及冷却气体参数Table 1 Properties of sinter and cooling air

1.2 定解条件及求解过程

为求解式（14）和式（15），需4 个初始条件。l=0处为冷却气体进口，亦为烧结矿出口，冷却气体的进口温度是确定值，烧结矿颗粒的出口温度可以根据冷却工艺要求进行设置。在罐体底部边界处，忽略烧结矿与冷却气体的导热损失，由此可得：

在之后对竖罐结构与操作参数进行设计计算过程中，为保证颗粒与冷却气体进行充分的热量交换，需保证烧结矿进口温度的计算值与设定值一致时，迭代才能结束。根据工艺温度要求，确定每组工况条件下所需冷却段高度以及温度沿竖罐高度的分布状况。采用MATLAB编写计算程序，对式（14）和式（15）采用Runge-Kutta 方法求解，具体计算过程如图3所示。

图3 设计计算流程图Fig.3 Flow chart of design calculation

1）根据工艺温度要求及工况条件，确定烧结矿出口温度及冷却气体进口温度。

2）竖罐的结构尺寸影响烧结矿在罐体内的下移速度，进而影响冷却气体的分布及流速，从而影响罐体内气固换热过程。

3）选取某一求解范围L，即冷却段高度，对二阶微分方程进行求解，获取该冷却段高度情况下，烧结矿及冷却气体沿高度的分布曲线。

4）对比求解得烧结矿进口温度，即当l=L时，烧结矿温度是否与预设温度一致，若“否”，则进行进一步判断，并根据二分法更新求解范围L，重复过程3）；若“是”，则输出结果。

1.3 模型验证

为验证模型的准确性，搭建烧结矿冷却竖罐小试试验装置，如图4所示。小试验装置烧结矿最大处理能力为5 t/h，有效冷却横截为圆形，其面积为1 m2。主体试验罐体分为2 部分，上部为加热段，有效高度为3.78 m，下部为冷却段，有效高度为1.8 m。实验装置的具体参数及操作方法见文献[19]，[22]及[25]。

图4 小试试验装置图Fig.4 Pilot test device diagram

建立与小试试验装置冷却段一致的计算模型，其冷却段室顶部烧结矿进口温度为1 071 K，质量流量为1.8 t/h，冷却气体进口温度为293 K，进口速度为0.76 m/s。在实验过程中，使用铠装热电偶测量冷却段内各高度处气固温度，测量点设置在床层高度0.5，1.0，1.5及1.8 m处。由于床层内颗粒始终处于运动状态，难以区分颗粒与气体温度，因此，将热电偶所测温度视为气固综合温度，即颗粒温度与气体温度的均值，两者权重各占0.5。将测量数值与数值计算结果进行比较，如图5所示。由图5可知：计算得到的气固温度沿床层高度的分布结果与实验测量结果吻合较好，因此，认为所建立的模型是准确、可靠的。

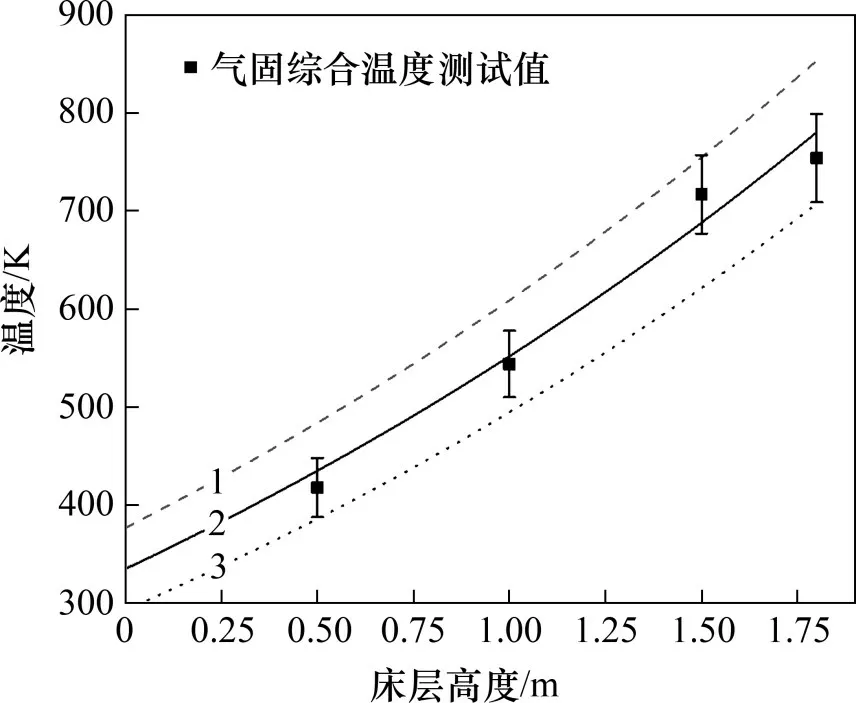
图5 实测气固温度沿床层高度变化与计算结果对比Fig.5 Comparison of measured gas-solid temperature along bed height with calculation results

2 热力学能评价指标

冷却气体在通过炽热的烧结矿床层时获得热量，然而，由于温度的差异，即使热量相同，其所具备的能量品质也存在差异。同时，冷却气体在穿过料层时，由于颗粒的阻碍产生机械㶲损失。㶲分析方法建立在热力学第一与第二定律的基础上，可以在偏离环境状态的情况下更好地分析解释工质的做功能力，揭示系统内部损失的实质，对于整个系统的热力学理论完善具有指导意义[26]。

式中：Ex为净回收㶲；ExT为温度㶲，表示冷却气体从高温烧结矿处获取的能量；ExP为压力㶲，表示由于料层内压降导致的机械能损失，两者之和即为净回收㶲[27-28]。

式中：mg为冷却气体质量流量，mg=ugAρg；Ta为环境温度，K。

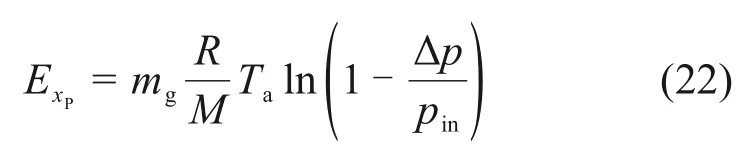
将竖罐底部出口视为大气压，则可将式（22）化为

式中：Rg为理想气体常数，取8.314 5 J/（mol·K）；pa为大气压力，Pa；Δp为料层内阻力压降，Pa。

由于pa＜pa+Δp，压力㶲计算结果小于0，对净回收㶲产生负影响，符合物理意义。采用MACDONALD 方程[29]计算料层内气流受阻所产生的压降：

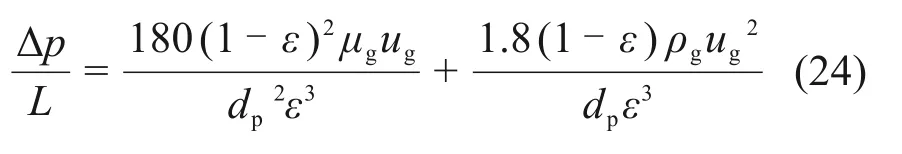
其适用范围为：dp=0.012～65.840 mm，ε=0.119～0.919，10-3＜Re＜104。

3 单因素影响分析

利用上述建立的计算方法，针对国内某年产370万t烧结机（作业率为92%，返矿率为12%），基于单罐设计，针对影响竖罐内气体流动和气固传热过程的3 个主要因素（烧结矿冷却温度、冷却气体进口速度及冷却段直径），借助控制变量法计算并分析单个因素对竖罐内气体流动和气固传热过程的影响规律，并在此基础上获取余热回收的净㶲Ex。具体热工参数及研究变量如表2所示。

表2 研究工况条件Table 2 Research operation conditions

3.1 烧结矿冷却温度

在冷却气体进口速度为4 m/s，冷却段直径为7 m 的情况下，得到不同烧结矿冷却温度条件下，烧结矿及冷却气体温度随高度变化，如图6所示。由图6可知：当竖罐底部烧结矿出口温度为373，383，393，403 和413 K 时，高温烧结矿从923 K冷却到相应温度所需冷却段高度分别为7.62，6.39，5.55，4.92 和4.41 m。随烧结矿冷却温度升高，所需冷却段高度均不断减小，且减小速度逐渐减缓。这是由于在颗粒下移速度保持不变的情况下，烧结矿冷却温度的升高将需要较少的床层内换热空间，且烧结矿冷却温度越高使气固间温差增加，两者之间的换热强度增强，因此，需要的热交换空间较少。

图6 不同烧结矿冷却温度条件下，烧结矿及冷却气体温度随高度变化曲线Fig.6 Variation curves of sinter and cooling gas temperature with bed height at different sinter cooling temperature conditions

图7所示为冷却气体出口温度及料层内总压降随烧结矿冷却温度变化规律。由图7可知：随烧结矿冷却温度升高，气体出口温度和床层内气流压降均逐渐下降。这是由于烧结矿冷却温度的升高将导致床层内固相传递给气相的热量减少，根据热量守恒定律气体出口温度降低。另外，烧结矿冷却温度升高会使所需床层高度降低，冷却气体的行程随之缩短，如式（24）所示。在其他参数不发生变化的情况下，床层内总气流压力降会逐渐降低。

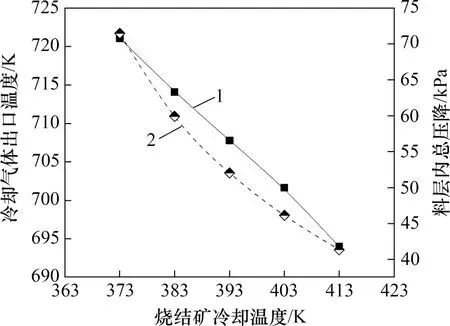
图7 冷却气体出口温度及料层内总压降随烧结矿冷却温度变化曲线Fig.7 Variation curves of sinter cooling gas outlet temperature and total pressure drop in bed with sinter cooling temperature

图8所示为竖罐出口冷却气体温度㶲、压力㶲和净㶲随烧结矿冷却温度的变化规律。由图8可知：随烧结矿冷却温度增加，出口气体的温度㶲逐渐降低，而压力㶲则逐渐升高。这是因为烧结矿冷却温度升高将导致空气出口温度降低，由式（21）可得，出口气体的温度㶲会逐渐降低。而另一方面，床层内气流压力降降低，使压力㶲升高（㶲损失减少）。温度㶲与压力㶲两者同等减和增，导致净㶲不发生变化。

图8 温度㶲、压力㶲及净㶲随烧结矿冷却温度关系曲线Fig.8 Variation curves of temperature exergy,pressure exergy and net exergy with sinter cooling temperature

3.2 冷却气体进口流速

在烧结矿冷却温度为393 K，冷却段直径为7 m，冷却气体进口速度不同条件下，烧结矿及冷却气体温度随高度变化如图9所示。由图9可知：当冷却气体进口速度为3.2，3.6，4.0，4.4 和4.8 m/s时，所需冷却段高度分别为9.10，6.82，5.55，4.72 和4.14 m，随速度增加，冷却段高度逐渐减小。这是由于气体的进口速度增加，会导致罐体内气体与烧结矿颗粒之间的碰撞加剧，气固之间的换热强度增强，因此，将烧结矿冷却至目标温度需要的冷却空间更小。

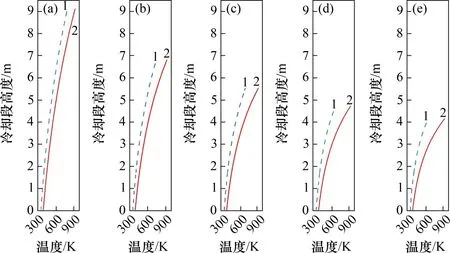
图9 不同冷却气体进口流速条件下，烧结矿及冷却气体温度随高度变化曲线Fig.9 Variation curves of sinter and cooling gas temperature with bed height at different cooling gas inlet speed conditions

图10所示为冷却气体出口温度及料层内总压降随冷却气体进口速度变化规律。由图10可知：随冷却气体进口速度增加，出口气体温度逐渐降低，速度每增加0.4 m/s，出口气体温度降低39 K。这是由于冷却气体进口速度会导致罐体内冷却气体流量增加，烧结矿进出口热容量差不变，根据热力学第一定律可知，冷却气体进口流量增加必然会导致气体出口温度减小。随冷却气体进口速度增加，料层内总压降呈现出先降低后增加的趋势，根据式（24）可知，气体速度增加会导致单位高度料层内压力降增加，亦会导致所需冷却段高度降低。当冷却气体进口速度小于3.7 m/s时，随速度增加，冷却段高度降低对内料层内压降的削减作用比单位料层内压力降升高产生的削减作用大，因此，料层内压力降逐渐降低；当冷却气体进口速度大于3.7 m/s 时，单位料层内压力降升高占主导影响，此时，料层内压力降随冷却气体进口速度增加而升高。

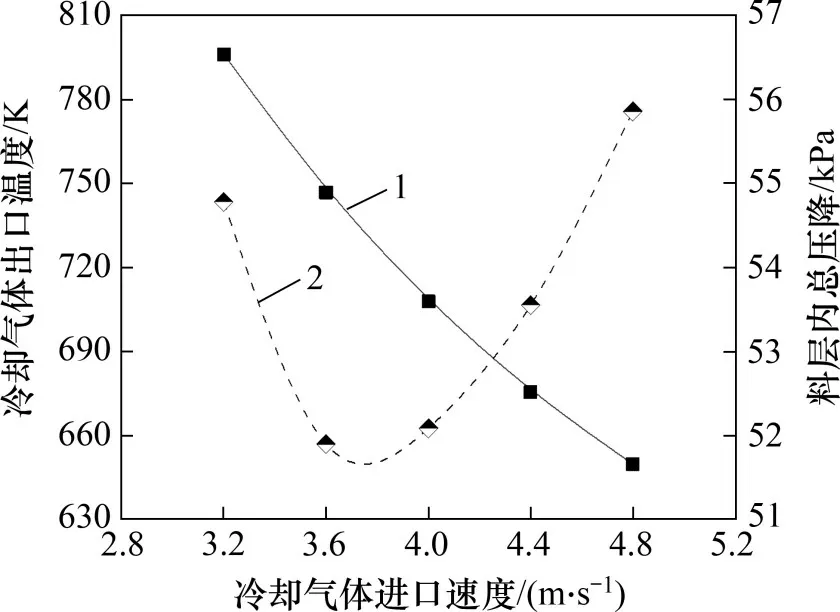
图10 冷却气体出口温度及料层内总压降随冷却气体进口速度变化曲线Fig.10 Variation curves of sinter cooling gas outlet temperature and total pressure drop in bed with cooling gas inlet speed

图11所示为竖罐出口冷却气体温度㶲、压力㶲和净㶲随冷却气体进口速度的变化规律。由图11可知：随冷却气体进口速度增加，出口气体的温度㶲、压力㶲和净㶲均逐渐降低。这是因为在烧结矿进口热容量不变的情况下，冷却气体从烧结矿获取的热量亦恒定，然而，出口气体温度随冷却气体进口速度增加而不断降低，回收余热的品质不断降低。此外，气体进口速度增加会导致罐体内气体受烧结矿颗粒阻碍的影响更加明显，机械能损失增加，使压力㶲降低。冷却气体进口速度每增加0.4 m/s，会导致净㶲减小1.4 MJ/s。

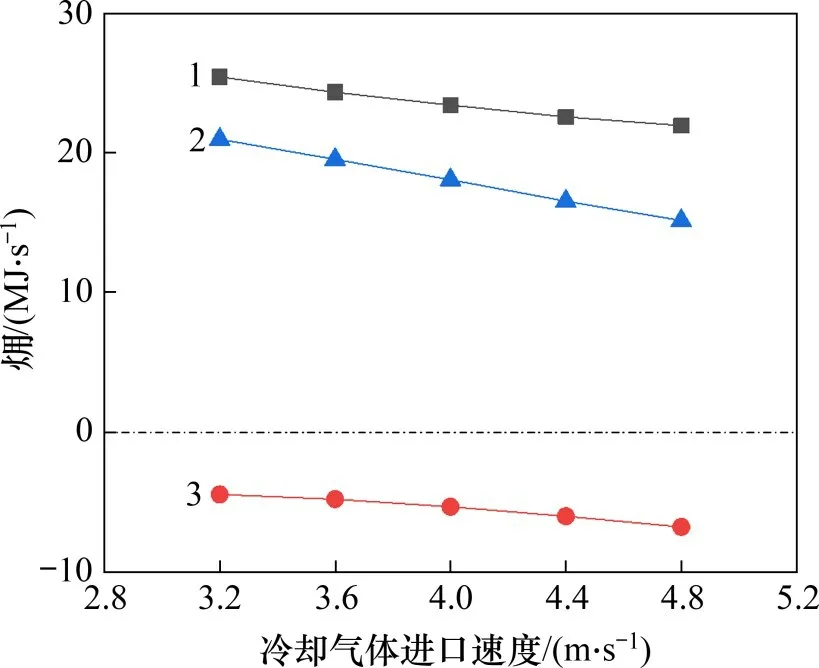
图11 温度㶲、压力㶲及净㶲随冷却气体进口流速关系曲线Fig.11 Variation curves of temperature exergy,pressure exergy and net exergy with cooling gas inlet speed

3.3 冷却段直径

在烧结矿冷却温度为393 K，冷却气体进口速度为4 m/s，冷却段直径不同条件下，烧结矿及冷却气体温度随高度变化如图12所示。由图12可知：当冷却段直径为6.0，6.5，7.0，7.5 和8.0 m时，所需冷却段高度分别为12.95，7.78，5.55，4.28和3.45 m。随冷却段直径增加，所需冷却段高度均不断减小。这是由于在冷却气体进口速度保持不变的情况下，冷却段直径增加会导致冷却气体流量增加，烧结矿的冷却速度加快。

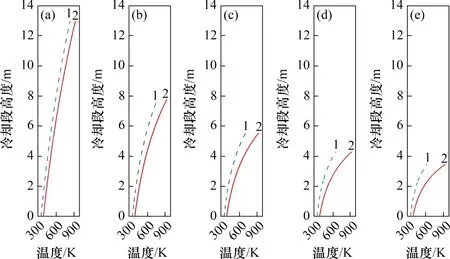
图12 不同冷却段直径条件下，烧结矿及冷却气体温度随高度变化曲线Fig.12 Variation curves of sinter and cooling gas temperature with bed height at different cooling section diameter conditions

图13所示为冷却气体出口温度及料层内总压降随冷却段直径变化规律。

图13 冷却气体出口温度及料层内总压降随冷却段直径变化曲线Fig.13 Variation curves of sinter cooling gas outlet temperature and total pressure drop in bed with cooling section diameter

从图13可以看出：随冷却段直径的增加，出口气体温度逐渐降低，直径每增加0.5 m，出口气体温度降低53 K。这是由于在冷却段底部气体进口流速恒定的条件下，冷却段直径增加会导致罐体横截面积增加，进而导致冷却气体流量增加。单位质量冷却气体所匹配的烧结矿质量减少，根据热力学第一定律可知气体出口温度降低。随冷却段直径增加，料层内总压降逐渐降低，且趋势逐渐减缓。根据式（24）可知单位料层阻力不发生变化，随冷却段直径增加，所需冷却段高度降低，进而导致料层内总压力降低。

图14所示为竖罐出口冷却气体温度㶲、压力㶲和净㶲随冷却段直径的变化规律。由图14可知：随冷却段直径增加，出口气体的温度㶲逐渐降低，而压力㶲则逐渐升高。这是因为冷却段直径增加将导致冷却气体流量增加，进而导致气体出口温度降低，热量品质下降，表现为温度㶲降低。而另一方面，床层内气流压力降降低，使压力㶲升高。净㶲呈现出下降趋势，下降速度略有增加。

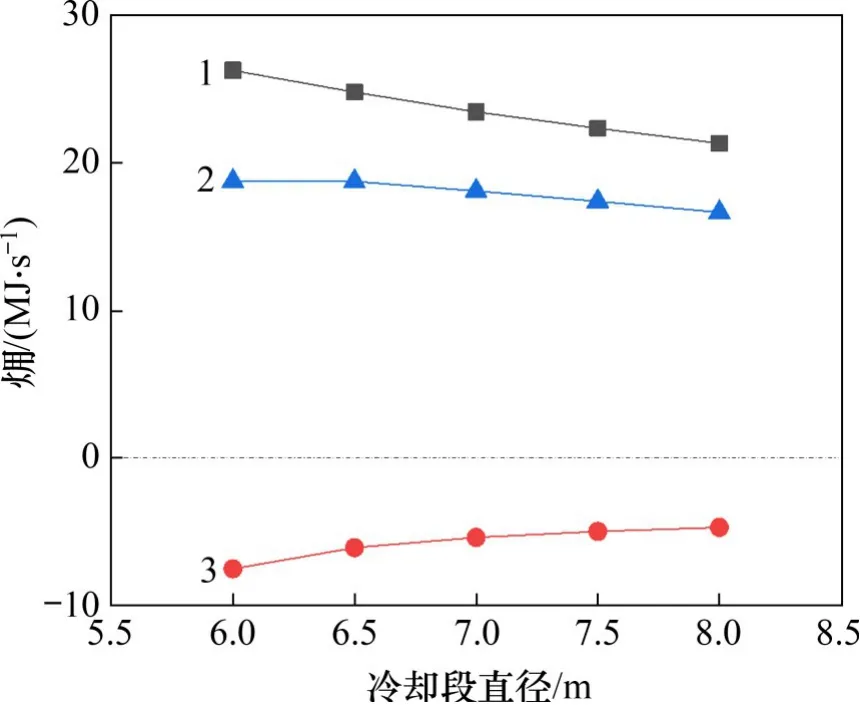
图14 温度㶲、压力㶲及净㶲随冷却段直径关系曲线Fig.14 Variation curves of temperature exergy,pressure exergy and net exergy with cooling section diameter

4 热工参数敏感度分析

余热竖罐的热工参数与整个余热回收过程有着密切联系，由于参数的组合形式众多，因此，了解热工参数与冷却段高度及净㶲的影响关系及程度，可以在进行前期设计及后期调试过程中，优先确定和调整关键参数。

4.1 样本扩充

为了扩大计算数据的样本容量，采用拉丁超立方方法进行样本抽样[30]，该方法引入“分层”的概念，在采样过程中确保样本空间分布随机的同时不发生团聚现象，即确保样本在整个采样空间内有较高的覆盖率，抽样结果如表3所示。

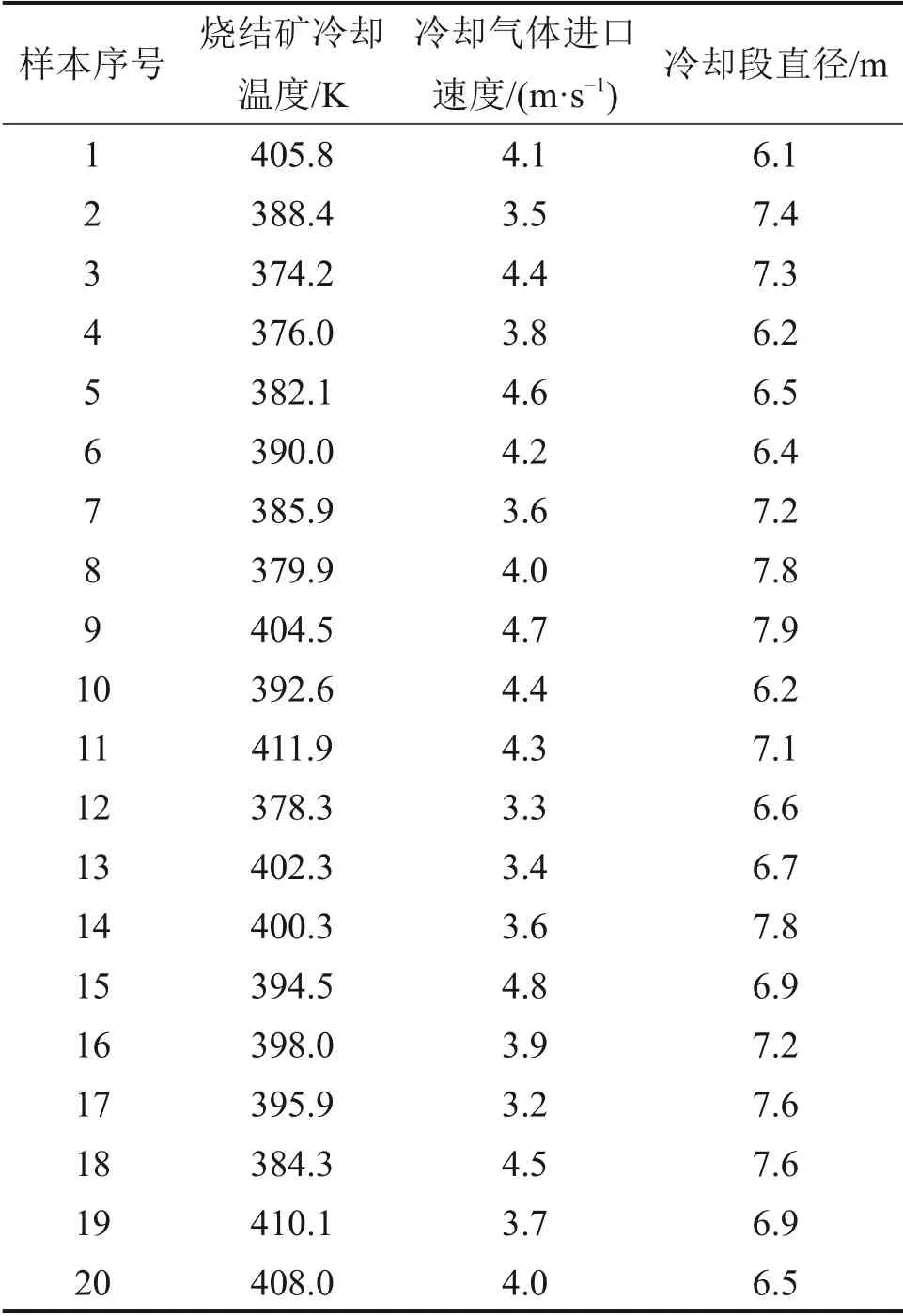
表3 拉丁超立方抽样结果Table 3 Results of latin hypercube sampling

将抽样结果代入所建立的数学模型中，计算结果如图15所示。

图15 各样本对应计算结果Fig.15 Corresponding calculation results of each sample

4.2 敏感度分析

将灵敏度分析应用于烧结余热竖罐的设计中，可以明确结构与操作参数对目标参数的影响程度。对模型灵敏度采用Sobol法进行分析，判断其全局敏感性，Sobol 法基于模型分解思想，能够有效求解高度非线性模型中参数相互作用产生的灵敏度，通过将模型数据代入灵敏度方法，得到显著性影响因子对输出结果的影响占比[31]。对影响竖罐余热回收过程的3个参数进行全局灵敏度分析，得到冷却段高度及净㶲的灵敏度指标，如图16所示。

图16 烧结余热竖罐响应参数灵敏度Fig.16 Response parameter sensitivity of sintering waste heat vertical tank

由图16可知：在研究范围内，冷却段直径对冷却段高度的影响程度最大，而烧结矿冷却温度与冷却气体进口速度对其的影响程度较低，两者基本一致；另一方面，冷却气体进口速度及冷却段直径对净㶲均有明显影响，冷却气体进口速度的影响最大，后者的影响次之，而烧结矿冷却温度对净㶲的影响依旧很小，灵敏度低于20%。因此，在研究范围内，烧结矿冷却温度对竖罐余热回收过程不敏感。

5 结论

1）建立了基于移动床的逆流式换热床中颗粒和气体能量方程，以烧结矿及冷却气体进出口温度作为初始条件和收敛条件，通过更新冷却段高度，求解微分方程从而获取床层内气固温度沿高度变化曲线。采用小试试验验证了模型的可靠性，有效降低了设计计算成本。

2）随烧结矿冷却温度、冷却气体进口速度及冷却段直径增加，竖罐所需冷却段高度均逐渐降低：随烧结矿冷却温度从372 K 升高至413 K，所需冷却段高度从7.62 m降低至4.41 m；随冷却气体进口速度由3.2 m/s 增加至4.8 m/s，所需冷却段高度逐渐由9.10 m 降低至4.14 m；随冷却段直径从6.0 m 增加至8.0 m，所需冷却段高度从12.95 m 降至3.45 m。

3）综合考虑热量回收的品质与机械能耗，以净㶲作为余热回收效果评判指标，发现烧结矿冷却温度变化对净㶲影响不大；随冷却气体进口速度增加，出口气体的净㶲呈线性降低；随冷却段直径增加，出口气体净㶲逐渐降低，且下降速度逐渐加速。

4）在研究范围内，冷却段直径对冷却段高度的影响程度最大，而烧结矿冷却温度与冷却气体进口速度对其的影响程度较小。冷却气体进口速度及冷却段直径对净㶲均有明显影响，前者的影响最大，后者的影响次之，烧结矿冷却温度对净㶲的影响最小。