不同流型浆液在裂隙内扩散规律的理论与数值分析

王东亮，郝兵元，梁晓敏

（太原理工大学矿业工程学院，山西太原，030024）

注浆是巷道围岩加固和地下工程堵水的常用技术手段[1]。随注浆技术的发展，浆液材料的来源也越来越广泛，其中水泥材料应用极为普遍[2]。在进行裂隙注浆时，浆液在裂隙内的扩散规律（特别是压力场的变化情况）是注浆效果的重要影响因素。

目前，在水泥浆液的流型与扩散规律方面，阮文军等[3-4]通过实验研究分析了浆液的流变性和可注性，并通过理论分析与计算机编程建立了宾汉姆流体在裂隙内的扩散模型。在研究裂隙注浆时，刘人太等[5-6]探究了C-S 浆液和GT-1 浆液在裂隙中流动的浆液扩散形态及注浆压力场变化规律，但并未说明这2 种浆液的流型；魏久传等[7]根据步进式算法，分别探究了C-S浆液在恒速下及硅溶胶浆液在恒压下的扩散规律，但2种浆液的控制条件不同，难以进行对比。周子龙等[8]将浆液视为幂律流体，推导出了浆液压降及浆液扩散的表达式；BAKER等[9-11]将浆液视为牛顿流体，建立了裂隙注浆的浆液扩散模型；刘滨等[12-13]将浆液视为牛顿流体，分析了浆液黏度、裂隙开度等对浆液扩散距离及浆液压力场的影响；李术才等[14]将浆液视为宾汉流体，建立了基于浆-岩耦合效应的浆液扩散方程；杨志全等[15-16]根据宾汉姆流体的本构方程，推导出了球及柱型浆液扩散方程，并通过物理实验对方程进行了验证。

以上研究均将浆液看作固定流型的流体，实际中注浆浆液由于水灰比等参数的不同，会有不同的流型。在推导浆液扩散方程时，以往研究多是根据N-S 方程，将注浆口压力看作常数进行推导，实际上，N-S方程中包含速度和压力，而注浆时可采用恒速注浆或恒压注浆，当采用恒速注浆时，注浆口压力时刻变化，因此，将浆液压力作为研究对象时，其表达式中存在注浆口压力这个变量，且研究中在验证扩散方程时，实验条件难以与理论条件保持完全一致，这使理论方程的验证存在较大困难。

为解决以上问题，本文作者将水泥浆液视为牛顿流体、宾汉姆流体和幂律流体3种流型，根据不同流体的本构方程及运动方程，基于一些假设，推导出3种流体的扩散方程，用浆液压力损失作为分析浆液扩散情况的标准，避免因表达式中存在注浆口压力等变量造成的浆液压力求解的不便，并通过数值模拟对浆液扩散方程进行对比验证，分析裂隙注浆过程中浆液压力场的变化规律。

1 理论模型

1.1 基本假设

1）浆液视为各向同性且不可压缩的均质流体，且不考虑注浆过程中浆液流型的变化。

2）浆液在裂隙中的流动为层流，且符合连续方程。

3）不考虑重力及静水压力的影响。

4）裂隙为单一水平裂隙，且符合无滑移边界条件。

5）不考虑流固耦合作用，即忽略注浆过程中裂隙的变形。

1.2 浆液扩散计算模型

根据基本假设4），假定裂隙为单一水平裂隙，即裂隙面是平行的且与水平方向夹角为0°。根据基本假设1），浆液是各向同性的，因此，为方便计算，可对浆液沿水平方向x轴的流动进行研究[17]，计算模型如图1所示。

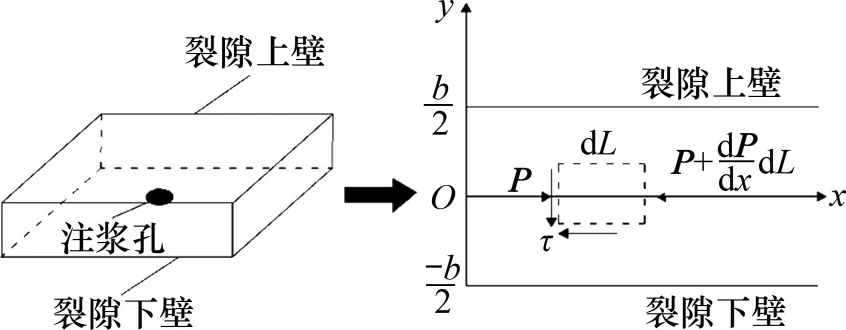
图1 浆液扩散计算模型Fig.1 Calculation model of grout diffusion

1.3 浆液流型

1.3.1 流型分类

在研究浆液的流型时，大多数学者根据流体的流变曲线与本构方程对浆液流型进行分类[18-19]。孙小康[20]认为，普硅425 水泥浆在其水灰比W/C≥0.7 时为宾汉姆流体，当水灰比W/C≤0.6 时为幂律流体。刘人太[21]认为，水泥浆液在其水灰比较大时可视为牛顿流体，黏土水泥浆液与较大黏度的化学浆液可视为宾汉姆流体。张凯文[22]根据注浆浆液的流变曲线对浆液进行流型分类，如图2所示。

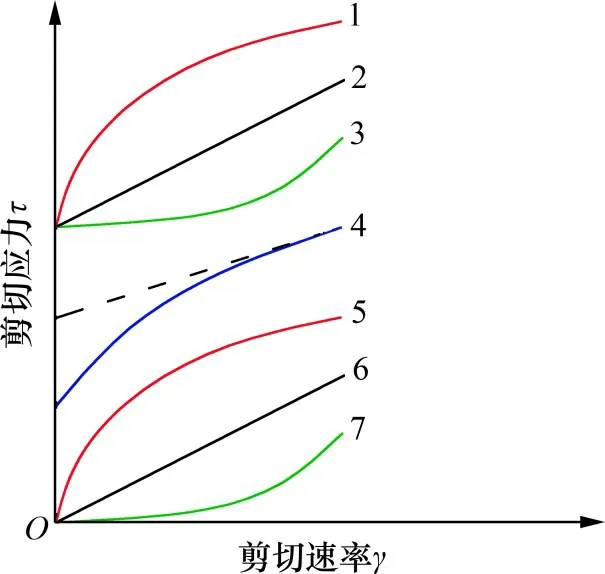
图2 浆液流体的流变曲线Fig.2 Curves of grout fluid rheological

阮文军[4]对各种常用的注浆浆液进行研究，并对浆液流型进行了分类，根据水灰比的不同，水泥浆液可分成3类流型：幂律流体（0.5≤W/C≤0.7）、宾汉姆流体（0.8≤W/C≤1.0）和牛顿流体（W/C≥2）。

本文主要研究水泥浆液在裂隙中的扩散，因此根据阮文军[4]的研究，着重分析牛顿流体、宾汉姆流体和幂律流体这3种流体的扩散规律。

1.3.2 本构方程

牛顿流体的本构方程为

式中：τ为流体剪切应力；μ为流体黏度；γ为剪切速率。

宾汉姆流体的本构方程为

式中：τ0为屈服应力。

幂律流体的本构方程为

式中：K为稠度系数；n为流变系数。

2 裂隙注浆浆液扩散方程

2.1 牛顿流体扩散方程

参照单裂隙立方定律[23-25]的推导方法，现推导牛顿流体的扩散方程。

忽略浆液的压缩性，浆液在单一裂隙内的流动满足N-S方程[26]：

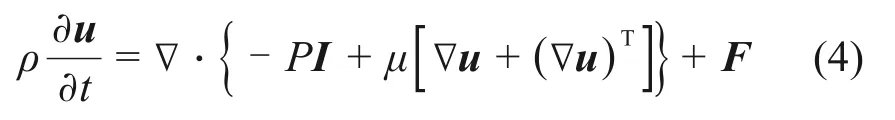
式中：ρ为浆液流体的密度；u为流体流速矢量；t为流动时间；∇为散度算子；P为浆液压力；I为流体单位张量；F为单位体积流体所受的外力。

当牛顿流体进行稳定层流时[20]，式（4）可改写为：

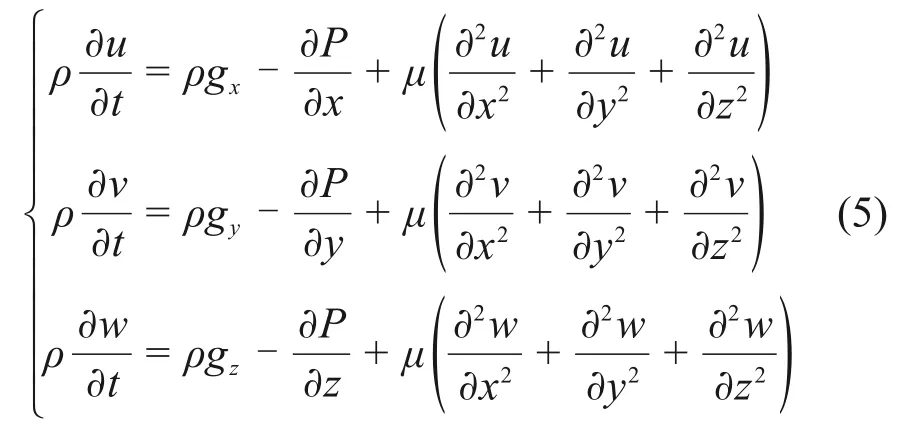
式中：u，v和w分别为流体流速沿x，y和z方向的分量；gx，gy和gz分别为体积力沿x，y和z方向的分量。

由于流体在裂隙中的流动为稳定层流，且本文取x轴方向为流体流动方向，因此流体仅有x轴方向的速度分量，即v=w=0。由基本假设2）可知，流体流动满足连续方程：

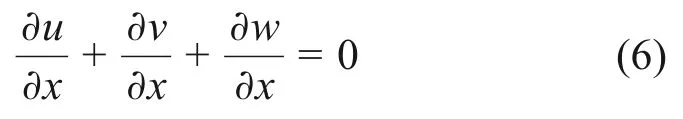
对式（7）进行重积分得

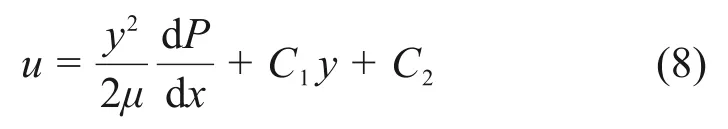
式中：C1和C2为常数。

由基本假设4）可知，裂隙边界为无滑移边界，即在裂隙表面处流体流速为0，因此，当y=-b/2时，u=0；当y=b/2时，u=0，代入式（8）得

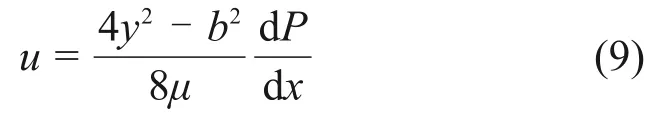
则在裂隙内流体流动的单位流量为

式中：q为流体的单位流量；x为流体在t时刻的扩散半径。

式（12）即为单裂隙立方定律[23-25]的变形形式。

整理式（12）得

将式（13）进行积分得

式中：C3为常数。

由于在x=rc处，P=Pc，将此初始条件代入式（14）可得

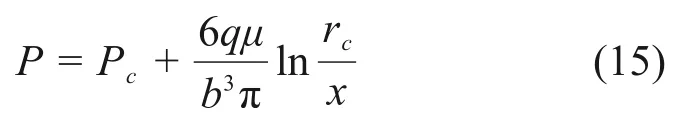
式中：Pc为注浆孔口处的注浆压力；rc为注浆孔半径。

由于浆液压力在流动过程中会有损失，根据式（15）可以得到浆液压力损失的表达式：

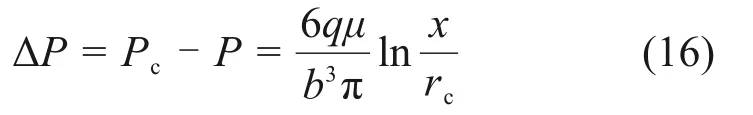
式中：ΔP为浆液在流动过程中的浆液压力损失。

式（16）即为牛顿流体的浆液扩散方程。

2.2 宾汉姆流体扩散方程

参照上述牛顿流体扩散方程的推导方法，结合宾汉姆流体的本构方程，现推导宾汉姆流体的扩散方程。

根据张凯文[22]的研究，浆液在裂隙内的扩散满足质量守恒定律，由图1可得

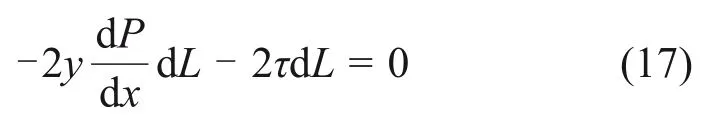
式中：dL为流体微元段沿x方向的长度；为流体微元沿x方向的压力变化量。

根据式（17）可知，剪切应力τ应满足：

宾汉姆流体在裂隙内流动时，其内部存在一个剪切应力为0的区域，在这个区域中，流体颗粒间无相对位移，此区域成为宾汉姆流体的流核[27]。假设流核高度为h0，则流体剪切应力τ的分布为

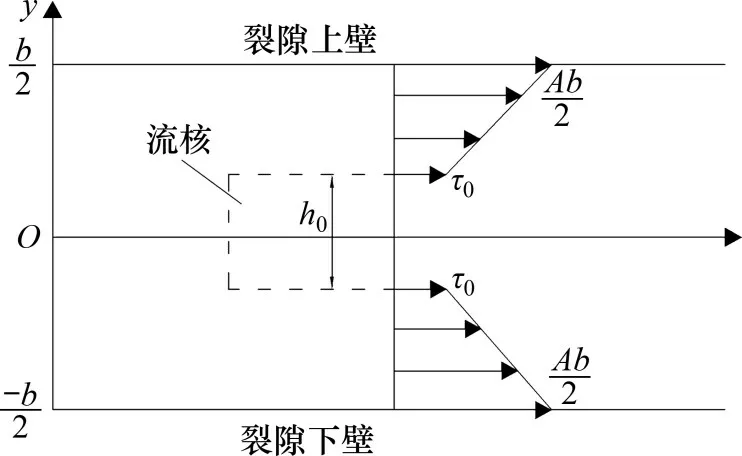
图3 宾汉姆流体剪切应力分布图Fig.3 Shear stress distribution of Bingham fluid

在流核外，有

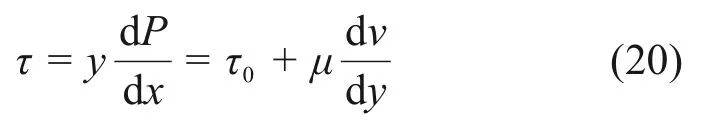
整理式（20）得

对式（21）进行积分得

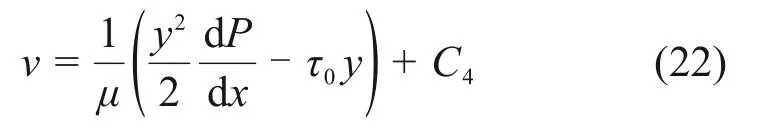
式中：C4为常数。

由式（4）可知，裂隙边界为无滑移边界，将边界条件y=b/2，v=0代入式（22），得流核外的速度v1表达式为

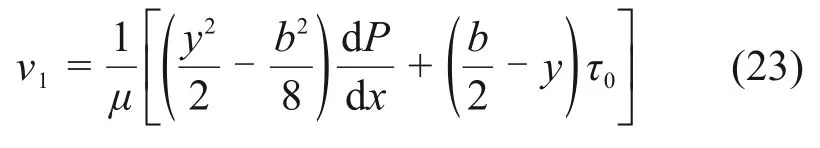
在流核内，流体速度为定值，与y无关，则裂隙内流体的流速分布为

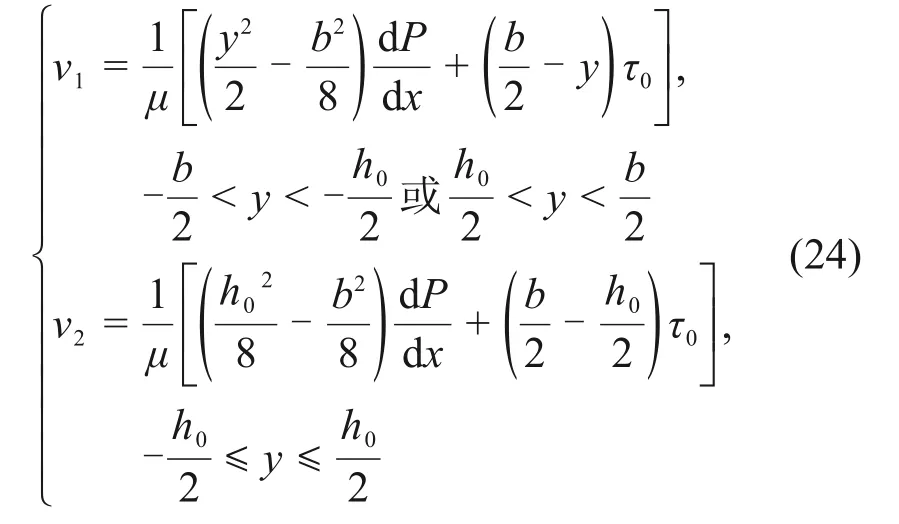
由于速度的对称性，流体在裂隙内的流速沿中心线上下对称，则裂隙内流体的平均流速为：

将τ0=代入式（26）得

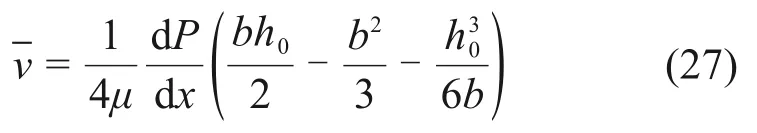
由于宾汉姆流体的流核区域很小[27]，即h0远小于b，所以式（27）中h30/6b趋近于0，因此式（27）可简化为

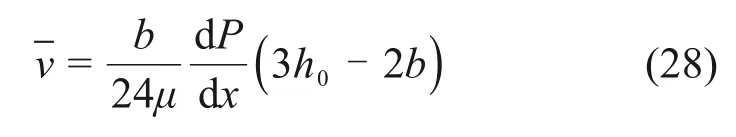
则在裂隙内流体流动的单位流量为

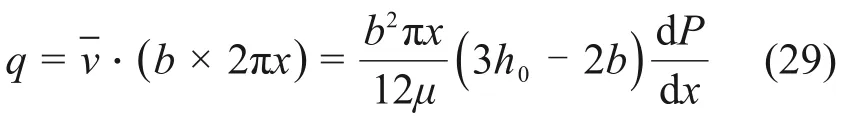
将τ0=代入式（29）得

对式（30）积分得

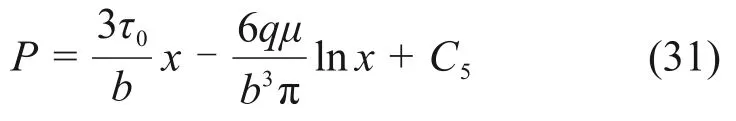
式中：C5为常数。

由于在x=rc处，P=Pc，将此初始条件代入式（31）可得浆液压力的表达式：

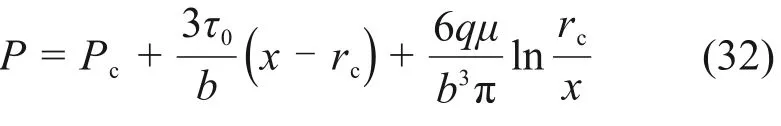
则浆液压力损失的表达式为

由于图1中剪切应力方向与图3中相反，屈服剪切应力为负值，因此，式（33）可改写为

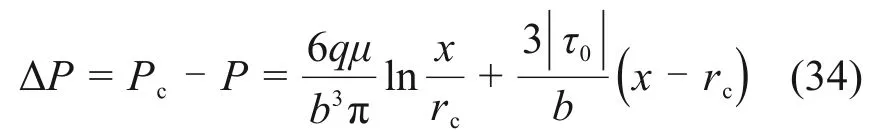
式（34）即为宾汉姆流体的浆液扩散方程。

2.3 幂律流体扩散方程

根据王东亮等[28]的研究，当裂隙开度为b时，幂律流体在裂隙内扩散时的浆液压力表达式为

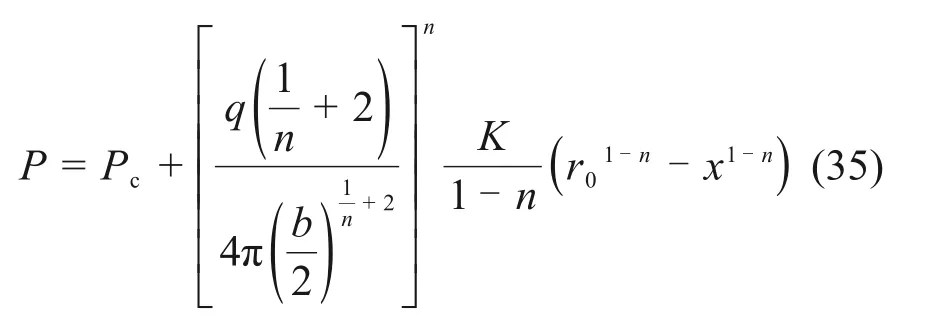
则浆液压力损失的表达式为

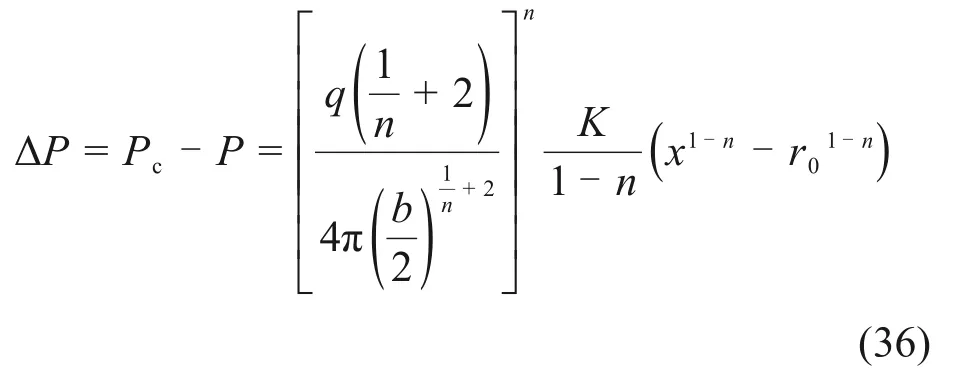
式（36）即为幂律流体的浆液扩散方程。

3 裂隙注浆数值模拟

3.1 牛顿流体扩散数值模拟

3.1.1 模型建立

由式（16）可知，牛顿流体浆液压力损失与流量q、黏度μ呈正比，与裂隙开度b的立方呈反比，基于单一变量原则，建立如表1所示的工况对浆液扩散规律进行数值模拟研究。

表1 牛顿流体工况设计表Table 1 Working condition design table of Newtonian fluid

利用数值模拟软件COMSOL Multiphysics的层流模块，建立单一水平裂隙模型。模型长×宽×高为20 m×20 m×20 m，裂隙宽度依照工况进行设计，注浆孔的半径为2.5 cm，浆液密度设定为1 600 kg/m3。在层流入口设置浆液流量，在层流物理场流体属性中设置黏度，根据工况设计其他参数。根据基本假设4），裂隙表面的边界条件为无滑移。其他边界条件如下：模型上下边界为固定约束，注浆孔口为定流速。

3.1.2 裂隙开度对浆液扩散的影响

选取工况1～3进行研究，模型参数根据工况设计，分析浆液压力与裂隙开度的关系。图4所示为浆液压力在不同时间、不同裂隙开度下的分布情况，将理论计算值与模拟结果进行对比，可得注浆2 min 时浆液压力损失与扩散半径的关系如图5所示。由图4和图5可知：

图4 不同时间不同裂隙开度下浆液压力分布Fig.4 Slurry pressure distributions with different crack openings at different time

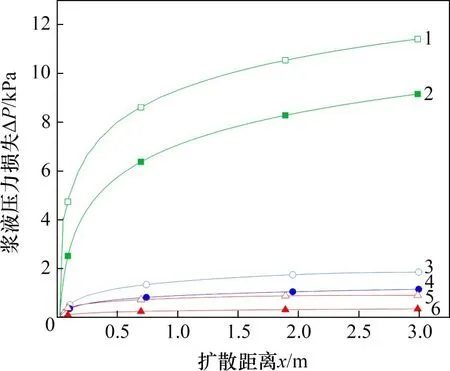
图5 不同裂隙开度下浆液压力损失与扩散半径关系Fig.5 Relationship between slurry pressure loss and diffusion radius at different crack openings

1）在相同时刻，浆液压力在注浆孔口处最大，随扩散半径增大而逐渐减小；压力等值线在注浆孔附近最密集，随扩散半径增大而逐渐变得稀疏，说明浆液压力在孔口处衰减最严重，其原因可能是浆液从注浆孔流入到裂隙中，可流动空间突然增大，导致浆液压力瞬间释放。

2）在同一位置处，浆液压力随时间延长而增大，且浆液压力是关于注浆孔对称分布的。

3）在相同时刻，当裂隙开度增加时，浆液扩散半径减小；在浆液扩散范围内的相同位置处，当裂隙开度增加时，浆液压力减小。

4）浆液压力损失与扩散半径呈正相关，随扩散距离增加而增大，且在同一位置处，压力损失与裂隙开度负相关，随裂隙开度增大而减小，这与式（16）表达的变化关系一致。

5）模拟中浆液压力损失随扩散距离的变化趋势与计算结果基本一致。在同一位置处，压力损失计算值比模拟值略小，且在注浆孔口处两者差值较小，随扩散距离增大而逐渐增大，但差值都在可接受范围内，可能是因为理论计算中未考虑裂隙表面的摩擦性，即未考虑裂隙壁对浆液流动的阻力造成的压力损失；且计算中未考虑浆液流动的惯性，即认为浆液完全是在浆液压力的驱动下流动。

3.1.3 浆液流速对浆液扩散的影响

选取工况4，2 和5 进行研究，分析浆液压力与浆液流速的关系。图6所示为浆液压力在不同时间不同浆液流速下的分布情况，2 min时浆液压力损失与扩散半径的关系如图7所示。由图6和图7可知：

图6 不同时间不同浆液流速下浆液压力分布Fig.6 Slurry pressure distributions with different slurry flow rates at different time

1）在相同时刻，浆液压力在注浆孔口处最大，随扩散半径增大而逐渐减小；压力等值线在注浆孔附近最密集，随扩散半径增大而逐渐变得稀疏，说明浆液压力在孔口处衰减最严重，其原因可能是浆液从注浆孔流入到裂隙中，可流动空间突然增大，导致浆液压力瞬间释放。

2）在同一位置处，浆液压力随时间延长而增大，且浆液压力是关于注浆孔对称分布的。

3）在相同时刻，当浆液流速增加时，浆液扩散半径增大；在浆液扩散范围内的相同位置处，当浆液流速增加时，浆液压力增大。

4）浆液压力损失随扩散距离增加而增大，且在同一位置处，压力损失与浆液流速呈正相关，随浆液流速增大而增大，这与式（16）表达的变化关系一致。

5）模拟中浆液压力损失随扩散距离的变化趋势与计算结果基本一致。在同一位置处，压力损失计算值比模拟值略小，且在注浆孔口处两者差值较小，随扩散距离增大而逐渐增大，但差值都在可接受范围内，可能是因为理论计算中未考虑裂隙表面的摩擦性，即未考虑裂隙壁对浆液流动的阻力造成的压力损失；且计算中未考虑浆液流动的惯性，即认为浆液完全是在浆液压力的驱动下流动。

3.1.4 浆液黏度对浆液扩散的影响

根据不同时间、不同注浆参数下浆液压力分布图，都可以得到相同的结论。选取工况6，2和7进行研究，浆液压力损失与扩散半径的关系如图8所示。由图8可知：

1）浆液压力损失随扩散距离增加而增大，且在同一位置处，压力损失与浆液黏度呈正相关，随浆液黏度增大而增大，这与式（16）表达的变化关系一致。

2）对比图7和图8，发现2 个图中曲线基本一致。根据式（16）可知，压力损失与浆液流速q和浆液黏度μ的乘积呈正比。工况2作为基本工况，工况4和工况5只改变了浆液流速，而工况6和工况7只改变了浆液黏度，但工况4 中q与工况2 中μ的乘积和工况6 中μ与工况2 中q的乘积相等，即q4μ2=μ6q2，同理，q5μ2=μ7q2，因此，图7和图8中曲线应基本一致，这与式（16）的表达式吻合。

图7 不同浆液流速下浆液压力损失与扩散半径关系Fig.7 Relationships between slurry pressure loss and diffusion radius with different slurry velocities

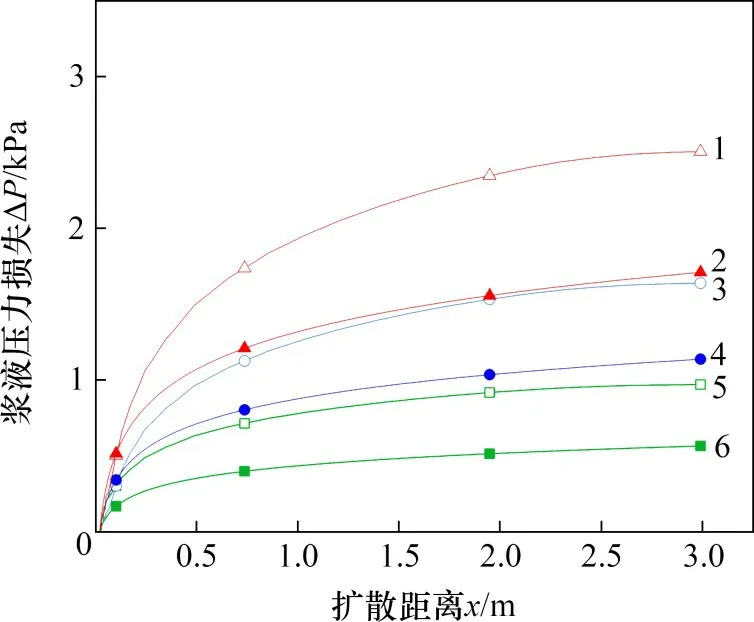
图8 不同浆液黏度下浆液压力损失与扩散半径关系Fig.8 Relationships between slurry pressure loss and diffusion radius with different slurry viscosities

3）模拟中浆液压力损失随扩散距离的变化趋势与计算结果基本一致。在同一位置处，压力损失计算值比模拟值略小，且在注浆孔口处两者差值较小，随扩散距离增大而逐渐增大，但差值都在可接受范围内，可能是因为理论计算中未考虑裂隙表面的摩擦性，即未考虑裂隙壁对浆液流动的阻力造成的压力损失；且计算中未考虑浆液流动的惯性，即认为浆液完全是在浆液压力的驱动下流动。

3.2 宾汉姆流体扩散数值模拟

3.2.1 工况设计

由式（16）和式（34）可知，宾汉姆流体的浆液压力损失比牛顿流体多了一项关于屈服应力τ0的函数，因上述研究已分析过其他参数对浆液扩散的影响，因此这里只分析屈服应力对浆液扩散的影响。屈服应力在层流物理场流体属性中设置，取值如下表2所示，其余参数的取值根据上述工况2设置。

表2 宾汉姆流体工况设计表Table 2 Working condition design table of Bingham fluid

3.2.2 结果分析

浆液压力损失与扩散半径的关系如图9所示。由图9可知：

图9 不同屈服应力下浆液压力损失与扩散半径关系Fig.9 Relationships between slurry pressure loss and diffusion radius with different yield stresses

1）浆液压力损失随扩散距离增加而增大，且在同一位置处，压力损失与屈服应力呈正相关，随屈服应力增大而增大，这与式（34）表达的变化关系是一致的。

2）模拟中浆液压力损失随扩散距离的变化趋势与计算结果基本一致。在同一位置处，压力损失计算值比模拟值略小，且在注浆孔口处两者差值较小，随扩散距离增大而逐渐增大，但差值都在可接受范围内，可能是因为理论计算中未考虑裂隙表面的摩擦性，即未考虑裂隙壁对浆液流动的阻力造成的压力损失；且计算中未考虑浆液流动的惯性，即认为浆液完全是在浆液压力的驱动下流动。

3.3 幂律流体扩散数值模拟

3.3.1 工况设计

根据式（36），浆液压力损失与流量q、稠度系数K呈正相关，与裂隙开度b呈负相关，因压力损失为指数幂形式，流变系数n为指数，因此可判断n对压力损失的影响最大。为方便研究，取流变系数为自变量研究其对浆液扩散的影响。流变系数在层流物理场流体属性中设置，取值如表3所示，取K=0.015 kg/（m·s），其余参数根据工况2设置。

表3 幂律流体工况设计表Table 3 Working condition design table of Power law fluid

3.3.2 结果分析

时浆液压力损失与扩散半径的关系如图10所示。由图10可知：

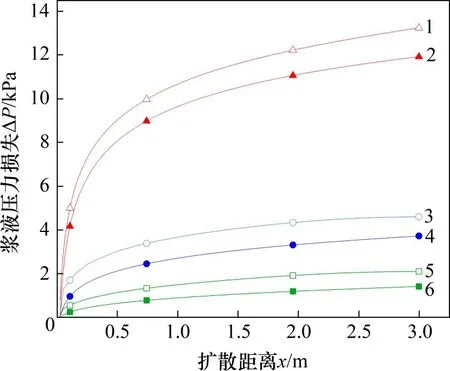
图10 不同流变系数下浆液压力损失与扩散半径关系Fig.10 Relationships between slurry pressure loss and diffusion radius under different rheological coefficients

1）浆液压力损失随扩散距离增加而增大，且在同一位置处，压力损失与浆液流变系数呈正相关，随流变系数增加而增大，这与式（36）表达的变化关系一致。

2）当n从0.7增大到0.9时，浆液压力损失变化不大；当n从0.9增大到1.1时，浆液压力损失有较大的增长。分析原因可能是当n＞1时，浆液表现为剪切稀化，当剪切速度增大时，浆液黏性增大，浆液压力减小，压力损失增大。

3）模拟中浆液压力损失随扩散距离的变化趋势与计算结果基本一致。在同一位置处，压力损失计算值比模拟值略小，且在注浆孔口处两者差值较小，随扩散距离增大而逐渐增大，但差值都在可接受范围内，可能是因为理论计算中未考虑裂隙表面的摩擦性，即未考虑裂隙壁对浆液流动的阻力造成的压力损失；且计算中未考虑浆液流动的惯性，即认为浆液完全是在浆液压力的驱动下流动。

4 工程借鉴

根据以上研究，为减少实际裂隙注浆工程中浆液压力的损失，增大浆液的扩散范围，确保较好的注浆加固效果，提出以下建议：

1）当浆液水灰比较大（W/C≥0.8），且浆液流量、浆液黏度、浆液屈服应力越大、裂隙开度越小时，浆液压力损失就越大，因此，在注浆时可适当地减小注浆速率，并通过添加外加剂等方式适当减小浆液黏度和浆液屈服应力。

2）当浆液水灰比较小（W/C≤0.7），且浆液流量、浆液稠度系数、浆液流变系数越大，裂隙开度越小时，浆液压力损失就越大，因此，在注浆时可适当地减小注浆速率，并通过添加外加剂等方式适当减小浆液稠度系数和浆液流变系数。

3）当裂隙开度较小时，应合理地控制以上参数。

5 结论

1）将水泥浆液分别视为牛顿流体、宾汉姆流体和幂律流体这3类流型的流体，并基于不同流体的本构方程与运动方程，用浆液压力损失作为分析浆液扩散情况的标准，推导出不同流型浆液的扩散方程。

2）牛顿流体浆液压力损失与流量q、黏度μ呈正比，与裂隙开度b的立方呈反比；宾汉姆流体浆液压力损失与流量q、黏度μ、屈服应力τ0呈正相关，与裂隙开度b呈负相关；幂律流体的浆液压力损失与流量q、稠度系数K、流变系数n呈正相关，与裂隙开度b呈负相关。

3）运用数值模拟软件，建立单一裂隙注浆模型，并通过定义不同流体，对不同流型浆液在裂隙中的扩散进行模拟研究。基于单一变量原则，建立不同工况，分析浆液压力与注浆参数的相关关系。

4）数值模拟和理论计算结果显示压力损失随浆液扩散距离的变化趋势基本一致。表明本文建立的浆液扩散方程和数值模拟模型能够很好地表述不同流型浆液在裂隙中扩散时浆液压力的分布及变化规律。

5）在实际注浆时，为减少浆液压力的损失，增大浆液的扩散范围，可适当减小注浆速率，并添加一定的外加剂，以便获得较好的注浆加固效果。