基于交替修正牛顿法的分布式传感器定位算法

徐莎莎， 周 芳

(1.桂林电子科技大学广西无线宽带通信与信号处理重点实验室， 桂林 541004； 2.桂林电子科技大学生命与环境科学学院， 桂林 541004)

无线传感器网络(wireless sensor network, WSN)是由大量的传感器节点构成的网络[1]，可以对指定环境进行实时监测。因其低成本、低功耗、体积小、多功能等诸多优点，无线传感器网络已经被广泛地应用于医疗(病人检测)、环境(大鸭岛实验)、家庭(用水检测)等领域[2-3]。其中大部分应用场景需要结合节点的位置信息，才能提供有效的数据信息。

目前，为了经济有效地实现WSN中的节点定位，通常在WSN中设置少部分位置已知的传感器节点，这部分位置已知的传感器节点安装了可以获取位置信息的全球定位系统(global positioning system, GPS)或中国北斗导航卫星系统(Beidou navigation satellite system, BDS)[4]，这些节点称为已知位置(location aware, LA)节点，又称锚节点，而其他需要定位的传感器节点称为未知位置(location unaware, LU)节点[2]。实现WSN中的节点定位还需获得测距信息，测距信息可以通过到达角(angle of arrival, AOA)、接收信号强度(received signal strength, RSS)、到达时间(time of arrival, TOA)和到达时间差(time difference of arrival, TDOA)等方式获得[5]。最后，结合锚节点位置信息和测距信息，采用协作定位方法定位LU节点[2]。

现有的大多数定位算法都假定锚节点位置准确，以便估计LU节点位置[2,6-8]。但在许多实际情况下，可能无法准确知道锚节点位置，这种不确定性反过来会显著地影响估计传感器节点位置的质量，水下WSN中的节点定位问题就是一个显著例子[9]。水下WSN节点分为三类：LU节点、锚节点和参考节点，锚节点和部分已经定位的LU节点可以组成参考节点。水下WSN中的节点定位目标是：利用锚节点和参考节点信息，采用协作定位方法定位LU节点。但射频波在水下会发生严重衰减，导致锚节点位置易出错和测距误差增大，从而产生较差的定位效果[10]。因此，考虑WSN中存在锚节点位置误差是一项很有意义的工作。

现有的定位算法基于运算方式不同可划分为两种。一种是集中式定位算法，集中式定位算法的运算特点是：融合中心进行位置估计时，需要获取所有范围内传感器节点之间的连接信息。Biswas等[8]将定位问题归结为集中式优化问题，然后，采用半正定规划松弛的方法，通过引入正则项减少优化变量的个数，并最终通过梯度下降法细化LU节点的位置，从而使得定位精度有所提高。但是，集中式定位算法随着WSN规模增大，通信代价也会变大，带宽会消耗过快，会导致整个WSN寿命缩短，无法适用于较大规模WSN。另一种是分布式定位算法，与集中式定位算法的运算方式相比，分布式定位算法的运算特点是：将处理器分布到每个传感器节点上，采用局部化处理的方式，更高效节能，更易扩展到较大规模WSN。Srirangarajan等[1]采用二阶锥规划松弛技术将定位问题转化为凸优化的问题，设计出了一种分布式算法，可适用于大规模WSN，但是该算法对于网络边界节点不能够很好定位，且需要更多的锚节点信息。Soares等[11]采用松弛非凸的最大似然估计条件，提出了一种简单凸松弛算法，并且每个节点采用梯度法达到收敛，从而降低了WSN的通信量。但是该算法要求LU节点在锚节点凸包之内才能保证良好定位效果。Zhou等[12]将WSN定位问题考虑成箱型约束下的欧式距离优化问题，提出了一种快速矩阵投影算法，有效地提高节点定位的速度。但是，该算法会使得误差累积和传播。上述定位算法具有很强适用性，易推广到处理锚节点位置误差影响定位精度这一优化问题。

为了克服锚节点位置误差影响定位精度这一问题，提出了基于交替修正牛顿法的分布式定位算法。首先，可将WSN看作一个无向图，特定区域内部署的传感器节点之间看作有一条边相连接，能相互通信。然后，将整个无向图划分成部分重叠的子图，这样全局的定位问题被划分成一系列的子图内定位问题。对于子图内定位问题的求解，提出了基于交替修正牛顿法的定位算法，其算法过程包含三个步骤：首先，LU节点根据不准确的锚节点和测距信息估计其位置，然后对部分重叠子图内的LU节点融合求平均，得到初步估计值；其次，不准确的锚节点根据LU节点初步估计值和测距信息更新其位置，再对部分重叠子图内的锚节点融合求平均，得到相对准确的锚节点位置；最后，LU节点再根据相对准确的锚节点位置和测距信息重复第一步步骤，得到最终估计值。仿真结果表明，当WSN存在锚节点位置误差时，相比较于现有的分布式定位算法，节点定位效果更好，且易适用于较大规模的WSN。

1 定位问题

N个传感器节点被随机分布在R2维空间的特定区域内，其中，有m个LA节和n个LU节点。所有准确位置的LA 节点表示为a1,a2,…,am，其在k点位置表示为ak=[xk,yk]T，所有LU节点表示为x1,x2,…,xn，其在i点位置表示为xi=[xi,yi]T。利用RSS测距技术能够测出传感器节点之间的距离[13-14]，但是，由于在此过程中易受到多径衰落等不确定因素影响，测得的数据往往是带噪声的。因此，假设LU节点xi和LU节点xj之间带噪声的欧几里得距离为dij，且dij=dji，LU节点xi和LA节点ak之间带噪声的欧几里得距离为dik。通常，在特定区域内，一定数量的传感器节点因受到功率的限制，不一定能够正常通信，因此，不是所有的传感器节点之间的欧几里得距离都可测得的，本文假设可测距的LU节点xi和LU节点xj的节点集合N为(i,j)∈N，可测距的LU节点xi和LA节点ak的节点集合M为(i,k)∈M[2,8]。wij和wik为根据带噪距离的反比取得的归一化权重[2,8]。这样可以将WSN全局定位问题归结为无约束优化问题[2,8]，可表示为

(1)

2 分布式定位算法

基于第1节定位问题的描述，正常通信的传感器节点之间是可以获取距离信息，根据距离信息，可以用无向图G=(V,E)表示WSN，其中，V(G)为传感器节点的位置，E(G)为传感器节点之间的连通性。基于传感器节点之间的连通性E(G)，将LU节点以及和其相连接的邻居节点所在的区域看作一个子图，从而将WSN表示的无向图划分成n个部分重叠的子图，重新建立起可以独立求解的子图内定位问题；然后，采用基于交替修正牛顿法的分布式定位算法，对子图内定位问题进行优化求解和局部融合。接下来，将分别从划分子图、子图内定位问题、子图内优化求解、算法总结进行详细描述。

2.1 划分子图

通过对式(1)的观察可知，LU节点位置只与通信半径R范围内的邻居节点和节点之间的距离有关[2]。因此，将LU节点视作中心节点，将与其构成邻居的节点组成无向图G的子图，这样，有n个LU中心节点则可划分成n个部分重叠的子图，这样做使得WSN的通信量和计算量能得到有效地降低，提高WSN的整体扩展性，使其易适用于较大规模的WSN。如图1所示，特定区域内随机分布部分传感器节点，以LU节点为中心，R为半径画一个虚线圆，一个虚线圆则表示一个子图。

(2)

式(2)中：Gs=(Vs,Es)为第s个子图，s=1,2,…，n，其中，Vs为第s个子图Gs内传感器节点的集合，Es为第s个子图Gs内传感器节点之间边的集合。

图1 子图划分示意图Fig.1 Schematic diagram of subgraphs division

2.2 子图内定位问题

基于子图Gs=(Vs,Es)包含的相关信息，通过最小化邻居节点之间距离误差的加权和[2,8]，将式(1)重新构建为一个无约束的子图内定位优化问题，可表示为

(3)

式(3)中：xsi为第s个子图内第i个LU节点位置，xsi=[xsi,ysi]T；xsj为第s个子图内第j个LU节点位置，xsj=[xsj,ysj]T；通常对流层误差、电离层误差、卫星钟差等误差容易影响锚节点位置[14]，因此，获取的锚节点位置很有可能是带噪声的，且不准确的，其带噪声模型如式(4)所示[1]，psk为第s个子图内第k个LA节点位置，psk=[xsk,ysk]T；Ns为第s个子图内可测距的LU节点xsi和LU节点xsj的节点集合；Ms为第s个子图内可测距的LU节点xsi和LA节点psk的节点集合；dsisj为子图内LU节点xsi和LU节点xsj之间带噪声的欧几里得距离；dsisk为子图内LU节点xsi和LA节点psk之间带噪声的欧几里得距离，其带噪声模型分别如式(5)、式(6)所示；wsisj和wsisk为子图内基于传感器节点之间带噪距离的反比取得的归一化权重[2]，其权重值可根据RSS测距技术特点得到，测距时，两个节点距离相距越远，噪声就越容易干扰到无线信号，得到的数据可信度越低，赋予的权重值越小，反之权重值越大[2,8]，wsisj和wsisk分别如式(7)、式(8)所示。

dsisj=‖xsi-xsj‖2|1+τ1εsisj|

(4)

dsisk=‖xsi-psk‖2|1+τ1εsisk|

(5)

psk=ask|1+τ2εsk|

(6)

(7)

(8)

式中：ask为锚节点真实位置；τ1∈[0,1]为锚节点位置噪声因子，作用是控制锚节点位置的噪声强度；τ2∈[0,1]为距离噪声因子，作用是控制测距之间的噪声强度；εsisj、εsisk和εsk为随机噪声，服从正态的随机变量N(0,1)。

(9)

(10)

式中：

A=(ei1-ej1)(ei1-ej1)T+(ei2-ej2)(ei2-ej2)T

(11)

(12)

(13)

(14)

(15)

则目标函数式(3)可以表示为

(16)

2.3 子图内优化求解

当WSN中存在锚节点位置误差时，LU节点基于不准确的锚位置和测距信息，采用协作定位算法定位出来的LU节点位置会估计误差较大。采用基于交替修正牛顿法的分布式传感器定位算法，确保当WSN存在锚节点位置误差时，能够更高精度地完成定位问题。基于交替修正牛顿法的分布式传感器定位算法包括：子图内估计LU节点、子图内更新LA节点、子图内融合。

2.3.1 估计LU节点

由式(16)可知，归结出来的子图内定位问题是关于LU节点位置xs和LA节点位置ps的高度非线性非凸的函数，因此，直接求解会比较比较困难。对此，因三边定位算法易于实现和维护，已被广泛应用于传感器定位领域[2,15-16]，采用三边定位算法得到一个初始值，以便可以快速地得到目标函数的局部最优解。然后，对于子图内定位问题，采用基于单位步长的交替修正牛顿法进行优化求解。

首先，在迭代优化之前，对式(16)进行一阶求导首先，对式(16)一阶和二阶求导，可得∇f(xs)和∇2f(xs)的表达式分别为

(17)

(18)

式中：Hessian矩阵∇2f(xs)不一定是正定的，无法保证算法中的牛顿方向为下降方向，算法可能会失败，解决Hessian矩阵∇2f(xs)非正定基本思想是：构建正定的∇2f(xs)，可表示为

DTps)(2Bxs-Cps-DTps)T]

[1]Laufer,B.&P.,Nation.(1999).A Vocabulary Size Test of Controlled Productive Ability,Language Testing,16(1).33-51.

(19)

从而能使用凸优化的求解方法进行优化求解，采用单位步长的修正牛顿算法估计LU节点。

算法1子图内估计LU节点

输入：xs0。

输出：xsi+1。

步骤1使用三边定位算法得到粗略的初始值xs0，设置i=0，表示第i次迭代，ω=1，步长ω为单位步长，迭代终止条件δ=1×10-9。

步骤2求目标函数式(16)的梯度向量∇f(xsi)和修正后的Hessian矩阵∇2f(xsi)。

步骤3计算搜索方向gsi=-∇2f(xsi)-1×∇f(xsi)。

步骤4沿着搜索方向gsi进行一维线性搜索，则xsi+1=xsi+ωgsi，不断更新子图内LU节点位置。

当WSN存在锚节点位置误差时，第2.3.1节子图内LU节点根据不准确的LA节点位置和测距信息，估计出来的LU节点坐标值存在较大的偏差。因此，将设计位置不准确的LA节点根据LU节点初步估计值和测距信息更新其位置，使得LA节点位置误差逐渐减小，从而得到相对准确的LA节点位置。这样，第2.3.1节LU节点再根据相对准确的LA节点位置和测距信息进行估计时，可以减小估计偏差。

首先，对式(16)先进行一阶求导，可得∇f(ps)的表达式为

(20)

然后，再进行二阶求导，可得∇2f(ps)的表达式为

(21)

(22)

然后，同2.3.1节一样采用基于单位步长的修正牛顿法迭代更新LA节点。

算法2子图内更新LA节点。

输入：ps0。

输出：psk+1。

步骤1根据2.3.1节优化求解的LU节点估计值，采用三边定位算法，粗略得到LA节点的估计值ps0，设k=0,表示第k次迭代，α=1,步长α为单位步长，迭代终止条件η=1×10-9。

步骤2求目标函数式(16)的∇f(psk)和修正后的∇2f(psk)。

步骤3计算搜索方向dsk=-∇2f(psk)-1×∇f(psk)。

步骤4沿着搜索方向更新子图内LA节点位置，psk+1=psk+αdsk。

2.3.3 子图融合

划分子图时，将WSN表示的无向图G=(V,E)，以LU为中心划分成n个部分重叠的子图Gs=(Vs,Es)，s=1,2,…,n。如图1所示，各个子图内在独立优化求解节点位置时，不同子图内，同一个节点被估计出来的位置都是不相同的，这将导致某个子图内信息利用较少，也导致优化求解的节点位置误差较大。为了有效地降低这部分误差，促进子图之间的协作定位，提高整体定位精度，采用融合求平均的方式，对该节点在不同子图内的节点位置求平均，即

(23)

(24)

2.4 分布式算法总结

当WSN中存在锚节点位置误差时，所提的分布式定位算法中，首先，将LU节点视为中心节点，以及其邻居节点所在的区域为子图，将全局的定位问题重新构建为多个子图内定位问题。一方面，对于子图内定位问题的求解，采取交替修正牛顿法进行优化求解，通过不断地交替估计LU节点位置和更新LA节点位置，使得LA节点位置误差逐渐地减小，进而可以有效地降低LU节点位置估计误差。在算法迭代开始之前，采用易于维护和实现的三边定位算法得到LU节点初始位置，目的是确保估计节点位置时能不断地接近局部最优解，确保搜索方向是沿着子图内目标函数的下降方向，并使得子图内目标函数能够尽快地收敛。另一方面，同一个节点会被包含在多个子图内，会优化求解得到不同的估计位置，因此，对部分重叠子图内的节点采用融合求平均的方式，在一定程度上，对子图内定位误差较大的节点进行修正，使其获得一个较好的初始值参与下一步的迭代。总之，通过不断地重复对子图内节点优化求解和融合求平均这两个步骤，可以有效地利用子图之间协作定位的特点，确保当WSN存在锚节点位置误差时，能够更高精度的完成定位任务。

综上所述，WSN存在锚节点位置误差的情况下，基于交替修正牛顿法的分布式定位算法如下。

步骤1将n个LU节点，m个LA节点随机部署在[-0.5,0.5]2的单位正方形区域内，通信半径设为R，把WSN以LU节点为中心划分n个部分重叠的子图，n个子图内分别可以进行分布式运算。令t=0，终止条件β=1×10-2。

3 实验结果及分析

为了表明本文算法的定位性能，给出了4个仿真实验。使用软件MATLAB 2017b来仿真实验，并运行在Intel i7-7700主频3.6 GHz的PC。为表明算法的鲁棒性，所有的仿真实验都是5次取平均，定位区域均为[-0.5,0.5]2。为了客观真实地评估所提的分布式定位算法的性能，采用与文献[8,12,15]的评价指标，即根均方距离(root mean square distance, RMSD)，其表达式为

(25)

图2 不同LA节点数目下各算法的平均RMSDFig.2 The average RMSD of each algorithm under different number of LA nodes

3.1 实验1

为了研究WSN存在锚节点位置误差时，锚节点数目在WSN中所占比例对定位精度的影响，本文算法与文献[1,11-12]中的分布式定位算法做对比实验。本次实验中，设置节点总数N=200，锚节点位置噪声因子τ1=0.10，距离噪声因子τ2=0.10，WSN中通信半径R=0.30，将WSN中锚节点所占比例p从0.10增加到0.30。实验结果如图2所示，可以看出，随着WSN中锚节点数目所占比例p的增加，本文算法和文献[1,11-12]算法的RMSD均在降低，定位精度得到提高。但是与文献[1,11-12]算法相比，本文算法在不同锚节点所占比例下，RMSD明显小于对比的三篇文献所提算法的RMSD，本文算法的定位精度更高。分析其原因是：随着WSN中的锚节点数目增多，LU节点会获得更多邻居的相关信息，从而得到一个更好的初始值参与下一步迭代，使得定位精度得到提高。这意味着：当大规模WSN存在锚节点位置误差时，本文算法可以使用较少的锚节点数目实现更好的定位效果，有效地降低了WSN的部署成本。

3.2 实验2

为了研究WSN存在锚节点位置误差时，WSN中通信半径R对定位精度的影响，本文算法与文献[1,11-12]中的分布式定位算法做对比实验。本次实验中，设置节点总数N=200，锚节点位置噪声因子τ1=0.10，距离噪声因子τ2=0.10，WSN中的锚节点所占比例p=0.15，将WSN中通信半径R从0.22增加0.30。实验结果如图3所示，可以看出，随着WSN中通信半径R增加，本文算法和文献[1,11-12]算法的RMSD均在增大，定位精度均在降低。但是与文献[1,11-12]算法相比，本文算法的RMSD在不同R下始终保持最小，本文算法的定位精度高于文献[1，11-12]算法。分析其原因是：随着通信半径R增加，WSN的通信量和计算量也会随之增大，相应的也会影响定位性能。这意味着：当大规模WSN存在锚节点位置误差时，本文算法可以使用较小通信半径R实现更好的定位效果，能够减少传感器通信时的能量消耗，提升整体WSN的寿命。

3.3 实验3

为了研究WSN存在锚节点位置误差时，不同传感器网络规模情况下的定位效果，固定WSN中锚节点所占比例p=0.15，锚节点位置噪声因子τ1=0.10，距离噪声因子τ2=0.10，本文算法与文献[1,11-12]算法在改变总节点数目N，通信半径R下进行仿真实验，仿真参数具体设置和实验结果如表1所示。分析可知：随着WSN中总节点数目N不断地增大，在相同的仿真参数下，本文算法与文献[1,11-12]算法相比较，本文算法的RMSD更小，定位精度更高，进而定位性能更好。这表明当大规模WSN存在锚节点位置误差时，本文算法具有较好的扩展性，能够有效地应用于较大规模的WSN，并且具有较高的定位精度。

图3 不同通信半径下各算法的平均RMSDFig.3 The average RMSD of each algorithm under different communication radius

表1 各定位算法5次仿真所得的定位结果Table 1 The localization results obtained from 5 simulations of each localization algorithm

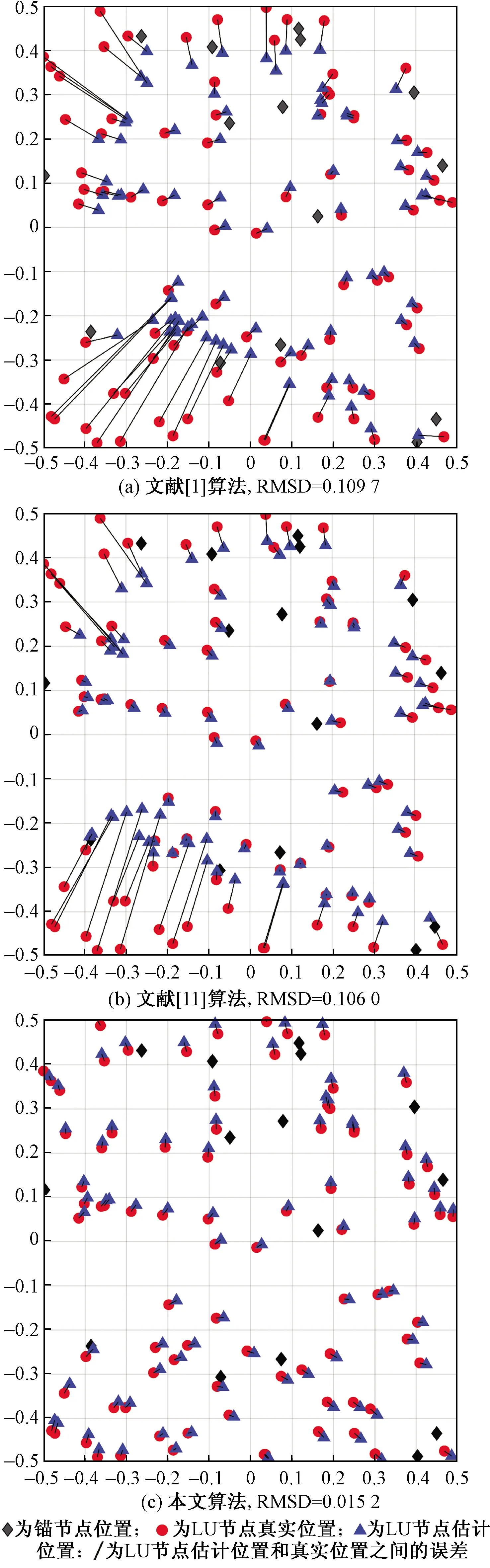
图4 不同算法在随机拓扑中的结果Fig.4 The results of different algorithms in random topology

3.4 实验4

为了研究节点分布的方式以及仅存在锚节点位置误差时对定位精度的影响。仿真参数设置如下：定位区域为[-0.5,0.5]2，节点数目N=100，锚节点所占比例p=0.15，锚节点位置噪声因子τ1=0.10，通信半径R=0.40，并将实验结果可视化。本次实验与文献[1,11]算法相比较，仿真结果如图4、图5所示，图4展示的是传感器节点随机分布在指定区域，图5展示的是传感器节点分布在C型拓扑中。从实验结果可以看出，在不同的分布形式，相同的仿真参数下，本文算法相比较文献[1,11]算法，对分布区域的边界节点展现较好的定位效果，RMSD都比较低，有较高的定位精度。这表明当WSN存在锚节点位置误差时，本文算法能在不同分布式形式下展现较好的定位效果。

图5 不同算法在C型拓扑中的结果Fig.5 The results of different algorithms in type C topology

4 结论

为了克服锚节点位置误差影响定位精度这一问题，提出一种基于交替修正牛顿法的分布式定位算法。首先，将WSN划分为多个部分重叠的子图，建立可以独立求解得到子图内优化问题。然后，通过本文算法对子图内定位问题进行优化求解。仿真实验表明，本文算法在WSN存在锚节点位置误差的情况下，能对较大规模WSN实现精确定位，可见本文算法具备一定的优势，可以为无线传感器网络在环境科学、水下定位等领域提供技术上的支持。后续工作会在提高定位精度的同时，考虑异步的分布式算法。