基于深度学习的激光同步定位与地图构建移动机器人可定位性研究

高 扬， 张传玺， 王 晨， 王书棋

(长安大学汽车学院， 西安 710064)

定位是机器人进行导航、运动等任务的基础，其定位精度也直接影响相关任务的执行效果。目前移动机器人领域常用的定位手段包括卫星定位、惯性导航、地图匹配、航迹推算等。可定位性是指移动机器人获得准确定位的难易程度，也指定位误差的大小[1]。可定位性估计，作为机器人领域的一个较新的问题，并利用其评估结果成功控制机器人获得了良好效果。汪志刚等[2]提出了一种紧耦合的视觉惯性组合定位方法，该方法准确率较高，但易受室内亮度的影响，鲁棒性较差。Zhen等[3]提出了一种融合惯性测量单元(inertial measurement unit，IMU)和旋转激光扫描仪测量的鲁棒定位方法，并提出一种评估给定三维地图可定位性的新方法，但该方法计算复杂度较高。Ferreira等[4]为了研究水下定位问题提出基于启发式算法的自适应信息融合神经网络框架(behaviors-prediction reliability-fusion，B-PR-F)，该框架在融合信息之前对单个估计的置信度进行评估。Alomari等[5]介绍了一种用于无线传感器中移动锚辅助定位的静态路径规划模型。与类似的静态模型相比，该模型能较好地估计其位置，具有较高的定位精度。周奇勋等[6]设计了一种基于被动式移动架构的定位系统，该系统定位精度较高，但须安装定位基站，实现较为复杂。赵妍等[7]提出了一种基于同时定位与地图创建技术的机器人智能激光定位技术，该方法收敛性较好，但精度不高。苗润龙等[8]提出了一种基于最小二乘高斯核支持向量机的单目视觉定位算法，该算法利用最小二乘高斯核支持向量机,将机器人在图片中像素位置与真实场景中位置间的非线性映射转化为带高斯核的线性映射，算法精度较优，但选参优化过程过于复杂。Wu等[9]提出了一种高效的分布式方法，该方法在时延和定位检测精度方面都优于现有的算法。Xia等[10]提出了一种基于刚度理论的无线传感器网络可定位性判断方法。Li等[11]提出了一种利用地图辅助水平不确定度(map aided horizontal uncertainty level，MA-HUL)来测量定位系统所提供信息置信度的方法。为了提高定位的可靠性，Fankhauser等[12]提出了一种新的地形测绘方法，但该方法只基于运动和惯性测量的主体感知定位。Le等[13]描述了基于梯度下降的运动规划器，试图优化或约束网络可定位性变化的机器人，此外该方法须考虑移动机器人网络部署问题，较为复杂。Luo等[14]提出了一种基于网格的室内协同定位跟踪算法(cooperative localization and tracking algorithm，CLTA)，该算法在定位跟踪性能上优于单网络定位算法，精度较高，效率一般。

综上，针对目前常用的地图匹配定位方法，现有可定位性估计方法难以直接、准确、高效地估计可定位性，在场景应用中与实际定位误差相比仍存在一定误差[15]。因此如何实现对可定位性的更准确评估仍然是一大难点问题。基于激光扫描仪针对常用的地图匹配定位算法的可定位性展开研究，现提出一种新颖的基于深度学习的可定位性估计方法估计定位熵评价可定位性。

1 方法

经典的地图匹配定位算法中，定位信息来源于航迹推算与地图匹配两个部分，其中航迹推算部分中关于位姿估计的不确定性[15]已进行了分析，不再赘述。对采用激光扫描仪扫描周围环境实现定位的地图匹配部分，现对其定位误差分析如下。

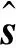
ri(s)=f(s,θi)+ε

(1)

式(1)中：ε为一维0均值高斯观测噪声；f为一种函数映射关系。

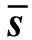
(2)

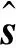
(3)

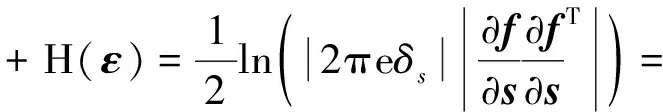
(4)

(5)

式中：H(·)为求熵函数。

由于机器人的定位过程实际上是由一帧激光内所有观测得到的位姿估计融合的结果。故依据信息融合理论，对同一状态的估计，假设各估计间相互独立，则有融合单帧内所有观测结果后的熵可表示为

(6)

式(6)中：N为单帧激光探测值的数据点总数量。

2 多模块深度神经网络

估计定位熵公式[式(5)]仍然过于复杂且存在信息压缩，难以直接计算融合定位熵，因此本文结合信息融合理论，提出一种基于深度学习的多模块神经网络结构(multi-module-networks，MMN)以预测机器人定位熵值。

图2 卷积神经网络CNN结构Fig.2 CNN structure of convolutional neural network

考虑到定位结果来源于地图匹配与航迹推算结果的融合，设计的MMN(图1)同样由3个模块构成：地图匹配定位熵估计模块，采用卷积神经网络(convolutional neural network，CNN)；航迹推算定位熵估计模块，采用长短期记忆网络(long short-term memory，LSTM)；融合熵估计模块，采用多层全连接网络(multi-layer full connection，MLFC) 。t时刻激光探测值X1(t)输入地图匹配定位熵估计模块得到输出特征t时刻估计熵值S1(t)，其中X1(t)为t时刻激光数据，大小为1×1 080。激光探测值X2(t)、X3(t)、S(t-1)输入航迹推算定位熵估计模块得到输出特征t时刻估计熵值S2(t)，X2(t)为t-1～t时刻机器人位移；X3(t)为t-1～t时刻机器人转过角度；S(t-1)为t-1时刻机器人定位熵值，将两个模块输出特征S1(t)，S2(t)输入融合熵估计模块输出t时刻融合熵值S(t)，S(t)为t时刻机器人定位熵值。

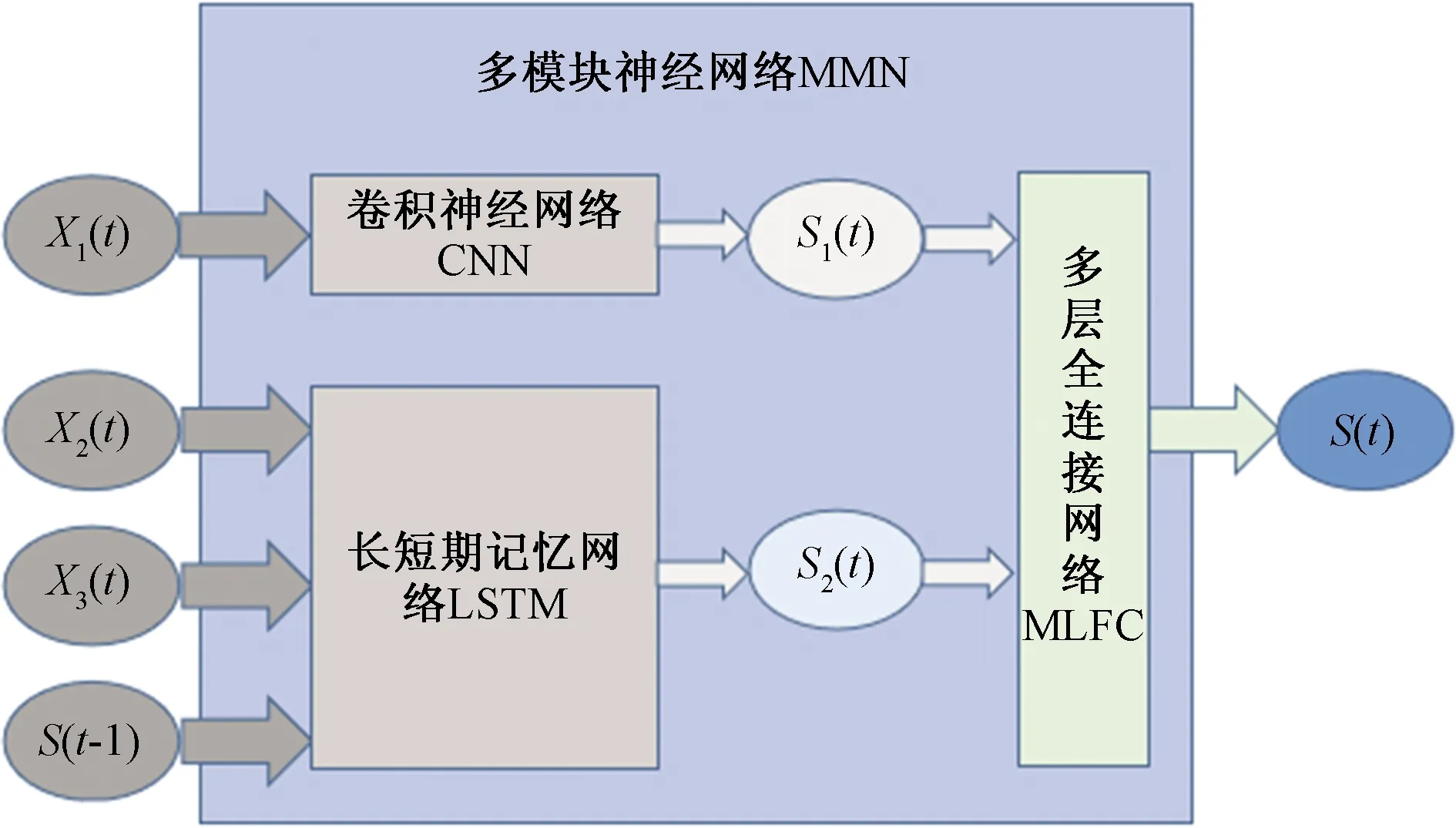
图1 多模块神经网络MMN结构Fig.1 Multi-module neural network MMN structure

2.1 地图匹配定位熵估计模块

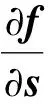
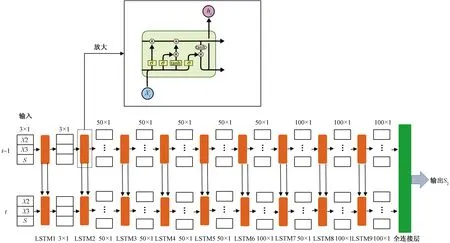
σ为sigmoid激活函数，该函数输出为0～1；tanh为双曲正切激活函数，输出为-1～1；ht为t时刻隐层状态图3 长短期记忆网络LSTM结构Fig.3 LSTM structure of long short-term memory network

2.2 航迹推算定位熵估计模块和融合熵估计模块

由于机器人的定位熵值与前一时刻机器人的角速度，线速度有关，所以为航迹推算定位熵估计模块设计了长短期记忆神经网络，该网络以t-1～t时刻间机器人的线位移，角位移与t-1时刻机器人定位熵值作为输入，t时刻机器人定位熵作为输出预测机器人定位熵。如图3所示，共设计10层隐层，前9层为9个长短期记忆(long short-term memory，LSTM)层，第一层输出3×1向量，第2～6层输出50×1向量，为了防止训练过程过拟合，第十层采用丢失率为0.2的Dropout层。最后输出层采用线性回归函数Linear作为激活函数，得到LSTM网络估计航迹推算定位熵S2。

为融合熵估计模块设计了多层全连接网络MLFC以融合地图匹配定位熵估计模块与航迹推算定位熵估计模块的结果。如图4所示，S1、S2、S分别为CNN网络预估地图匹配定位熵，LSTM网络估计航迹推算定位熵，以MLFC估计前两者融合后的定位熵，该网络设计了5个隐层，前2个隐含层设计256个神经元，第3和第4隐含层各设计128个神经元，第5个隐含层设计64个神经元，每层的激活函数为线性整流函数，输出层有一个神经元，激活函数为线性回归函数。

3 实验研究

3.1 数据集说明

针对常见的室内外环境进行了数据采集以制作样本库，如图5所示，数据采集平台采用先锋P3DX机器人以及Hokuyo UTM-30型激光雷达，该激光雷达的扫描角度范围为270°，角分辨率大小为0.25°，最大检测距离为3 m。激光数据分布如表1所示。定位算法采用AMCL(adaptive Monte Carlo localization)算法。每组数据内容包括时间戳、激光扫描数据、线速度、角速度、定位熵。

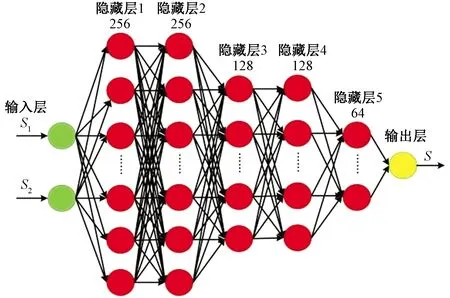
图4 多层全连接神经网络MLFC结构Fig.4 Multi-layer fully connected neural network MLFC structure

图5 数据采集平台Fig.5 Data collection platform

将整个数据集分成A、B两个子数据集，分别用于卷积神经网络和循环神经网络的训练。子数据集A由激光扫描数据和定位熵组成，分别作为地图匹配定位熵估计模块的输入和输出。子数据集B由线位移、角位移和定位熵组成。以当前线位移、角位移及上一时刻定位熵为长短期记忆神经网络输入，当前时间戳定位熵为该网络输出。

整个数据集定位熵值域范围为[-11.57，10.46]，以间隔1将值域划分为23个区间，则数据集中定位熵在各区间的分布如图6所示。将整个数据集划分为训练集占比64%，验证集16%，测试集占比20%。

表1 激光数据分布Table 1 Laser data distribution

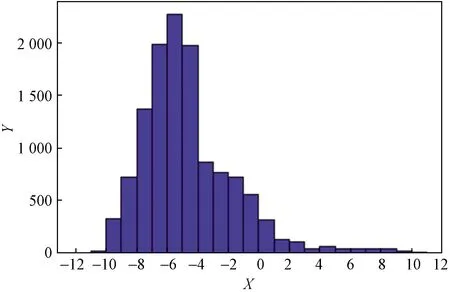
X为熵值；Y为该区间内熵值数量图6 熵值分布Fig.6 Entropy distribution

3.2 训练及测试结果

为提高多模块神经网络结构对定位熵估计的准确性，分别训练地图匹配定位熵估计模块，航迹推算定位熵估计模块，其次在两个网络权重基础之上进行总体网络的训练。采用Nvidia公司GTX2080TI显卡进行训练与测试。

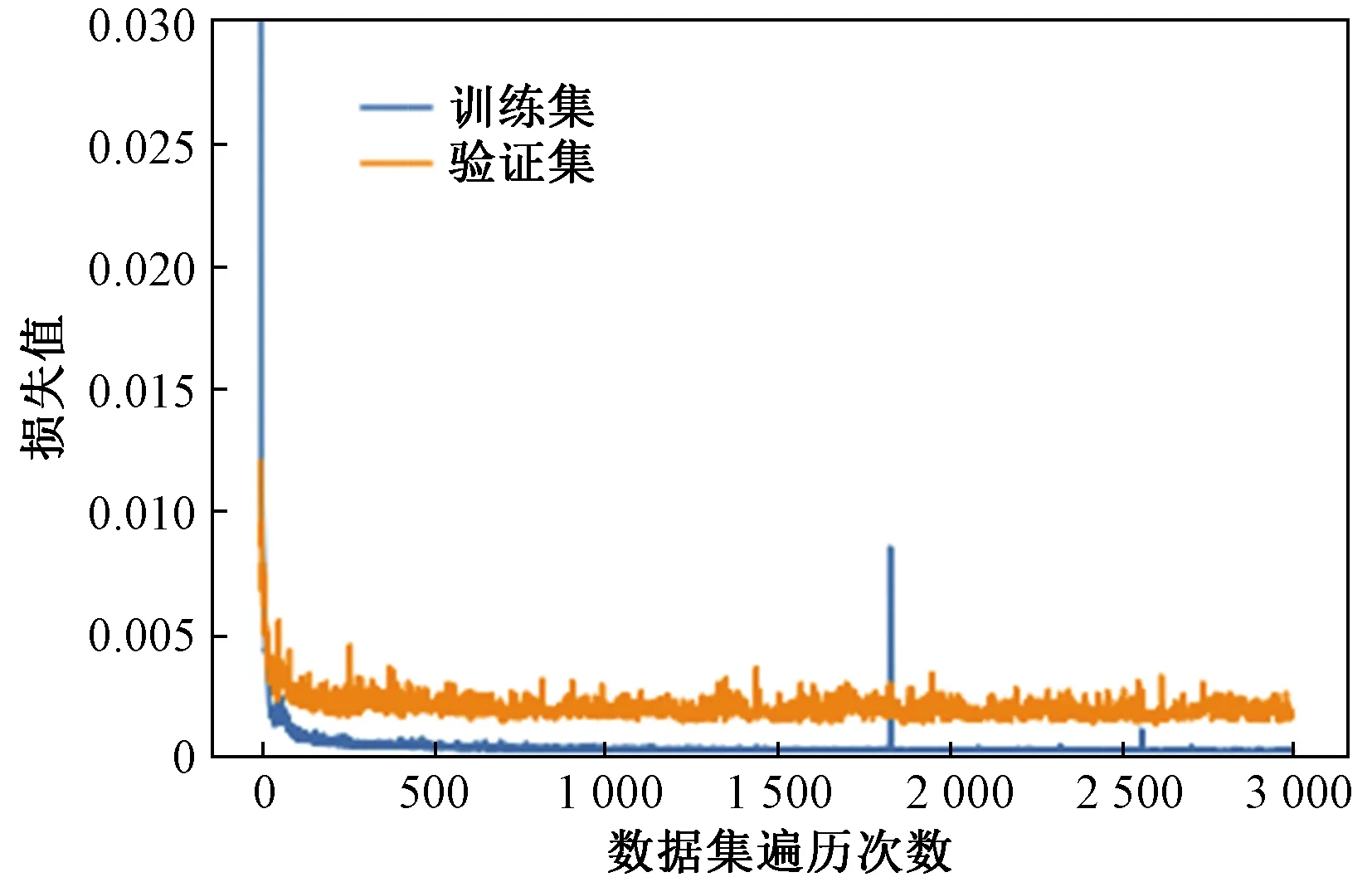
图7 地图匹配定位熵估计模块Loss曲线Fig.7 Map matching location entropy estimation module Loss curve

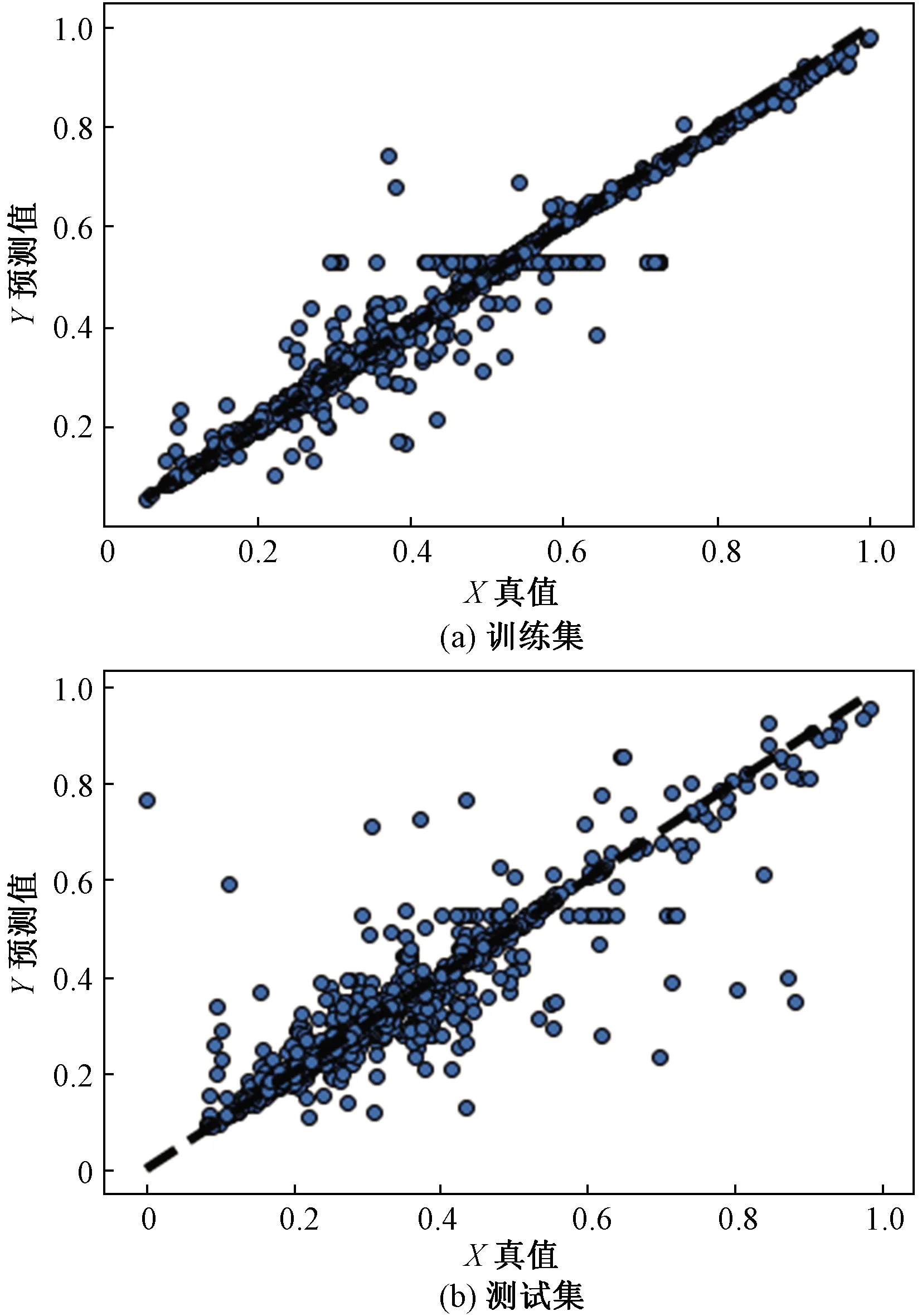
X为AMCL算法测得的真值；Y为本文算法预测所得的熵值图8 地图匹配定位熵估计模块训练集和测试集结果Fig.8 Map matching location entropy estimation module training and testing set results

地图匹配定位熵估计模块训练参数设置为：batch_size为20，epoch为3 000，learning_rate为0.002，损失函数Loss采用均方误差，优化器选择adamax。图7为地图匹配定位熵估计模块训练Loss曲线，可以看出，当epoch数值为500时，网络训练集与验证集loss趋于稳定。图8为子集A中训练集与测试集定位熵的真实值与预测值的对比。训练集的平均Loss为0.000 26，测试集的平均误差为0.002 38，训练效果良好。

航迹推算定位熵估计模块训练参数设置为：batch_size为20，epoch为3 000，learning_rate为0.002，损失函数Loss采用均方误差，优化器选择adamax。图9为航迹推算定位熵估计模块Loss曲线，可以看出,当epoch数值为500时，网络训练集与验证集Loss趋于稳定。图10为训练集与测试集定位熵的真实值与预测值的对比，训练集的平均Loss为0.000 72，测试集的平均误差为0.000 67，训练效果良好。

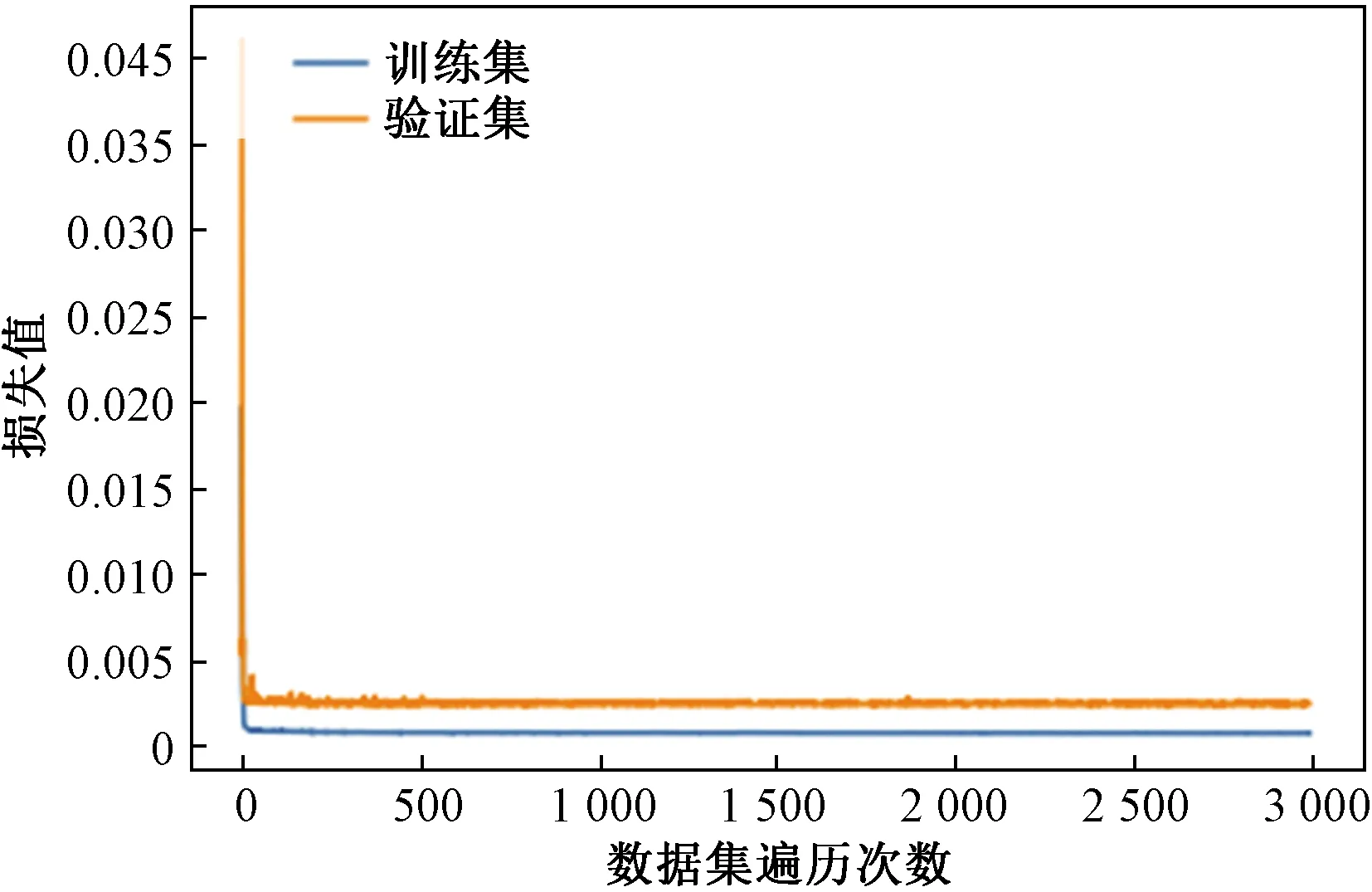
图9 航迹推算定位熵估计模块Loss曲线Fig.9 Dead reckoning location entropy estimation module Loss curve

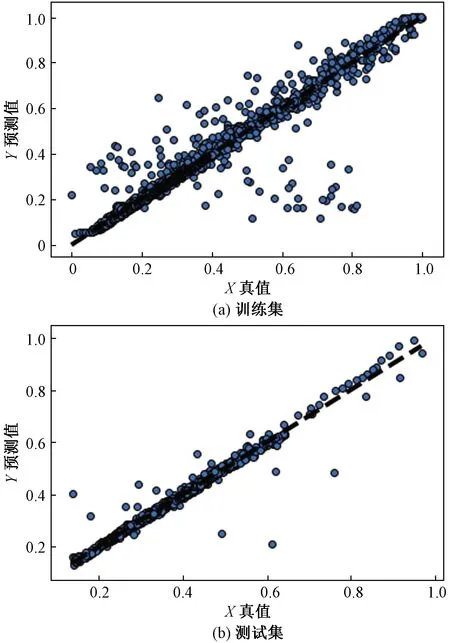
X为由AMCL算法测得的真值；Y为由本文算法预测所得的熵值图10 航迹推算定位熵估计模块训练集、测试集结果Fig.10 Dead reckoning location entropy estimation module training and testing set results

融合熵估计模块训练参数设置如下：batch_size为20，epoch为3 000，learning_rate为0.002，损失函数Loss采用均方误差，优化器选择adamax，加载权重为CNN与LSTM训练权重。由图11可以看出，当epoch数值为500时，网络训练集与验证集Loss趋于稳定。图12为训练集与测试集定位熵的真实值与预测值的对比，训练集的平均Loss为0.000 27，测试集的平均误差为0.000 57，训练效果良好。

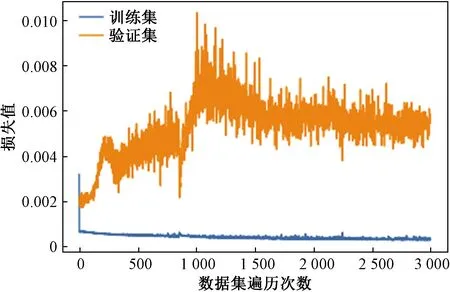
图11 融合熵估计模块 loss曲线Fig.11 Fusion entropy estimates the module loss curve

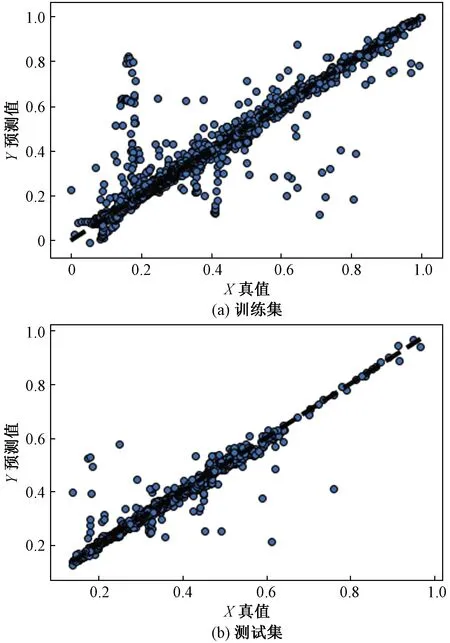
X为由AMCL算法测得的真值；Y为本文算法预测所得的熵值图12 融合熵估计模块训练集、测试集结果Fig.12 Fusion entropy estimation module training and testing set results

为进一步验证多模块网络MMN的准确性与鲁棒性，在图13占据栅格地图所示的新室内环境中进行实际实验验证，实验结果如图14所示，横坐标表示由AMCL算法实际测得的真值，纵坐标表示由本文算法预测所得的熵值，两者平均误差为0.003 5，预测熵值与实测熵值相比误差小于5%，结果表明所设计MMN模块在新环境下估计的定位熵值与真实值较为接近。

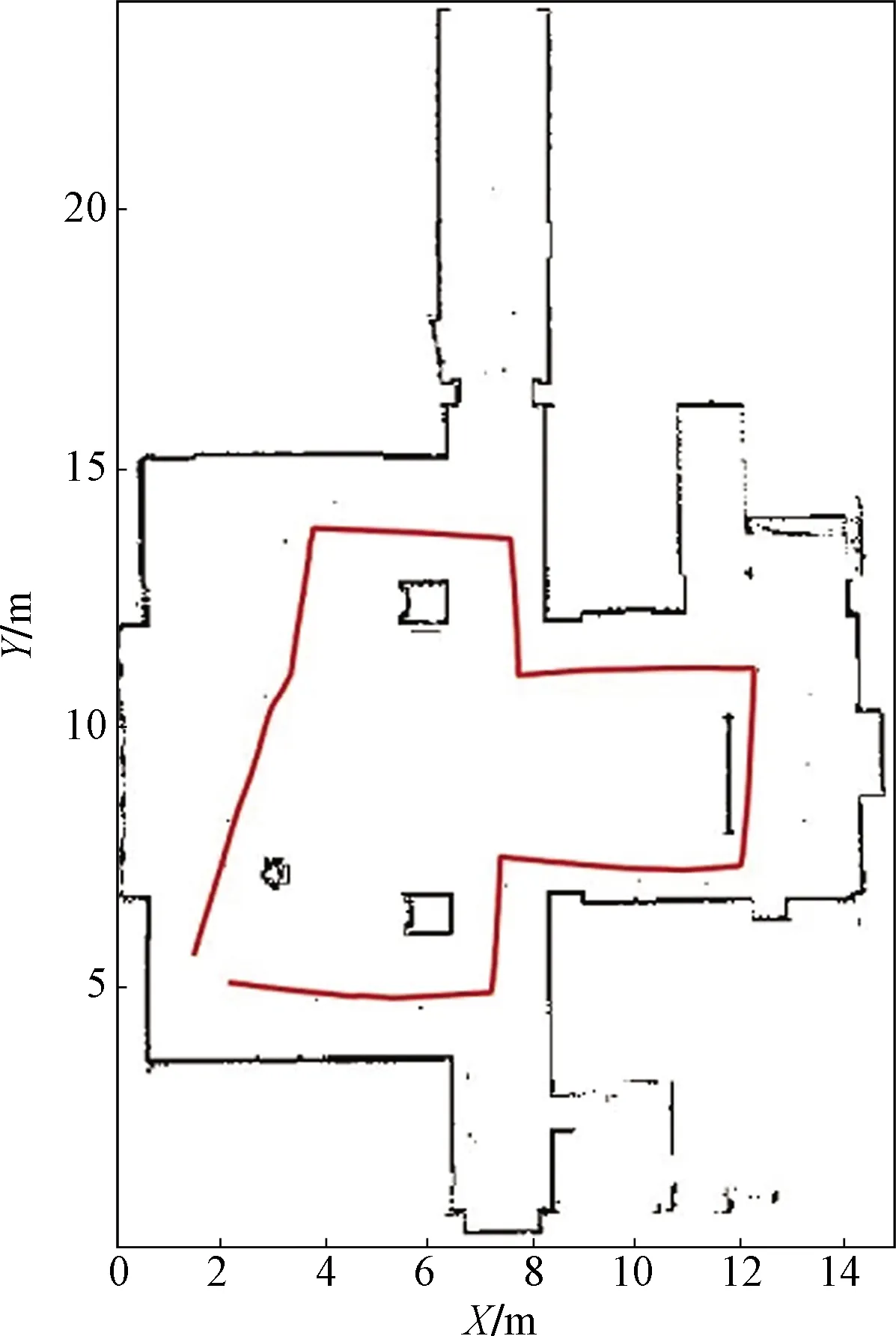
红色部分为机器人在6 min内的运动轨迹图13 实验环境Fig.13 Experimental environment

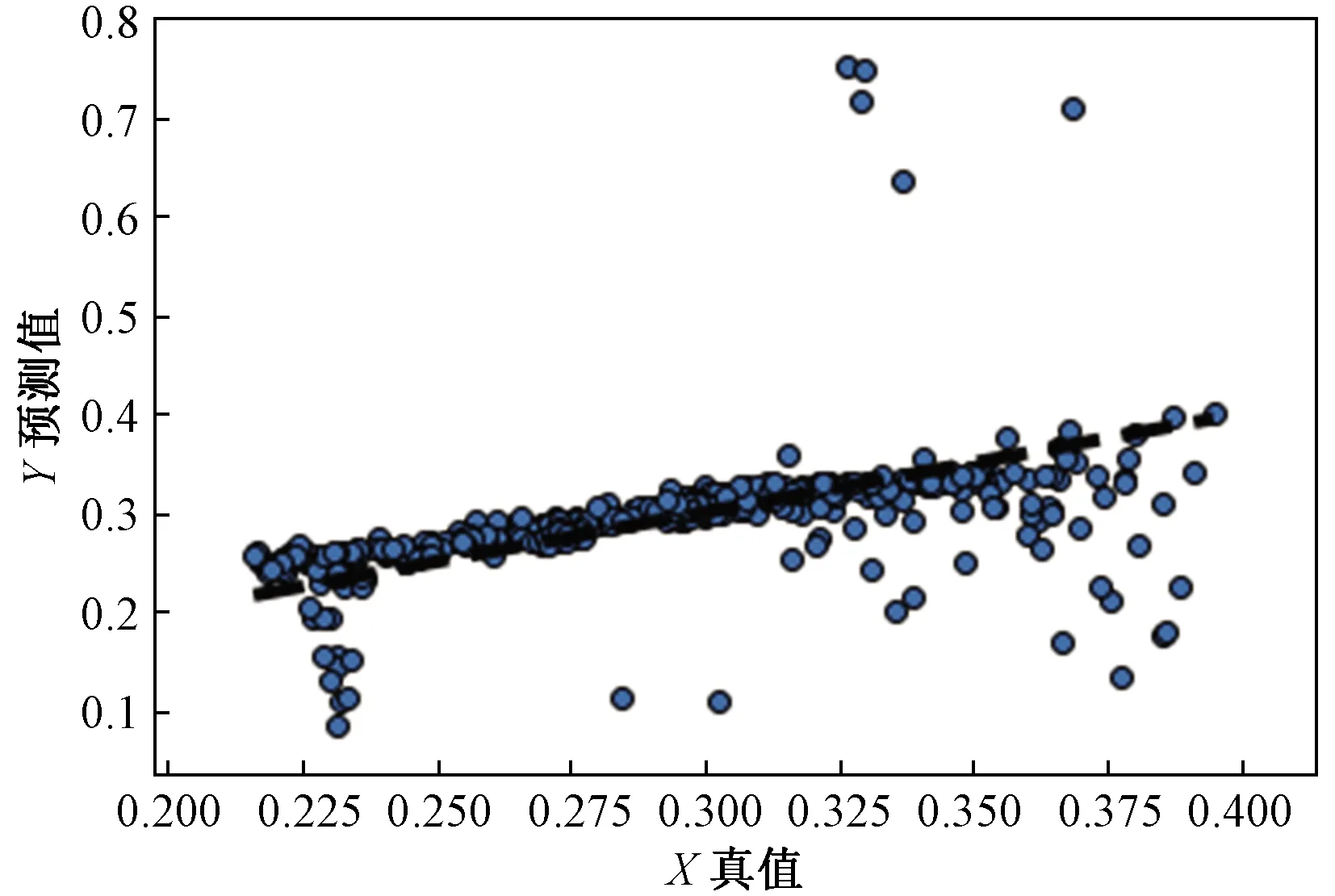
图14 新环境实验结果Fig.14 Experimental results of new environment

4 结论

基于地图匹配的定位算法中定位误差来源的基础上，提出以定位熵作为可定位性评价指标，设计了一种新颖的多模块神经网络模型估计定位熵值，该方法通过融合多模块熵值结果可以对定位熵进行高效、准确估计，完成机器人在复杂环境下自定位，对未来机器人领域乃至自动驾驶领域可定位性估计具有一定的参考价值。