基于向量式有限元的岸桥动力学分析

王嘉诚， 刘 龙

(上海海事大学上海离岸工程研究院， 上海 201306)

岸边集装箱起重机是在码头进行货物装卸的重要机械。在起重机的工作过程中小车的运行与吊重的偏摆会导致结构发生弯曲变形与振动，结构的振动又会反过来影响小车与吊重，对起重机的运行安全与工作效率产生影响。因此对工作状况下的岸桥进行动力学分析是有必要的。

移动物体作用下的耦合系统通常简化为移动质量-大梁系统进行分析。秦仙蓉等[1]进行了不同运动参数的移动质量作用下的简支梁动力学响应分析。段民封等[2]提出了针对不确定性移动载荷激励下的简支梁分析方法。龚云轩等[3]基于Timoshenko阶梯梁模型，分析了移动质量作用下梁的振动响应。Zhang等[4]对移动载荷作用下的Euler-Bernoulli梁与Timoshenko梁的响应进行了对比。Qiao等[5]研究了黏弹性边界条件下梁的振动响应。经薇等[6]研究了多个车辆作用下的车桥耦合振动特性。

与车桥耦合系统不同的是岸桥结构复杂并且需要考虑吊重的作用。苏晴等[7]建立了岸桥上部结构简化模型，将拉杆模拟为弹簧支撑，门架连接处假设为简支边界条件。刘华森等[8]建立了简支梁、移动小车与吊重的耦合系统并进行数值求解。Wu等[9]将吊重假设为考虑吊具的双摆与单摆两种形式，把结果进行对比。辛运胜等[10]考虑了轨道缺陷，建立司机-起重机-轨道系统进行分析。

向量式有限元(vector form intrinsic finite element，VFIFE)是一种新型数值计算方法。Long等[11]进行了空间框架结构在地震作用下的倒塌模拟。唐敬哲等[12]基于有限质点法对界面之间的接触、断裂等行为进行了分析。Duan等[13]进行了考虑车钩效应的车桥耦合问题分析。

前人研究中进行起重机小车运行工况下的分析时，将桥式和门式起重机简化为简支梁，针对结构复杂的岸桥则需要对模型进行简化处理。现基于向量式有限元理论，建立包含单元耦合、铰接点和质量点的岸桥模型，对移动吊重与小车作用下的岸桥动力学行为进行分析，解决在岸桥的动力学分析中如何表示单元间耦合与铰接点的问题，摆脱目前依赖有限元软件进行分析的现状。

1 向量式有限元理论概述

向量式有限元与经典力学的区别在于对结构概念的描述和简化的方式不同。向量式有限元理论由3个基本概念组成，分别为点值描述、途径单元和虚拟的逆向运动。

1.1 梁单元理论

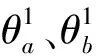
(1)

令t2时刻的杆单元a2b2做虚拟的逆向运动，首先进行逆向的平移-u，使得节点a2与a1的位置重合，此时杆单元到达虚拟位置的两端节点为a′2和b′2。之后再进行逆向的转动-Δθ，使得单元a′2b′2与单元a1b1平行，到达虚拟位置的两端节点为a″2和b″2，转角的大小为Δθ=sin-1|e1e2|，其中u′b、u″b、u‴b和u‴a分别为节点b1～b′2、节点b′2～b″2、节点b1～b″2和节点a1～a″2的位移。逆向运动后节点的位移与转角变化为

(2)

图1 梁单元的虚拟逆向运动Fig.1 Virtual reverse motion of beam element

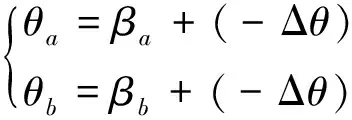
(3)

根据虚功原理，因节点变形导致的节点内力做功与单元的变形虚功相等。对单元进行分析后可得t1与t2时刻的节点内力的差值为[14]

(4)

式(4)中：I为惯性矩；A为截面面积；E为弹性模量；Δfbx为节点b所受内力的插值；Δma和Δmb分别为节点a和b所受弯矩的差值；Δ为单元的纯变形，θa和θb分别为节点a和b的转角。

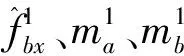
(5)

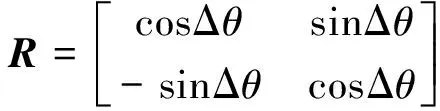
(6)

则单元内力的表达式为

(7)

图2 梁单元节点内力Fig.2 Internal forces of beam element points

式(7)中：fjx、fjy和mj分别为全局坐标下的单元在x方向上的内力、y方向上的内力和弯矩，单元作用在两端节点上的内力为单元内力的反作用力，因此节点a和b所受内力分别为fa=fa，fb=-fb。取Pa和Pb为两个节点所受外力，节点所受合力Fa=Pa+fa，则梁单元节点运动表达式为

(8)

式(8)中：Ma为质量矩阵；xa为位移矩阵;Fa为合力矩阵；ma和Ia分别为节点的质量和惯性矩；xa、ya和θa分别为节点a水平与竖直方向位移与转角；Fax、Fay和Faz为3个方向上的力。

使用中心差分法，将式(8)代入中心差分公式中，可得第-1步、第1步和第n+1步的节点a的位移迭代公式分别为

(9)

(10)

(11)

根据牛顿运动定律可知在没有消能机制的情况下，振动的物体将保持持续振动的状态。所以在运动公式中加入阻尼力，起到减小振动的振幅的作用，以此得到近似的收敛结果。

1.2 杆单元理论

对于桁架机构、连杆机构等轴力杆件结构可使用向量式有限元杆单元理论进行模拟。向量式有限元杆单元与梁单元的不同之处在于不考虑节点的转动，与之对应的内力与外力中减少弯矩的作用。

杆单元求解节点内力的思路与梁单元理论类似，通过虚拟的逆向运动得到单元的纯变形。结构如图1所示，由材料力学知识可得，t2时刻的杆单元a2b2两端节点内力为

(12)

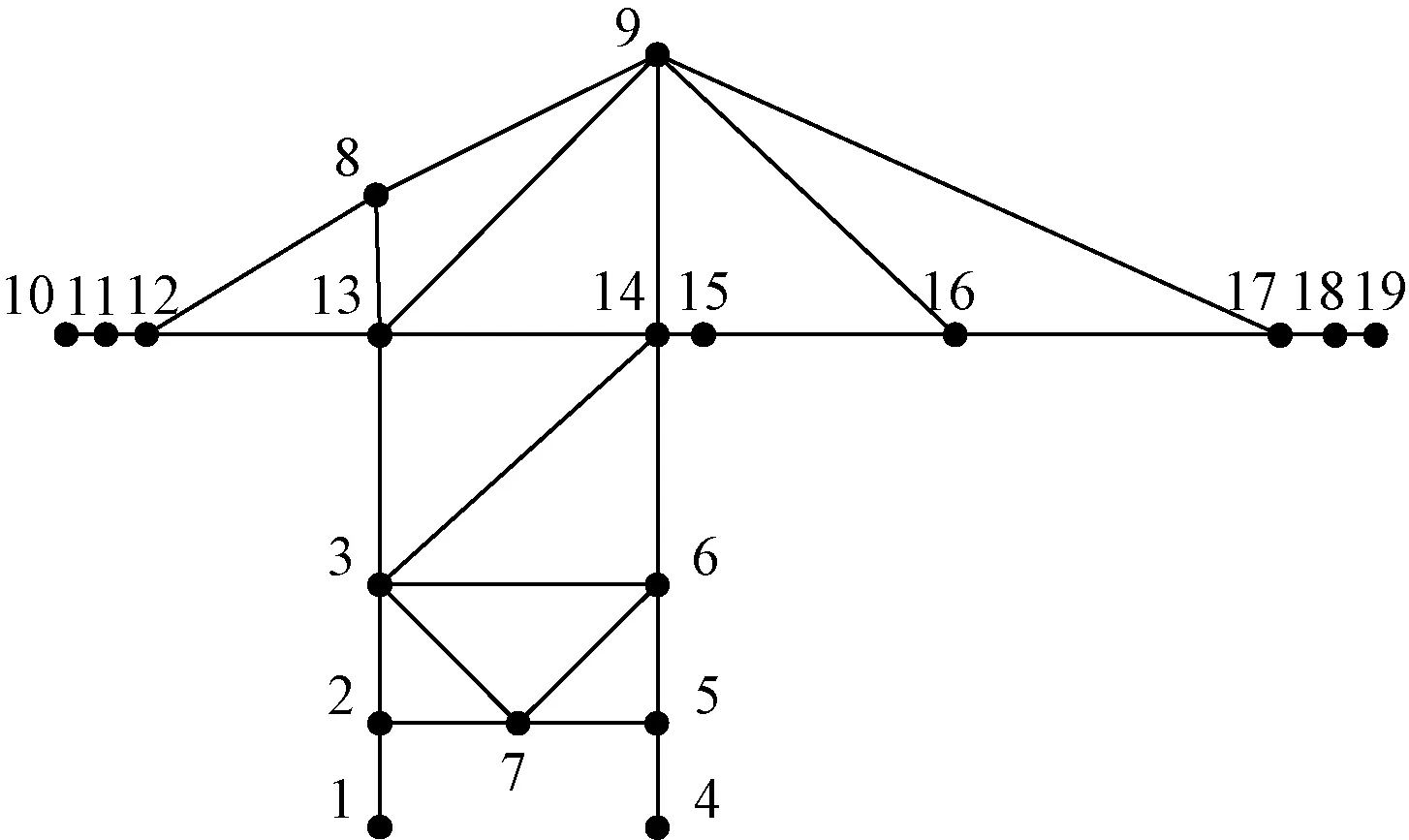
1～19为节点图3 岸桥点值描述Fig.3 Point value description of quayside container crane

2 岸桥结构分析方法

选取某型号的岸桥作为分析对象，其中大梁长度为144.132 m，基距为30.48 m。如图3所示，对整机结构进行点值描述，其中拉杆用杆单元构建，其他结构用梁单元构建，节点15为前大梁与后大梁连接的铰接位置。岸桥作为一种结构复杂的大型机械，结构中存在铰点、不同单元耦合作用下的节点、质量点和高度变化的偏摆吊重等特点，所以需了解如何使用向量式有限元对这些特点进行分析。

2.1 铰接节点

为了使岸桥的前大梁在非工作状态下能够抬起，前大梁与后大梁的连接方式为铰接。假设前大梁与后大梁通过一个铰接点连接，为了模拟出铰接的两单元的相对转动，需要对单元的内力计算公式进行修改。

以1-2梁单元为例，对于常见的刚接节点，单元两端的节点内力计算公式为[15]

(13)

以14-15单元为例，前大梁与后大梁通过铰接点15进行连接，由铰接结构的性质可得

(14)

式(14)中：m15-14和φ15-14分别为单元14-15中节点15的弯矩和转角。

将式(14)代入式(13)可得与铰接点连接的单元两端节点的内力计算公式为

(15)

在使用ANSYS软件设置铰接节点时需要设置多个相同位置的节点后根据铰接关系设置约束，过程较为复杂。使用向量式有限元分析只需判断节点的连接方式，选择对应的内力计算公式进行计算。

2.2 耦合单元节点

对于岸边集装箱起重机来说，起重机主体使用梁单元来构建，但结构中的拉杆不承受弯矩的作用，因此需要使用杆单元来描述。对于同时连接杆单元与梁单元的节点来说，如何正确描述不同单元间的耦合作用是需要解决的问题。

(16)

由梁单元的内力计算公式可得，梁单元16-17和17-18传递给节点17的内力为

(17)

至此得到了各个单元作用在节点17上的内力，由于内力都按照了坐标轴进行了分解，所以可得节点17受到的总内力为

(18)

在程序求解过程中对单元类型进行判断，将处于耦合单元位置的节点的内力计算公式进行替换。

2.3 结构自重与质量单元

在岸桥的ANSYS有限元模型中将部分结构用质量单元表示，在进行力学分析前要分析自重对结构的变形。在向量式有限元模型中可通过在每个节点上施加对应的重力来模拟结构自重的影响。假设节点i的质量为m′i，在此节点上施加的质量单元的质量为massi，则加入质量单元后此节点的质量mi=m′i+massi，取g为重力加速度，自重导致的垂直方向上的外力为

Pi=-mig

(19)

2.4 高度变化的偏摆吊重

(20)

(21)

图4 起升作用下吊重的位置变化Fig.4 Variation of lifting position under lifting action

3 动力学分析结果

使用ANSYS软件建立对应的有限元模型，如图5所示，使用单元为Beam188、Link180和Mass21，模型由159个节点表示。取小车质量10 t，吊重质量30 t，小车运行速度240 m/min，起升速度90 m/min，小车加速度为2 m/s2，连接吊重的钢丝绳绳长变化范围为30～4 m，吊重初始摆角为0.05 rad。

不考虑吊重的作用，将小车视为移动载荷进行分析，使用有限元软件与向量式有限元分析得到的大梁上各节点垂直方向上的位移如图6所示，节点编号所对应的位置如图3所示。可以看出，VFIFE与ANSYS软件求解得到的结果相比误差很小，并且在向量式有限元中整机结构只用了19个节点描述，用较少的节点便可得到精确结果。

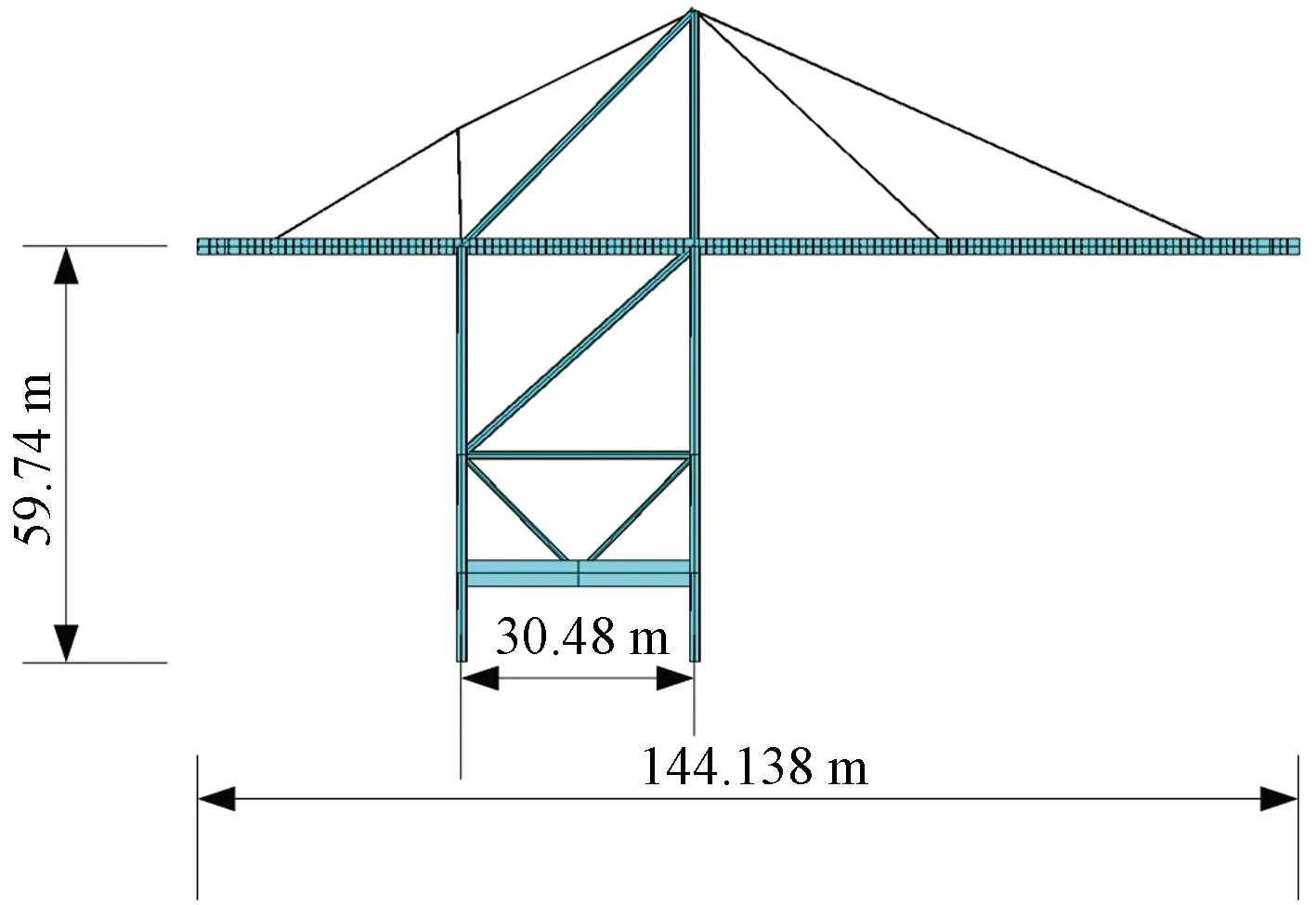
图5 岸桥的有限元模型Fig.5 Finite element model of quayside container crane

图6 移动载荷作用下的大梁位移Fig.6 Displacements of girder under moving load

前大梁与后大梁之间通过铰接点连接，在小车运行通过铰接点时，随着结构约束方式的变化，内力会发生突变。内力的突变也会导致位移的变化。由图6可知，将小车模拟为移动载荷时铰接点的作用不明显，因此将小车模拟为移动质量进行分析。

选取铰接点与前大梁最远端两个位置进行分析，其他相关参数保持一致，得到移动载荷与移动质量作用下的节点位移变化对比如图7所示。可以看出，在阻尼相同的情况下小车开始运动时移动质量作用下的结构振动更剧烈。与移动载荷相比，移动质量作用下的大梁在中间一段的曲线与其不同，曲线发生突变的时刻正是小车运行到铰接点位置的时刻。在考虑了小车惯性力作用的情况下，结构的位移变化在铰接点处发生了突变。

考虑小车的变速运动和吊重起升与偏摆，在小车运行时为了提高工作效率，吊重会经过起升-固定高度-下降的过程。得到大梁上各节点的挠度变化如图8所示，可知在小车的启动与制动阶段，结构会发生明显的振动。

图7 移动载荷与移动质量作用下的大梁位移对比Fig.7 Displacement comparison of girder under moving load and moving mass

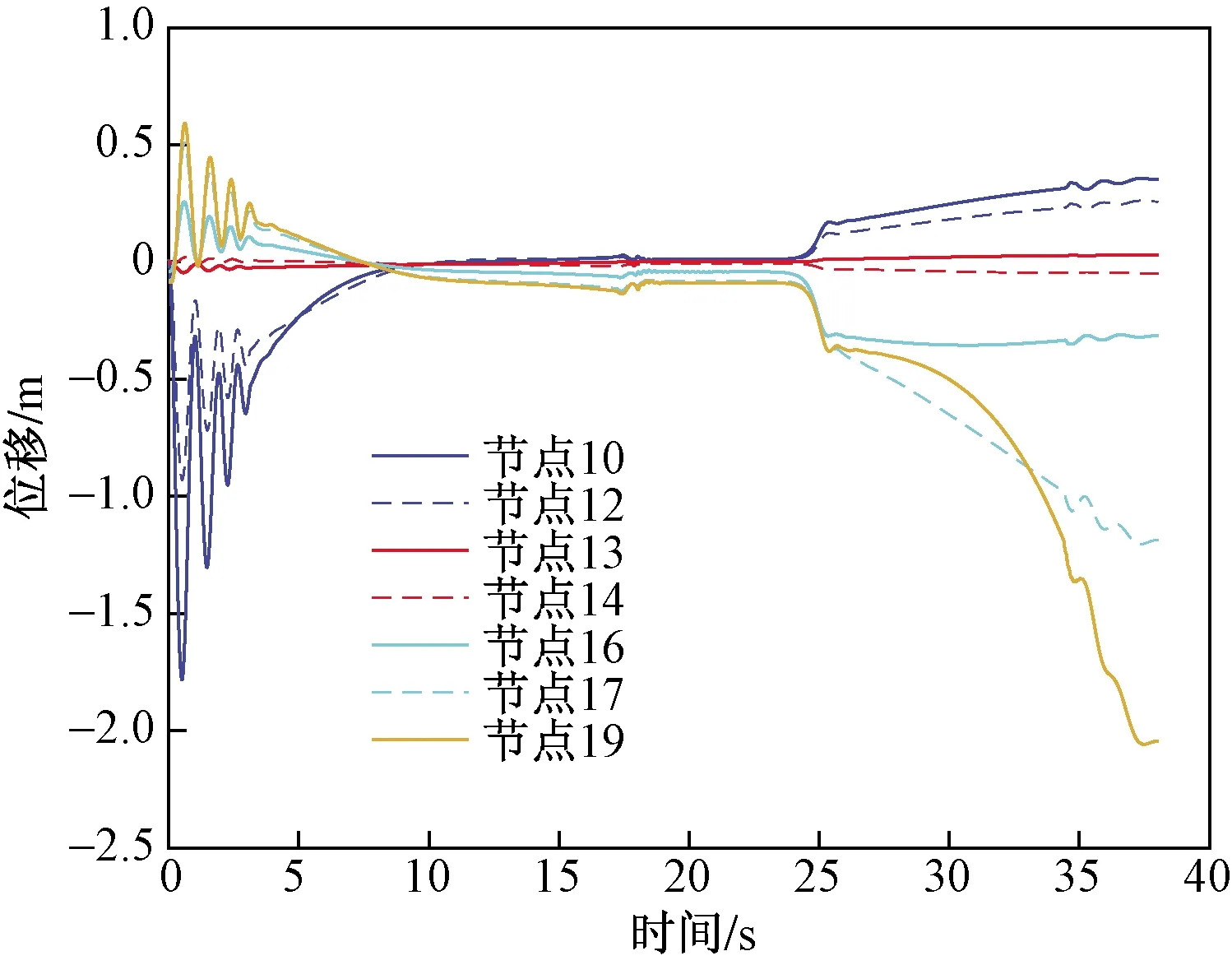
图8 移动吊重与小车作用下的大梁位移Fig.8 Displacement of girder under the action of moving lifting load and trolley

小车运行过程中吊重的相图如图9所示，可得随着高度升高，吊重的摆角减小。小车的启动与制动时的加速度会导致摆角发生较大幅度的变化，因此当重物的质量较大时，应适当减小小车的运行速度以起到防止摆角过大的作用。

图9 吊重的相图Fig.9 Phase diagram of lifting load

4 结论

基于向量式有限元杆单元与梁单元理论，进行了岸桥的动力学分析，得出如下结论。

(1)对岸边集装箱起重机的结构进行点值描述，并对结构中存在的铰接点、质量点、耦合单元和高度变化的偏摆吊重的处理方法进行说明。

(2)根据向量式有限元理论进行编程，使用ANSYS软件建立有限元模型，进行移动载荷作用下起重机动力学分析，说明向量式有限元只需选取结构的关键位置设置节点便可有较高的准确性。

(3)将小车模拟为移动质量进行分析，并与移动载荷作用下的结果进行对比，根据结果可得移动质量可以表现出小车运行至铰接点位置时的结构运动的突变。

(4)考虑小车运行中吊重的起升与偏摆，得到大梁上各点的挠度变化与吊重的相图，以此反映出小车运行对结构的影响。

将吊重简化为了约束点移动的变摆长单摆进行分析，从得到的结果可知在这种模拟方式下吊重会发生较大的偏摆。以后可以尝试模拟出更符合实际的小车与吊具结构，也可以添加防摇摆的措施以模拟更真实的情况。