带有仿生环形剪切腹板风机叶片抗弯强度

孟 杰， 张喜清， 孙大刚

(太原科技大学机械工程学院， 太原 030024)

风力发电是一种清洁型发电方式，已成为当今世界新能源的发展潮流，风力发电机的大型化和风电场的规模化是当今风电的发展趋势。随着风力发电机单机装机容量的增大，叶片趋于细长型。在风场气动力、弹性及惯性力耦合作用下，叶片更易出现颤振及扭曲，甚至疲劳断裂。因此提高风力机叶片的抗弯性能成为影响风力发电机向大型化发展的重要因素，也成为当下研究人员关注的热点问题。

一般采用腹板中空式结构，降低叶片重量，提高其强度与刚度[1]。设置剪切腹板可承受与叶片弯曲有关的剪应力，保证叶片稳定性[2]。李欢等[3]研究发现离心力载荷对叶片结构性能的影响大于气动力载荷；刘宇航等[4]基于复合材料铺层实现叶片气动弹性裁剪，采用节点位移法分析铺层结构对弯扭耦合叶片整体性能的影响；杨瑞等[5]研究发现缘条结构有助于减小叶片变形、改善黏结区应力分布以及改变叶片固有频率，其中对单腹板叶片改善较小，对双腹板叶片改善明显；周展鹏等[6]对翼型内部结构为单腹板和双腹板的风力机叶片进行了模态、应力和应变分析，结果表明：双腹板叶片的力学性能优于单腹板叶片；Choudhury等[7]提出一种改进型叶片，发现在整个展长内添加不同翼型轮廓的腹板，可以减小叶片气弹效应，提高输出扭矩；张立等[8]建立了一种非规则仿树叶脉络分布的腹板模型，研究发现仿生腹板更具柔性，吸收更多结构变形能，具有更好的抗共振性能，同时可节省1/2材料。

以上研究主要包括气弹载荷、离心力载荷、复合材料铺层对叶片结构性能的影响，及纵向单、双腹板和不同翼型腹板叶片的力学性能。但从仿生角度改良叶片结构的研究甚少，即使上文提到的仿树叶脉络腹板的非规则结构在制造中亦有难度。

自然界中的毛竹在强风环境中大角度弯曲不易折断，且其具有薄壁特征及悬臂结构的特点，与风力机叶片相似。所以借鉴毛竹规律性分布地竹节隔板支撑竹竿壳体的结构，提出一种新型的仿生环形剪切腹板叶片结构，通过建立叶片受力模型，进行数值仿真，研究其抗弯性能，为高强度叶片结构的设计与优化提供参考。

1 带有环形剪切腹板叶片的力学模型

在植物界中，毛竹属于细长型薄壳结构，其生长高度可达20 m以上[9]，长径比值在100以上，经过长期的自然进化已具有优良的抗风载能力。竹节的规律性分布使得竹竿径向形变更加均匀，避免出现局部应力过度集中，产生大变形，甚至断裂。另外，竹节属于实心隔板结构(图1)，在毛竹弯曲变形时可以有效支撑竹竿壳体，抑制进一步形变。因此，借鉴毛竹竹节的特点，在风力机叶片内部添加仿竹节结构的环形剪切腹板(图2)，以提高叶片的抗弯性能。

图1 竹节结构

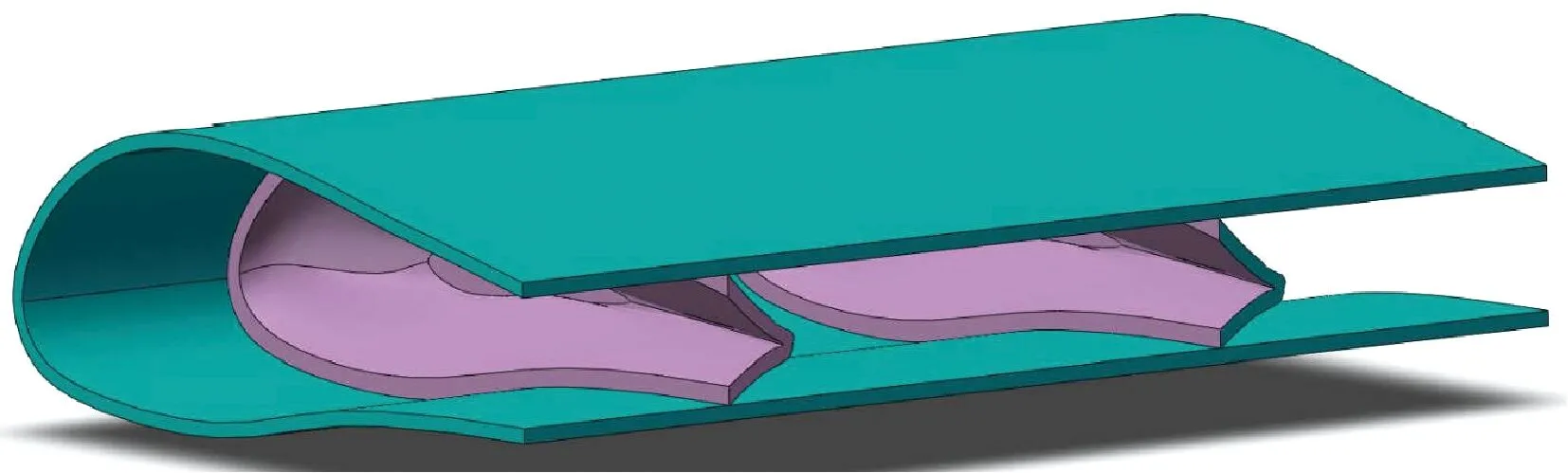
图2 带有环形剪切腹板的叶片结构

腹板设置在沿翼型截面方向，所以取翼型截面为研究对象，如图3所示。由定常气动理论可知叶片展长的气动力[10]为

(1)

式(1)中：ρ为来流空气密度；Cd为阻力系数；Cl为升力系数；S为叶片面积。当表示叶片展长某微段dx的气动升力Flx和气动阻力Fdx时，式(1)可变换为

(2)

式(2)中：Cdx为微段dx处的阻力系数；Clx为其升力系数。

叶片属于悬臂梁结构，在额定载荷下做匀速圆周运动，其受力均匀；而在启动风速和停机风速下，叶片承受的风载荷最大，极易发生断裂破坏。在风力机运行过程中，当风载荷与叶片重力方向相反时，叶片是最安全的[图3(a)]，当二者方向相同时，叶片发生断裂的可能性最大[图3(b)]。

α为攻角；vf为风速；气动力(风载荷)F分解为垂直的气动升力Fl和平行的气动阻力Fd；c为截面翼型弦长；G为叶片重力

如图4所示，由弯曲内力平衡方程[11]∑P=0与∑M=0可得叶根处的支反力为

b为叶片展长；P为叶根处支反力；M为叶根处支撑弯矩

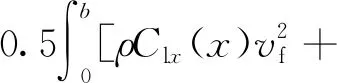
(3)

(4)

式中：Gx为叶展微段dx的重力，可表示为

(5)

式(5)中：ρ′为材料密度；Cx为截面翼型周长；h为周长Cx与弦长cx的比例系数。叶片任意截面x处剪力与弯矩分别为

(6)

(7)

将叶尖速比λ=ωR/vf和b=δR代入式(6)和(7)，可得

(8)

(9)

式中：ω为风轮旋转角速度；R为风轮半径；δ是展长与风轮半径的比例系数。

叶片截面上的最大正应力发生在距中性轴最远的点上，表示为

(10)

叶片材料的应力应变关系式[12]为

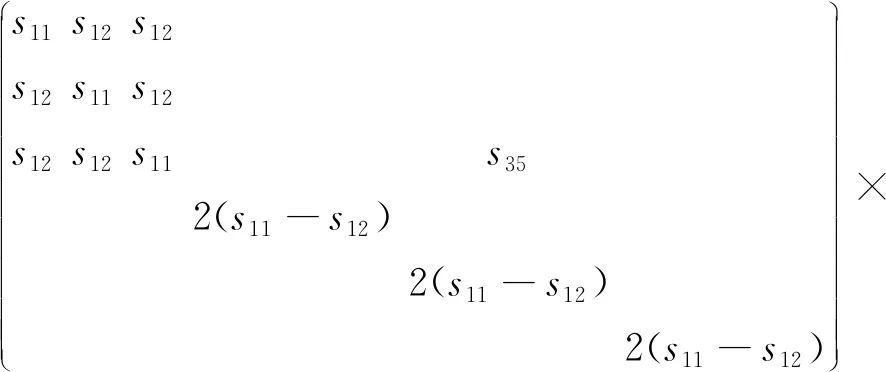
(11)

式(11)中：ε为正应变；γ为剪应变；σ为正应力；τ为剪应力；s为柔度系数。

(12)

(13)

式(13)中：u、v和w分别为环形剪切腹板处沿x、y和z方向的位移。

基于柔度系数与工程弹性常数的关系，将s12=-ν12/E、s11=1/E和s35=η13,3/G13[14]代入式(13)中，可得叶片在风载荷作用下距叶根x处截面的位移为

(14)

式(14)中：E为材料的弹性模量；G为材料的剪切模量；νij为泊松比；η13,3为第一类相互影响系数。

如图5所示，将翼型截面曲线分为内环上曲线ziu(y)、内环下曲线zid(y)、外环上曲线zou(y)及外环下曲线zod(y)，分别表示为

图5 环形剪切腹板示意图

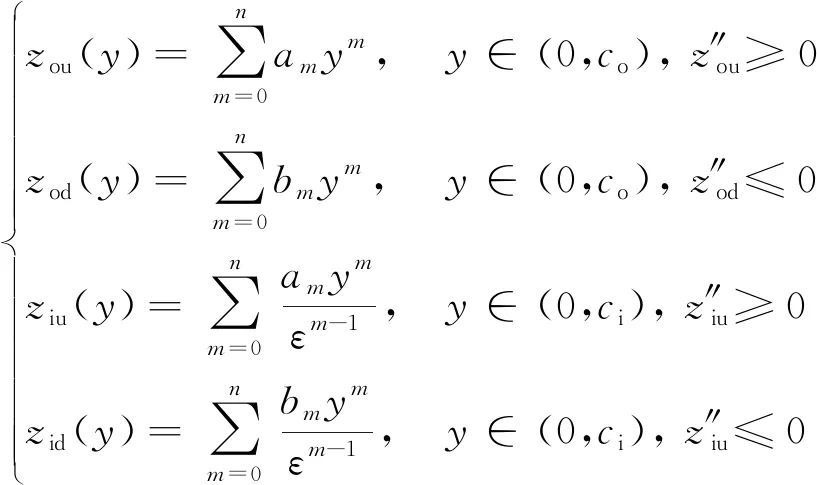
(15)

且满足在区间(0,ci)内，对于任意取值的y，满足zou(y)-ziu(y)>0且zod(y)-zid(y)<0。

式(15)中：am和bm分别为外环上曲线和下曲线多项式函数的各幂次项参数；ε为内环弦长ci与外环弦长co的比值。

外环及内环的截面惯性矩Ioy及Iiy可分别表示为

(16)

将式(15)代入式(16)，可得出环形剪切腹板处的惯性矩为

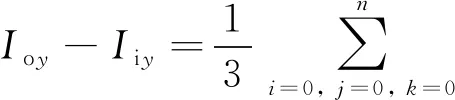
(17)

将式(9)和式(17)代入式(10)得

(18)

在风载荷作用下，距叶根x处叶片发生弯曲变形，叶片的转角为

(19)

由于叶片弯曲变形，翼型截面的相对厚度D减小，减小量可表示为

(20)

即

(21)

式(21)中：us为叶片弯曲形变拉伸部分沿x方向的位移;uc为叶片弯曲形变压缩部分沿x方向的位移。

式(21)表明，翼型截面厚度的减小量不仅与叶片材料及外载荷有关，与其惯性矩也有密切关系。在不同外载荷及材料条件下，可以通过调整环形剪切腹板的内外弦长比值，控制翼型截面厚度减小量。

2 仿真计算

选用750 kW风力机进行仿真实验，叶片外形采用NACA4412航空翼型，相关参数[15-16]如表1和表2所示。

表1 风力机叶片参数

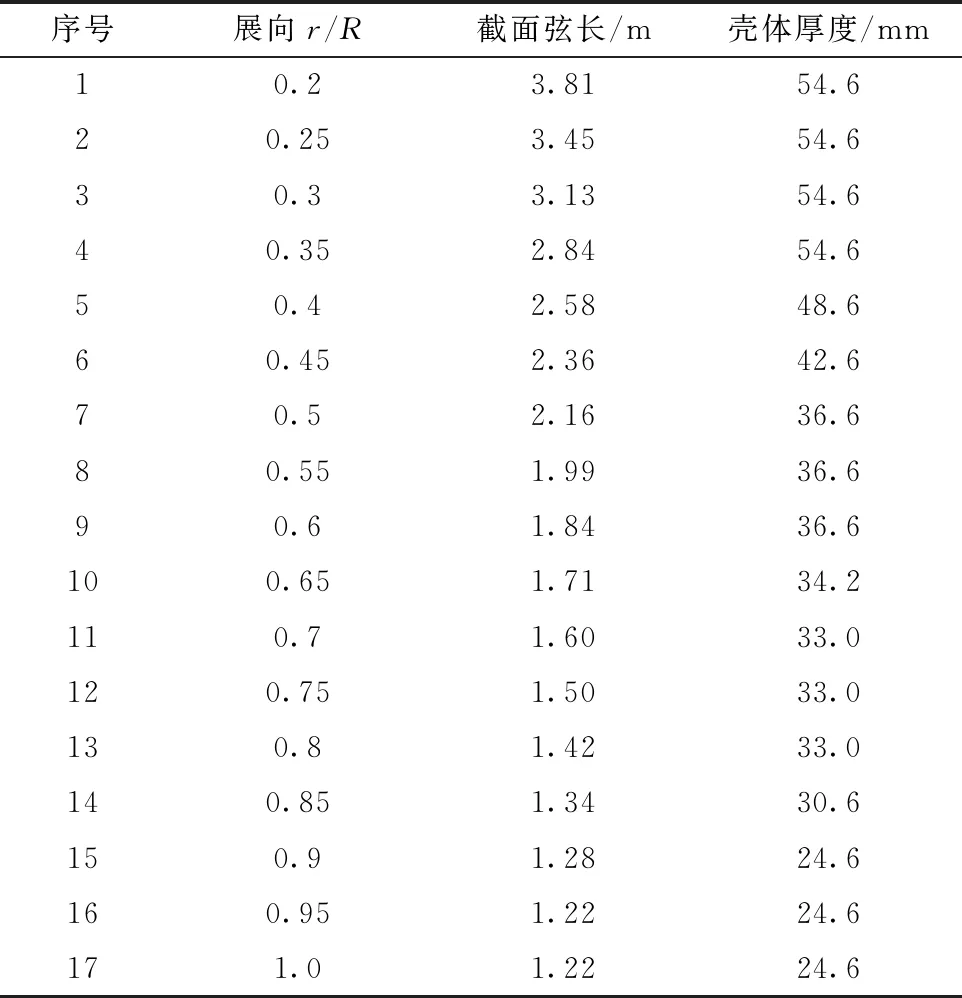
表2 叶片壳体厚度Fig.2 Blade shell thickness

采用xflr5软件对机翼NACA4412进行气动计算。雷诺数为0.5×106,攻角变化范围是0°～21°，增加小步是+0.5°。从xflr5数据库中得到升力和阻力系数随攻角变化的数据。最大升阻比为109.817，相应攻角是6.5°，升力系数是1.163。通过Origin Pro8软件获得升力系数Cl随攻角α的变化规律为

Cl=-4.76×10-3α2+1.42×10-1α+4.4×10-1

(22)

叶片弦长c随展长b的变化规律(叶片总长度24.2 m，翼型始于距叶根4.84 m处，即0.2b)为

c=-2.39×10-4x3+1.73×10-2x2-4.66×10-1x+5.69， 0.2b≤x≤b

(23)

翼型NACA4412最大相对厚度D=0.120 2c，所以最大相对厚度D随展长b的变化规律为

D=-2.87×10-5x3+2.08×10-3x2-5.60×10-2x+6.84×10-1， 0.2b≤x≤b

(24)

攻角α随展长b的变化规律为

α=2.64×10-4x4-1.96×10-2x3+5.57×10-1x2-7.69x+46.67， 0.2b≤x≤b

(25)

结合式(18)和式(22)，升力系数Cl随展长b的变化规律为

Cl=-3.33×10-10x8+4.93×10-8x7-3.23×10-6x6+1.23×10-4x5-3.52×10-3x4+8.59×10-2x3-1.56x2+17.71x-96.63, 0.2b≤x≤b

(26)

微段重力G可以表示为

G=-2.89×10-2x3+2.1x2-56.58x+689.91, 0.2b≤x≤b

(27)

翼型截面NACA4412上、下曲线表示为

zu=-4.71×10-10y6+1.56×10-7y5-2.01×10-5y4+1.3×10-3y3-4.71×10-2y2+9.65×10-1y+7.75×10-1

(28)

zd=4.60×10-10y6-1.52×10-7y5+1.95×10-5y4-1.23×10-3y3+3.93×10-2y2-5.41×10-1y-4.98×10-1

(29)

在不同截面处，式(28)和式(29)可以表达为

9.65×10-1y+7.75×10-1c

(30)

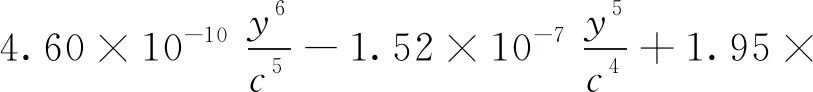
5.41×10-1y-4.98×10-1c

(31)

(32)

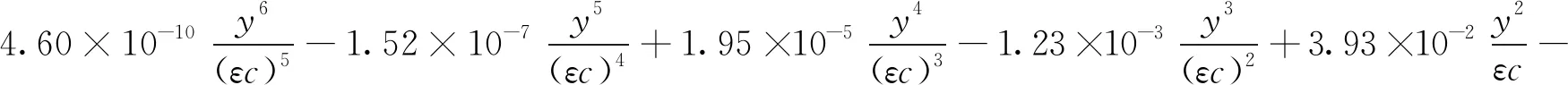
(33)

利用式(26)～式(33)可以推导出惯性矩Iy，最大正应力σmax和翼型相对厚度减小量ΔD。

3 结果与分析

利用MATLAB软件对在极限荷载作用下模拟安装了环形剪切腹板的风力机叶片进行分析。当ε=0时，腹板被视为实心腹板,当ε>0时，腹板被视为环形腹板。由式(17)看出，环形腹板截面与实心腹板截面不同，其惯性矩Iy也不同。从式(10)和式(20)看出，最大正应力σmax和翼型相对厚度减小量ΔD也不同。为了探究两种腹板惯性矩Iy，最大正应力σmax和翼型相对厚度减小量ΔD的不同，需要研究这些变量随叶片内外弦长比ε和展长x的变化规律。

图6所示为截面惯性矩Iy随叶片内外弦长比ε和展长x的变化规律。可以看出：ε越大，Iy越小。ε=0.1时的Iy分别为ε=0.4、ε=0.7和ε=0.9时的1.01倍、1.2倍和5.4倍。另外，4.84 m处的Iy远大于叶尖处，从表3可以看出，4.84 m处的Iy分别是14.84 m处和24.20 m处的18倍和117.6倍，Iy随展长增大逐渐变小。从式(17)看出：Iy值与展长呈非线性关系，因为叶片截面积与展长呈非线性关系，且截面积越大，这种关系越明显。

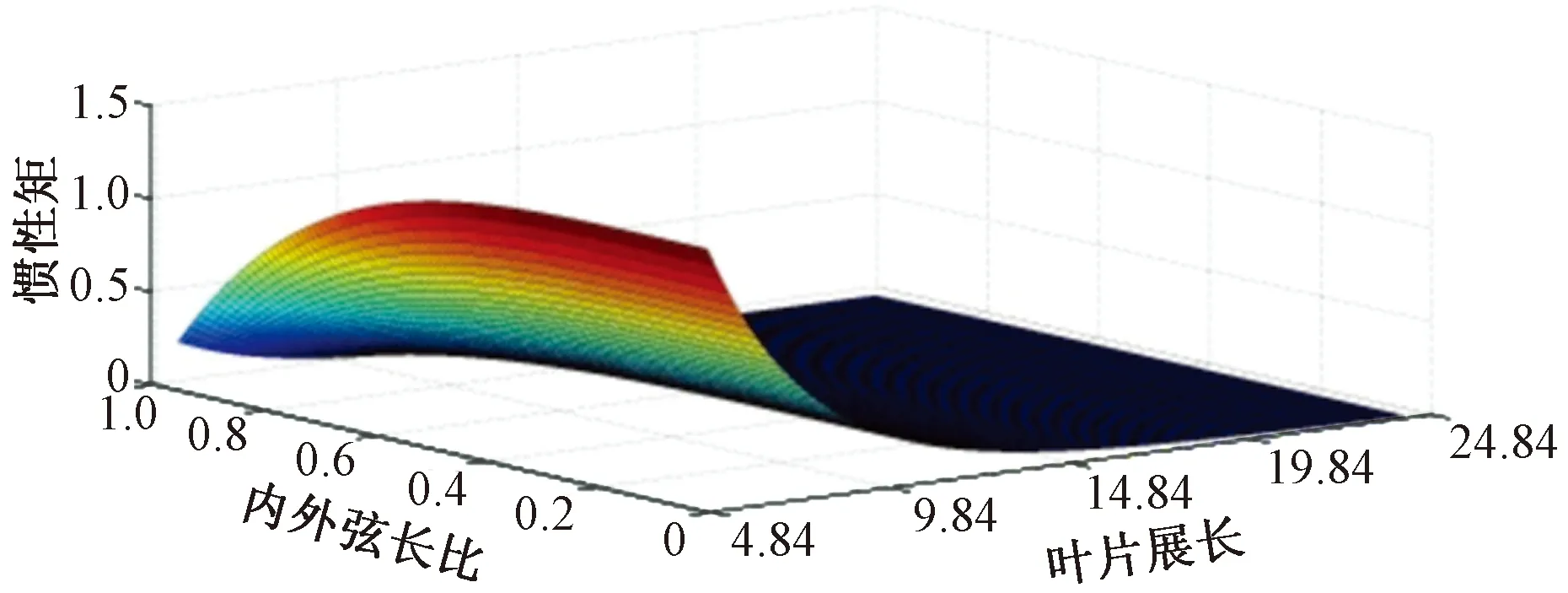
图6 惯性矩变化趋势

表3 沿展长方向，不同内外弦长比值时，惯性矩、最大正应力和减小量值

图7(a)所示为最大应力σmax随内外弦长比ε和展长x的变化规律。可以看出，ε值越大，σmax越大，ε=0.9时的σmax分别是ε=0.7、ε=0.4和ε=0.1时的4、5.3、5.4倍。从式(17)看出：Iy与ε呈非线性关系，所以σmax与ε亦呈非线性关系。另外，展长4.84 m处的σmax远大于叶尖处，这与实际情况符合。从表3可以看出，越接近叶根处，最大正应力越大；越接近叶尖处，最大正应力越小。4.84 m处的σmax分别是14.84 m和24.20 m处的6.6倍和163.8倍。σmax延展长逐渐减小。从式(7)和式(10)看出：Iy和M与展长均呈非线性关系，所以σmax与展长亦呈非线性关系。

图7(b)所示为最大应力σmax随内外弦长比ε和叶尖速比 (tip speed ratio，TSR)的变化规律，当TSR=8时，σmax远大于TSR=2时。σmax随叶尖速比增大而增大，两者之间呈非线性关系，因为Iy和M与叶尖速比均呈非线性关系，这种关系可以从式(9)和式(18)得出。

图7 最大正应力变化趋势

图8所示为翼型相对厚度减小量ΔD随内外弦长比ε和展长x的变化规律。可以看出，ε越大，ΔD越大，ε=0.9时的ΔD分别为ε=0.7、ε=0.4和ε=0.1时的4.5倍、5.3倍和5.4倍。从式(17)和式(19)看出Iy与ε呈非线性关系，所以ΔD与ε亦呈非线性关系。另外，在展长4.84 m处的ΔD远大于叶尖处。从图7和表3可以看出，4.84 m处的ΔD分别是14.84 m处和24.20 m处的6.7倍和163.8倍。ΔD沿展长逐渐减小，二者呈非线性关系，因为从式(19)和式(20)中看出Iy和M与展长均呈非线性关系。

从图7(a)、图8和表3可以看出，在叶片展长为4.84～14.84 m时，如果ε接近1，σmax和ΔD越大，并且越接近叶根处，两者越大，所以叶根部最容易断裂，此处最需要安装剪切腹板以减小最大应力值σmax和减小量ΔD。此外，值得注意的是，若ε为0～0.4，σmax则在1.95～1.99×107Pa范围内变化，ΔD则在0.001 3～0.001 5 m变化。也就是说：ε=0.4时，σmax和ΔD与ε=0时几乎相同，即内外弦长比ε选为0.4时的环形剪切腹板对提高叶片根部抗弯强度的作用与实心剪切腹板几乎相同。

4 结论

采用理论建模和数值模拟相结合的方法探究了风力机叶片抗弯性能随仿生环形剪切腹板形状参数的变化规律，分析了翼型截面惯性矩Iy、最大应力σmax、翼型相对厚度减小量ΔD随内外弦长比ε和展长x的变化趋势，得到如下结论。

(1)翼型截面惯性矩Iy随内外弦长比ε和展长x的增加而减小，且皆呈非线性关系；最大应力σmax随内外弦长比ε和叶尖速比TSR的增加而增大，而随展长x增加而减小，且均呈非线性关系；翼型相对厚度减小量ΔD随内外弦长比ε增加而增大，随展长x增加而减小，亦皆呈非线性关系。

(2)当内外弦长比值ε=0～0.4，最大应力σmax值和翼型相对厚度减小量ΔD的变化较小。即内外弦长比值ε=0.4时，环形剪切腹板可以显著提高叶片抗弯强度，与实心剪切腹板相比无明显差别。又由于环形剪切腹板呈中空形状，与实心腹板相比其质量明显减小，因此环形剪切腹板在提高叶片抗弯强度的同时有助于实现叶片的轻量化。