一种自然通风防辐射罩的设计与研究
孙中琳, 刘清惓*, 杨 杰, 张婷婷
(1.南京信息工程大学电子与信息工程学院, 南京 210000; 2.江苏省气象探测中心, 南京 210000;3.江苏省气象探测与信息处理重点实验室, 南京 210000)
在全球变暖的背景下,气温变化成为人们关注的重点,相关问题也被世界各地的政府组织和公众广泛讨论。据研究,喜马拉雅地区的冰川范围持续减少,对未来能否可持续发展带来关键挑战[1];水温升高1~2 ℃可能会加速许多热带水域生物的死亡[2];植物生长期将会发生变化,从而导致温室效应恶性循环[3]。目前全球平均气温较20世纪50年代已经上升了约1 ℃[4]。预测表明,到21世纪末,如果不进行减排减碳,还有可能上升2.5~4 ℃[5]。由此可见,气温变化不管是对于地球生态或人类生活来说都非常重要,气温监测的准确度更是研究气候变化的重要因素。
气温的监测主要是由温度传感器进行采集,但由于太阳直接辐射、散射辐射、下垫面反射辐射等多重辐射的影响,一般气象站通常会利用百叶箱或者防辐射罩等设备来保护传感器,但也同时会造成通风性差、温度变化不同步的问题。任芝花等[6]用了5个月的时间对比了两种不同材质的百叶箱对于大气温湿度的变化反应,玻璃钢百叶箱更胜一筹。徐伟等[7]针对上海枫泾区域2012年自动气象站的数据进行分析,发现轻型百叶箱对于大气温度的变化比玻璃钢百叶箱更敏感。袁超等[8]通过对比防辐射罩和百叶箱的温度样本观测数据,发现防辐射罩的通风比大于百叶箱。阳艳红等[9]在郑州国家基准气象观测站做了不同防辐射罩的对比实验,找出了其在材料上和结构上的差异。他们认为在设计防辐射罩时,首先应考虑通风性是否良好,其次再考虑材料防辐射特性。Richardson等[10]提出了一种具有抛物线截面的Gill防辐射罩优化结构,一定程度上提升了通风量,但未量化新结构的辐射误差。Erell等[11]针对不同形状和材料的防辐射罩进行了研究,发现其平均辐射误差在1 ℃量级。Zachary等[12]设计了一种盾牌结构防辐射罩,其成本远低于市场价,但平均辐射误差为0.99 ℃。Christoph等[13]提出了一种强制通风防辐射罩,其温度误差约为0.2 ℃,难以满足高精度观测的要求。
与百叶箱相比,防辐射罩体积小、成本低,且结构简易、安装携带方便[14],所以应用日益广泛。它的通风结构设计可以有效提高罩内传感器附近的气流速度,同时还可以减少来自个各个方向的辐射,保护内部传感器免受雨、雪、风沙等恶劣天气的破坏。但防辐射罩的结构样式繁多,因此,有必要对其进行研究,以提高工作性能,减小辐射误差,提高测温精确度。
1 防辐射罩流体动力学分析
1.1 防辐射罩物理模型
本文中设计的多导管式球形防辐射罩模型如图1所示,包括1个球形导流罩及均匀分布在导流罩外壁上的8根导流管道。导流罩呈球形,直径40 mm,厚度1.5 mm,此结构可有效引导自然风在罩内流通,减少各个角度的太阳辐射及下垫面反射辐射。导流管道呈圆台状,内径为7 mm,外径为12 mm,长度为30 mm,厚度为1.5 mm。测温时,温度传感器可置于导流罩截面的中心位置。
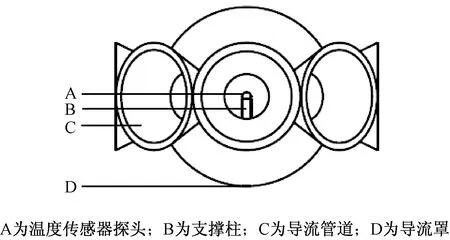
图1 模型示意图
1.2 多物理场仿真分析
地表温度传感器的测量误差主要包括传感器标定误差、电路误差和辐射误差。相对而言,辐射误差引起的温度误差比其他两个因素影响更为显著,尤其是太阳辐射误差[15]。为了与后续实验进行比对,并且在实际应用场景中,固定气象站的海拔、防辐射罩表面涂层反射率等因素几乎不变,对辐射误差影响较小,因此主要围绕太阳辐射强度、风速及太阳高度角三个因素与辐射误差之间的关系进行研究。
通过网格划分软件ICEM对防辐射罩模型不同计算区域进行不同的网格大小划分,保证了网格质量及仿真的收敛性和精度。当网格数量达到一百四十万时,网格质量良好。随后采用计算流体动力学(computational fluid dynamics, CFD)方法建立防辐射罩的流体动力学模型,如图2所示。空气入口设为速度入口,空气出口设为压力出口,同时开启太阳辐射模型,用来模拟真实条件下的太阳辐射强度及太阳高度角。
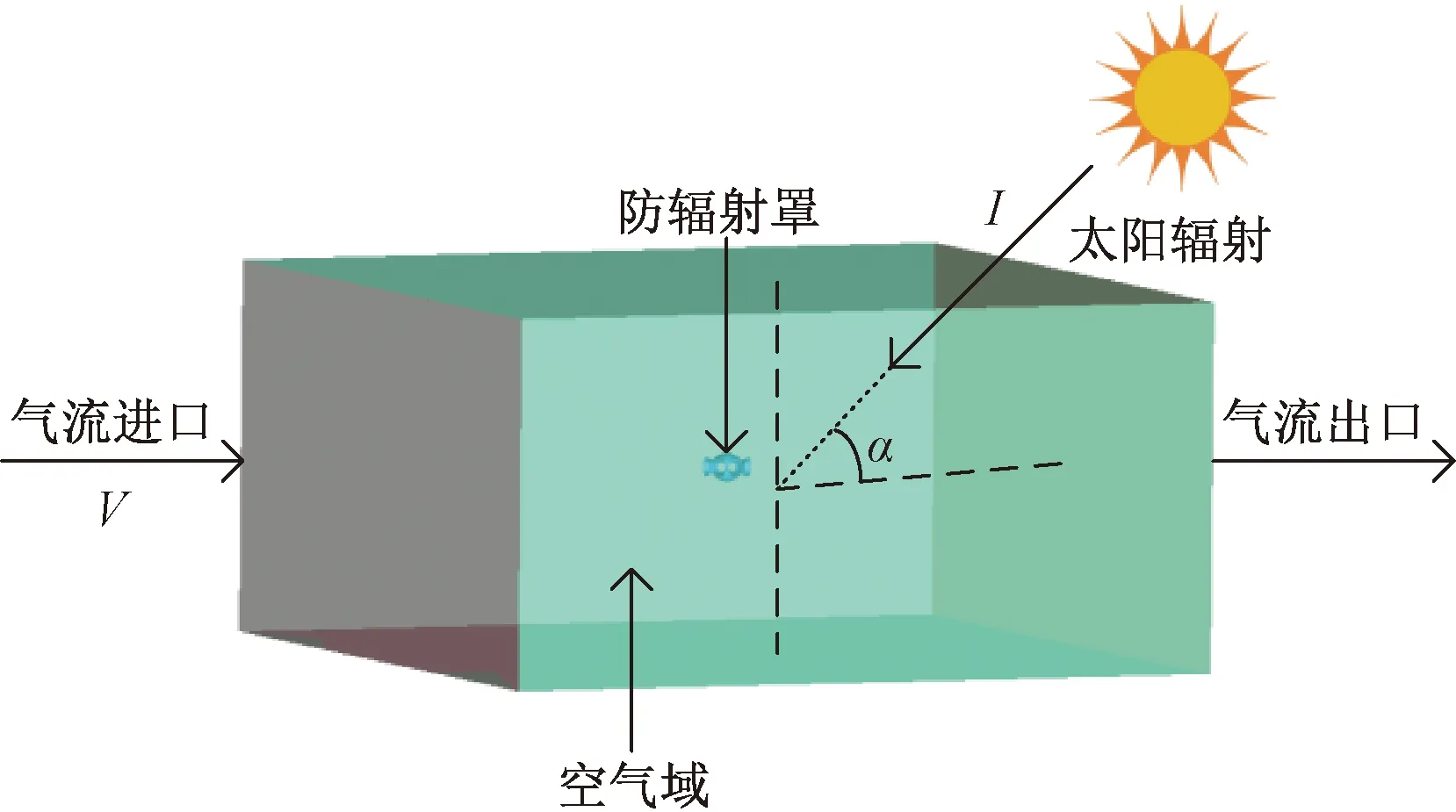
图2 仿真模型原理
设风速为V,太阳辐射强度为I,太阳高度角为α,辐射误差为ΔT。当V=4 m/s、α=45°、I=1 000 W/m2时,模拟结果如图3所示,防辐射罩中心的ΔT=0.059 ℃、V=3.003 m/s。由此可得,该防辐射罩具有良好的防辐射效果和通风性。
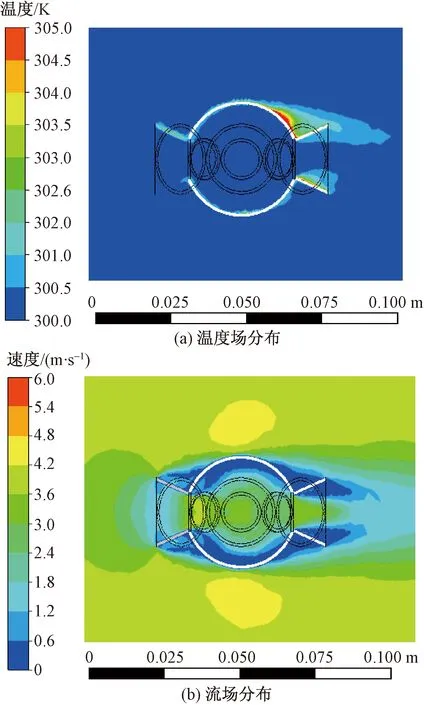
图3 防辐射罩内部温度场及流场分布
1.3 不同环境因素对辐射误差的影响
通过CFD方法分别对不同条件下的防辐射罩模型进行仿真,如图4所示,其中I、V、α范围分别设置为200~1 600 W/m2、1~16 m/s 、0°~90°。太阳辐射误差ΔT与I呈正相关,I越大,ΔT越大;与V呈负相关,V越大,ΔT越小;与α呈正相关,α越大,ΔT越大。

图4 不同条件下的辐射误差仿真结果
2 SVM算法设计
2.1 支持向量机回归算法
大气科学研究不仅需要对气候气象等要素进行监测,更需要对气候进行准确的预测。孙靖等[16]利用时间序列负荷预测法对空调负荷进行预测,发现此模型更适用于规律性较强的样本。李松等[17]研究表明神经网络预测法需要大量的样本进行训练,否则预测误差极有可能偏大。而支持向量机(support vector machine, SVM)模型更适用于样本少、波动大等问题[18],预测性能较好。
支持向量机回归算法就是找出输入样本数据和输出样本数据之间的映射关系,然后再利用这样的映射关系对其他样本数据进行预测。
回归问题的数据样本可表示为
T={(xi,yi),i=1,2,…,N}
(1)
式(1)中:N为训练样本数;xi为输入向量;yi为输出向量[19]。
SVM模型的建立包含样本集的建立、数据的归一化处理和训练集的选取训练等部分,其模型框架流程如图5所示,整个过程中的关键部分在于训练样本数据的构造、SVM模型及相关参数选取等。根据本文需求分析,所设输入为太阳辐射强度、太阳高度角和风速,输出为辐射误差。
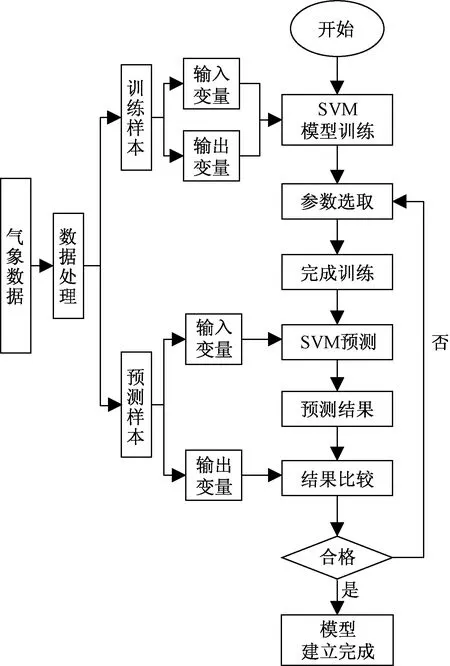
图5 SVM模型流程图
2.2 预测结果分析
选用LIBSVM工具箱,该工具箱内拥有很多默认选项供使用者直接设置,无需过多调节,并且具有运行速度快、运用灵活等特点,便于对数据做分类或回归[20]。
将SVM预测的结果与仿真结果进行比较,如图6所示,仿真值与预测值基本接近。为了便于结果分析,将仿真值与预测值相减得出绝对误差,如图7所示。误差值均介于-0.006~0.004 ℃,由此可见,算法预测精度较为准确。
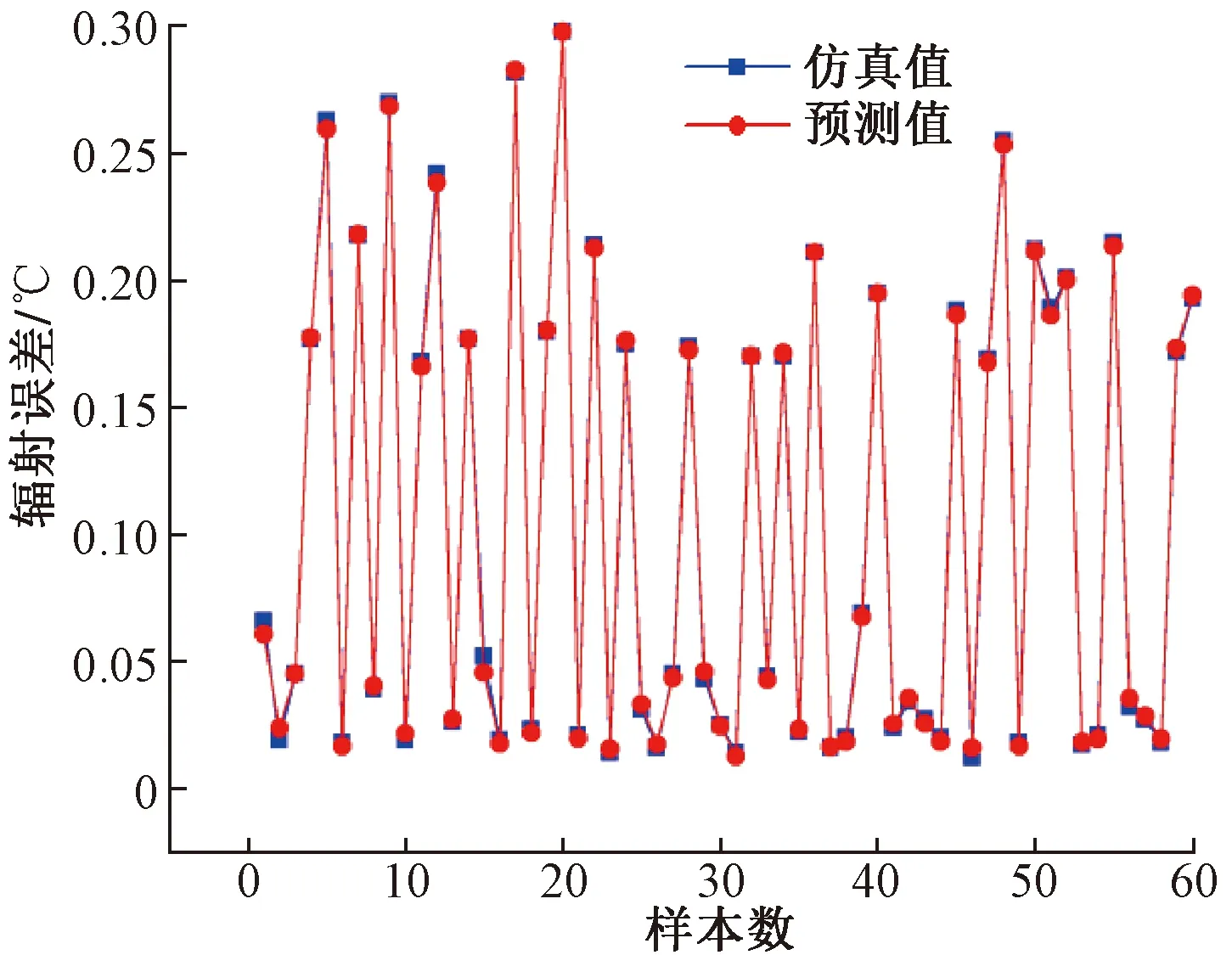
图6 仿真值与预测值对比

图7 仿真值与预测值的绝对误差
3 实验测试与分析
3.1 实验平台的搭建
为了验证防辐射罩的辐射屏蔽效果及算法预测精度,在中国气象局气象探测中心(南京)观测基地(32.12 °N,118.42 °E,海拔22 m)搭建了外场辐射误差测试平台,进行了为期4 d的大气温度观测比对实验。在实验过程中,以076B型强制通风防辐射罩的气温观测值作为温度参考,其产品手册上给出的误差值小于0.03 ℃。辐射误差测试平台如图8所示。
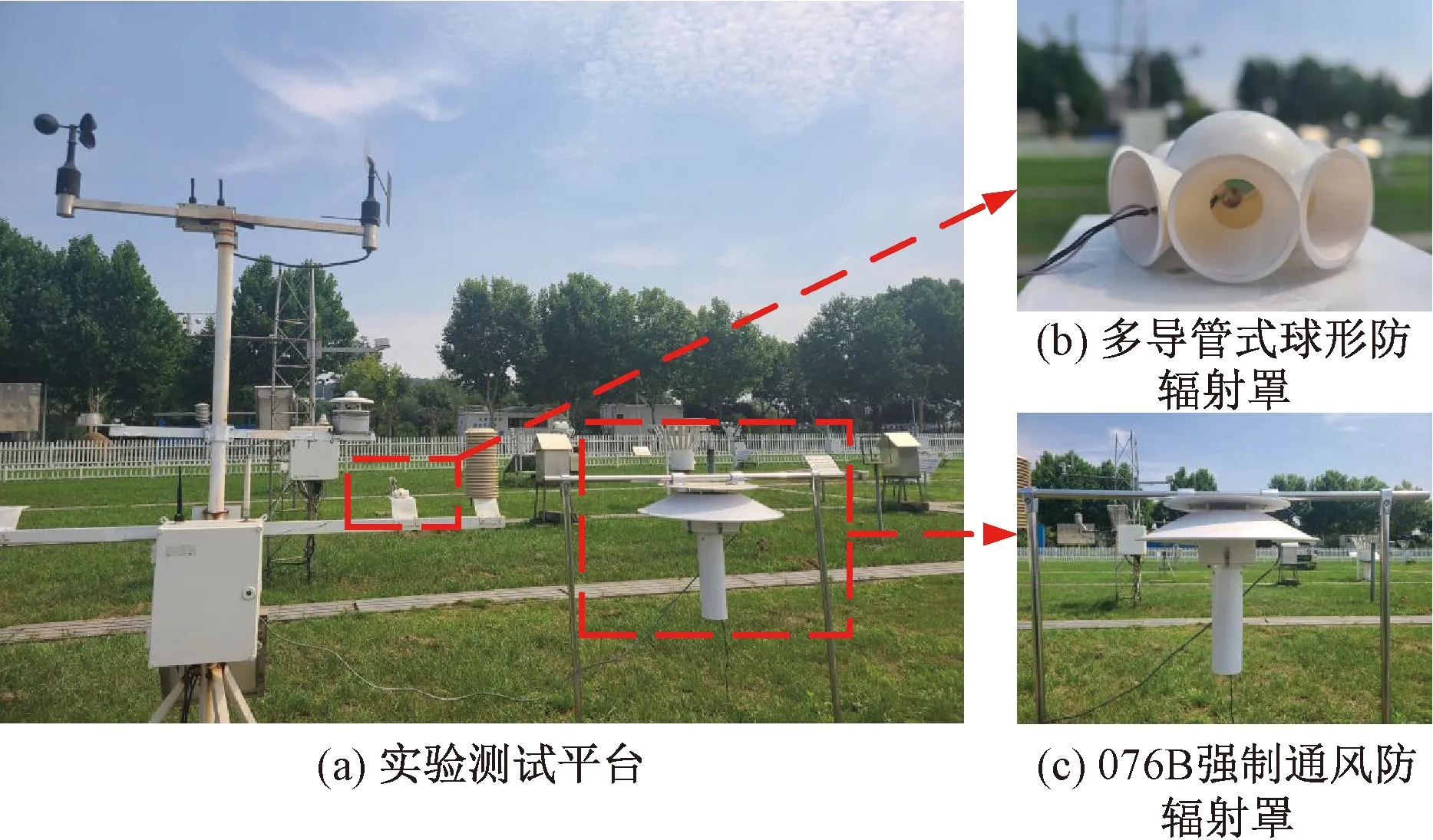
图8 实验装置图
3.2 实验结果分析
实验测得太阳辐射强度和风速结果如图9所示。将强制通风防辐射罩测得的温度与本设计测得的温度作差,得到辐射误差结果如图10所示,经计算得出本设计的平均辐射误差为0.081 ℃。因此,本文提出的多导管式球形防辐射罩具有较好的防辐射效果,可以有效提高测温精度。
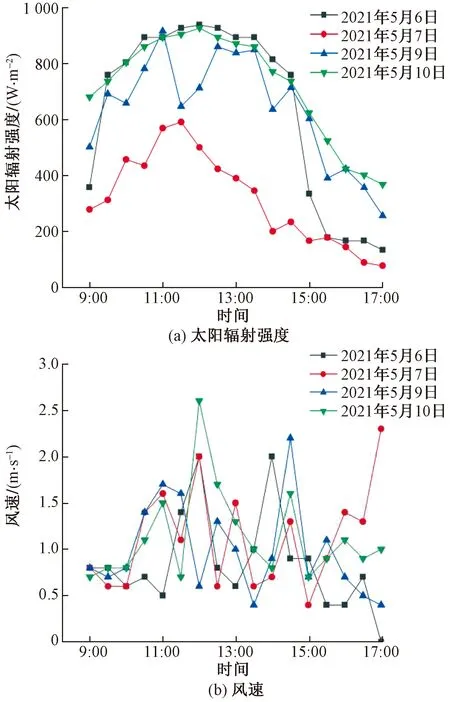
图9 不同时间下风速和太阳辐射强度的观测结果

图10 不同时间下的辐射误差
为了验证算法的预测精度,将实验测得的辐射误差结果和由预测模型提供的辐射误差结果进行比较,如图11所示。可知,算法预测结果与实验值相差较小。经计算得,实验给出的平均辐射误差和算法预测得出的平均辐射误差分别为0.081 ℃和0.047 ℃。由均方根误差(root mean squared error,RMSE)和平均绝对误差(mean absolute error,MAE),两个辐射误差之间的RMSE为0.054 ℃、MAE为0.039 ℃。RMSE、MAE的计算公式为

图11 不同时间下实验值和预测值的比较
(2)
(3)
式中:Epre为算法预测误差;Eexp为实验辐射误差;n为抽样总数。
由此可得,本文中设计具有较好的防辐射效果,且算法预测精度较高,对未来气象预报精度、气候趋势预测、气象灾害预警等相关科学研究有一定作用。
4 结论与展望
设计了一种多导管式球形防辐射罩。首先对防辐射罩外形结构进行设计;然后利用CFD方法量化太阳辐射强度、风速、太阳高度角等不同环境参数下传感器的辐射误差;接着,采用SVM算法训练出针对多变量变化的误差预测模型;最后,利用外场辐射误差实验平台对其辐射屏蔽效果及算法预测精度进行验证。由此可以得出以下结论。
(1) 本文提出的多导管式球形防辐射罩可将辐射误差精度降低至0.05 ℃量级,辐射屏蔽效果较好。
(2) 辐射误差的实验结果与预测结果的差值的均方根误差为0.054 ℃、平均绝对误差为0.039 ℃。表明算法预测值与实测值之间较为符合,预测模型准确性高,对未来气象相关科学研究有一定价值。

