考虑蓄水期弃水风险的水库长期发电调度方法
曹 瑞,程春田,申建建,蒋 燕,张聪通
(1.大连理工大学,辽宁 大连 116024;2.云南电力调度控制中心,云南 昆明 650000)
1 研究背景
我国西南水电经过十多年的大规模开发与集中并网实现了前所未有的发展,但与此同时也出现了巨大的弃水压力[1-2]。云南、四川两个水电规模最大的省份在过去5年产生了超千亿kW·h 弃水,相当于三峡年发电量规模,如何缓解弃水问题,对于充分利用水电等清洁能源、实现未来碳中和目标具有重要现实意义[3]。一方面,西南流域来水集中,全年超过50%水量分布在主汛期3 个月左右,水库调节库容不足再加之汛期复杂电网输电通道阻塞,可能导致部分弃水确实无法避免;另一方面,西南干流梯级通常有一座或者多座控制性水库,例如澜沧江的小湾与糯扎渡、乌江的洪家渡与构皮滩等,这些控制性水库的不合理调度决策也可能会引发较大的弃水风险。更具体来说,大型水库的长期调度与控制计算通常采用月或旬尺度的平均径流作为输入条件,但实际的日间以及日内水库入流一般是不均匀的,尤其是汛期遭遇洪水时,来水的时序波动更为明显,这就可能导致以平均径流为基础确定的中长期调度控制决策与实际存在较大差异[4],从而带来较大的弃水风险。如何描述这种弃水风险以制定合理的长期调度决策方案,是减少不合理发电调度弃水、促进西南水电消纳的关键问题之一。
近年来,已有大量研究工作开始关注水库调度弃水风险问题,时间尺度多为中短期,大致包括以下几个方面:(1)考虑径流预报的不确定性或误差分布,分析未来短时间内的调度弃水风险,作为实时水位控制或预泄调度的决策依据[5-6];(2)根据历史实际数据或未来可能情景,确定弃水风险不确定因素的概率分布,在调度应用中,基于概率分析结果制定调度规则或水位控制策略[7-8];(3)构建弃水风险指标,以评估特定运行状态或约束条件下的弃水风险,并将风险指标融入调度决策模型以实现弃水风险的有效管理[9-10]。另外,部分学者开始关注长期调度决策考虑弃水风险的实践意义[11-13]。例如Turgeon 等[12]提出一种水库最优运行水位确定方法,得到的最优水位轨迹能够适应年内不同时段弃水风险的变化;徐刚等[13]量化了水库入流不均匀性给长期调度带来的可能弃水,并在优化模型中考虑了经验频率下的弃水风险。实践证明,考虑水库中短期弃水风险可以有效提高长期调度方案的适用性,但常用的弃水概率方法不利于准确评价弃水损失,限制了其实际应用。
本文从实用性角度出发,结合控制性水库蓄水调度方式,提出一种蓄水期弃水风险定量评价方法,并以此为基础构建考虑蓄水期弃水风险的水库长期发电调度模型。首先,结合风险最小蓄水规则,以不蓄弃水流量为风险指标,通过历史日尺度径流资料统计蓄水期各月可能的弃水风险。其次,基于Copula 函数构建月均入流与弃水风险的联合分布和条件概率分布,定量分析月平均入流为特定值时的弃水风险并确定出风险置信区间。最后,将弃水风险以弃电损失的形式融入到优化模型目标函数中,以获得更符合实际的长期调度方案。所提方法的可靠性和有效性通过澜沧江流域小湾水库的调度模拟分析进行验证。
2 蓄水期弃水风险分析
本文以发电为主的年调节能力及以上的流域控制性水库为研究对象,为充分发挥“蓄丰补枯”调节作用,各时期的主要运行原则是:(1)汛前枯期:高效利用水库蓄能,合理控制水位消落,做好蓄水准备;(2)汛期:最大化水能资源利用,在充分蓄水前提下多发电、减少流域弃水;(3)汛后枯期:在满足综合利用需求情况下,维持高水位运行,提高水能利用率。流域控制性水库调度弃水风险通常集中在汛期蓄水阶段,在此期间水库来水量大且具有较强的波动性,加之库水位不断上升,运行中极易产生弃水。因此,在制定长期调度方案时非常有必要考虑蓄水期的弃水风险。
2.1 弃水风险评价指标考虑以月为尺度的长期调度在蓄水期因月内径流分布不均面临的弃水风险,根据历史日径流资料逐年计算蓄水期各月的可能弃水,并将月末水位作为日调度的目标蓄水位。在实践中,一般建议蓄水期库水位随时间推移逐步上升[14],则蓄水期各月目标水位应满足:

式中:t 为月尺度时段编号, t=1,2,…,T,其中T 表示调度周期时段数;Zt为t 时段末库水位,m;Ω 为蓄水期时段集合。
月内日尺度蓄水调度可概化为两阶段蓄水问题,依据两阶段蓄水规则运行[15],如图1 所示。图中横坐标表示当前可用水量;纵坐标表示下泄流量;Qmax表示不产生弃水所允许的最大发电流量;Rmin表示生态、通航、供水等所需的最小下泄流量;OA 段表示极端缺水情况,无法满足最小流量需求;ABD 段为弃水风险最小规则,表示当前时段尽可能多发电,直至发电流量超过Qmax才被动蓄水以减少余留期弃水风险;ACD 段为蓄水效益最大规则,要求尽可能减少下泄流量,直至蓄至目标水位;DE 段为超过目标蓄水位,将产生弃水;k 表示余留拦蓄库容;阴影部分表示风险对冲规则区,一般为单调非递减的线性或非线性形式,用于指导不确定性条件下的蓄水调度决策,以平衡运行效益和风险。
在蓄水期任一时段t 内,应用图1 蓄水规则进行日调度,当前时段可用水量为:
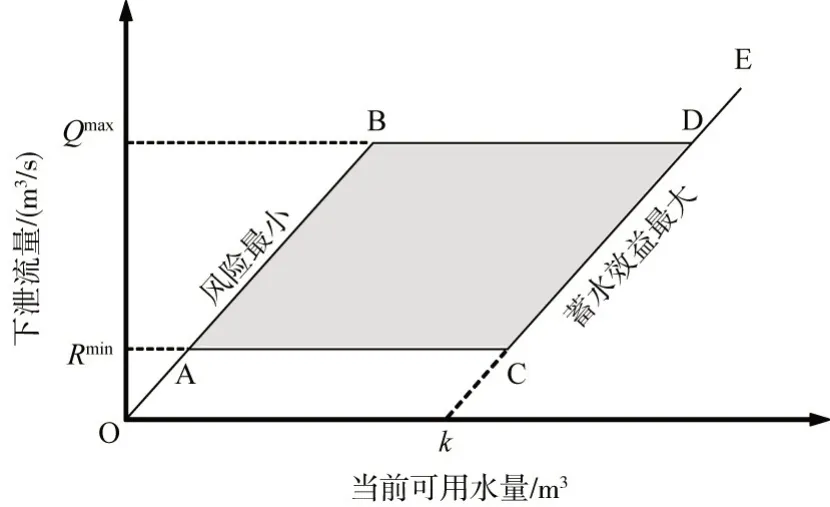
图1 两阶段蓄水规则示意

式中:d 为日尺度时段编号,d=1,2,…,Dt,其中Dt表示时段t 包含的天数;为d日初水库可调蓄水量,m3;为t 时段d日入库流量,m3/s;Δd 为一天的秒数。
由于蓄水期来水较多,可认为最小下泄流量需求总可以满足,则式(1)总能成立,因此图1 中横坐标可转换为即可用水量等于天然来水量。假定月内最大发电流量不变,在水库不蓄水情况下(k=0),根据图1 中风险最小蓄水规则(ABDE)能够得到t 时段不蓄弃水量为:

其中:
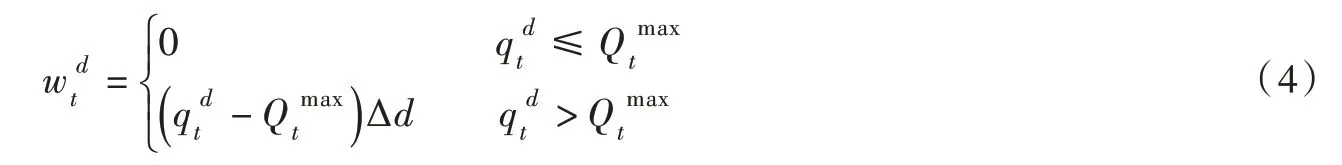
式中:Qtmax为t 时段最大发电流量限制,m3/s;为t 时段d日不产生弃水所需拦蓄的水量,m3。
以月为尺度计算不蓄水情况下时段t 的最小弃水量为:

式中: qt为t 时段水库平均入库流量,
Wt代表考虑月内径流波动后不蓄水情况下的最小弃水量估计,其与W ′t间的关系有三种情况:情况1。∀d 满足则Wt=W ′t=0 ;情况2。∀d 满足根据式(5)得到情况3。∃d 使且∃d 使根据式(4)和(5)可得出Wt>W ′t。
可以看出,当水库月均入流很小或者很大时,月内径流波动对弃水计算影响较小,可忽略不计。图2 给出了情况3 水库月均入流与不蓄弃水间的关系,可以看出虽然月均入流远小于最大发电流量,但由于天然径流的波动性,短时间尺度运行仍存在较大弃水风险。

图2 水库月均入流与不蓄弃水间的关系
依据式(3)可计算出水库蓄水期各月的不蓄弃水量,则月内日尺度蓄水方式取决于时段t 的拦蓄库容大小:

式中:Vt为水库t 时段末的可调库容,m3。
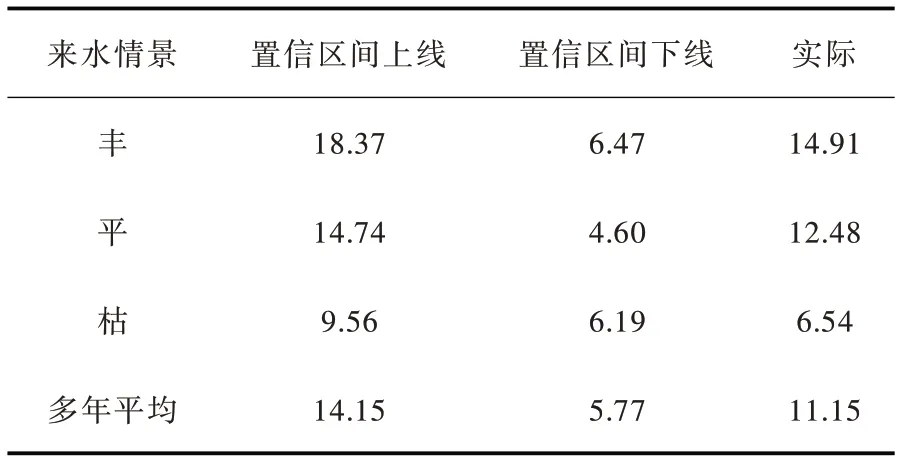
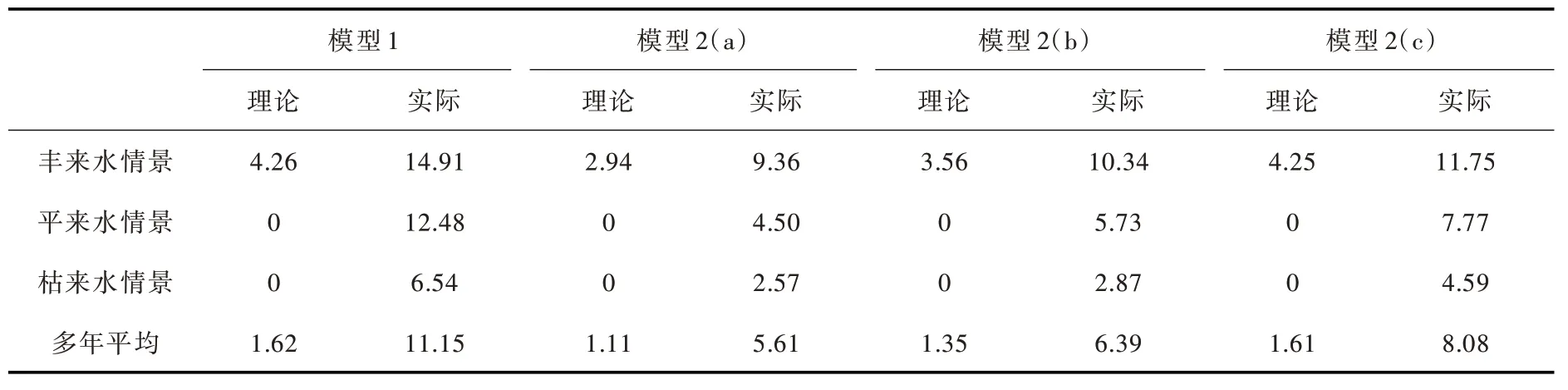
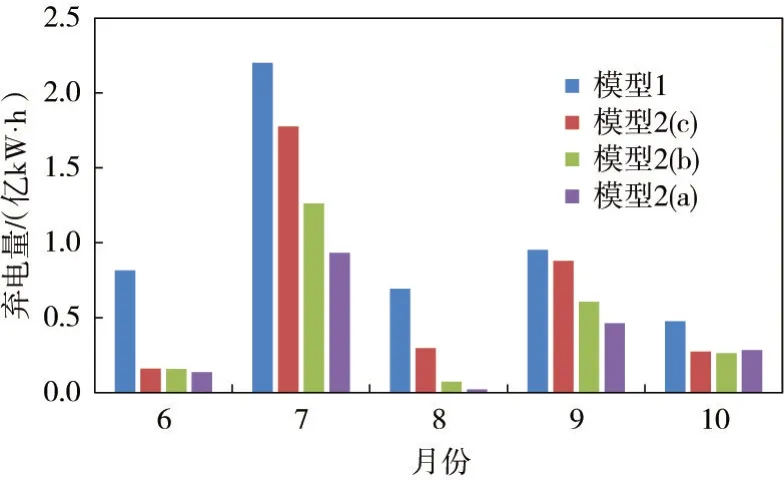
在确定的来水条件下,根据不蓄弃水Wt与拦蓄库容ΔVt的关系,日尺度蓄水可分为两种情况:(1)若Wt>ΔVt,说明弃水无法避免,月内日尺度蓄水均依据弃水风险最小规则ABDE 调度;(2)若Wt≤ΔVt,表明有足够的拦蓄库容,这种情况下,蓄水效益递增[16]。因此,月内日尺度蓄水应优先采用蓄水效益最大规则(图1 中ACDE)来抬高发电水头。令zdt 表示t 时段内d日末库水位,则应满足若d日及之前采用蓄水效益最大规则,则使发电效益最大的d 采用如下步骤确定:步骤1。令d=1;步骤2。逐日进行蓄水调度,d日及之前采用蓄水效益最大规则,d日之后采用弃水风险最小规则,求得步骤3。若且d 上述计算分析是在确定来水条件下得出的,拦蓄库容ΔVt根据长期调度模型确定。依据式(3),历史不同年份的径流资料均可计算得到Wt,对应的不蓄弃水流量为: 由于月内径流分布的随机性,长期调度计算给定月均入流qt时,所对应的水库不蓄弃水流量S ′t具有不确定性。为便于分析,本文将不确定变量S ′t定义为弃水风险评价指标,并采用历史径流资料统计得到qt与S ′t的相关数据集合,以分析两者的关系。 2.2 联合分布构建及弃水风险定量评价Copula 函数是一种构造多变量联合分布的有效方法,近年来被国内外学者广泛应用于多变量水文分析计算领域[17-19]。其理论优势在于可以灵活构建任意边缘分布的联合分布,并能够准确描述多变量间的相关性。下文基于Copula 函数构建上述月均入流与弃水风险的联合分布和条件概率分布,定量分析给定水库月均入流时的弃水风险并确定出置信区间。 2.2.1 Copula 模型选取及参数估计 假设随机变量X、Y 分别表示月均入库流量与弃水风险,其边缘分布函数分别为由二元分布的Sklar’s 定理[17]可知,X 和Y 的联合分布可以用Copula 函数C (u,v )表示: 式中:θ为Copula 函数参数; F (x,y )为具有边缘分布FX( x )和FY( y )的二元联合分布函数。 X 和Y 的联合概率密度函数表示为: 其中: 式中: c(u,v )为Copula 函数的密度函数; fX( x )和 fY( y )分别为随机变量X 和Y 的概率密度函数。 由于FX( x )和FY( y )的总体分布可能是不确定的,所以采用非参数核密度估计法得到样本的经验分布函数作为总体随机变量分布的近似。本文采用水文领域常用的Archimedean Copula(AC)方法[18-19],并选择三种典型的AC 函数构造月均入流与弃水风险的联合分布模型。 Gumbel Copula 函数: Clayton Copula 函数: Frank Copula 函数: 采用极大似然估计法确定上述三种Copula 函数的模型参数,并将每种分布与经验Copula 的平方欧式距离(ρ2)作为拟合优度的评价指标,以ρ2最小选择适合的Copula 函数作为月均入流与弃水风险的联合分布。 2.2.2 条件概率分布及置信区间估计 根据确定的Copula 联合分布函数,可以得到月均入库流量为特定值时弃水风险的条件概率分布: 相应的条件概率密度函数为: 根据 f ′Y|X( )y 绘制弃水风险条件概率密度曲线,如图3 所示。在曲线上可获得给定月均入流条件下所有可能的弃水风险及其概率, y′也可由曲线上的最高点确定得出。如图3 所示,给定置信水平1-α ,令弃水风险出现在左右两端的概率均为α 2 ,通过 f ′Y|X( )y 可计算出置信区间上、下限,如下式: 图3 条件概率密度曲线及置信区间估计 式中: yu、 yl分别为随机变量Y 的置信区间上、下限。 通过求解式(18)可得到置信水平为1-α 的区间估计[yl,yu],满足P(yl≤Y ≤yu)=1-α 。在[yl,yu]内Y 的值越大表示弃水风险越大,该置信区间可对弃水风险的不确定性进行定量评价。根据上述方法,给定X=x 可计算得到相应的y′、 yu和yl。将所有X 取值对应的y′相连可得到代表最可能弃水风险的关系曲线,同样的方法可得到yu和yl所对应的弃水风险置信区间上线和下线。 3.1 调度弃水计算长期调度蓄水期各月是否产生弃水取决于水库的拦蓄库容与时段内不蓄弃水量的大小关系。依据上文得到的弃水风险关系曲线,实际调度弃水估计如下: 其中: 若St表示长期调度时段t 的弃水流量,则根据2.1 节分析可知所以采用代表时段t 的实际弃水流量。 3.2 目标函数从发电侧角度出发,最大化发电量是水库优化调度常用目标之一,目的是尽可能提高水电发电效益[20]。以单个水库为例,传统发电量最大模型目标函数如下: 式中: E1为发电量目标,kW·h; Pt为时段t 电站平均出力,kW。 为避免发电调度中产生大量弃水,弃水损失常作为惩罚成本考虑到调度模型中[21],相应的目标函数如下: 式中: E2为考虑弃水风险后的发电量目标,kW·h; Plosst 为时段t 弃水损失出力,kW。 3.3 约束条件除满足式(1)蓄水期的水位约束外,优化模型还需满足下列水库运行约束: (1)水量平衡约束: 式中: Rt、Qt、 St分别为水库时段t 的平均出库、发电和弃水流量,m3/s。 (2)边界约束:主要变量的上下限约束和始末水位设置 (3)水电站发电函数: 式中: ht为时段t 发电净水头,m; φ(⋅) 为发电耗水率函数; Zttail为时段t 水电站平均尾水位,m;Ztloss为时段t 水电站发电水头损失,m。 (4)弃水损失出力函数: (5)水位-库容、尾水位-泄量关系曲线函数: 式中: fzv(⋅)为水库水位-库容关系函数; fzq(⋅)为水库尾水位-泄量关系函数。 3.4 模型求解采用逐步优化算法(POA)和离散微分动态规划算法(DDDP)的混合算法求解上述模型,详细求解过程见作者前期成果[22]。 需要提及,优化求解程序采用Java 语言编写,在每一步寻优中,通过罚函数法将模型中的不等式约束转化为惩罚项融入目标函数[23],使原问题转换为便于求解的无约束非线性规划问题。为了确保求解精度,水位-库容、尾水位-泄量、水头-耗水率等特性曲线以及弃水风险关系曲线均采用离散数值表达[24],并通过线性插值法实现变量间的相互转换。 4.1 工程背景小湾水库是澜沧江中下游梯级电站的“龙头水库”,总库容约150 亿m3,调节库容近100 亿m3,具有多年调节能力。小湾水电站装机容量4200 MW,正常高蓄水位为1240.00 m,死水位为1166.00 m,年均发电量约190 亿kW·h。小湾水库汛期(6—10月)来水相对集中,约占全年总入库的70%。作为控制性水库,小湾承担着重要的“蓄丰补枯”调节任务,其所在的梯级电站是云南电网最重要的调节电源。 本文以小湾水库为工程背景,1—12月为调度周期,其中6—10月为蓄水期。采用1990—2018年月尺度和日尺度入库流量资料作为优化模型输入条件进行模拟调度,水库调度期初水位和末水位均设置为1230.00 m。参考历史实际发电数据,调度期各时段最大发电流量设置为1900 m3/s。 4.2 月均入流与弃水风险关系采用历史月、日尺度入库流量资料分析蓄水期各月平均入流与弃水风险间的关系。由于6月和10月入库流量相对较小,采用2.1 节中式(3)计算的不蓄弃水在很多情景下为0,即这两个月弃水风险较小。因此,这两个月入库流量与弃水风险的关系在扣除不蓄弃水为0数据后,直接进行曲线拟合,如图4 所示。由于统计数据存在噪声,采用具有高精度和高效率优点的平滑样条拟合方法,平滑参数由确定系数(R-square)决定,要求R-square 大于0.99。7—9月平均入流与弃水风险间的联合分布采用2.2 节中介绍的Copula 模型构建,三种AC 函数的模型参数及优选指标见表1。可以看出,Gumbel Copula 函数的评价指标最优,说明Gumbel Copula 模型能更好的拟合月均入流与弃水风险的联合分布。 图4 月均入流与弃水风险关系拟合曲线 表1 Copula 模型参数及优选指标 采用2.2.2 节中方法,基于Gumbel Copula 联合分布模型得到月均入流为特定值时弃水风险的条件概率分布,并计算得到弃水风险80%置信区间及最可能值,图5 给出了7月份弃水风险置信区间的上线、下线及最可能值线。需要说明的是图中弃水流量估计为负值时修正为0;当月均入库流量特别大时,置信区间下线估计的弃水流量偏小,修正为式(5)月尺度计算的最小弃水量所对应的平均流量。 图5 弃水风险置信区间及最可能值 从图5 中可以发现,当7月平均入库流量在1200~3500 m3/s 区间时,弃水风险存在不确定性。当月均入流小于1200 m3/s 时,可认为没有弃水风险,而当月均入流大于3500 m3/s 时,不蓄弃水流量等于月均入流减去最大发电流量。根据风险置信区间可知随着月平均入流的增大,弃水风险不确定性逐渐减小,这是因为入库来水量级逐渐占据主导。同样地,根据8月份弃水风险置信区间得出弃水风险具有不确定性的流量区间为1300~4350 m3/s,9月份该区间为1300~3500 m3/s。 通过弃水风险置信区间估计,可得到7—9月水库平均入流与弃水风险间的关系曲线。在长期优化调度模型中可采用置信区间上线、下线和最可能值线评估调度弃水风险,其中上线表示80%置信水平下的极值风险,最可能值线代表条件最可能弃水风险。 4.3 模拟结果分析为了验证本文所提方法的有效性和可靠性,采用历史月入库径流资料进行模拟调度,并选择传统发电量最大模型作比较。此外,为了分析长期优化调度方案在指导实际运行中的弃水风险,将优化得到的各月末水位作为控制约束,采用日径流资料进行日尺度水库调度,作为实际运行的模拟。为了便于比较,将传统发电量最大模型和本文考虑弃水风险后的优化模型分别简称为模型1 和模型2。在评估弃水风险时,7—9月考虑风险置信区间上线、最可能值线和下线三种情况,对应的模型分别称为模型2(a)、模型2(b)和模型2(c)。 某一年历史径流模拟调度计算步骤如下:(1)以月入库流量为输入分别采用模型1、模型2(a)、模型2(b)和模型2(c)进行优化调度,得到对应的1—12月优化水位过程。(2)将月尺度的优化水位过程用于指导日尺度运行。为便于计算,枯期月内日水位过程通过均匀插值得到。蓄水期将月末水位作为日尺度蓄水调度的控制水位,根据不蓄弃水量和拦蓄库容间的关系,采用2.1 节中介绍的确定来水条件下蓄水方式确定日水位过程。(3)以日入库流量为输入,按照步骤2 确定的日水位过程进行“以水定电”计算即可得到逐日发电量和弃水等结果。(4)统计月尺度和日尺度的全年调度数据,分别作为理论计算和实际运行的结果。 为了便于分析,根据水库年径流资料确定来水频率曲线(皮尔逊Ⅲ型),将1990—2018年划分为丰(P≤37.5%)、平(37.5% 4.3.1 可靠性分析 以模型1 优化得到的月尺度水位过程为基础,分别采用弃水风险80%置信区间上线和下线估计实际调度弃水。历史来水资料模拟实际运行的弃水情况与置信区间估计结果比较如图6所示,不同来水情景统计结果见表2。 图6 真实弃水与风险置信区间估计结果比较 表2 不同来水情景弃水估计(单位:亿m3) 对比模型1 实际运行弃水结果,丰、平、枯来水情景下弃水风险置信区间下线估计的弃水量较实际弃水少,而上线估计的弃水量较实际弃水多。弃水风险80%置信区间包含了超过90%来水年的弃水真实值,表明该置信区间估计是可靠的[18],可以用来评价弃水风险的不确定性。 4.3.2 不同模型结果比较 不同模型模拟调度的发电和弃水统计结果分别见表3 和表4。可以看出不同来水情景的优化方案在指导水库实际运行时均会产生弃水和电量损失,其中尤以丰水情景损失最多。例如模型1,其实际运行与理论计算相比,多年平均发电量减少约4.12 亿kW·h,弃水增加约9.53 亿m3。不同来水情景下,模型2 理论计算发电量和弃水与实际运行结果相比偏差更小,其中模型2(a)偏差最小。 表3 不同模型发电结果对比 (单位:亿kW·h) 表4 不同模型弃水结果对比 (单位:亿m3) 模型2 的理论计算发电量小于模型1,但其优化方案在实际运行中的弃水更少、发电量更多:其中模型2(a)考虑了极值风险,实际运行弃水最小;模型2(b)实际运行发电量最大,模型2(a)除了丰水情景整体上也较模型1 发电量多。从发电效益最大化角度,模型2(b)最佳,与模型1 相比,多年平均弃水减少约4.76 亿m3、发电量增加约1.15 亿kW·h。因此,宜采用弃水风险置信区间最可能值作为蓄水期的弃水风险估计。 统计模拟实际运行的弃水结果,参考式(30)计算弃电损失,得到不同模型蓄水期各月平均弃电量如图7 所示。可以看出,考虑弃水风险后蓄水期各月均可有效减少弃电损失。不同模型丰、平、枯来水情景的水库平均蓄水过程见图8,可以发现考虑蓄水期的弃水风险后,不仅蓄水期水位降低,消落期水位也随之降低。其中5月末,即连接消落期和蓄水期的汛前水位,受弃水风险的影响最大。以模型2(b)为例,丰、平、枯来水情景5月末水库蓄水量较模型1 分别减少7.5 亿、9.8 亿和7 亿m3,相应的库水位分别降低6.24、6.35 和4.15 m。模型1 理论发电量最大,优化水位较高,但存在较大的弃水风险,难以满足实际应用。模型2 对弃电损失进行了惩罚,为了避免弃水,水库在汛前腾出更多库容,使得整体运行水头降低,虽然导致理论发电量减少,但却更接近实际运行需求。 图7 不同模型蓄水期各月平均弃电量 图8 水库蓄水量过程 综合上述分析可知,以月平均径流为输入得到的水库长期优化调度方案与实际运行偏差较大,在实际运行中存在较大的弃水风险,进而造成电量损失。考虑弃水风险后的优化方案可以有效减少实际运行中的弃水并增加发电量,更具可操作性。 本文考虑日尺度径流波动对水库长期调度决策的影响,提出一种蓄水期弃水风险定量评价方法,并以此为基础建立了考虑蓄水期弃水风险的水库长期发电调度模型。选择澜沧江流域控制性水库小湾为实例背景,通过模拟调度分析,得到如下主要结论:(1)构建的弃水风险指标可以有效量化水库长期调度蓄水期的弃水损失;(2)基于Copula 函数的条件概率分布能定量评价特定月均入流条件下的弃水风险并给出具有概率特征的置信区间;(3)在弃水风险置信区间内,宜采用最可能估计值作为长期调度决策的依据;(4)所提考虑弃水风险的优化模型可有效减少调度方案弃水风险,更具可操作性,与传统方法相比,可使多年平均弃水减少约4.76 亿m3、发电量增加约1.15 亿kW·h。



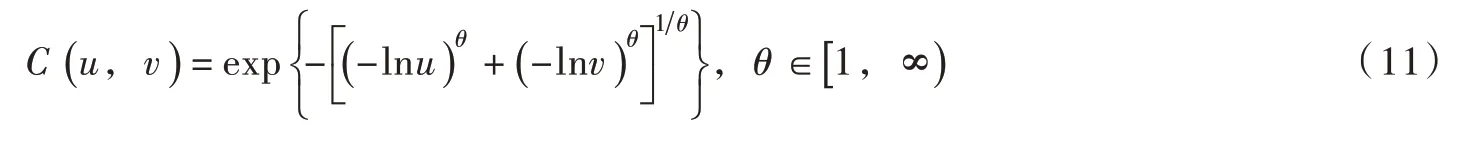
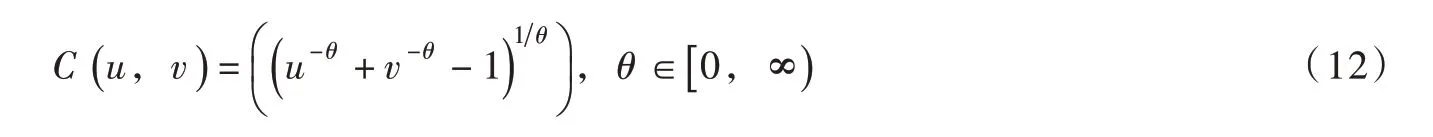
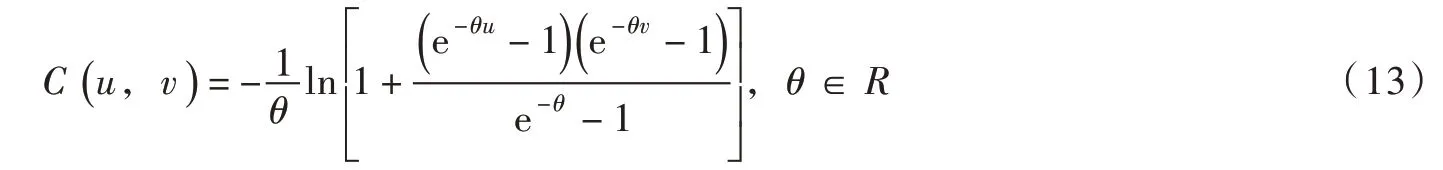


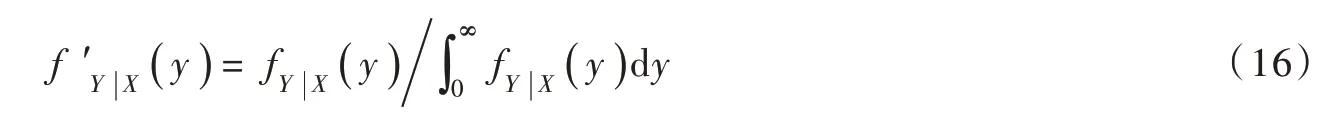



3 考虑蓄水期弃水风险的发电调度模型
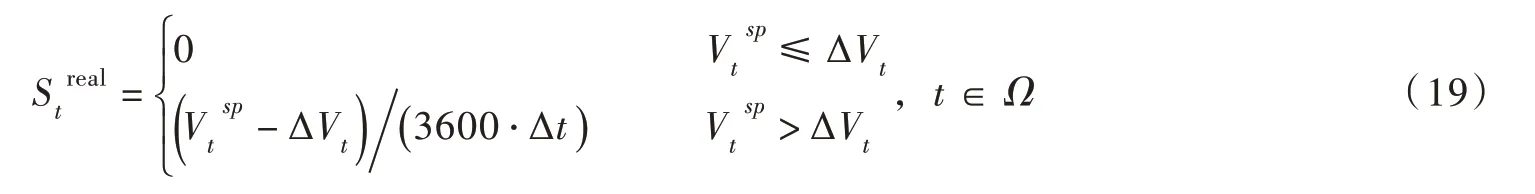








4 实例分析






5 结论

