逻辑推理素养在解析几何的评价模型和应用*——以“解析几何一类定值定点问题”为例

广东省汕头市第一中学(515000) 许秋妍

1 逻辑推理素养的内涵、主要形式及学习价值

《普通高中数学课程标准(2017年)版》提到,逻辑推理是指从一些事实和命题出发,依据规则推出其他命题的素养.主要包括两类: 一类是从特殊到一般的推理,推理形式主要有归纳、类比;一类是从一般到特殊的推理,推理形式主要有演绎.通过高中数学课程的学习,学生能掌握逻辑推理的基本形式,学会有逻辑地思考问题;能够在比较复杂的情境中把握事物之间的关联,把握事物发展的脉络;形成重论据、有条理、合乎逻辑的思维品质和理性精神,增强交流能力[1].

2 逻辑推理素养在解析几何的评价模型

2.1 评价理论基础

2.1.1 SOLO 评价理论

SOLO 的理论基础是皮亚杰的发展阶段学说,由著名教育心理学家比格斯(Biggs)教授及其同事经过长期的研究和探索提出,是一种以等级描述为特征的质性评价方法.SOLO分类法关注认知过程,而不仅仅是认知结果,认为分析学生针对某项具体任务的反应是描述学习进步和认知结构的最佳方法.比格斯在分析了大量学生回答各学科问题的反应时发现,个体的反应按结构复杂性的层次变化的特点.因此,把这种层次变化划分为5 种水平: 前结构水平(Prestructural level,P),单一结构水平(Uni-structural level,U),多元结构水平(Multi-structural level,M),关联水平(Relational level,R),抽象扩展水平(Extended Abstract level,EA).

SOLO 分类法从能力、思维操作、一致性与收敛和应答结构4 个方面对学生的回答分成5 种水平.其中,思维操作是指把线索和回答联系起来的方式,例如是同义反复呢还是进行了归纳或者是进行了真正的合乎逻辑的演绎[2]?

2.1.2 高中数学课程标准

课程标准对逻辑推理进行了三个水平的划分,分别指向学业考试水平、高考水平和自主招生考试水平,每个水平中对其提出了若干要求.其中水平一提出“了解熟悉的数学命题的条件与结论之间的逻辑关系;掌握一些基本命题与定理的证明,并有条理地表述论证过程”,水平二提出“能够在关联的情境中,发现并提出数学问题,用数学语言予以表达;能够对与学过的知识有关联的数学命题,通过对其条件与结论的分析,探索论证的思路,选择合适的论证方法予以证明,并能用准确的数学语言表述论证过程”,水平三提出“能够掌握常用逻辑推理方法的规则,更理解其中蕴含的数学思想”等.

课程标准在平面解析几何这一单元的教学中提示教师要引导学生经历借助几何图形的特点,形成解决问题的思路,通过直观想象和代数运算得到结果,并给出几何解释,解决问题等过程;课程标准也对学生也提出了学业要求: 能够掌握平面解析几何解决问题的基本过程,重点提升逻辑推理等五个方面的核心素养[1].

2.2 逻辑推理素养在解析几何的评价模型

基于SOLO 评价理论,结合课程标准的要求,笔者对逻辑推理素养在解析几何的评价模型进行如下设计:

?

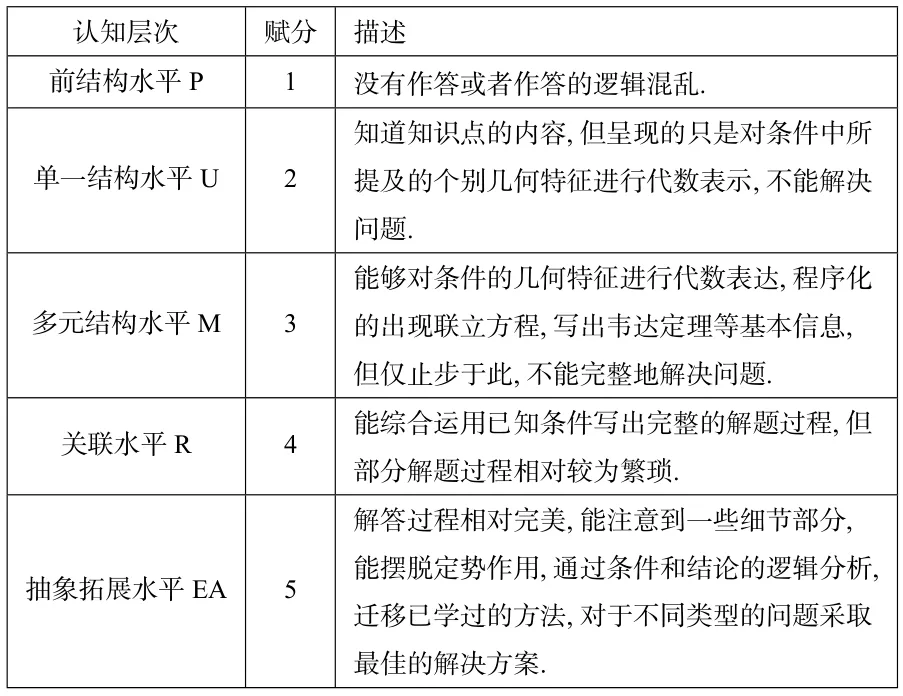
3 评价模型在实验研究中的应用

3.1 研究目的和设计

3.1.1 研究的目的

根据逻辑推理素养的评价模型,评价学生在解决解析几何一类定值定点问题时,运用逻辑推理素养对条件与结论的分析、归纳,并对解题方法的迁移等所达到的认知水平.

3.1.2 研究的自变量、因变量和控制变量

自变量: 逻辑推理素养的认知水平.

因变量: 学生的数学学业成绩,数学能力,非智力因素等.

控制变量: 学生的学习态度、习惯,已掌握的解题方法,教师的教学风格等.

3.1.3 实验的模型

3.2 研究过程

3.2.1 被试选择

笔者所任教的班级学生,共45 人.选择的原因在于这个班级的高考选考组合是物理、化学、生物,学生的学习态度积极,数学能力整体较好,在平时年级测验中名列前茅;学生对笔者教学风格的适应已有半个多学期.以上这些都能较好的减轻控制变量对实验结果的影响.

3.2.2 实验前测试

学生已经完成直线与圆锥曲线的综合题通性通法的学习,完成以下A 组三道测试题:

A1: (已知过定点的直线与圆锥曲线相交,证明两直线斜率之和(积)为定值)已知椭圆C:=1 过右焦点F作直线l交椭圆C于A、B两点(异于左右顶点),椭圆C的左顶点D,试判断直线AD的斜率与直线BD的斜率之积与的大小,并说明理由.

A2: (已知两直线斜率之和(积)是定值,证明直线斜率为定值)已知抛物线C:y2=4x上有一点P位于x轴的上方,若PA、PB的倾斜角互补,分别交曲线C于A、B两点(点A、B、P不重合),试判断直线AB的倾斜角是否为定值,若是,求出此值,若不是请说明理由.

A3: (已知两直线斜率之和(积)是定值, 证明直线过定点)已知抛物线E:y2= 2x恰好经过等腰梯形ABCD的四个顶点,AB//CD,AD的延长线与抛物线E的准线的交点证明:BD经过抛物线E的焦点.

3.2.3 源题训练——学习“构造齐次方程”解法

主要教学流程: 笔者重点讲解用“构造齐次方程法”[3]解决A1 题,帮助学生理解“构造齐次方程”法与通性通法的异同点,重点在构造齐次方程这一关键步骤,引导学生分析A组三道题条件与结论之间的逻辑关系,思考能否把该方法迁移解决其他问题.

在源题训练中,笔者重点讲授“构造齐次方程法”的设计意图是因为学生已经学习了通性通法解决圆锥曲线的综合题,为了减轻这个控制变量对实验结果的影响,能够更清晰地判断在学生解答后续靶题的过程中,是否运用了逻辑推理素养对问题的条件和结论进行分析、类比,并将解题方法进行迁移等,也为了更好地评价学生在经历上述逻辑思维过程中所达到的认知层次.

3.2.4 靶题测试

靶题即B 组3 道题的设计分别对应A 组3 道题,目的是为了便于对学生的认知水平进行横向和纵向的比较.

B1: (已知过定点的直线与圆锥曲线相交, 证明两直线斜率之和(积)为定值)已知椭圆= 1 上一点A(−2,−1),过点B(−4,0)作直线l交椭圆C于M、N两点.证明:MA、NA的斜率之和为定值.

B2: (已知两直线斜率之和(积)是定值,证明直线斜率为定值)已知椭圆= 1 上一点M、N是椭圆上两个动点,若MA的斜率和NA的斜率互为相反数,证明直线MN的斜率是定值,并求出这个定值.

B3: (已知两直线斜率之和(积)是定值, 证明直线过定点)已知椭圆C:+y2= 1 的短轴的上顶点P,斜率为k的直线l不经过P点且与椭圆C交于E,F两点,设直线PE,PF的斜率分别为k1,k2,且k1+k2=−1,试问直线l是否过定点? 若是,求出这定点;若不存在,请说明理由[4].

3.3 结果与分析

3.3.1 实验前测试的结果和分析

根据评价模型, 对学生的实验前测试进行评价, 并对5个层次的人数进行统计得到图1;A 组三道题学生的评价赋分平均值依次为3.5,2.36,2.73.

图1

从以上数据可以看出学生完成A1 题情况更好些,能达到关联结构等高层次认知水平的人数更多.笔者通过查阅学生卷面情况,结合数据发现,出现这种情况的原因在于A1 题由条件出发更容易让学生联系到用通性通法——设而不求、韦达定理进行求解,学生对这种解法轻车熟路,数学运算素养在过往学习中获得较好的提升,完成这道题的成功率也就更高些;但A2、3 题则不同,它们的条件都是两条过定点的直线分别与曲线相交,这使得通性通法行不通,需要两次联立直线与曲线方程,分别求出交点坐标,从而求得直线的斜率或者方程.这种解法需要学生更高的运算能力和化简技巧,导致完成率不高,逻辑推理的认知水平也较低.

3.3.2“构造齐次方程”法掌握的结果和分析

根据评价模型,对学生的A1、B1 测试情况进行评价,对5 个层次的人数进行统计,并对两种解法的掌握情况进行比较得到图2; 学生在A1、B1 的评价赋分平均值分别为3.5,3.89.

图2

由图2 和数据可以看出,学生对“构造齐次方程”这种新方法的接受情况较好,通过短时间的训练可以达到与使用通性通法解题相当甚至更高的认知水平,尤其减少了前结构水平的人数,说明被试对象对学习新知识的兴趣浓厚,拥有挑战难题的决心,这对后续教学中如何帮助后进生的学习数学起到启示作用.

数据中不排除有学生对新方法的掌握只是停留在同义反复的阶段,即对B1 的解答仅是对源题训练中的例题解法“依样画葫芦”,那么,这种情况对提升学生的逻辑推理素养并没有起到提升作用.

3.3.3 运用逻辑推理素养的结果与分析

学生在解答B2、3 两题时,要首先对条件与结论的分析、归纳和推理,类比源题训练中的例题,才能迁移“构造齐次方程”法完成解答.为了能让评价结果能更清晰地显示学生经历以上逻辑推理过程的不同水平,并与用通性通法解答的评价结果进行清晰对比,同时筛查出前面提到的“同义反复”等逻辑推理不良情况,笔者认为在解答中能使用新方法并完整得到解答过程的在认知水平上已达到拓展的阶段,因此将这种答题情况评价为“抽象拓展结构”,赋分为5 分.

根据评价模型,对学生的B2、3 测试情况进行评价,并对5 个层次的人数进行统计,将A2 与B2 的数据进行对比得到图3,将A3 与B3 的数据进行对比得到图4,将B1-3 的数据进行对比得到图5.

图3

图4

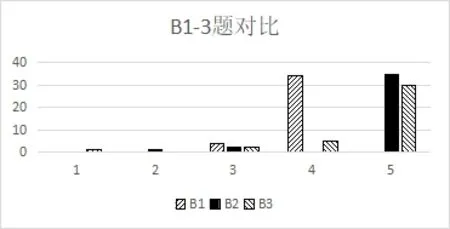
图5

由图3 和图4 可以看出,学生将新方法迁移到其他问题上的能力有了很大的提升,说明较多学生在源题训练中对新方法的学习不是死记硬背,而是能够理解新方法的来龙去脉,从而才能将新方法迁移到其他类型问题的解答.由图5 可以看出,学生不论是对新方法的掌握还是迁移所达到的认知水平都是相当的,说明学生对新方法学习的积极性很强,高涨的学习热情对挑战一类问题、提升学生核心素养起到推动作用.

由图3 和图4 还可看出,少数学生出现了前面所分析到的“同义反复”情况.这部分学生因为没有完全理解新方法,从而无法进行迁移;他们在解答中只能列举出部分条件,但无法对条件进行整合得到完整的解答过程, 认知水平较低,个别学生甚至出现了前结构水平这种认知水平倒退的情况.从中可以看出,这种评价方式能筛选出认知水平较差的学生,这给后续的针对性辅导提供了参考意见.

4 结论与反思

4.1 评价模型的设计反思

基于SOLO 理论设计的评价模型对学生的逻辑推理素养的认知水平进行划分,可以帮助教师更精准地了解学生的认知水平分布情况和学生在解答中普遍存在的问题,帮助教师改进教学.

它可以作为过程性评价,在教授解析几何中的某个知识点或方法时,教师用于评价学生学习解析几何过程中逻辑推理素养的水平.它还可以帮助学生了解自己认知水平和学习过程中存在的逻辑推理问题, 规范其数学语言和推理过程,深度理解逻辑推理过程中蕴含的数学思想方法,提升自身逻辑推理素养水平[5].

本评价模型作为一种评价工具,那么它的适用范围能否推广到学校甚至更大的区域,适用的持续性能否贯彻整个高中的解析几何学习过程,这些不足仍有待进一步研究.

4.2 逻辑推理素养提升的教学思考

解析几何的研究对象是几何图形,所用的研究方法主要是代数方法.在学生解决解析几何综合题时,因为其对知识的综合性和运算技巧等要求高的原因,经常止步于将几何图形代数表示, 程序化地罗列出韦达定理等基本步骤, 即处于多元结构水平.如何将学生的逻辑推理素养提升到更高的水平一直是师生突破的难关.笔者认为解决这个问题不能靠“刷题”来实现,这种疲劳战术只会进一步消耗学生对解决解析几何难题的决心,而无法打通解决问题的“关卡”.此外,在研究中还发现学生的学习积极性影响着他们的学习效果.

综合以上, 笔者认为在教授解析几何综合题的过程中,教师要先有意识地研究综合题,尤其是高考题,发现其规律并进行分类,然后在开展探究课、小组合作的研究性学习等教学活动解决某一类综合难题.一方面它能给予学生特别的解法“亮点”,让学生对学习新知充满动力;另一方面,探究活动能改变满堂灌、被动接收知识,它能引导学生在其中运用逻辑推理能力,理清问题条件与结论的逻辑关系,领悟一题多解或者通性通法的关键点,从而积累更多有效的逻辑推理经验和解题方法.这些教与学的活动都能帮助学生提升逻辑推理素养,增强面对难题的信心和能力.