GeoGebra辅助立体几何教学的原则、实践与反思

江苏省常州市第二中学(213000) 王 强

新一轮课程改革以来, 信息技术成为了一个重要词汇,如何实现信息技术与数学课程的深度融合成为了一个重要课题.立体几何是研究三维空间中物体的大小、形状和位置关系的一门数学学科,由于其高度抽象性和需要较高的空间想象能力,一直是教学的重难点.一批优秀的数学软件如几何画板、GeoGebra 为突破立体几何中的重难点提供了有利工具,GeoGebra 软件更是凭借3D 功能,将一些抽象的几何图形通过直观演示变得直观可见.因此,研究GeoGebra 与立体几何教学的融合对改善立体几何教学效果有重要作用.

本文结合苏教版“空间几何体的表面积”这一节中的圆柱、圆锥、圆台部分谈谈应用GeoGebra 辅助立体几何教学的策略、实践与反思,供同行参考.

1 应用原则

1.1 简便性与简洁性相结合

利用GeoGebra 创设教学动画,操作要简便.同时,要注意操作界面的简洁性,一些不需要展示的对象可以隐藏,降低学生的认知负荷.

1.2 适度性与整合性相结合

教学中应用GeoGebra 软件进行教学要适度,确实对教学起到促进作用的如板书作图效果不佳的或涉及到平移、旋转等需要动态观察的可以用GeoGebra 呈现和制作功能这一优势,降低学生理解难度.

1.3 动态演绎与静态作图相结合

立体几何中与运动问题相关的概念或直接作图不便的问题,可以利用GeoGebra 的3D 绘图区功能制作动画或图片辅助课上教学.随着学习的深入,就要逐渐脱离信息技术呈现图形来建立空间观念.对几何体的认知不能仅停留在看图,更要会自己绘图,亲历立体图形画在平面图形上的过程,提升直观想象的核心素养.

1.4 实验归纳与演绎推理相结合

GeoGebra 辅助立体几何教学最明显的优点是为学生创设三维的研究情境,让学生经历动手操作自主探究,通过软件操作,发现规律提出猜想.但是,不能使立体几何的教学停留在浅层次的操作,更要上升到深层次的演绎推理层次.只有将实验归纳与逻辑演绎相结合,才能发挥GeoGebra 辅助立体几何教学的优越性.

2 教学过程设计

2.1 问题导入——活动阶段

师: 生活中我们可以将一张纸折成圆柱或圆锥的形状,那么反过来圆柱、圆锥和圆锥的侧面可以沿其母线剪开后展在平面上,这时展开图的面积就是它们的侧面积.

问题1沿圆柱的一条母线将其剪开后展在平面上,则圆柱的侧面展开图是什么形状? 圆柱的侧面积是多少?

2.2 问题探究——过程阶段

师生活动: 教师利用GeoGebra 带领学生感受沿圆柱的母线剪开后展在平面的过程, 通过观察可以发现展开图是矩形, 矩形的长是底面圆的周长, 宽为圆柱的母线长, 所以S圆柱侧=cl=2πrl.

图1

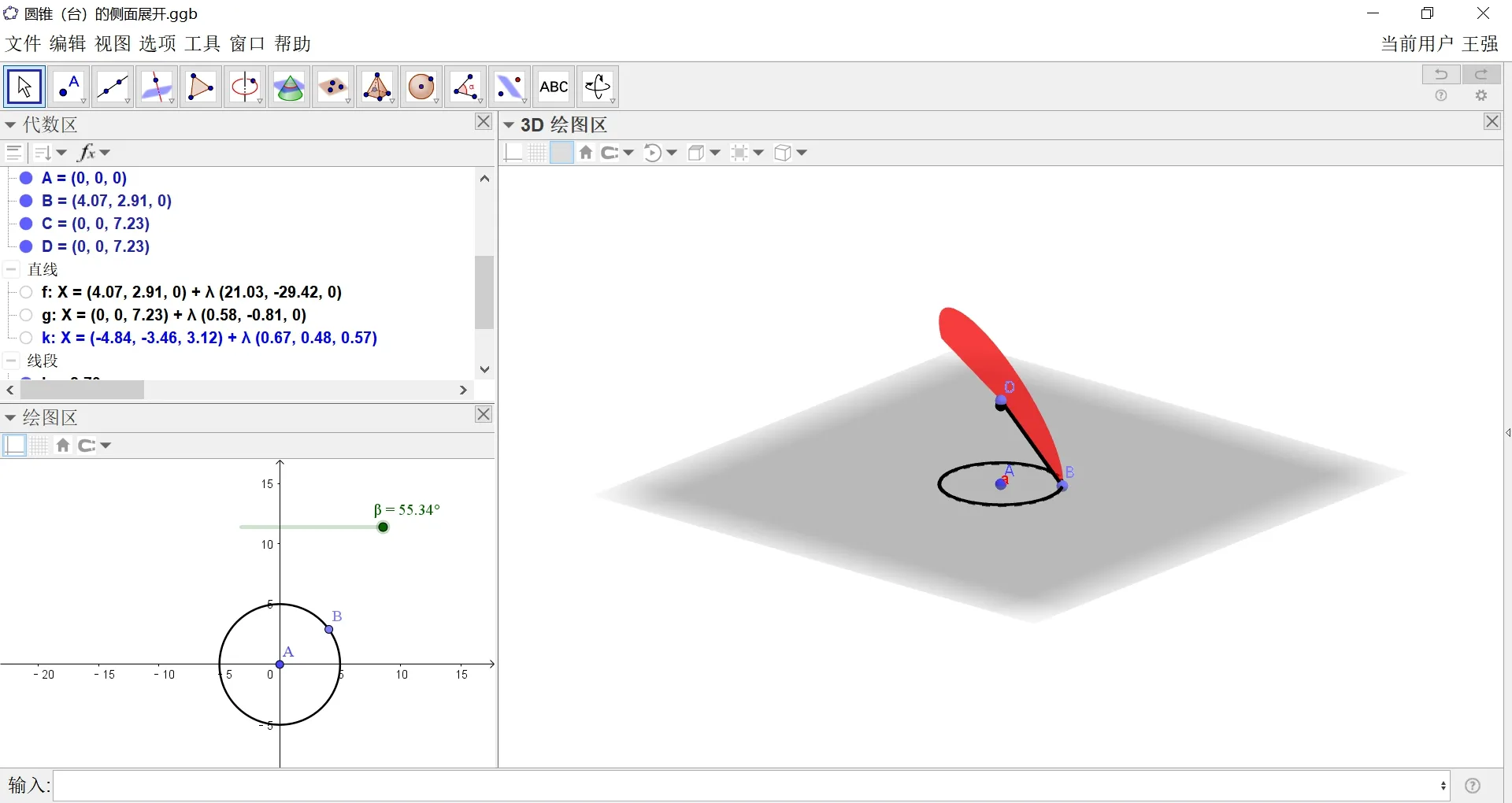
图2

问题2沿圆锥的一条母线将其剪开后展在平面上,则圆锥的侧面展开图是什么形状? 圆锥的侧面积是多少?

师生活动: 学生先直观想象, 图形是扇形.教师利用GeoGebra 带领学生感受沿圆锥的母线剪开后展在平面的过程,通过观察可以发现展开图是扇形,扇形的弧长是底面圆的周长,半径为圆锥的母线长,所以=π·l.

例1已知圆柱的高和底面半径分别为a和b，求其侧面积.

例2已知圆锥的底面直径与高都是2,求该圆锥的侧面积.

例3以一个圆柱的下底面为底面,并以圆柱的上底面圆心为顶点作圆锥,若所得的圆锥底面半径等于圆锥的高,则圆锥的侧面积与圆柱的侧面积之比是多少?

设计意图利用GeoGebra 制作圆柱、圆锥的侧面展开图,突破以往教学中学生只能凭空想象的困境,让学生直观感知到侧面展开图与侧面积的关系,培养空间想象能力.

问题3沿圆台的一条母线将其剪开后展在平面上,则圆台的侧面展开图是什么形状? 圆台的侧面积是多少?

师生活动学生先直观想象, 图形是扇环.教师利用GeoGebra 带领学生感受沿圆台的母线剪开后展在平面的过程, 通过观察可以发现展开图是一段扇环, 扇环的一段弧长是上底面圆的周长, 另一段弧长是上底面圆的周长,还有两条边的长等于圆台的母线长.师生合作探究, 借助将圆台的侧面积转化成圆锥的侧面积的方法, 推导出教师引导学生类比梯形的面积公式进行记忆,并利用分割的方法和极限的思想阐明这样记忆的合理性.

图3

2.3 问题解决——对象阶段

问题4圆柱、圆锥和圆台的侧面积公式之间有怎样的关系?

图4

学生直观想象后,教师借助GeoGebra 动态呈现圆柱、圆台、圆锥的相互转化,让学生体会数与形的和谐统一.

设计意图教学中利用信息技术展示空间图形,为学生理解圆柱、圆锥和圆台的侧面积公式之间的相互联系提供几何直观.

图5

例4一个直角梯形上底、下底和高之比为2 : 4 :将此直角梯形以垂直于底的腰为轴旋转一周形成一个圆台, 求这个圆台上底面积、下底面积和侧面积之比.

通过侧面展开来求圆柱、圆锥和圆台的侧面积,可以将空间图形问题转化为平面图形问题,这是解决立体几何问题中最基本的、常用的方法,也就是我们说的降维的思想.

思考题已知圆柱CA的底面半径为2cm, 母线长为8cm 有一蚂蚁从底面圆周上一点B出发,沿侧面爬行一周后到达同一母线的另一端点D,则爬行最短路径长为多少?

2.4 知识构建——图式阶段

问题5通过刚刚的学习,你掌握了哪些知识? 体会到哪些研究方法?

学习了圆柱、圆锥和圆台的侧面积公式,体会到降维和转化的研究方法,并感受到用联系的眼光看问题.

设计意图通过本节课的小结,让学生构建自己的知识结构,培养反思的习惯.

3 教学设计反思

(1)本节课的教学设计利用直观想象、操作确认的方式展开研究,借助类比归纳的思维方法,在GeoGebra 的辅助下通过动态呈现侧面展开的过程,增强学生对展开图的面积即为侧面积的认识,培养直观想象的核心素养,进一步感受“空间问题平面化”这种降维转化的研究方法.

(2)利用GeoGebra 的3D 平台,通过滑动条的设置,为学生理解和掌握柱体、锥体、台体的侧面积公式的联系提供了几何直观,化“无形”为“有形”,从“数”与“形”的双重表征促进学生对知识的深度理解.

4 GeoGebra 案例制作过程

4.1 圆柱的侧面展开

第一步: 用指令输入一个圆柱即指令栏输入“圆柱((−1,0,0),(−1,0,4),1)”,

第二步: 设置滑动条控制展开的程度;

第三步: 指令栏输入曲面指令“如果(k=0, 曲 面(0,u,v,u,0,2,v,0,4), 曲 面(r(−1 + cos(kθ)),rsin(kθ),h,θ,0,2π,h,0,4)”.

4.2 圆台(锥)侧面展开

步骤一: 创设底面

(1)指令栏输入“(0,0,0)”,得到点A;

(2)指令栏输入“圆周(A,5,z轴)”,得到以A为圆心,5为半径且与z轴垂直的圆c;

步骤二: 构造上底面上一点

(1)用描点工具,在圆c上任取一点B;

(2)用描点工具,在z轴上任取一点C;

(3)指令栏输入“描点(线段(B,C))”,得到线段上BC上的一动点D;

(4)指令栏输入“圆周(z轴,D)”,得到垂直于z轴且过D点的圆;用工具栏中的线段工具,连接线段BD;

步骤三: 做辅助直线

(1)指令栏输入“垂线(B,平面(A,B,C))”,得到过点B且垂直于平面ABC的垂线f;

步骤四: 做辅助角

(1)指令栏输入“sin(z(C)/距离(B,C))”,得到∠CBA的大小α(注: 输入-1应按住“Alt”键,然后输入−1 即可);

(2)设置滑动条角度β,右击设定其属性中取值范围为0到α,增量为0.01;

步骤五: 构造旋转曲面

(1)指令栏输入“旋转(z轴,−β,g))”,表示z轴绕直线g旋转−β角,改变旋转后直线名称为k;

(2)指令栏输入“曲面(曲线(mB+(1−m)D,m,0,1),(2π距离(A,B))/距离(B,k),k)”,得到侧面展开图a.

步骤五: 美化和操作

(1)将曲面a的颜色设为红色,样式中线径调为0;隐藏直线f,g,k;隐藏3D 坐标系;将β的值调为0;

(2)移动D点到C点的位置,拖动β,实现圆锥的侧面展开;移动D点在BC之间,拖动β,实现圆台的侧面展开.

4.3 圆柱圆锥圆台的联系

步骤一: 设置基本量

利用滑动条功能依次设置数值a(控制上底面圆的半径,取值范围最小值改为0),数值b(控制下底面圆的半径,取值范围最小值改为a),数值h(控制高,取值范围最小值改为0),角度α(控制旋转程度的大小);

步骤二: 构造几何体的底面和侧面

(1) 构造侧面: 指令栏输入“曲面((a+ (b −a)(h −t)/h)cosθ,(a+(b −a)(h −t)/h)sinθ,t,t,0,h,θ,0,α)”,得到曲面c,设置其属性,样式中线径调为0;

(2)构造上底面: 指令栏输入“曲面(r∗cosθ,r∗sinθ,h,r,0,a,θ,0,α)”,得到曲面d,设置其属性,样式中线径调为0;

(3)构造下底面: 指令栏输入“曲面(r∗cos(θ),r∗sin(θ),0,r,0,b,θ,0,α)”,得到曲面e,设置其属性,样式中线径调为0;

步骤三: 美化和操作

(1)隐藏3D 空间坐标系;

(2)若a的值为0,b不为0,则移动α,生成圆锥;若b和a的值相等且都不为0,则移动α,生成圆柱;若b和a的值不等且都不为0,则移动α,生成圆台.