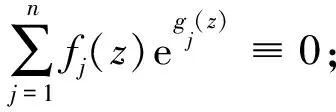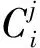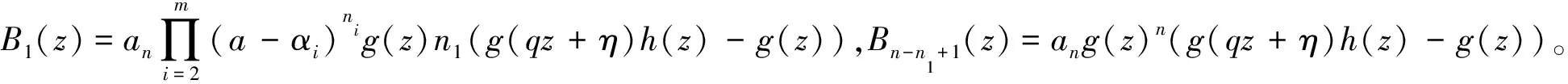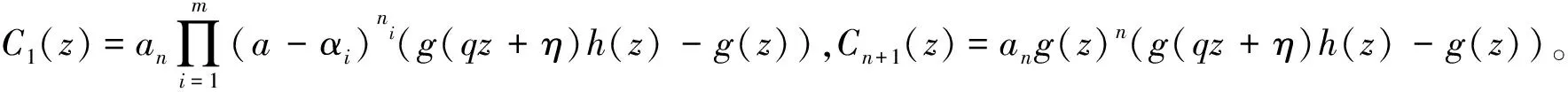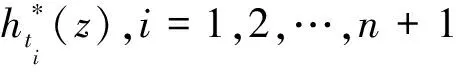一类复q-平移差分-微分多项式的值分布

郑秀敏，占美龙

(江西师范大学数学与统计学院，江西 南昌 330022)

1 引言与结果

本文中，我们使用Nevanlinna理论的标准记号和基本结果(见文[1-3])。若无特殊说明，亚纯函数是指在整个复平面上亚纯的函数。我们用记号σ(f)表示f(z)的级，用记号λ(f-c)表示f(z)-c的零点收敛指数，其中c∈∪{∞}。

众所周知，在亚纯函数值分布理论的研究中，微分多项式的值分布研究是一个经典问题。该问题源自W.K.Hayman在文[4]中提出的猜想:当f(z)为超越亚纯函数且n∈+时，f(z)nf′(z)取任意非零复数无穷多次。随后，许多学者致力于对复差分多项式的值分布进行研究，得到了许多有意义的结果。这些结果可视为相应复微分多项式值分布结果的差分模拟。其中，文[5]和文[6]中的结果可以看作是上述W.K.Hayman经典结果的最直接的差分模拟结果。2014年，郑秀敏和徐洪焱在文[7]中研究了Valiron-Mokhon’ko定理的微分-差分模拟结果，并运用该结果研究了某类微分-差分多项式的亏量。同时，上述结果可进一步推广至q-差分情形和q-平移差分情形，具体可见以下两个结果。

2011年，刘凯和祁小光在文[8]中研究了q-平移差分多项式f(z)nf(qz+η)的值分布，得到了以下结果。

定理A[8]设f(z)为零级超越亚纯函数，q为非零复常数。则当n≥6时，q-平移差分多项式f(z)nf(qz+η)取任意b∈{0}无穷多次。

2013年，涂金和郑秀敏在文[9]中将条件“n≥6”减弱到“n≥5”，改进了定理A。

注意到定理A中考虑的是f(z)具有零级的情形。由此，我们自然提出问题:当f(z)具有正有穷级时，结果又会怎样?对于该问题，徐娜等在文[10]中研究了q-差分-微分多项式[f(z)f(qz)](k)的值分布，其中f(z)为具有正有穷级的超越整函数，得到结果如下。

定理B[10]设f(z)为超越整函数且满足0<σ(f)<∞，a为f(z)的有穷Borel例外值，q∈{0，1}且使得qσ(f)≠±1。记H(z)=[f(z)f(qz)](k)，则以下结论成立。

(1) 若a=0，则0亦为H(z)的Borel例外值，即H(z)没有非零有穷Borel例外值。

(2) 若a≠0，则H(z)没有有穷Borel例外值。

(3)H(z)取任意c∈{0}无穷多次，且满足λ(H-c)=σ(f)。

受定理A和定理B的启发，我们考虑形式更一般的q-平移差分-微分多项式的值分布。一方面，我们用q-平移差分f(qz+η)和f(qz+η)-f(z)替代f(qz)。另一方面，我们将f(z)推广为f(z)的多项式。在叙述所得结果之前，我们先引入以下记号。设

P(z)=anzn+an-1zn-1+…+a1z+a0，n∈+

为非零多项式，其中a0，a1，…，an(≠0)为复常数。又记m∈+为P(z)的不同零点个数，则P(z)可以表示成

P(z)=an(z-α1)n1…(z-αm)nm

其中α1，α2，…，am∈为P(z)的不同零点，n1，n2，…，nm∈+且满足

首先，我们考虑q-平移差分-微分多项式[P(f)f(qz+η)](k)的值分布，推广了定理B。

定理1.1设f(z)为超越整函数且满足0<σ(f)<∞，a为f(z)的有穷Borel例外值，η∈，q∈{0，1}且使得qσ(f)≠-1，-2，…，-n。记

H1(z)=[P(f)f(qz+η)](k)，k∈+

则H1(z)没有非零有穷Borel例外值，即H1(z)取任意c∈{0}无穷多次，且满足λ(H1-c)=σ(f)。

其次，我们用f(qz+η)-f(z)替换f(qz+η)，得到相应结果如下。

定理1.2设f(z)为超越整函数且满足0<σ(f)<∞，a为f(z)的有穷Borel例外值，η∈，q∈{0，1}且使得qσ(f)≠-1，-2，…，-n，f(qz+η)≢f(z)。记

H2(z)=[P(f)(f(qz+η)-f(z))](k)，k∈

则以下结论成立。

(1) 若qs=1，m=1且a=α1，则0亦为H2(z)的Borel例外值，即H2(z)没有非零有穷Borel例外值。

(2) 若qs≠1或qs=1，m≠1，或qs=1，m=1，a≠α1，则H2(z)没有有穷Borel例外值。

(3)H2(z)取任意c∈{0}无穷多次，且满足λ(H2-c)=σ(f)。

2 定理1.1和定理1.2的证明

为证明定理1.1和定理1.2，我们需要以下两个引理。

引理2.1[11]设n∈+，P1(z)，P2(z)，…，Pn(z)是次数分别为d1，d2，…，dn的非常数多项式且满足当i≠j时，deg(Pi-Pj)=max{di，dj}。令

其中Bj(z)(≢0)，j=1，2，…，n为整函数且满足σ(Bj)

引理2.2[3]设n≥2，f1(z)，f2(z)，…，fn(z)为亚纯函数，g1(z)，g2(z)，…，gn(z)为整函数，且满足下列条件：

(2) 对于1≤j

(3) 对于1≤j≤n，1≤h

下面证明定理1.1和定理1.2。

定理1.1的证明因α1，α2，…，am为P(z)的不同零点，则P(f)可以表示

P(f)=an(f-α1)n1(f-α2)n2…(f-αm)nm

(2.1)

其中an≠0，n1+n2+…+nm=n。因f(z)为有穷正级超越整函数，且a为其有穷Borel例外值，故f(z)可以表示成

f(z)=a+g(z)eαzs

(2.2)

其中α(≠0)为复常数，s(≥1)为整数且满足σ(f)=s，g(z)(≢0)为整函数且满足σ(g)

f(qz+η)=a+g(qz+η)h(z)eqsαzs

(2.3)

其中h(z)(≢0)为整函数且满足σ(h)≤s-1。因此，由(2.1)～(2.3)式可得

ang(z)ng(qz+η)h(z)e(n+qs)αzs

(2.4)

P(f)f(qz+η)=ang(z)ng(qz+

η)h(z)e(n+qs)αzs

(2.5)

因qs≠-1，-2，…，-n，α≠2α≠…≠nα，qsα≠(1+qs)α≠…≠(n+qs)α，且g(z)h(z)≢0，σ(g)

(2.6)

其中βl=

情形1若仅存在一个βl0∈{α，2α，…，nα}∪{qsα，(1+qs)α，…，(n+qs)α}使得

H1(z)=gl0(z)eβl0zs

其中gl0(z)为(2.6)式中项eβl0zs的相应系数之和。显然，βl0≠0，gl0(z)≢0，σ(gl0)

情形2对其它情形，不失一般性，设

H1(z)=gl1(z)eβl1zs+gl2(z)eβl2zs+…+glr(z)eβlrzs

(2.7)

其中r∈{2，…，2n+1}，βl1，βl2，…，βlr∈{α，2α，…，nα}∪{qsα，(1+qs)α，…，(n+qs)α}

使得βli≠βlj(i≠j)，且gli(z)(≢0)，i=1，2，…，r满足σ(gli)

H1(z)=a*+g*(z)eβzs

(2.8)

其中β(≠0)为复常数，g*(z)(≢0)为整函数且满足σ(g*)

gl1(z)eβl1zs+…+glr(z)eβlrzs-g*(z)eβzs-a*=0

(2.9)

若β≠βlj，j=1，2，…，r，则由引理2.2和(2.9)式可得

gli(z)≡0，i=1，2，…，r，g*(z)≡0，a*≡0

矛盾。

若存在j∈{1，2，…，r}使得β=βlj，则(2.9)式可以表示成

(2.10)

由引理2.2和(2.10)式可得

glj(z)-g*(z)≡0，gli(z)≡0，i≠j，a*≡0

矛盾。因此，H1(z)没有有穷Borel例外值。

由情形1和情形2可知，H1(z)取任意c∈{0}无穷多次，且满足λ(H1-c)=σ(f)。

定理1.1证毕。

定理1.2的证明使用与定理1.1类似的证明方法，分以下四种情形进行证明。

情形1设qs=1，m=1，则由(2.1)～(2.3)式可得

(2.11)

又因为f(qz+η)≢f(z)，所以g(qz+η)h(z)≢g(z)，且由α≠2α≠…≠(n+1)α，g(z)h(z)≢0，σ(g)

H2(z)=h1(z)eαzs+h2(z)e2αzs+…+hn+1(z)e(n+1)αzs

(2.12)

其中hi(z)，i=1，2，…，n+1是关于g(z)，g(qz+η)，h(z)的微分多项式且满足σ(hi)

情形1.1当a=α1时，由(2.11)式和(2.12)式可得

H2(z)=hn+1(z)e(n+1)αzs

又由P(f)(f(qz+η)-f(z))≢0可知hn+1(z)≢0。因此，当qs=1，m=1，a=α1时，0为H2(z)的Borel例外值。

情形1.2当a≠α1时，记

则(2.11)式可以写成

P(f)(f(qz+η)-f(z))=A1(z)eαzs+A2(z)e2αzs+…+An+1(z)e(n+1)αzs

显然，Ai(z)≢0，σ(Ai)

使用与定理1.1中情形2类似的证明方法，易知当qs=1，m=1，a≠α1时，H2(z)没有有穷Borel例外值。

情形2设qs=1，m≠1，则

(2.13)

情形2.1若存在i∈{1，2，…，m}使得a=αi，不失一般性，设a=α1，则由(2.13)式可得

B1(z)e(n1+1)αzs+B2(z)e(n1+2)αzs+…+

Bn-n1+1(z)e(n+1)αzs

H2(z)=ht1(z)e(n1+1)αzs+ht2(z)e(n1+2)αzs+…+htn-n1+1(z)e(n+1)αzs

其中hti(z)，i=1，2，…，n-n1+1是关于g(z)，g(qz+η)，h(z)的微分多项式且满足σ(hti)

使用与定理1.1中情形2类似的证明方法，易知当qs=1，m≠1，且存在i∈{1，2，…，m}使得a=αi时，H2(z)没有有穷Borel例外值。

情形2.2若a≠αi，i=1，2，…，m，则由(2.13)式可得

使用与定理1.1中情形2类似的证明方法，易知当qs=1，m≠1，a≠αi，i=1，2，…，m时，H2(z)没有有穷Borel例外值。

情形3设qs≠1，m=1，则

P(f)(f(qz+η)-f(z))=an(a-α1+g(z)eαzs)n(g(qz+η)h(z)eqsαzs-g(z)eαzs)

(2.14)

情形3.1若a=α1，则由(2.14)式可得

P(f)(f(qz+η)-f(z))=ang(z)ng(qz+η)h(z)(n+qs)αzs-ang(z)n+1e(n+1)αzs

由qs≠-1，-2，…，-n，1，g(z)h(z)≢0，σ(g)

H2(z)=hv1(z)e(n+qs)αzs+hv2(z)e(n+1)αzs

其中hvi(z)，i=1，2是关于g(z)，g(qz+η)，h(z)的微分多项式且满足σ(hvi)

使用与定理1.1中情形2类似的证明方法，易知当qs≠1，m=1，a=α1时，H2(z)没有有穷Borel例外值。

情形3.2若a≠α1，则由(2.14)式可得

(2.15)

(a) 若qs-1不是整数，则iα≠(j+qs)α，i=1，2，…，n+1，j=0，1，…，n。由g(z)h(z)≢0，σ(g)

(b) 若qs-1是整数，因为qs-1≠0，-1，所以分以下两种情形进行证明。

若qs-1≥1，则对(2.15)式重排得到

P(f)(f(qz+η)-f(z))=-an(a-

α1)ng(z)eαzs+…+ang(z)ng(qz+

η)h(z)e(n+qs)αzs

由α≠(n+qs)α≠iα，i=2，3，…，n+1，α≠(n+qs)α≠(j+qs)α，j=0，1，…，n-1和g(z)h(z)≢0，σ(g)

若qs-1≤-2，则对(2.15)式重排得到

P(f)(f(qz+η)-f(z))=an(a-α1)ng(qz+η)h(z)eqsαzs+…-ang(z)n+1e(n+1)αzs

由qsα≠(n+1)α≠iα，i=1，2，…，n，qsα≠(n+1)α≠(j+qs)α，j=1，2，…，n和g(z)h(z)≢0，σ(g)

结合情形(a)和(b)，在(2.15)式中合并同类项，得到

使用与定理1.1中情形2类似的证明方法，易知当qs≠1，m=1，a≠α1时，H2(z)没有有穷Borel例外值。

情形4设qs≠1，m≠1，则

(2.16)

情形4.1若存在i∈{1，…，m}使得a=αi，不失一般性，设a=α1，则由(2.16)式可得

使用与情形3.2类似的证明方法，易知当qs≠1，m≠1，且存在i∈{1，…，m}使得a=αi时，H2(z)没有有穷Borel例外值。

情形4.2若a≠αi，i=1，2，…，m，则由(2.16)式可得

使用与情形3.2类似的证明方法，易知当qs≠1，m≠1，a≠αi，i=1，…，m时，H2(z)没有有穷Borel例外值。

由情形1～4可知，H2(z)取任意c∈{0}无穷多次，且满足λ(H2-c)=σ(f)。

定理1.2证毕。