基于分数阶模型的锂离子电池SOC与SOH协同估计

1 锂电池模型建立与参数辨识

1.1 模型建立

由于分数阶微积分在频域中建立的系统模型更加精确[3]，因此本文电池模型通过分数阶建立。为了不使模型过于复杂，难以实际应用，本文采用基于分数阶的二阶RC 等效电路模型，即使用两个恒相角元件CPE 替代整数阶模型中的电容，如图1 所示，其中UOCV为开路电压，R0表示内阻，R1、R2分别表示极化电阻和扩散电阻，CPE1、CPE2分别表示极化电容和扩散电容，U1、U2分别为极化电容和扩散电容的电压，I0为端电流，U0为端电压。

图1 分数阶等效电路模型

状态空间表达式如下：

式中：m、n分别是分数阶电容CPE1和CPE2的阶数；C1、C2分别是分数阶电容CPE1和CPE2的容量；SOC表示荷电状态，是关于t的函数；Qn是电池当前最大可用容量；UOCV(SOC)表示当前开路电压。

为了通过迭代计算估计电池状态，需要对式(1)做离散化处理。利用G-L(Grunwald-Letnikov)分数阶微积分定义处理分数阶的微分项，G-L 分数阶微积分定义为：

式中：α 为分数阶阶次；TS表示步长；t表示当前时刻；j表示步数。

分数阶二阶RC 电路模型的状态空间方程为：

1.2 模型参数辨识

模型参数的辨识是电池状态估计的基础[4]。自适应遗传算法(AGA)通过遗传参数自适应调整，提高了收敛精度与速度，因此本文采用AGA 辨识模型参数。

1.2.1 辨识内阻R0

辨识参数R0需要进行放电实验，本文采用的实验对象为10 个单体NCA 锂电池并联的电池包，并在成组前对各单体电池内阻和端电压进行测量，保证各单体电池间的一致性，主要参数如表1 所示。

表1 电池参数

在恒温箱中将电池环境温度设置为25 ℃，通过电子负载仪，将电池以0.5C充电至4.2 V，之后以4.2 V 充电至电流达到0.05C；静置2 h，标定此时满电，SOC=1；1C恒流放电3 min 后静置2 h，利用安时积分法得到并记录当前SOC下的OCV；循环上一步直至端电压小于2.5 V，并通过采集卡获取20 组不同SOC下的OCV数据。其中一个脉冲过程如图2所示。

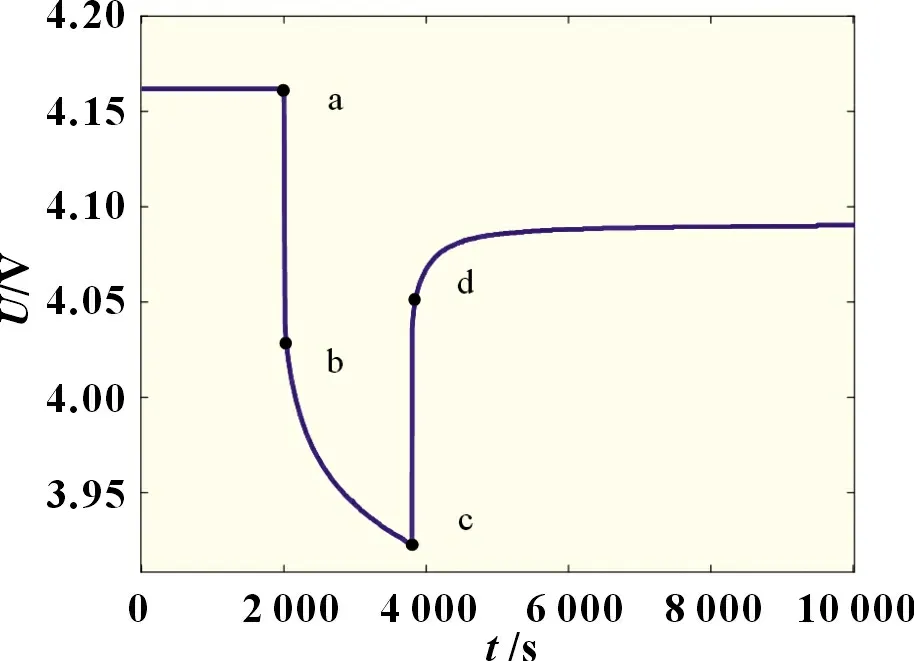
图2 脉冲放电电压曲线

由锂离子电池放电瞬间电压骤降的数据辨识内阻，计算方法为：

1.2.2 辨识参数R1、C1、R2、C2、m、n

AGA 辨识参数的收敛目标是测量电压与预测电压差值的平方和达到最小，而测量噪声等误差影响不可避免，因此本文设定当收敛度达到95%时满足收敛目标。利用AGA 得到分数阶和整数阶二阶RC 电路模型参数，如表2～表3所示。

表2 分数阶模型参数

表3 整数阶模型参数

利用上述放电实验数据和多项式拟合工具，得到UOCV(SOC)函数关系和SOC-OCV拟合曲线，如图3 所示。

图3 SOC-OCV拟合曲线

1.3 模型精度验证

PC 端向电子负载发送命令，通过电池模型恒流放电，利用采集卡获取实际端电压和分数阶模型、整数阶模型输出的端电压，并传送回PC端。端电压如图4所示，端电压误差如图5 所示，分数阶模型能更精确地跟踪实际端电压变化，分数阶模型的端电压误差更小，放电初期和末期误差相对较大的原因是锂离子电池在这两个时期内部化学结构不稳定[5]；整数阶模型的平均误差值和最大误差值为0.005 1 和0.055 1 V，分数阶模型的平均误差值和最大误差值为0.004 6 和0.033 5 V，分数阶模型的平均误差和最大误差都较小，且都小于整数阶模型。验证结果表明，本文采用的分数阶模型和参数辨识方法满足精度要求，为后续电池状态估计提供了保障。

图4 端电压曲线

图5 端电压误差曲线

2 电池状态估计

2.1 基于FOEKF 的SOC 估计

EKF 算法的核心是将非线性系统运用Taylor 方程展开，并利用KF 公式对系统进行状态估计的一种非线性递推方法[6]。EKF 通过对状态变量预测更新循环的过程，不断修正系统偏差，减弱外在干扰的影响，从而使估计得到的状态变量值更加接近真实情况。因此，结合式(3)所建立的状态空间方程，建立基于分数阶模型的扩展卡尔曼滤波器，其计算流程包括4 步。

(1)初始化x0、P0、Q0、R0。

(2)先验状态估计值和输出预测值：

当时间达到下一时刻k+2 时，从步骤(2)开始循环直至采样时间结束。

2.2 基于AUKF 的SOH 估计

AUKF 能够针对噪声特性进行实时动态更新，之后将更新后的噪声信息带入到UKF 算法[7]估计方程中，从而使估计精度更高。电池老化的一个重要指标是内阻的变化，因此，本文以R0作为状态变量估计电池SOH，两者间的关系可以表示为：

式中：RNEW表示内阻初始值；R0表示电池当前内阻。建立电池状态空间模型：

结合模型与AUKF 算法对电池SOH进行估计，计算流程包括5 步。

(1)初始化状态和协方差初始值：

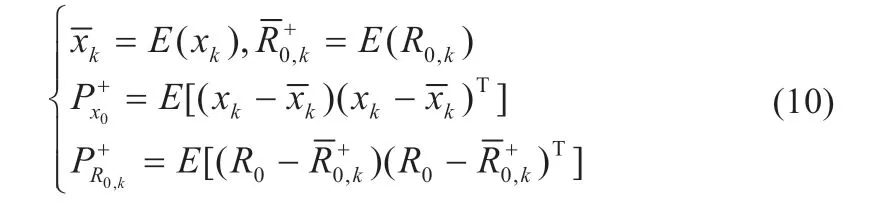
(2)计算采样点对应值：

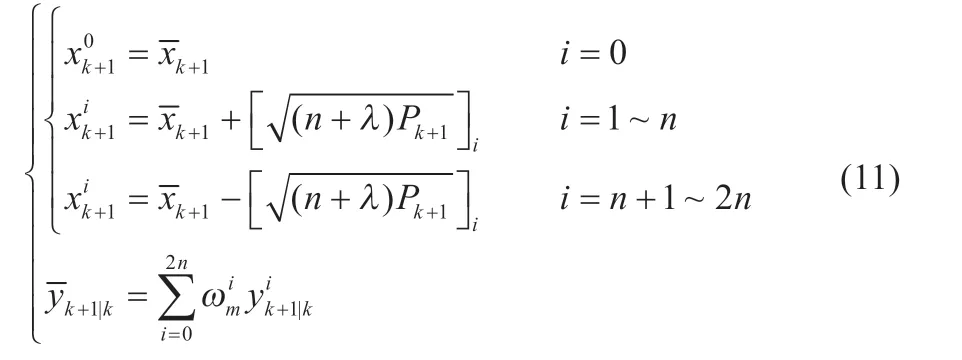
(3)时间更新：

(4)测量更新：

(5)过程噪声及测量噪声自适应匹配：

完成一步迭代后，根据当前估计结果更新均值、协方差以及过程噪声的统计特性，下一步迭代时重复执行上述过程，从而实现电池SOH的在线滚动估计。

2.3 基于FOEKF-AUKF的协同估计

结合上述算法，提出一种基于FOEKF-AUKF 的SOC、SOH协同估计算法。估计SOC时，将SOC作为唯一的状态变量，将R0视为常量；估计SOH时，将R0视为状态变量，将SOC视为常量，以此实现循环迭代计算，得到电池状态变量SOC和内阻在每个采样点的最优估计值，从而实现锂离子电池SOC、SOH的协同估计。总体步骤为：(1)模型参数初始化；(2)基于SOH估计的状态空间模型，利用AUKF 算法估计电池内阻R0；(3)基于SOC估计的状态空间模型，利用FOEKF 算法估计电池SOC；(4)根据步骤(2)中得到的内阻R0更新步骤(3)中FOEKF 迭代过程中的内阻参数，步骤(3)中得到的电池状态参数进一步修正步骤(2)中的模型参数，以此循环迭代。

3 实验验证

采用美国环境保护署(USEPA)制订的汽车国际通用城市道路循环工况(UDDS)实验[8]，UDDS 实验工况包含大小不同及周期不规律的工作电流，可以对电池状态估计算法进行验证。按比例缩小UDDS 工况得到实验所用的工况电流，如图6 所示。通过PC 端向电子负载发送命令，输入工况电流，对电池进行充放电，并利用采集卡记录数据送回PC 端。

图6 UDDS工况电流

3.1 SOC精度验证

考虑到实际条件下获取SOC初值时会存在误差，因此为更好地验证估计精度，将SOC初值设置为0.8，在UDDS 工况下，SOC真实值与采用FOEKF-AUKF、FOEKF、EKF 算法的SOC估计值如图7 所示，估计误差如图8 所示。实验结果表明，EKF 估计SOC的平均误差和最大误差分别为1.58%和2.86%；FOEKF 估计SOC的平均误差和最大误差分别为0.95%和2.01%；协同估计算法的SOC平均误差和最大误差分别为0.66%和1.54%。由于分数阶模型精度更高，且通过AUKF 实时更新噪声协方差和内阻R0，提高了对SOC估计的准确性和自适应性，因此该算法估计SOC的精度最高且收敛速度最快。

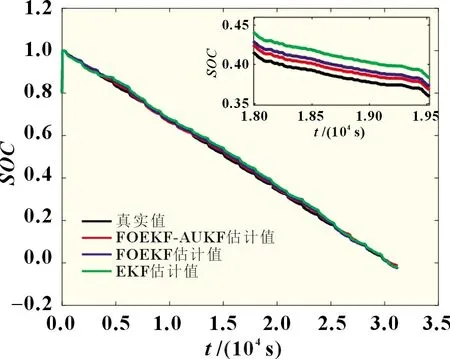
图7 SOC估计值

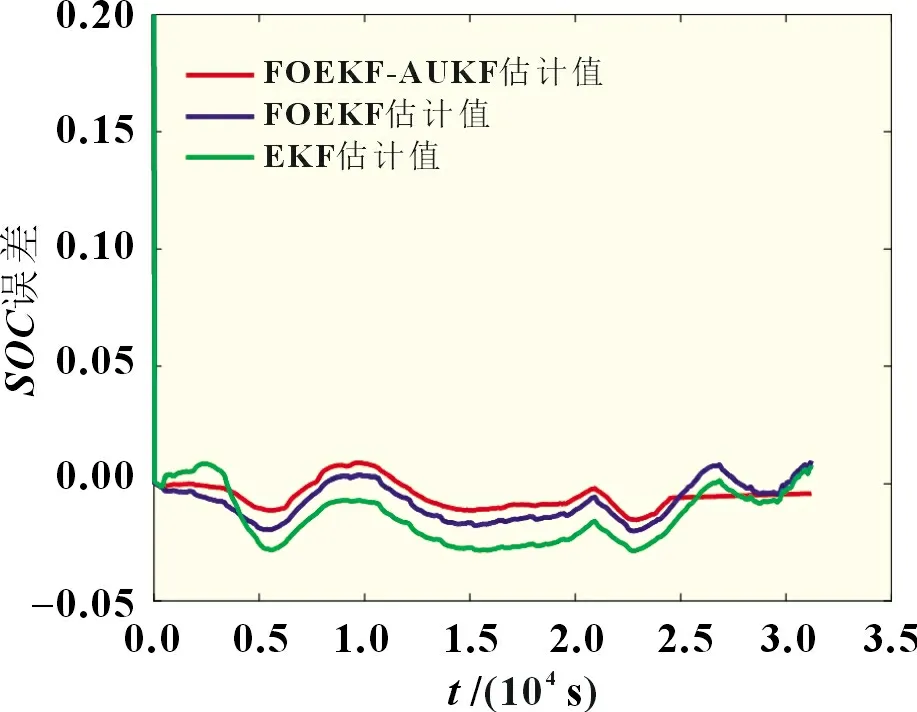
图8 SOC估计误差

3.2 SOH 精度验证

考虑到实验对象为全新电池，因此设置SOH初值为1，通过本文提出的协同估计算法估计出R0后，利用式(8)得到电池当前SOH，估计值与实际值如图9 所示。由图9 可知，通过误差协方差匹配，自适应过程噪声和测量噪声，估计的SOH与实测计算的SOH接近重合，误差小于1%。因此该算法能够较为精确地估计电池SOH。

图9 SOH估计值

4 结论

本文采用分数阶二阶RC 等效电路模型，并通过自适应遗传算法辨识模型参数，提出了一种FOEKF-AUKF 协同估计算法，对锂离子电池SOC和SOH进行估计。通过放电实验和工况实验，验证对比了模型精度和估计效果。实验结果表明，该算法估计SOC更加精确，收敛速度更快，估计SOH准确可靠且具有自适应性，误差小于1%；另外，两个滤波器共用信息，能够保证算法的稳定和收敛，为BMS 提供了一种可靠的状态估计方法。