题中悟道 模型备考
——2021年数学新高考全国Ⅰ卷数列解答题分析
>>>李 翠
数列是高中数学的重点内容,是考查考生逻辑推理和数学运算核心素养的重要载体。课程标准要求学生“探索并掌握等差数列、等比数列的通项公式与前n 项和的公式,能在具体问题情境中发现数列的等差关系或等比关系,并能用有关知识解决相应的问题”。纵观这几年高考数列解答题,难度中等,大稳定、小创新。本文以2021 年新高考全国Ⅰ卷数列解答题为例,分析考生存在的问题并提出备考建议。
一、原题再现

(1)记bn=a2n,写出b1,b2,并求数列{bn}的通项公式;
(2)求{an}的前20项和.
分析:第一问通过求特殊的两项b1,b2,再求数列{bn}的通项公式,降低了试题的难度,也体现出数列中从特殊到一般的推理方法;第二问,根据数列的特点进行分组求和,或者通过递推关系将奇数项转化为偶数项再求和。
解析:(1)由题设可得b1=a2=a1+1=2,b2=a4=a3+1=a2+2+1=5.
又a2k+2=a2k+1+1,a2k+1=a2k+2(k ∈N*).
故a2k+2=a2k+3,即bn+1=bn+3,即bn+1-bn=3.
所以{bn}是首项为2,公差为3 的等差数列,故bn=2+(n-1)×3=3n-1.
(2)方法一:设{an}的前20 项和为S20,则S20=a1+a2+a3+…+a20,
因为a1=a2-1,a3=a4-1,…,a19=a20-1,
所以S20=2(a2+a4+…+a18+a20)-10

方法二:由(1)知数列{an} 的奇数项与偶数项都是以3 为公差的等差数列.
设数列{an}的前20 项和为S20,则

二、考生存在的问题
从考生答题的情况看并不理想,仍然存在较大的问题,主要表现在以下几个方面。
1.对定义理解不准确
注重性质解题,不注重基本量运算,眼高手低。
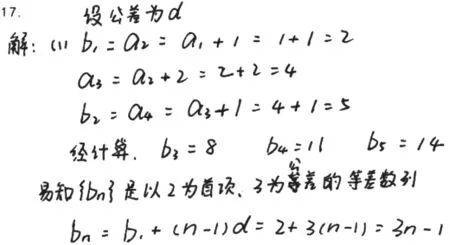
2.解题过程不规范,缺少必要的计算步骤和转化依据

3.逻辑推理的素养有待提升
不清楚求通项的关键在于通过递推关系寻找数列的特征、判断数列的类型,从而求出通项。

4.计算能力不高


三、备考建议
1.强化对数列定义、基础知识和基本方法的练习与巩固,用好教材。
2.熟练掌握等差数列、等比数列的通项公式和前n 项和公式,适当加强通过递推关系式和列举法观察规律的题目的训练。
3.加强新定义数列问题的研究,总结利用归纳猜想进一步求数列通项的解题规律。
4. 熟练掌握“累加法”“累乘法”“构造法”求数列的通项,“倒序相加法”“ 错位相减法”“ 裂项相消法”求数列前n 项和的解题方法,掌握利用递推关系求数列通项的题目特征及相应的求解方法。
5.数列解答题是容易得分的大题,主要考查数列的基本概念、基本量运算、基本方法的运用以及简单不等式的放缩等,建议在备考中加强常规方法的训练。

