小学数学思想方法渗透策略例谈

包敏

摘 要：数学思想方法是数学知识的精髓，教学中要充分运用教材中的素材有机渗透，要巧妙运用书本习题或改编习题筑牢所学数学思想，同时要引导学生运用数学思想方法寻找解决问题的策略。

关键词：小学数学;思想方法;课堂教学

数学思想方法是数学知识的精髓，《全日制义务教育数学课程标准（2011年版）》明确指出：“数学教学应根据具体的教学内容，注意从学生的实际出发，引导学生通过实践、思考、探索、交流等，获得数学的基础知识、基本技能、基本思想、基本活动经验，促使学生主动地、富有个性的学习。”[1]因此我们的日常教学不能只关注“双基”的教学，还应该有机渗透数学思想方法，同时让学生积累数学活动经验，下面我就结合教学案例谈谈自己在教学中有机渗透数学思想方法的一些基本策略。

小学数学思想方法是蕴藏在数学知识之中，在教材编排体系中它不是一个个完善的体系，也不是显性的教学内容，因此如何把握并有机渗透数学思想方法对教师来说非常重要，它关系到课程标准的要求是否有效落实，学生的能力是否得到培养等。目前在小学阶段所涉及到的数学思想方法有很多，常见的有：符号化思想、数形结合的思想、转化的思想、分类的思想、整体的思想和类比的思想、化归思想、集合思想、统计思想、极限思想等等。作为一名数学教师我在日常教学中比较重视数学思想的渗透，并从中摸索出几种有效的教学策略，与大家分享。

一、充分运用教材中的素材有机渗透数学思想

人教版的教材有着丰富的数学思想教学素材，作为一名教师，首先要认真解读教材，准确捕捉教材中的数学思想方法的内容，同时课前要精心设计教学方案，准确地将所要渗透的数学思想方法在教学中有机融合与渗透。比如：人教版一年级上册P17的“比大小”，书本中先呈现了3只猴子和一些随意摆放的水果，再将3只猴子与3种水果对应排列，用学生能接受的象形统计图呈现[2]。教学中我从引导学生读懂图意入手，让学生用心观察主题图，并与同桌交流你从图中读懂了什么，让学生在读懂图意的基础上明白“同样多”、“谁比谁多（少）”，近而再引导学生观察书本的象形统计图，渗透一一对应的思想。这样学生在经历了“观察、交流、思考、分析”的学习过程中不仅获得了“猴子与桃子的数量同样多”“猴子比香蕉多”“猴子比梨少”的信息，且初步感知了“一一对应”的数学思想。

再比如：在教学人教版三年级下册的两位数乘两位数的笔算乘法14×12的教学中，课本中给出了点子图，我在教学中充分利用“点子图”帮助学生理解算理，首先我让学生把自己的想法在点子图中圈一圈，再让学生将自己的想法在小组中交流，学生在圈的过程中出现多种计算方法有“14×4=56，56×3=168”;有“14×6=84，84×2=168”;有“14×10=140，14×2=28，140+28=168”等，这时我都给予充分肯定，肯定他们能运用“转化”的数学思想将新知转化为旧知，从而解决新的问题，学生在得到肯定的同时，再引导学生比较，这三种方法中哪种方法更好一些，并让学生说出理由，学生在交流中不但体会“先分后合”也就是把它拆成两位数乘一位数或两位数乘整十数的解决问题的策略，同时也有机渗透了“转化的思想和优化策略”，这样学生不仅学习了新的知识，同时又在潜移默化中巧妙地将有关的数学思想方法在教学中渗透。紧接着在竖式计算的教学环节中，我让学生结合点子图中的圈法来理解算理，进一步沟通算理与算法之间的联系，这时也就充分渗透了“数形结合思想”。

这样的例子教材中数不胜数，大家都知道在推导圆柱的表面积公式时，除了需要借助模型的思想，还需要让学生明白其中公式形式转化的意义。圆柱的表面积公式，我们在解释圆柱的表面积公式为什么可以写成，往往会利用乘法分配律来解释，但是这仅仅只是解释了公式的形式化表达，却忽略了公式背后所蕴含的转化思想和模型思想。在解决这个问题上我运用了转化的思想，将所求的问题圆柱的表面积进行无限分割重组，转化成一个近似的长方形。也就是将圆柱的两个底面无限分割成小的扇形，组合成一个小长方形，这个小长方形的长是，宽是。再将圆柱的侧面积展开成长是，宽是的小长方形。最后将两个小长方形拼成是，宽是的大长方形。这样就将公式的本质理清、说透，学生也能更好地理解和运用圓柱的表面积公式。

二、巧妙运用或改编教材中的习题筑牢数学思想

在教学中我除了充分利用教学中的素材有机渗透数学思想方法外，我还尝试运用书本的习题或改编习题来筑牢例题教学中对学生渗透的数学思想。当然，要做到这一点，教师要认真研究书本上的习题，理解编者的意图，在充分运用它。比如：在教学完“两位数乘两位数笔算乘法”（三年级下册）的例题后，我会让学生完成P47练习十中的第一题，再让学生利用点子图来梳理22×13的算理，这样不仅有利于学生对算理的理解，同时也让学生进一步体会“数形结合思想”在数学学习中的好处。此外我也会设计类似的练习让学生去巩固所学的知识同时筑牢相关的数学思想。比如：请你将下面的点子图圈一圈，表示出口算16×3的思考过程：“10×3=30，6×3=18，30+18=48”。

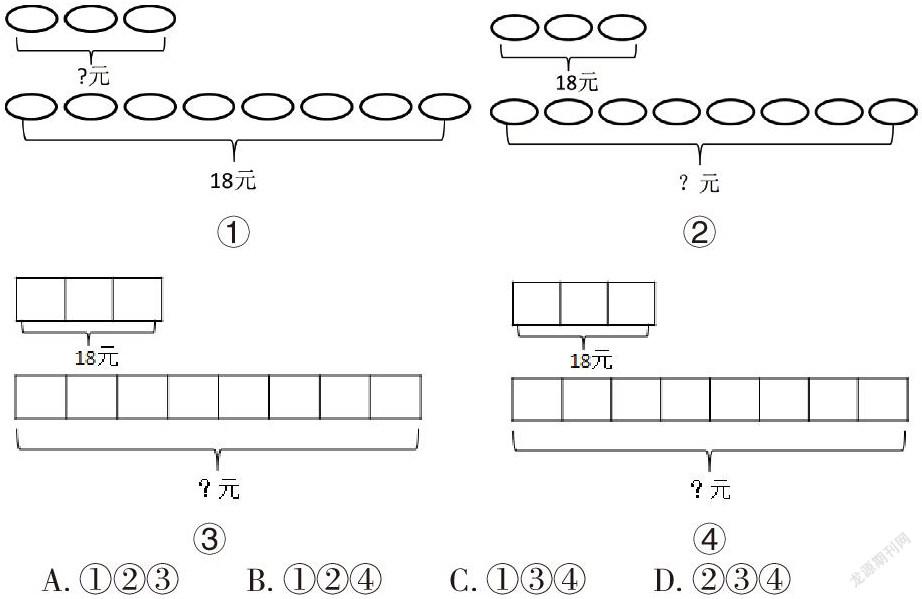
再比如：在三年级上册的P71例8（归一问题）的教学中[3]，我会在“阅读与理解”环节，鼓励学生用不同的方法呈现数学信息，学生在对比与交流中，体会到画示意图的方法简单明了，再让学生看书，借助书本的图进一步理解数量关系列出综合算式，从而解决问题。之后我会用例8这一素材改编习题如：下列能正确表示出“妈妈买3个碗用了18元，如果买8个同样的碗，需要多少钱？”的意思的图是（    ）。

A. ①②③  B. ①②④  C. ①③④  D.②③④

这样很好地巩固了所学的数学知识和这一例题折射出的“数形结合思想”。

三、适时引导学生运用数学思想解决问题

由于数学思想在小学数学中是“隐性”的知识，往往被学生甚至教师所忽略，但是数学思想方法对于提升学生的学科素养有着举足轻重的作用，就拿“数形结合的数学思想”来说它对于学生的学习就很重要。常言道：“数缺形时少直观，形少数时难入微”，如果能让学生自觉运用有关的数学思想来解决问题，那么学生的学习效率就提高了，学生的学科素养也是得到了培养，同时也为学生今后的学习打下了良好的基础。比如：“一个长方形的长去掉4厘米，面积比原来减少了20平方厘米，剩下的部分正好是一个正方形。这个长方形原来的面积是多少平方厘米？”在解决这个问题时，如果学生只是一味的看题或反复地读题，那么很难寻找到已知条件和问题之间的关系。但如果适时引导学生根据题意画图（如右图），数量关系就会一目了然，即：用20÷4=5（厘米），求出了长方形的宽，原长方形的面积就是（5+4）×5=45（平方厘米）。像这样的例子，在教学中还有很多，数形结合的思想在“解决问题”和“图形与几何”领域的教学中运用非常广泛。比如：数形结合思想在高年级的分数解决问题中更是常见，如果能适时引导学生用画线段图的方式找出分率与其对应的量，那么分数乘除法的应用题问题大都能迎刃而解，可见运用“数形结合”的思想不仅能更好地厘清题目中的数量关系，还能让学生形象直观地找到解决问题的突破口，从而顺利地解决数学问题。因此说数学思想方法的渗透表面上与传授知识无关，实际上运用合适的数学思想方法，有利于培养学生的数学学科素养，打开学生的解题思路，达到事半功倍的效果。

总之，在小学数学教学中要落实《课标》精神，重视“四基”教学，借助数学思想方法提高学生的学科素养，培养学生的高阶思维，让深度学习在教学中“落地”，切实让学生得到更好的发展。

参考文献：

[1].《全日制义务教育数学课程标准（2011年版）》

[2].《教师教学用书》（义务教育教科书 一年级上册）

[3].《教师教学用书》（义务教育教科书 三年级上册）