弱胶结砂岩在冲击荷载下的动力学性能研究

陈 波 孙利辉

（1.96781部队，陕西 宝鸡 721000；2.河北工程大学矿业与测绘工程学院，河北 邯郸 056038；3.北京科技大学土木与资源工程学院，北京 100083）

随着煤炭资源日益枯竭，其开采范围越发偏向于西部地区和地下深部。着眼于西部地区特殊的地质形态，在漫长地质历史时期内由该地区特有的层积环境而形成的特殊岩性（具有典型的弱胶结、易风化、塑性变形大、各向异性强、强度低等力学特性）的岩石［1］逐步成为研究的重点，对于其性能的研究也越来越多［2-5］。

煤岩体作为地层中广泛存在的一种材料，对其岩石静力学性能的探索，国内外学者早已做了大量的研究［6-11］。但在矿山开采过程中总离不开矿山的爆破、煤炭的运输、机械设备的运转等活动影响。这些活动与不可避免的地震运动等都可以看做是应力波对冲击矿压的诱发作用［12］，可以认为应力波伴随着整个采矿的开采过程［12-13］。冲击地压或爆破震动产生的能量继续对周围岩体产生往外扩散的应力波，从而导致更大范围内的破坏或者围岩松动。特别是岩石材料在冲击荷载下的动力学响应往往表现出与静荷载下的力学响应显著不同的特性［14-24］，单一的静载实验已经不能满足研究学者对于材料动态力学性能的研究需求。

大量的事实表明［25-26］，地质与开采的条件随着矿井的开采深度增加以及开采的难度加大而变的越来越复杂，强冲击矿压、塌方、冒顶、巷道的失稳等等在原始的地应力、构造应力、开采的扰动应力之间相互耦合作用下时常作为动力灾害发生，严重地影响了生产的安全和社会经济的发展

为此，选取内蒙古鄂尔多斯东胜煤田红庆河煤矿副井-680 m处所采集的延安组粉砂岩进行冲击荷载实验，旨在研究西部弱胶结粉砂岩在冲击荷载下所呈现出的动力学特性。

1 实验研究

实验设备主要是中国矿业大学的SHPB压杆实验装置，通过对所加工的弱胶结砂岩试样的冲击加载，研究冲击荷载下该类岩石所表现的动力学特征。

（1）SHPB实验装置由发射装置、入射杆、透射杆、吸收杆、缓冲器以及数据测量和记录系统组成。岩石试块置于输入杆与输出杆之间，入射杆、透射杆、子弹所用材料均为钢材，弹性模量为206 GPa，密度为7 800 kg/m3。应变片贴于入射杆与透射杆中间位置。本次实验采用400 mm子弹进行冲击实验，采样频率设置为8 000 kHz，采样长度为15K，采样延时设置为-2K。触发电平为0.312 5 V，触发方式选择为上升沿内触发。实验装置简图如图1所示。

1.1 实验方案

本实验选取4种加载能量，根据空气炮产生的压力，分别施加0.53 MPa、0.50 MPa、0.55 MPa、0.60 MPa 4种加载能量，每组选取3块试样进行，试样编号及分组如表1。根据“三波法”或“二波法”得出试样的全程动态应力—应变曲线，以及在不同加载作用下的力学参数，将动态抗压强度值与静态抗压强度值进行比较；对照组砂岩的动态强度与之相同加载速率下破坏的试样结果对照，总结出具有典型代表性的西部弱胶结砂岩的动静态力学强度及破坏特征。

1.2 实验原理

在中等应变率102～104s-1范围内，分离式霍普金森压杆（SHPB）是一种被普遍认可和广泛应用的测试技术。该实验的理论基础有2种：一是弹性杆中一维弹性波传输假设，二是试件的均匀变形假设。

如图2所示，当入射杆中入射脉波传播到试件界面时，一部分入射波—拉伸应力波的形式作为反射波发生反射，剩下的压缩波作为透射波通过试件传入输出杆（透射杆）继续传播，透射波形的幅值与长度取决于试样本身材料的性质。通过贴在入射杆和输出杆的超动态应变片测得入射杆和输出杆之间的应力波随时间变化的数值，从而直接测得入射波、反射波、透射波的应变值。

1.3 弱胶结砂岩的试样选取与制作

实验中选取内蒙古红庆河煤矿2#副井-680 m处常见的粉砂岩作为研究对象。现场选取的粉砂岩为侏罗系延安组二段的粉砂岩，呈灰色、深灰色的粉粒结构，内部为泥质胶结，显微波状层理或交错层理，呈条带状，含植物化石碎屑。

在进行静力学实验时，按照国际岩石力学学会ISRM推荐的实验方法，将试件打磨成ϕ50 mm×100 mm的标准试件。针对SHPB实验，参照相关文献［14］，将试样打磨成长径比为0.5的试样，即为ϕ50 mm×25 mm。经过取芯、切割、两端断面打磨的岩石试件，需保证其两端平行度和轴线垂直度均小于0.02 mm，使其符合规范要求。

1.4 弱胶结砂岩基本物理参数及力学参数的测定

1.4.1 物理参数的测定

实验中采用量积法测量其密度，采用非金属超声检测分析仪测量纵波波速。试样的基本物理参数如表2。

1.4.2 弱胶结岩石的力学参数

采用长春市朝阳仪器有限公司的GAW-2000型微机控制电液伺服刚性试验机，加载方式为控制位移的加载方式，加载速率为0.2 mm/min，应变率为3.3×10-5s-1。具体试样物理、力学参数见表3。根据实验数据做出应力—应变曲线，如图3。

从表3可以看出，岩石的单轴抗压强度的最小值为 33.69 MPa，最大值为 43.59 MPa，强度值在30～60 MPa之间，属于半坚硬岩石。

1.4.3 试样吸水性能

选取2块岩石试样进行泡水实验。将试样放在容器内加水至刚没过试样的表面，每隔12 h观察一次。在泡水12 h后第一次观察时试样就已经平行节理方向破裂，如图4。从图中不难看出该岩石吸水性较强，遇水易崩解。内部颗粒较细，多为泥质胶结，属于典型的西部地区弱胶结岩石。

2 实验数据分析

在实验之前应先对ϕ50 mm的SHPB实验系统进行标定，求得标定系数K=1.914 6×10-4。进行标定之后，找到应变—电压2种信号的换算关系，进而将测量得到的电压信号转化为应变信号，这样方可利用“二波法”或者“三波法”对实验数据进行处理，计算得到试样的应变率、应变、应力的数据，进一步得到试样的应力—应变曲线，从而可分析岩石的动态力学响应特征。

2.1 不同冲击荷载下的波形分析

根据标定系数将入射、反射、透射波形对应的电压值换算成相应的应变值，得到波形—时间的变化曲线即入射波、反射波、透射波与时间一一对应的曲线图，分别做出se1-4系列的三波图（图5～图8）。因se1-1数据的缺失，故在文中将此试样数据除去。

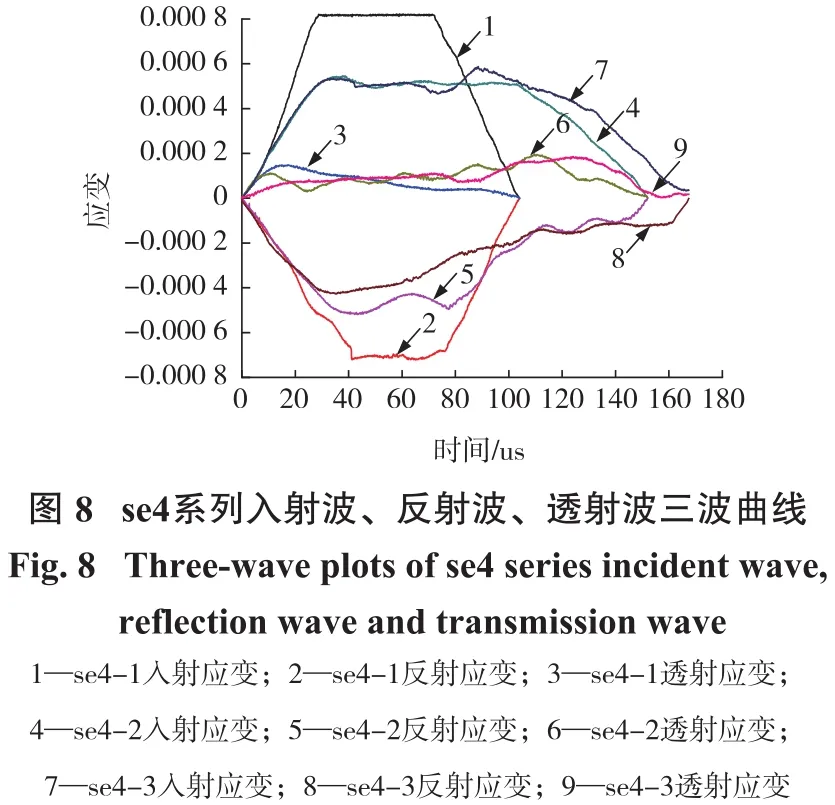
由图5～图8不难看出，se1系列的加载速度为5 m/s时的入射平台高度为0.000 6左右；se2系列由于加载速度较大，对应的平台高度也较高，平台的应变为0.000 8左右；se3系列中除了se3-3外，se3-1、se3-2的加载速度在7 m/s附近，相应的入射应变为0.000 7左右，介于se1系列与se2系列之间。由于se3-3的冲击速度接近于se1系列，为5.09 m/s，其相应的入射应变的平台高度也接近于se1系列，为0.000 58，数值上近似于0.000 6；同样对于se4系列，除了se4-1的加载速度靠近8 m/s的数值范围，其对应的应变平台也非常近似于se2系列的数值，其平台高度亦为0.000 81。对于se4-2和se4-3其加载的速度非常近似于se1系列，接近5 m/s，但是仍小于这个数值，故其入射平台的应变数值也稍低于se1中的2个系列的数值，均为0.000 52。根据相关数据做出岩石试样的子弹的撞击速度即加载速度与入射波平台应变的关系图表，如图9及表4所示。

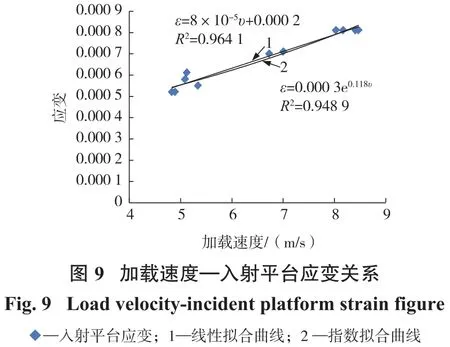
通过图9以及表4可知，随着加载速度的增加，入射波的平台应变也随之增加，入射波平台的应变值与加载速度之间的关系基本上可以用线性函数或者指数函数来拟合。当用指数函数来拟合时，拟合函数为ε=0.000 3e0.1181υ，其拟合度R²=0.95，相关系数R=0.97。用线性函数来拟合时，其拟合函数为ε=8× 10-5υ+0.000 2，拟合度为R²=0.96，相关系数R=0.98。可见相比于指数拟合，描述入射波平台的应变值与加载速度之间的关系时，线性函数具有更好的代表性。

通过表5及图10不难看出，应变率随加载速度的增加而变大。应变率与加载速度存在一定的线性或指数关系。其指数关系也可用指数函数来拟合，指数函数为=72.765e0.1158υ，拟合度R2=0.97，相关系数R=0.98；线性拟合关系的函数为=18.175υ+38.587，其拟合度为R2=0.97，相关系数R=0.98。对于应变率与加载速度关系的数据拟合，从拟合度上来说，二者非常相似，且接近与1，拟合度都比较好，故二者皆可用于描述弱胶结砂岩的应变率与加载速度的函数关系。

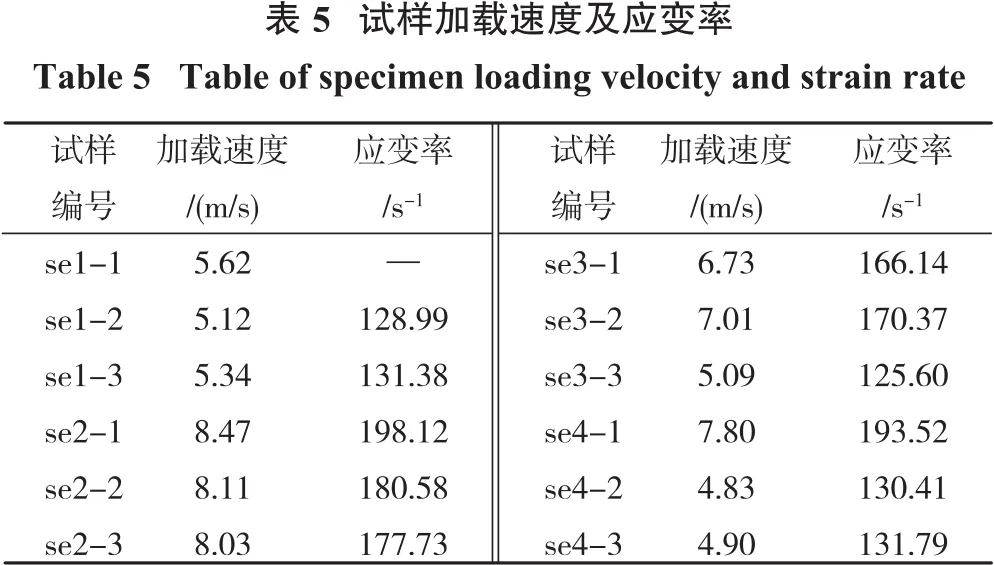
由上述分析可知，不仅仅在加载速度与入射波的平台应变之间存在着相关关系，应变率与加载速度之间也存在着一定的关系，故在应变率与入射波的平台应变之间势必会存在着一种内在的联系。为了确定应变率与入射波平台应变之间的关系，特将应变率为125.6 s-1、166.14 s-1、198.12 s-13种相差较大的应变率下的入射波、反射波、透射波，分别与对应时间关系的三波图以及单独的入射波图；应变率为分别125.6～131.79 s-1、166.14～198.12 s-1之间比较接近的入射波、反射波、透射波与时间关系的三波图以及入射平台应变与应变率之间的关系图绘制出来，如图11～图15。从图11～图15可以看出随着应变率的增加，入射波的平台应变也随之增加。针对二者之间所存在具体的关系，本文给出了二者之间3种不同的函数关系：指数函数、线性函数以及多项式函数。其中指数函数为ε=0.0003e0.0062ε.，拟合度为R2=0.89，相关系数R=0.94；线性函数为ε=4×10-6+2× 10-5，拟合度为R2=0.90，相关系数R=0.95；多项式函数为ε=5×10-93+2 × 10-62-4×10-4+0.0213，拟合度为R2=0.97，相关系数R=0.98。3种函数的拟合度都大于0.8，为高度拟合，但是根据拟合度的具体数值，三次多项式函数的R2值最大，其相比于另外两种函数的拟合度更好一些。

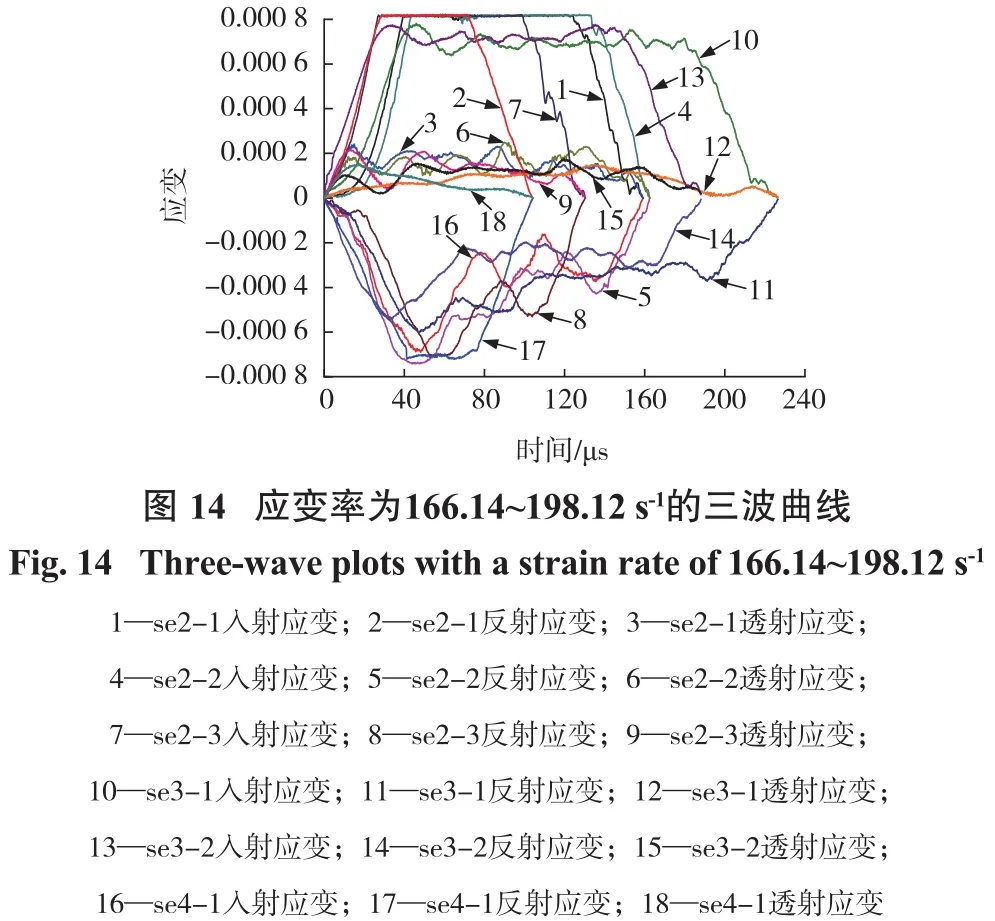
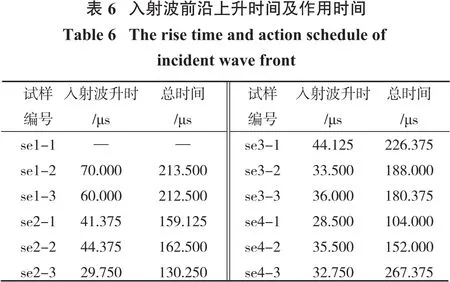
对应力波的作用时间和入射波的前沿上升时间而言，通过图5～图8、图11～图14以及表6可以看出除se4-1外，其他的冲击波的作用时间都大于150μs，满足试样达到应力平衡所需要的基本时间，且入射波的前沿上升时间都比较长，大部分位于30～40μs之间。对于加载速度较大的se2系列以及se4-1，其他试样的应力波的作用时间去掉se4-2这个偶然之值外，其余的时间均大于180 μs。文献［27，28］指出一个缓慢上升的入射脉冲，能够减少实验过程中的弥散效应和惯性效应，且要保证试样达到应变平衡，入射脉冲的作用时间一般为应力波在试样内传播时间的4～10倍，按照本实验所用弱胶结砂岩的试样，入射脉冲作用的时间应为22～73.5μs，从数值上来说，上述试样中加载应力波的作用时间均大于73.5μs，表明试样基本上均已在试样完全破坏前达到应力平衡状态。

2.2 不同冲击荷载下的强度特征分析

一般来说岩石的承载强度随加载速度的增加而提高，弱胶结砂岩也不例外。根据实验所得数据，分别做出来了se1系列～se4系列在不同冲击能量下的应力—应变图以及相应的试样破坏图（图16～图23）以及表7。不难看出应变率越大的试样，其峰值强度越大，破坏程度也越高。

从图16 se1系列的应力—应变关系中可以看出。不同于传统的静荷载的应力—应变曲线，应变率为130 s-1的弱胶结砂岩试样在应变较小时的应力就已经急剧上升25 MPa左右，接近该类岩石的静荷载下的单轴抗压强度（单轴抗压强度为33.69～43.56 MPa均值为39.08 MPa）的57%～74%，在高应变率下的弱胶结粉砂岩的强度能够接近其静载下单轴抗压强度。在接近单轴抗压强度的77%后，岩石试样在到达峰值应力前的应力随应变的增大上升的速度较加载初期有所减缓，当其达到峰值应力后，应力随应变的增加而急剧下降，岩石试样发生破坏。从图17其破坏程度上来看，应变率较大的se1-3较se1-2的破坏程度更高（试样se1-1进行冲击时数据丢失）。

从图18及图19可以看出，其应力—应变曲线呈现出“多峰”的状态，se2系列中3块试样破坏后基本上都成为碎颗粒状。对于se2系列的冲击实验，由于其加载速度均大于8 m/s，接近se1系列加载速度的1.6倍，岩石的应变率在此冲击荷载作用下会更高，岩石的破坏程度也更为严重。且相比于se1系列的应力—应变曲线，其在加载瞬间的应力就已经超过其单轴抗压强度，且有1个小的峰值，在小峰值后，应力先下降然后再缓慢上升，最后经过二或三次的上升下降，在达到最后一个峰值强度后，应力随应变增加急剧下降，试样最终丧失承载力，以比较碎的颗粒形式破坏。

se3系列中se3-1与se3-2的加载速度基本上在7 m/s左右，介于se1系列与se2系列，而且其峰值强度和应变率也介于两者之间。se3-2的加载速度稍大于se1系列，从其应力—应变曲线上来看，也接近于se1系列的曲线关系，从图20、图16及图18中不难看出，与se1系列和se2系列相比，se3系列中的3块试样在加载后应力急剧上升的斜率，介于se1系列与se2系列之间。纵观整个曲线的变化，其变化的规律基本上也接近于se1系列，应力都呈现先急剧上升，然后再保持平稳上升，最后在峰值应力后，迅速丧失承载力，发生破坏。其破坏后的碎块的粒径从直观上看较se1系列的要小，较se2系列的要大些。从表7不难看出，3块试样之间的峰值强度也基本上随应变率增加而增加，se3-3加载速度最小，为5.489 m/s。相应的应变率也最小，为125.6 s-1，其对应的峰值强度48.17 MPa也是三者中的最小值。se3-2的加载速度最大，对应的应变率和峰值强度也是最大值。

参照se1系列、se2系列、se3系列的分析，se4系列中除se4-1试样外se4-2与se4-3的加载速度均小于5 m/s，接近se1系列的加载速度，故其峰值强度和应变率非常接近于se1系列（见表7）。从图22可以看出其应力—应变曲线接近se1系列的曲线关系。稍有不同的是，由于se4-2与se4-3的加载速度略低于se1系列加载速度，其应变急剧上升后的应力—应变曲线更加趋于平稳。se4-1的加载速度与se2系列非常接近，其应变率与峰值强度也接近于se2系列。但同se2系列的应力—应变曲线存在很大的区别。从图22中可以看出se4-1的应力—应变为单峰曲线，加载初期应力急剧上升至峰值后，应力随应变下降，在此后一段时间内仍有一定的承载力。对比图18中应力—应变曲线关系，se4-1与se2-3相似，与se2-2、se2-3的区别在于se2-1、se2-2均在应力急剧上升后略有下降再缓慢上升之后达到峰值强度，在峰值后迅速丧失承载能力。se4-1与se2-3加载初就已达到峰值应力，且峰值后的一段时间内其承载能力仍然存在，最后达到一定的损伤后，试样破坏。

综合以上对se各系列的分析结果不难看出，冲击荷载下的该类弱胶结粉砂岩的强度较其单轴抗压强度具有大幅度的提升。且基本上在应力波作用初期，应力就已经能够达到其静荷载时的峰值强度。此后应力—应变才开始缓慢上升，最后达到峰值强度。除se2-3、se4-1之外，其余试样在峰值强度后基本上很快丧失其承载能力。冲击的速度越大，冲击能量越高，试样的应变率也就越大，对应的峰值强度也就越高。故按照应力上升的速率不同基本上可以将其高应变率下的应力—应变曲线大致分成3个阶段：应力骤升阶段、应力—应变平缓上升阶段、应力陡然下降阶段。在应力骤升阶段中，在应变很小的时候，应力就可以快速上升甚至超过试样的单轴抗压强度。在此阶段中，随着压缩波在试样内部的急剧传播，在冲击后入射杆上的应力波快速传播到与试样接触的界面后发生反射与透射，透射的压缩应力波在试样内短暂而急剧传播，造成试样在小应变下的高应力。本研究认为在此阶段内试样内部的颗粒在短时间内承受较大的力的作用时，由于其内部胶结物较小，且多为粘性矿物，在短暂冲击荷载下，其内部空隙能够瞬间缩小凝聚，承载力有很大的提高。在应力达到一定值时，进入应力—应变平缓上升阶段，其内部的空隙基本上被粘性胶结物充填，试样体积缩小，颗粒之间靠颗粒本身和胶结物开始共同承载，应力—应变基本上呈平稳增长状态，逐渐达到其承载极限，到达峰值应力；在峰值应力后，试样很快进入到应力陡然下降阶段，此时经过应力波来回压缩损伤后的试样内部胶结物之间的粘结基本上不复存在，颗粒本身也基本上丧失其承载力，试样此时已完全丧失承载力，应力迅速下降，试样破坏。对于se2-3和se4-1所表现出的不同状态，本研究认为二者与se2-1、se2-2的“多峰”应力曲线的原因基本一致，因为此4块试样的应变率都非常高，基本上都在180 s-1以上，在如此高的应变率下，试样内部颗粒和颗粒之间的胶结呈现出更强的“硬化”性能，在试样完全“硬化”之前，应力波的快速传播使得应力到达第一次的峰值。在第一次峰值后，材料在高应变率下继续硬化，但此时传播过来的应力波经衰减后，对更加硬化的试样所造成的应力有短暂的降低或保持其现有的应力水平，应变继续增加。当材料完全“高度硬化”后，试样内部开始共同承载，弱胶结砂岩此时经过多次应力波传播造成的损伤后，应变增加较小的情况下，短暂的应力—应变平稳增长到达峰值。经过峰值强度后，材料开始丧失其承载力。由于其硬化程度非常高，在丧失承载力的过程中也并不像其他几块试样迅速，相比之下，其峰后的应力下降坡度也相之较缓。

根据表7的数据做出不同应变率下的峰值强度曲线和动弹性模量曲线图，如图24～图25。前面已经指出应变率与试样的峰值强度存在一定的关系，故针对应变率在128.993～198.12 s-1内与峰值强度和动弹性模量的关系，均选用了2种常用的数学模型：指数函数和线性函数。对于峰值强度和应变率之间的指数关系拟合函数为，其拟合相似度R2=0.89，相关系数R=0.94；其线性关系拟合函数为σ=0.454 9+8.309 4，拟合相似度R2=0.89，相关系数R=0.94。对于动弹性模量与应变率之间的关系，其指数拟合函数为Ed=1.415e0.0124ε。，拟合相似度R2=0.83，相关系数R=0.91；其线性关系拟合函数为Ed=0.135 2-10.661，拟合相似度R2=0.81，相关系数R=0.90。无论是应变率与峰值强度的函数拟合，还是应变率与动弹性模量之间的函数拟合，从拟合度上来说，2种函数关系的拟合度均大于0.8，且非常接近，属于高度拟合。综合前面的分析，笔者更倾向于用指数函数描述该类岩石应变率与其动荷载强度的关系。因为通过本次实验可以看出弱胶结砂岩在高应变率下会产生“硬化”现象，当应变率高于一定值时，其“硬化”的效果不是单一的与应变率呈现线性关系，而更像是一种指数增长型的“硬化模式”。此类粉砂岩的“应变率效应”非常明显，在受到冲击荷载时强度不仅能提高，而且提高值也非常大，最大提高值为49.94 MPa，为单轴抗压均值的1.28，且与应变率之间存在很好的指数增长关系。

文献［21］中选取的为中部地区长湘高速的砂岩，其单轴抗压强度为109.55 MPa，其动静强度比在应变率140 s-1时达到最大为1.8。文献［22］中选取的为中部地区长沙县采石场砂岩，其单轴抗压强度为126.37 MPa，动态强度为176.30 MPa。文献［23］中选取的河南能源化工集团车集煤矿2611工作面内的粉砂岩，其单轴抗压强度为90.18 MPa，动态强度最大为536.43 MPa、最小为214.58 MPa。尽管本研究中的砂岩动态强度相比其单轴抗压强度提升很高，最大动、静强度比为2.14，最大值为83.63 MPa，其动荷载下的最大强度都不能达到中部地区砂岩静荷载的强度。可见相比于中东部地区的砂岩岩性，尽管西部地区弱胶结的砂岩强度能够在冲击荷载下有所提升，但其提高后的强度仍不能达到中东部的砂岩强度。在冲击荷载作用下，弱胶结砂岩亦很容易发生破坏。

3 结 论

（1）通过对其波形、强度特征2个方面对弱胶结的粉砂岩的分析，得出其动态响应特征。应力波在弱胶结砂岩试样内的传播，基本上能够在试样破坏前达到内部应力平衡。入射波平台高度与冲击荷载大小有关，冲击速度越大，平台的高度也越高，相近的冲击速度下的平台高度值也相近。

（2）弱胶结砂岩在高冲击荷载下具有极强的“应变率效应”。由于其本身强度较低（均值39.08 MPa），在高应变率下的强度往往能够提高数倍，最大值为83.63 MPa，为单轴抗压强度的2.14倍，强度提高1.14倍。高应变率下的峰值强度随应变率的增加而提高，应变率越高，峰值越大，试样破碎的程度也越高。二者呈“指数”增长或“线性增长”的关系。其应力—应变曲线按照应力的增速大致分为3个阶段；应力骤升阶段、应力—应变平缓上升阶段、应力陡然下降阶段。在更高应变率下更容易出现“多峰”的应力—应变曲线。岩石的强度较静态抗压实验的强度值有较大的提高。不能以单一的静态抗压强度作为其在动态破坏下的强度指标。