双钢板混凝土组合板抗爆性能分析*

赵春风，何凯城，卢 欣，潘 蓉，王静峰,3，李晓杰

（1.合肥工业大学土木与水利工程学院，安徽 合肥 230009；2.大连理工大学工业装备与分析国家重点实验室，辽宁 大连 116024；3.合肥工业大学安徽先进钢结构技术与产业化协同创新中心，安徽 合肥 230009；4.生态环境部核与辐射安全中心，北京 100082）

钢板混凝土剪力墙是一种新型抗侧力构件，通过连接件将钢板与混凝土耦合，充分发挥钢材抗拉和混凝土抗压的性能，将两者的优势相结合，使结构具有较高的刚度和承载能力，特别适合用于抵抗冲击和爆炸等偶然荷载。钢板混凝土剪力墙具有高延性和高耗能能力，已应用于高层建筑、桥梁结构、核反应堆安全壳、海洋平台以及储油罐等结构[1-6]。

近年来，工业气体爆炸和恐怖爆炸袭击时有发生，造成建筑物严重破坏和人们生命财产巨大损失。例如，2018年7月10日美国威斯康辛州天然气爆炸事故，2019年3月21日江苏响水特大爆炸事故，2020年8月4日黎巴嫩贝鲁特港口爆炸事故等，都使当地建筑物遭受严重破坏。墙板是整个建筑物中的主要受力构件，在各类爆炸事故和袭击中极易受到爆炸荷载的冲击破坏，其抗爆性能事关整个建筑物的整体安全性。钢板混凝土剪力墙板作为一种新型的结构构件，其抗爆性能仍未得到充分重视和研究。因此，开展钢板混凝土墙板在爆炸荷载作用下的动态响应和抗爆性能，对于提高建筑物抗爆能力，提升结构的整体安全性，具有十分重要的工程意义和研究价值。

目前，对于钢筋混凝土板的抗爆性能已经进行了一定研究，而对双钢板混凝土剪力墙板的抗爆性能研究极少。Zhao等[7-9]进行了普通钢筋混凝土板和60°配筋混凝土板的爆炸实验，提出了基于比例距离、几何尺寸和边界条件的ORC和NRC板的爆炸挠度的拟合公式。赵春风等[10]研究了接触爆炸作用下单侧钢板混凝土组合板和夹芯钢板混凝土组合板的动态响应、破坏模式和抗爆性能。结果表明夹芯钢板混凝土组合板连接性和整体性较好，跨中挠度较小，具备继续承载的能力。汪维等[11]研究了POZD涂层方形钢筋混凝土板在接触爆炸作用下的破坏模式和抗爆性能，结果表明POZD涂层可以改善钢筋混凝土板的抗爆性能。Yan等[12]研究了弧形钢板剪力墙的抗冲击性能，结果表明混凝土核心是耗能的主要部分，其次是顶部钢板和底部钢板。针对钢板剪力墙的研究主要集中于抗震性能，很少针对钢板混凝土剪力墙结构抗爆性能。

本文中，对接触爆炸作用下钢筋混凝土板(reinforced concrete slab,RCS)和双钢板混凝土板(steelconcrete-steel composite slab,SCS)的动态响应和抗爆性能开展实验研究，对比钢筋混凝土板和双钢板混凝土组合板的破坏效果及其抗爆能力。参数化分析炸药量、混凝土强度和钢板厚度等参数对双钢板混凝土板抗爆性能的影响规律，利用多参数非线性回归分析方法，提出双钢混凝土板跨中挠度的预测公式。

1 实验概况

根据GJB/T 380–2015《钢板剪力墙技术规程》[13]规定和室外爆炸场地要求，采用缩尺比1∶4进行几何缩尺。试件原型为一个4 m×4 m×0.3 m的墙体，钢板尺寸、栓钉直径等几何尺寸均按照1∶4进行缩放，分别制作了钢筋混凝土板（RCS）和双钢板混凝土板(SCS)试件，并进行正常养护。采用人工振捣方式浇筑混凝土，得到3个150 mm×150 mm×150 mm的混凝土立方体试件，由抗压实验获得3个试件的抗压强度分别为30.2、30.9和31.4 MPa，平均立方体抗压强度为30.8 MPa，换算成轴心抗压强度为20.6 MPa。

钢筋混凝土板和钢-混凝土-钢混凝土组合板几何尺寸均为1 000 mm×1 000 mm×75 mm：HRB335级钢筋单层双向配筋，钢筋直径6 mm，间距75 mm，混凝土为C30，混凝土保护层厚度30 mm；钢板厚度3 mm，混凝土为C25，采用焊钉加螺帽的形式代替栓钉，栓钉直径3 mm，焊钉长度25 mm。钢筋混凝土板和双侧钢板混凝土板结构形式及尺寸如图1～2所示，试件材料力学性能见表1。

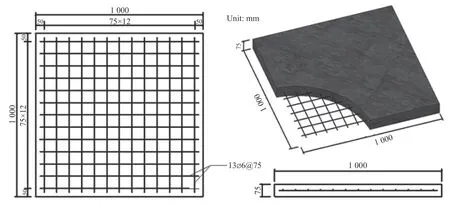
图1 RCS的几何尺寸及配筋方式Fig.1 Dimensions of RCS and reinforcement layout

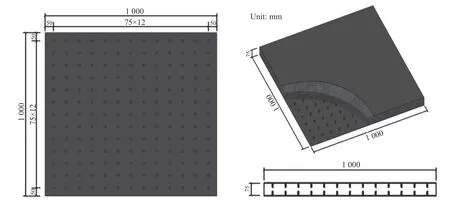
图2 SCS的几何尺寸和结构形式Fig.2 Dimensions and structural style of SCS

表1 材料力学性能参数Table1 Mechanical properties of materials

制作了支撑和固定混凝土板的钢框架，混凝土板一对边为固定约束，另一对边为自由。使用G型夹近似固支的方法将实验板对边固定在钢框架上，采用线起爆方式引爆放置于板面中心的炸药，实验装置布置如图3所示。

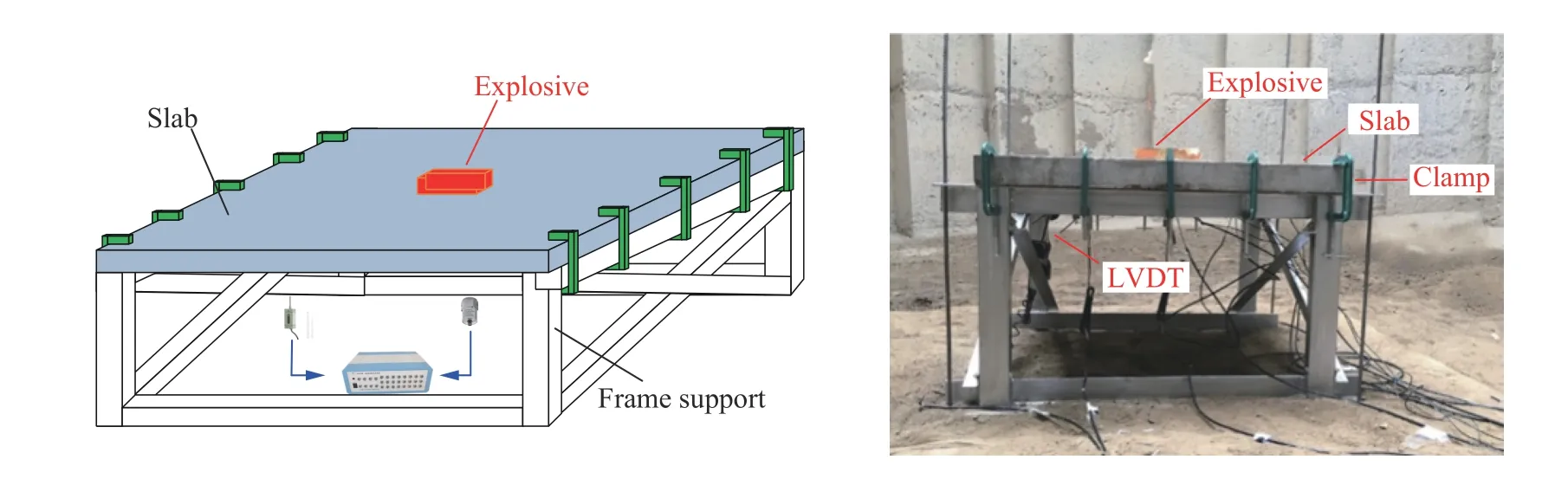
图3 实验装置Fig.3 Experimental setup

采用量程为±50 mm的位移传感器、100 Hz的动态采集仪和频率范围0.5～2 000 Hz的加速度传感器等，进行数据采集。实验板下表面布置3个位移传感器D1、D2和D3，3个加速度传感器A1、A2和A3。由于接触爆炸实验易造成试件跨中混凝土冲切破坏，因此位移计和加速度计布置在炸药放置点周围，测点布置如图4所示。

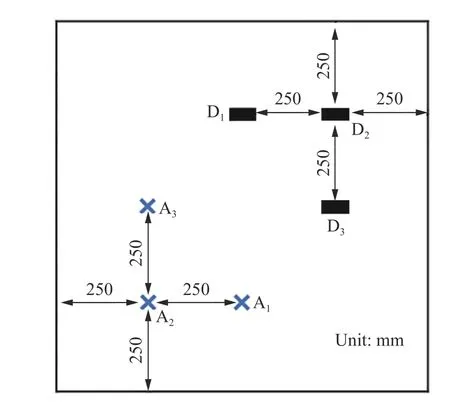
图4 测点布置Fig.4 Arrangement of measure points

2 数值模型

2.1 有限元模型及收敛性分析

利用ANSYS/LS-DYNA软件完成实体建模、材料定义、接触定义、网格划分以及边界条件定义。考虑构件和荷载的对称性，同时为了减少计算量，建立四分之一模型，如图5所示。选用共节点分离式模型，混凝土、空气和炸药采用solid单元，钢筋和栓钉采用link单元，钢板采用shell单元。采用400 g乳化炸药，按照0.7的换算系数相当于280 g TNT炸药当量，建模时采用高能炸药材料模型，密度为1.63 t/m3，按四分之一建模时折算的炸药尺寸为35 mm×35 mm×35 mm。采用自动面面接触算法（*CONTACT_AUTOMATIC_SURFACE_TO_SURFACE）模拟钢板与混凝土之间的作用。由于爆炸持续时间极短，栓钉和混凝土之间的相对滑移可以忽略不计，因此采用共节点方法实现两者之间的相互作用。同时，通过添加关键字*MAT_ADD_EROSION控制混凝土单元失效[10]。

有限元网格分别取2.5、5.0、10和15 mm，计算实验钢筋混凝土板跨中节点位移，得到位移曲线如图6所示。网格尺寸为2.5、5.0、10和15 mm时，对应的跨中节点峰值位移分别为48.5、47.5、48.3和46.2 mm，相对于网格尺寸2.5 mm时的误差分别为0、2%、0.4%和4.7%，网格尺寸取为10 mm时既具有较高的精度又占用计算机内存较小，同时与实验跨中节点位移50 mm的误差仅为3.4%，所以网格尺寸取10 mm。

2.2 材料模型

2.2.1 混凝土

混凝土采用*CONCRETE_DAMAGE_Rel3[14-15]材料模型，该模型考虑损伤和应变率的影响，用于模拟混凝土在爆炸冲击荷载作用下的受力性能，应用较为广泛。可以通过给定混凝土无约束抗压强度、混凝土材料密度和泊松比自动生成模型其余参数。抗压强度fcu,k=30MPa ，密度 ρ=2.4g/cm3，泊松比ν=0.19。

在爆炸荷载作用下，混凝土的抗压和抗拉强度受应变率的影响而得到一定程度的提高，引入动力增大系数 α[15]来考虑应变率效应， α 表示在某个应变率下材料动力强度与静力强度的比值。其中，混凝土抗压强度动力增大系数 αc为[16]：

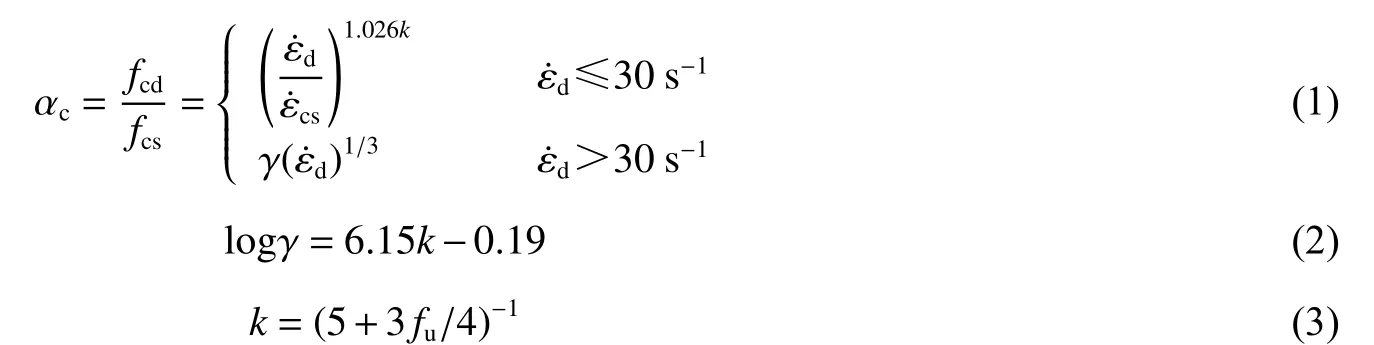
式 中：fcd为 混 凝 土 应 变 率 为ε˙d时 的 动 力 抗 压 强 度；fcs为 混 凝 土 应 变 率 为ε˙cs时 的 静 力 抗 压 强 度，ε˙cs=30×10−6s−1；fu为静载下混凝土立方体抗压强度。

混凝土抗拉强度动力增大系数 αt为[16]：

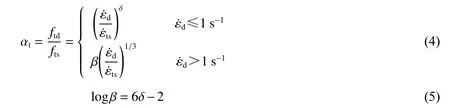
式中：ftd为混凝土应变率为 ε˙d时的动力抗拉强度；fts为 混凝土应变率为 ε ˙cs时的静力抗拉强度， ε ˙ts=10−6s−1；为静载下混凝土单轴抗拉强度，=10MPa 。

2.2.2 钢筋及栓钉

钢筋和栓钉采用随动硬化模型*MAT_PLASTIC_KINEMATIC[14]。钢筋和栓钉的应变率效应可通过Cowper-Symonds模型定义，该模型自带失效设置，强化后的钢筋和栓钉屈服应力为：

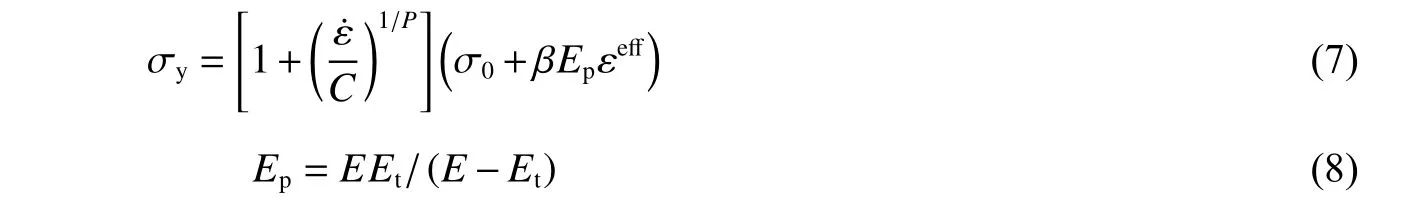
式中： ε˙ 为应变率， σ0为初始屈服应力， β 为硬化参数， εeff为有效塑性应变，C、P为Cowper-Symonds模型的应变率参数，Ep为塑性硬化参量，Et为切线弹性模量，E为初始弹性模量。

2.2.3 钢板

钢板采用Johnson-Cook（JC）模型和Grüneisen状态方程描述。Grüneisen状态方程定义压缩材料压力为：

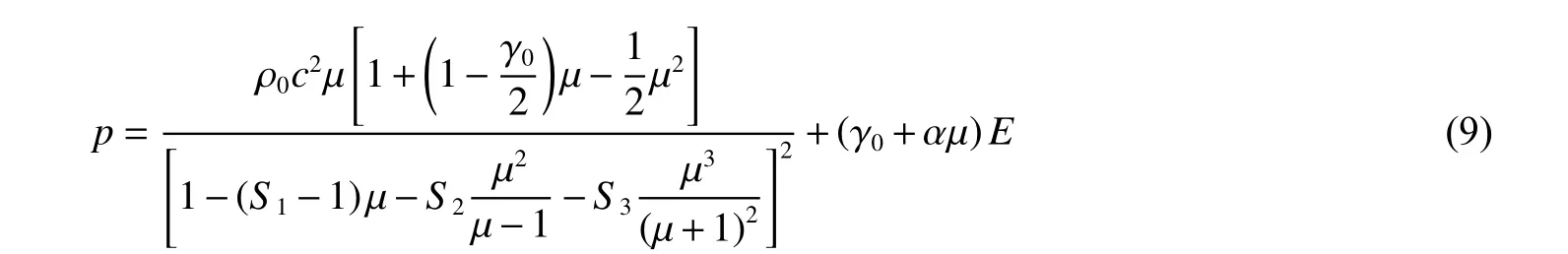
式中：c为vs-vp曲线的截距（速度单位），S1、S2和S3为vs-vp曲线斜率的系数，γ0是Grüneisen常数，µ=ρ/ρ0−1 ，α为γ0的一阶体积修正。

2.2.4 空气及炸药

将空气视作无黏性理想气体，其状态方程用NULL模型和LINEAR_POLYNOMIAL多项式表示：

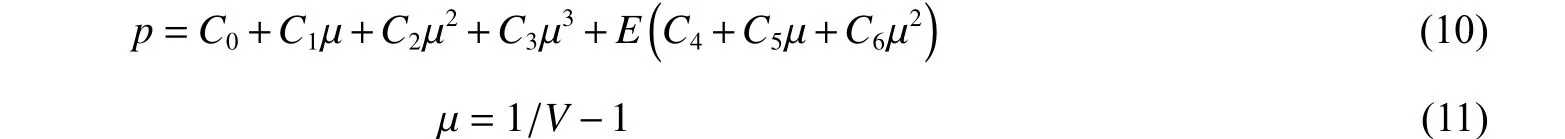
式中：p为气体压力，E为体积内能，V为相对体积。

炸药采用高速爆燃材料模型和JWL状态方程描述：

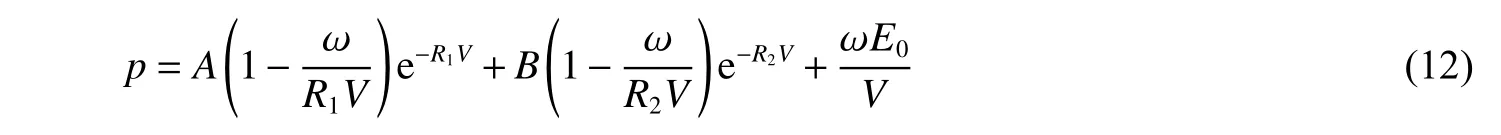
式中：p为爆轰压力；V为相对体积；E0为初始体积内能，E0=8.0GPa；A=540.9GPa，B=9.4GPa ，R1=4.5 ，R2=1.1， ω =0.35 。

3 实验与数值结果

3.1 钢筋混凝土板（RCS）

3.1.1 实验

图7为接触爆炸作用下钢筋混凝土板实验破坏现象图。RCS试件中心装药处发生贯穿，因混凝土的抗拉强度远低于其抗压强度，中心混凝土发生冲切破坏，钢筋裸露，迎爆面爆坑尺寸为360 mm×300 mm，背爆面震塌坑尺寸为410 mm×400 mm。平行自由边方向的爆坑直径大于平行于约束对边方向的爆坑直径，其原因与实验采用的条形炸药有关。RCS试件迎爆面爆坑周围有多条径向压缩裂缝，背爆面出现多条径向拉伸裂缝，裂缝由爆坑向四周发散，同时迎爆面与背爆面径向裂缝周围均产生多条放射状小裂纹。

图7 RCS试件破坏的实验结果Fig.7 Experimental results of RCS damage

3.1.2 数值模拟

图8为爆炸荷载作用下数值模拟与实验的损伤模式对比图。实验中混凝土块冲切脱落，同时爆坑中钢筋裸露。数值模拟中RCS试件中心发生贯穿，洞口周围混凝土单元虽未失效，但与周围混凝土单元已脱离连接。迎爆面爆坑尺寸为300 mm×300 mm，与实验相差16.7%，背爆面震塌坑尺寸为380 mm×360 mm，与实验相差16.6%，数值模型能较合理地模拟钢筋混凝土板的破坏情况。造成数值模拟结果和实验结果差异的原因可能是：数值模型采用了理想的材料模型，实验试件的混凝土材料具有很大的离散性和不均匀性；数值模拟采用了理想的固定约束条件，实验采用了一种近似固支的约束条件。同时，由于炸药爆炸产生的空气冲击波三维分布不均衡，实验结果会受炸药类型及形状、起爆条件、实际起爆点位置和炸药靶板相对位置等的影响，而数值模拟仍采用了理想的起爆方式及炸药靶板相对位置，所以数值模拟与实验结果有差异。与实验现象相同，数值模拟结果显示迎爆面和背爆面均出现了不同程度的径向裂缝，背爆面裂缝数量明显多于迎爆面。这是由于背爆面受拉伸波作用，迎爆面受压缩波作用，而混凝土抗拉强度远小于抗压强度，所以背爆面裂缝多于迎爆面。

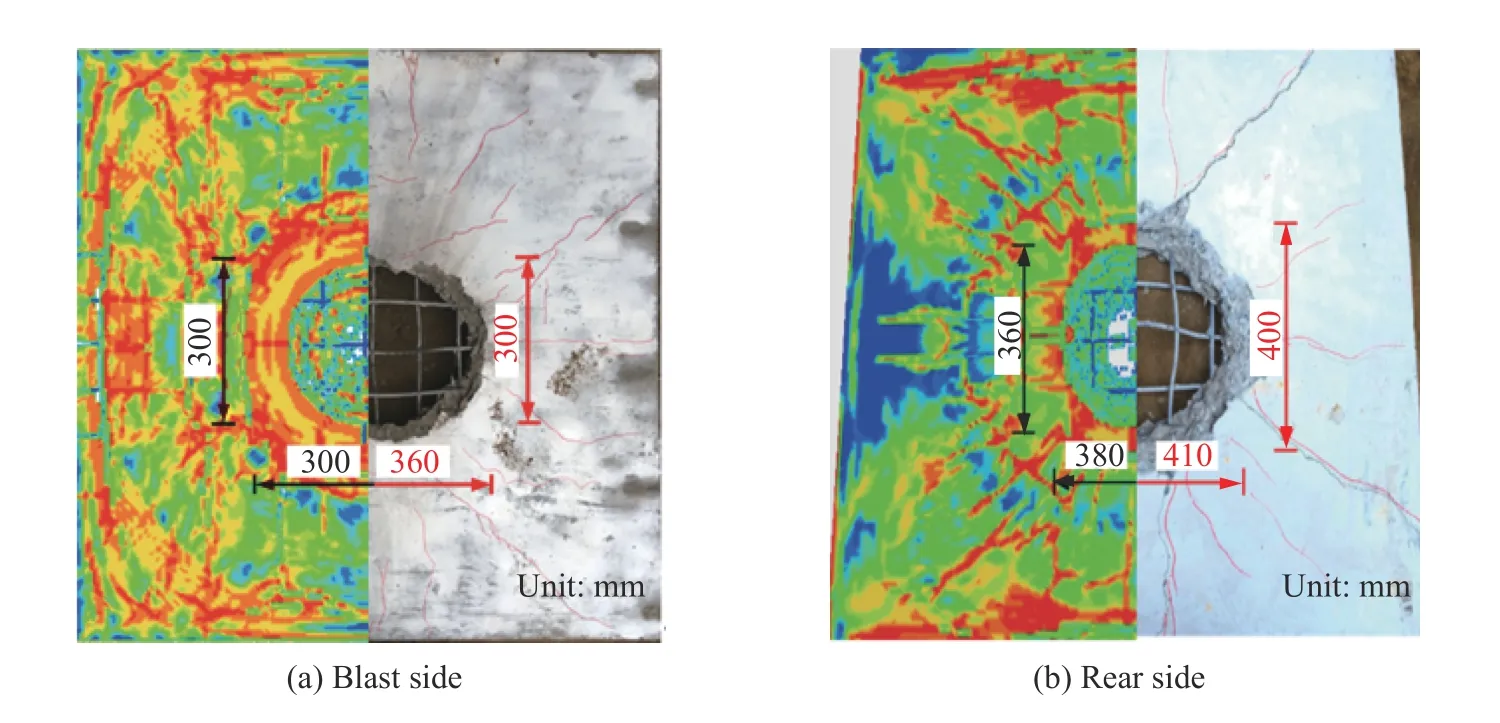
图8 RCS试件破坏的实验和数值模拟结果Fig.8 Experimental and numerical results of RCS damages

图9为爆炸作用下RCS试件的钢筋挠曲变形图。在爆炸波的作用下，钢筋发生发生严重的挠曲变形。实验测量得到的钢筋的最大挠度如图10所示，考虑钢筋直径和混凝土保护层厚度的影响，挠度为50 mm。数值模拟得到的跨中钢筋挠度为48.3 mm，与实验相差3.4%，数值结果与实验结果误差较小，表明数值模型能有效模拟钢筋的变形情况。

图9 RCS试件钢筋变形的实验和数值模拟结果Fig.9 Experimental and numerical results of RCS’s rebar deformation

图10 RCS试件钢筋的最大挠度Fig.10 Maximum deflection of RCS’s rebar

3.1.3 位移与加速度

图11为RCS试件不同测点的位移曲线。由于采集仪频率较低，在2 ms内仅得到两个测点，但实验得到的位移曲线整体趋势与数值计算结果基本吻合。图12为RCS试件测点加速度曲线，在2 ms内测得两个测点，第2测点的加速度分别为47.5、55.0和45.0 mm/ms2。数值计算的加速度曲线反映了实验板在爆炸荷载作用下的动态响应，结果表明数值结果测点位移和加速度趋势与实验结果相近，略有下降。这是由于数值分析时实验和模拟采用的约束方式有差别，同时数值模型采用的理想材料模型不能完全模拟实验模型材料的不均匀性和离散性。

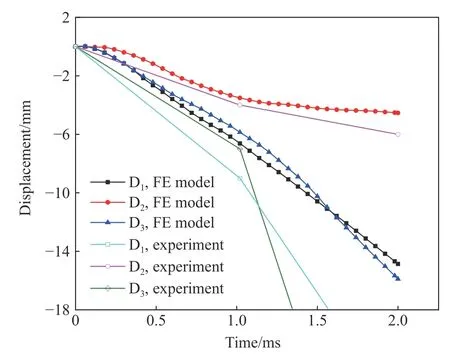
图11 RCS试件测点的位移曲线Fig.11 Displacement curves of RCS

图12 RCS试件测点的加速度曲线Fig.12 Acceleration curves of RCS

3.2 钢-混凝土-钢组合板（SCS）

3.2.1 实验

图13为钢-混凝土-钢组合板试件迎爆面和背爆面的破坏图。SRS相对于RCS整体性较好，在接触爆炸荷载下仍具有较好的完整性，具有继续承受荷载的能力。迎爆面爆坑尺寸为280 mm×180 mm，爆坑中间钢板受冲击波作用发生塑性损伤。背爆面钢板产生大面积盘形凸起，钢板非固支边跨中产生挠曲变形。核心混凝土在爆坑范围内发生压碎，但由于两侧钢板的存在未产生飞溅破坏，核心混凝土跨中产生纵向贯穿裂缝。迎爆面钢板爆坑范围内栓钉被剪断，钢板表面相应位置发生塑性破坏。迎爆侧钢板与混凝土之间未发生明显脱离，但背爆面钢板与核心混凝土发生脱离，栓钉被拔出，如图14所示。SCS跨中挠度如图15所示。

图13 SCS试件破坏的实验结果Fig.13 Experimental results of SCS damage

图15 SCS试件钢板的跨中挠度Fig.15 Deflection in midspan of SCS’s steel plate

3.2.2 数值模拟

图16为钢-混凝土-钢组合板试件的有效塑性应变的数值与实验对比图。迎爆面侧钢板爆坑尺寸为200 mm×200 mm，与实验的280 mm×180 mm误差10.7%，同时爆坑内钢板发生塑性破坏，与实验现象相符。背爆面侧钢板出现盘形凸起，与实验现象一致。混凝土跨中大部分已经发生破坏，爆坑周围环状裂缝清晰，同时由爆坑四周产生4条延伸向试件四角的大裂缝，平行试件固支边也出现两条清晰的裂缝，自由边跨中产生4条贯穿裂缝。图17为SCS试件核心混凝土数值分析结果，由于拉伸波作用，背爆面钢板栓钉出现拔出现象，钢板与混凝土发生部分分离，与实验结果类似。由于两侧钢板的包裹作用，混凝土破坏部分未脱落，整体性较好。实验测量SCS试件背爆面钢板跨中挠度为35 mm，数值分析结果与实验结果误差21.7%。

图16 SCS试件破坏的实验和数值模拟结果Fig.16 Experimental and numerical results of SCS damages

图17 SCS试件核心混凝土的数值模拟结果Fig.17 Numerical results of SCS’s concrete core

3.2.3 位移和加速度

图18～19分别为数值分析结果的测点位移曲线和加速度曲线，SCS试件钢板测点的位移曲线同RCS试件测点的位移曲线趋势大致相似，测点位移在前600 µs左右几乎保持不变，直到波峰到达才产生位移，并随时间逐渐平缓。数值测点位移和加速度与实验结果相近，但数值分析得到的测点位移偏低，而峰值加速度却偏高，这与实验中采集仪频率较低有关。

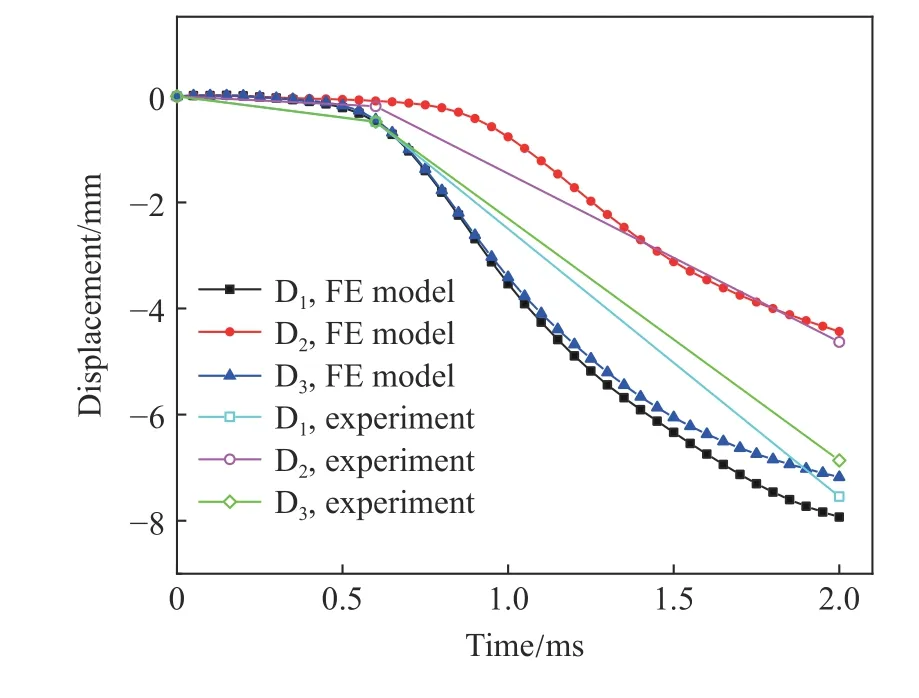
图 18 SCS试件测点的位移曲线Fig.18 Displacement curves of SCS

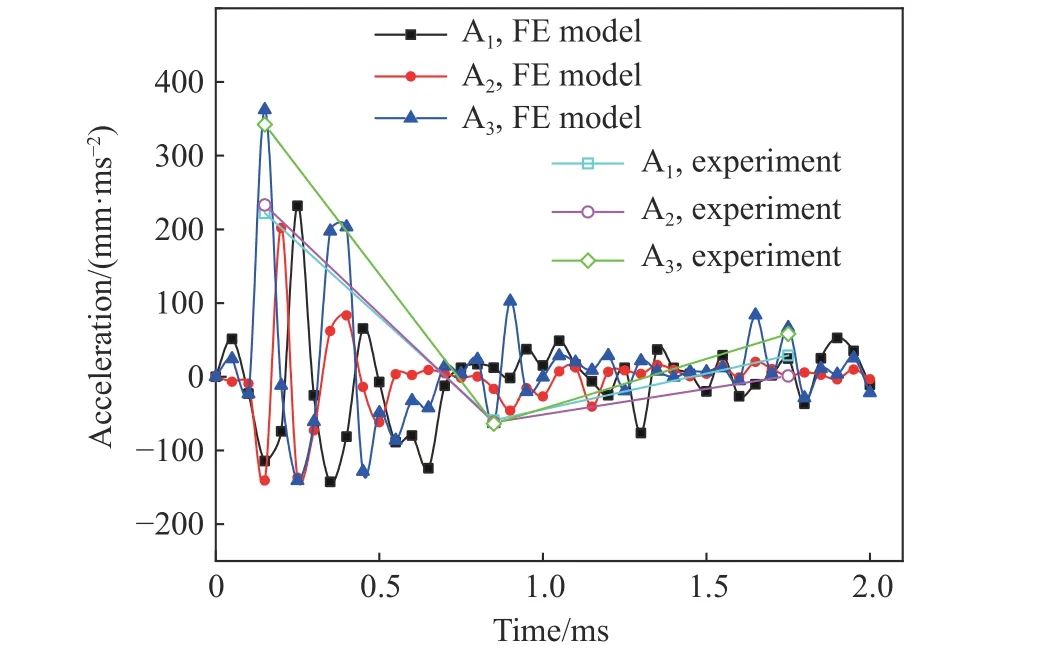
图19 SCS试件测点的加速度曲线Fig.19 Acceleration curves of SCS

3.3 SCS试件与RCS试件对比

表2为RCS和SCS试件的混凝土塑性损伤面积和挠度对比。相对于RCS试件，SCS试件迎爆面破坏尺寸有明显减小，实验迎爆面损伤面积减小53.3%，数值迎爆面减小55.6%。其原因可能是混凝土抗拉强度较小，整体发生冲切破坏。SCS试件背爆面未产生爆坑，而是在底部钢板产生了盘形凸起。SCS试件两侧设置了钢板，由于钢板的约束作用，核心混凝土碎块无剥落，不会产生混凝土飞溅，同时混凝土降低了两侧钢板的屈曲变形，底部钢板无损伤破坏，保持较好的整体性，仍具有承载能力。

表2 试件的损伤和挠度Table2 Damages and deflections of specimens

4 钢-混凝土-钢组合板（SCS）参数分析

为了了解药量、混凝土等级和钢板厚度3个参数对钢-混凝土-钢组合板抗爆性能的影响，选取跨中最大挠度作为钢-混凝土-钢组合板抗爆能力的关键指标进行对比，验证其抵抗变形的能力。

4.1 药量

炸药量分别为100、150、200、250和300 g，其余参数均保持不变，分析不同药量下组合板的爆炸响应。图20为不同药量下钢-混凝土-钢组合板中混凝土的有效塑性应变。当药量为100、150、200和250 g时，塑性变形量逐渐增大，但迎爆面钢板未发生破坏；当药量增加到300 g时，迎爆面钢板发生塑性损伤。不同药量下，混凝土跨中均发生了贯穿破坏。随着药量增加，背爆面径向裂纹和环形裂纹不断增多，同时4个角点都有不同程度的破坏。图21为组合板跨中位移曲线，当药量分别为100、150、200、250、300 g时，对应的跨中最大位移分别为10.90、12.08、14.88、15.05和27.15 mm，随着药量的增大，钢-混凝土-钢组合板板底挠度逐渐增加。而由图22可知，跨钢板跨中最大位移与药量呈非线性关系。

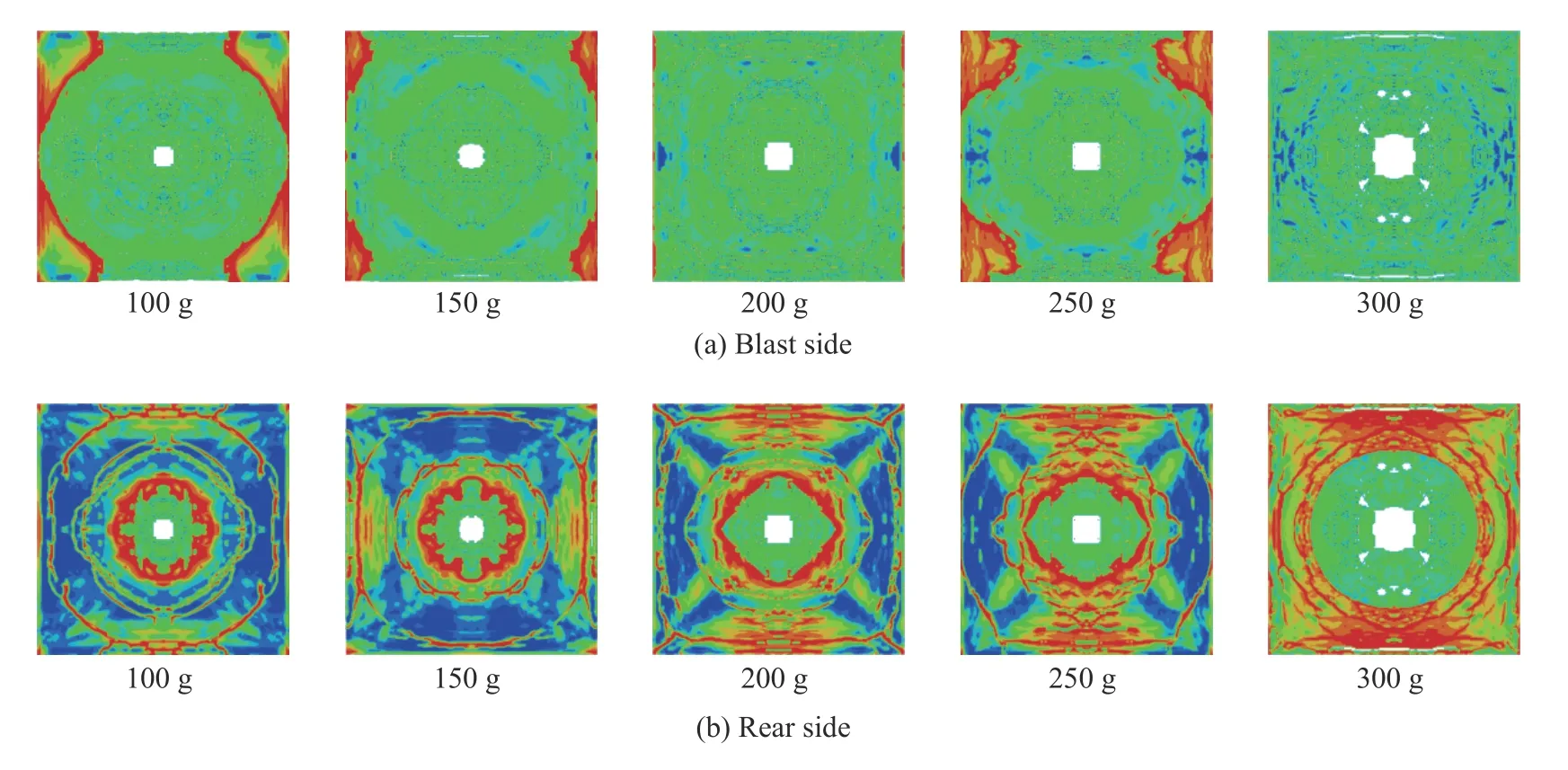
图20 不同炸药量时SCS中混凝土的有效塑性应变Fig.20 Effective plastic strains of concrete in SCS with different explosive charges

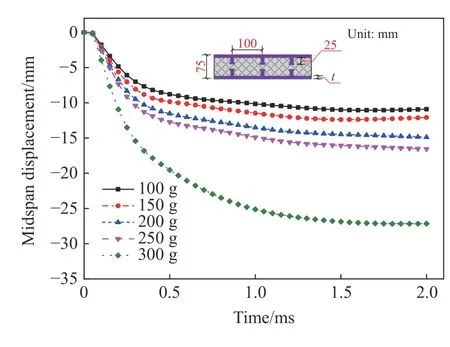
图21 不同炸药量时SCS的跨中位移曲线Fig.21 Mid-span displacement curves of SCS with different explosive charges

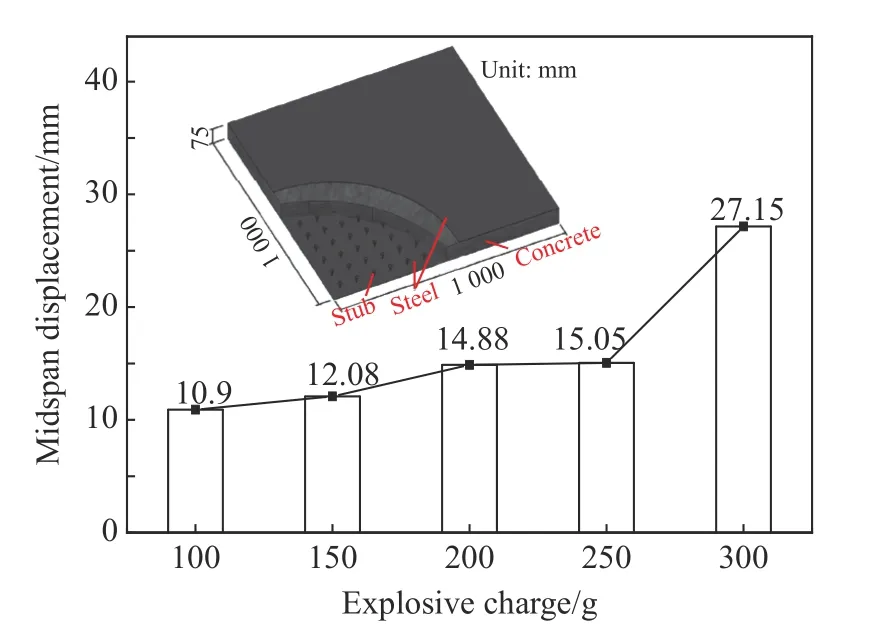
图22 不同炸药量时SCS的跨中最大位移Fig.22 Maximum displacements of SCS with different explosive charges

4.2 混凝土强度

混凝土分别为C30、C35、C40、C45和C50，其余参数均保持不变，分析不同混凝土强度下组合板的爆炸响应。图23为不同混凝土抗压强度下钢-混凝土-钢组合板中混凝土的有效塑性应变。当混凝土为C30时，夹心混凝土迎爆面及背爆面均产生大面积塑性损伤，混凝土迎爆面靠近自由边的区域也发生了塑性破坏，混凝土背爆面爆坑外侧存在多条环形裂缝。随着混凝土强度提高，混凝土迎爆面及背爆面塑性损伤区域逐渐减小，但当混凝土为C50时，两侧仍有较大的塑性损伤面积。图24为组合板跨中位移曲线，混凝土为C30、C35、C40、C45和C50时，对应的板底跨中最大位移分别为27.59、27.09、27.15、26.34和27.13 mm。由图25可见，当混凝土强度增加时，板底跨中最大位移呈波动变化，但变化不大。这是因为，钢-混凝土-钢组合板抗爆性能主要受钢板部分的影响，钢板吸收的大部分爆炸能量，所以，提高混凝土强度并不能显著改善组合板的抗爆性能。

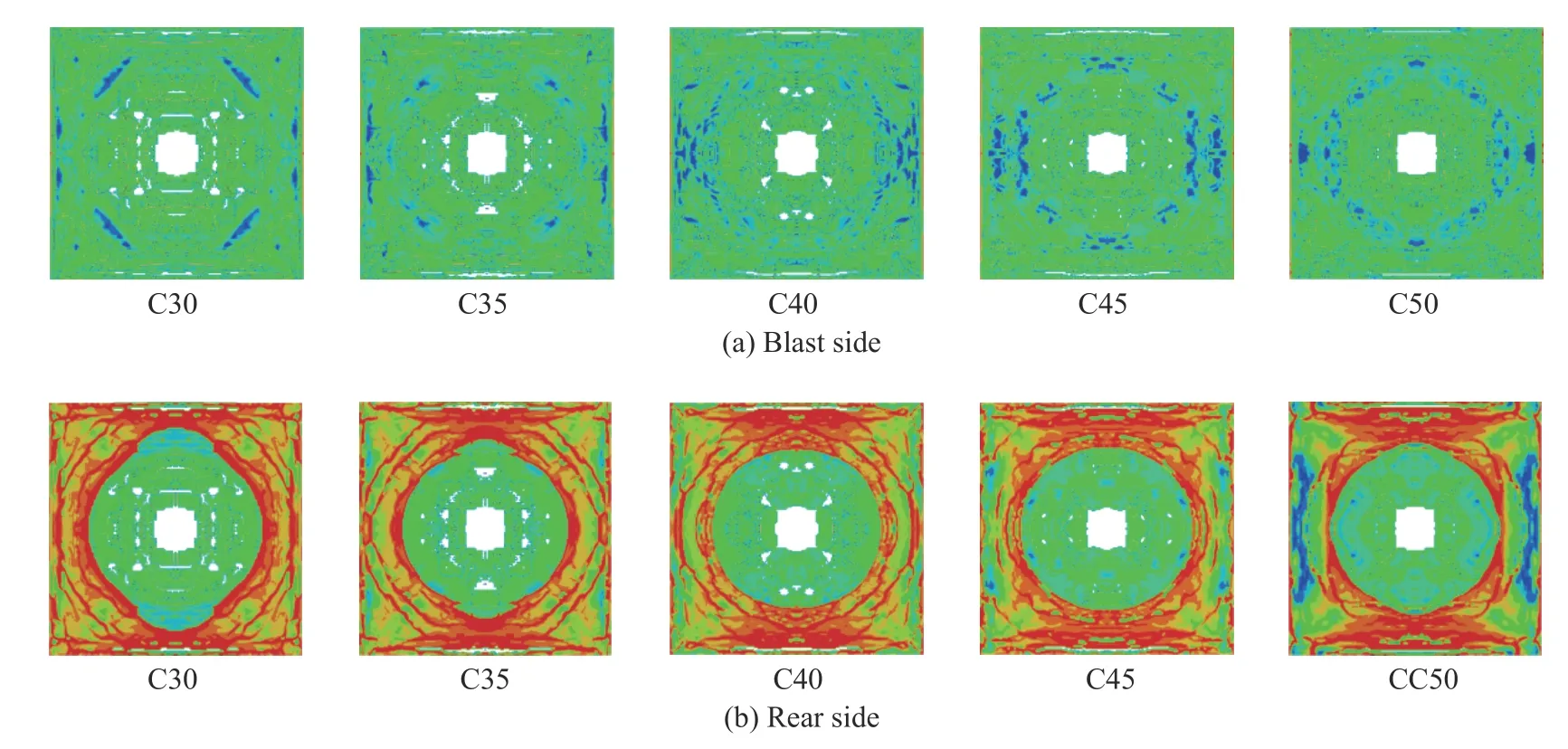
图23 不同混凝土强度时SCS混凝土的有效塑性应变Fig.23 Effective plastic strains of concrete in SCS with different concrete strengths

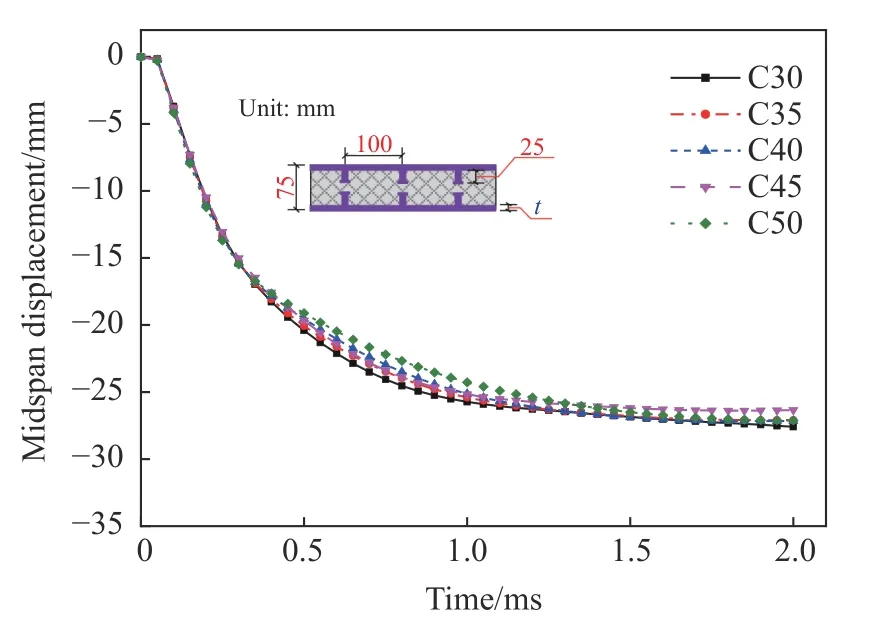
图24 不同混凝土时SCS的跨中位移曲线Fig.24 Mid-span displacement curves of SCS with different concrete strengths

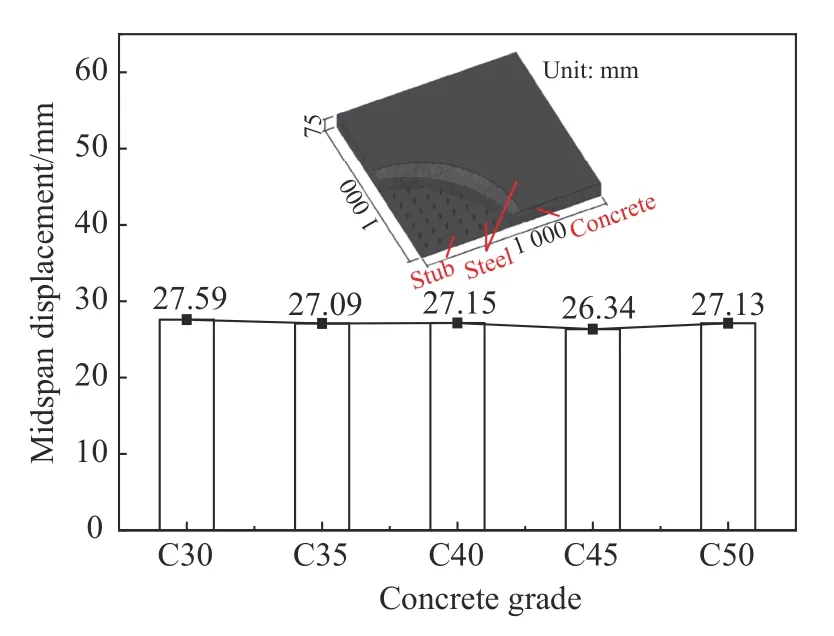
图25 不同混凝土时SCS的跨中最大位移Fig.25 Maximum displacement of SCS with different concrete strengths

4.3 钢板厚度

钢板厚度分别为2.0、2.5、3.0、3.5和4.0 mm，其余参数均保持不变，分析不同钢板厚度下组合板SCS的爆炸响应。图26为不同钢板厚度下钢-混凝土-钢组合板中混凝土的有效塑性应变。不同钢板厚度下，组合板混凝土部分均发生贯穿破坏，迎爆面及背爆面塑性损伤区域随钢板厚度的增加逐渐增大，迎爆面靠近自由边区域损伤程度逐渐增大，背爆面环形裂缝位置随钢板厚度增加逐渐向四周发散。由图27可见，随着钢板厚度的增加，钢板跨中最大位移呈减小的趋势，钢板厚度增加与跨中位移减小呈近似线性关系。由图28可见，钢-混凝土-钢组合板板底跨中峰值加速度减小与钢板厚度增加呈非线性。上述现象表明，钢板厚度的增大明显减小了组合板跨中位移，钢板厚度是影响钢-混凝土-钢组合板抗爆性能的显著因素。

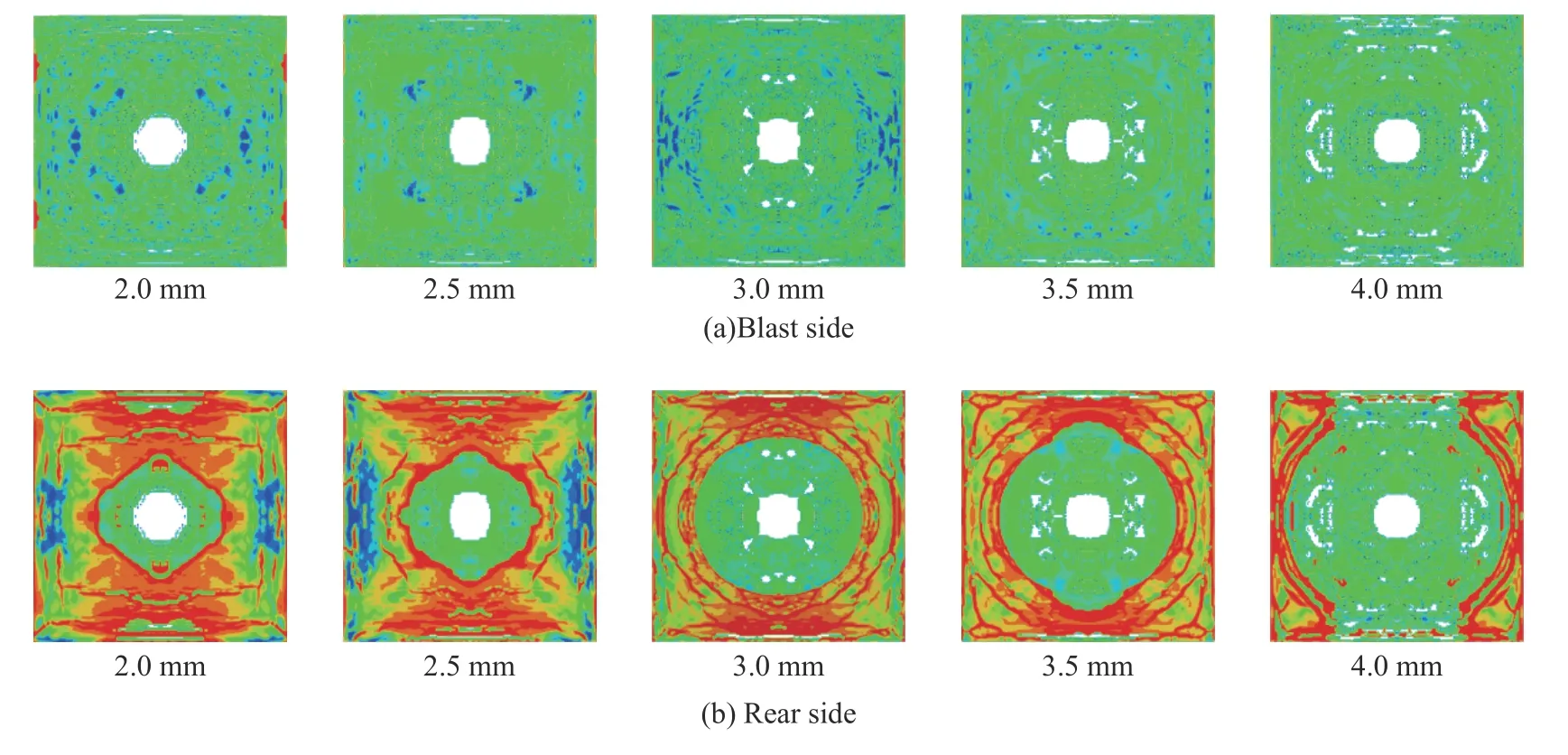
图26 不同钢板厚度时SCS混凝土的有效塑性应变Fig.26 Effective plastic strains of concrete in SCS with different thickness of steel plate

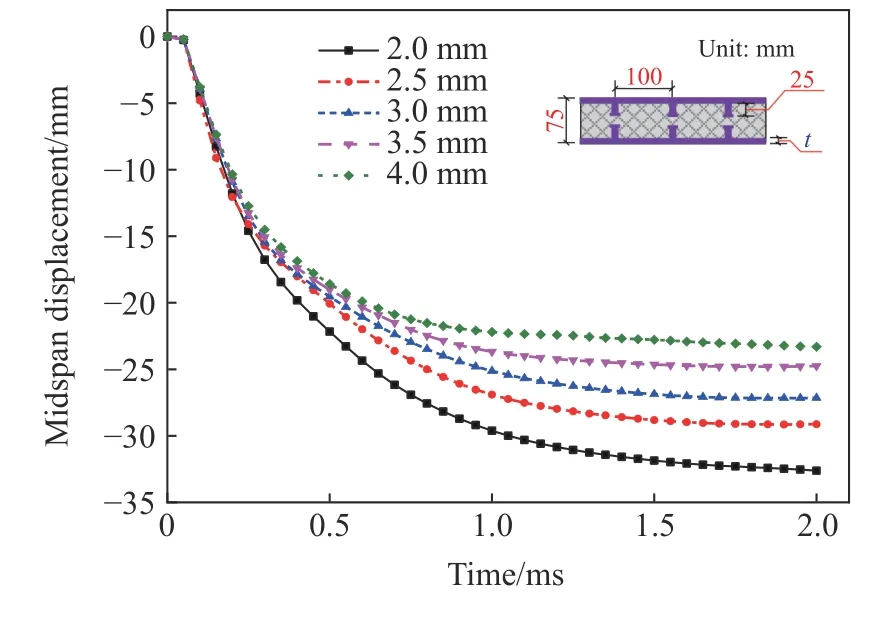
图27 不同钢板厚度时SCS的跨中位移曲线Fig.27 Mid-span displacement curves of SCS with different thicknesses of steel plates

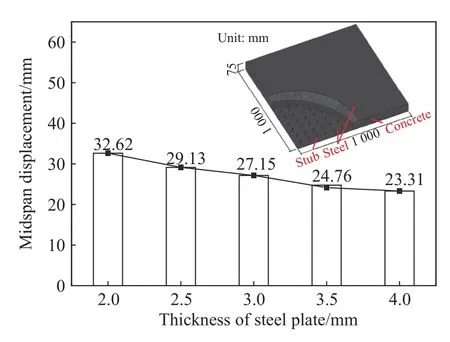
图28 不同钢板厚度时SCS的跨中最大位移Fig.28 Maximum displacements of SCS with different thicknesses of steel plates

5 挠度计算公式

为了准确预测接触爆炸作用下钢-混凝土-钢组合板的挠度，基于参数分析得到的药量-钢板厚度-跨中挠度数据，通过多元非线性回归分析获得钢-混凝土-钢组合板的跨中挠度经验公式，并给出拟合曲线，通过曲线和公式可以判断在不同药量和钢板厚度下组合板跨中变形情况。

组合板的尺寸为1 000 mm×1 000 mm×75 mm，试件的混凝土为C40，剪力连接件长度为3 mm，炸药位于组合板中间位置。基于数值分析结果，炸药量分别为100、150、200、250和300 g，钢板厚度分别为2.0、2.5、3.0、3.5和4.0 mm，拟合得到跨中最大挠度γ与炸药量w和钢板厚度t之间的计算公式。

组合板跨中挠度计算公式为：

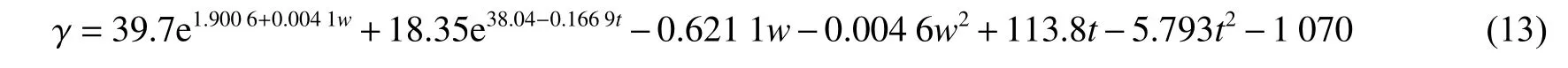
式中：γ为组合板跨中挠度，mm；w为炸药量，g；t为钢板厚度，mm。

图29为钢-混凝土-钢组合板最大挠度与药量、钢板厚度的三维曲面图，表3为组合板跨中挠度经验公式拟合结果误差分析。可见，拟合公式结果与数值分析结果误差较小，误差不超过11%，相关系数R2=0.991 1，表明挠度计算公式非常接近数值计算结果，该公式能够很好地拟合组合板跨中挠度与炸药量、钢板厚度之间的相互关系。

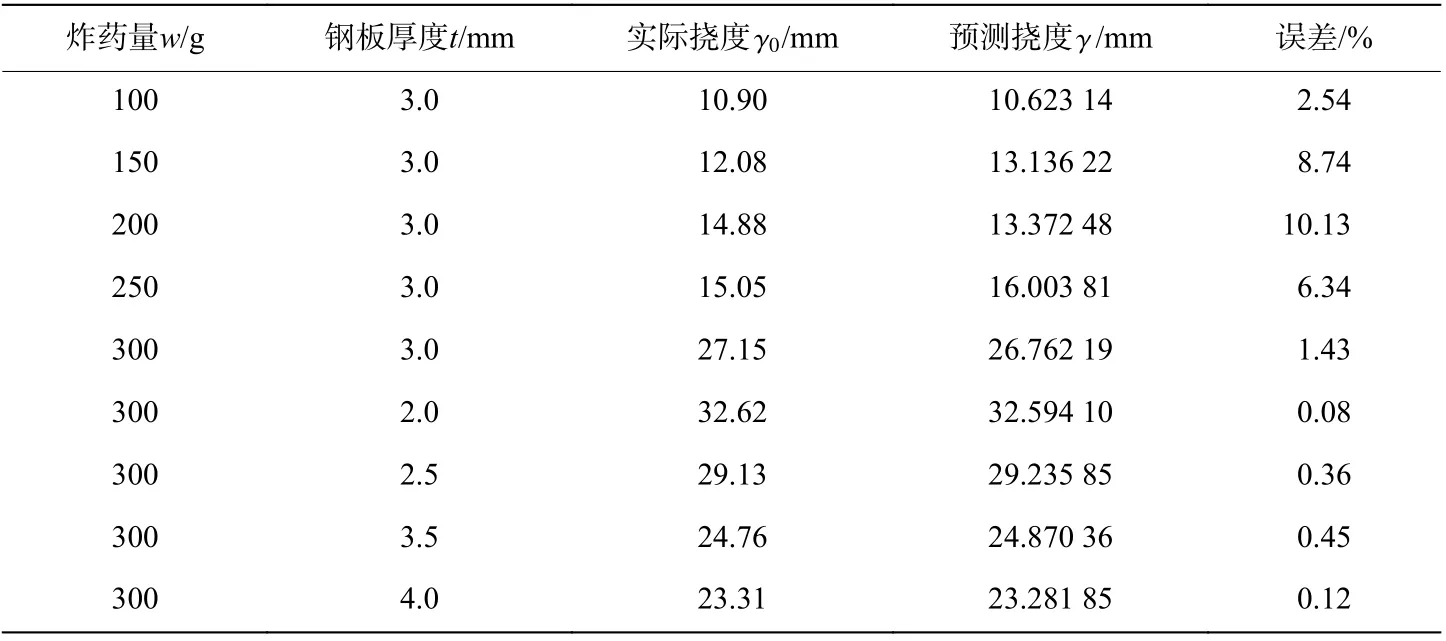
表3 混凝土-钢-混凝土组合板跨中挠度经验公式拟合结果Table3 Fitting results of empirical formula for mid-span deflection of SCS

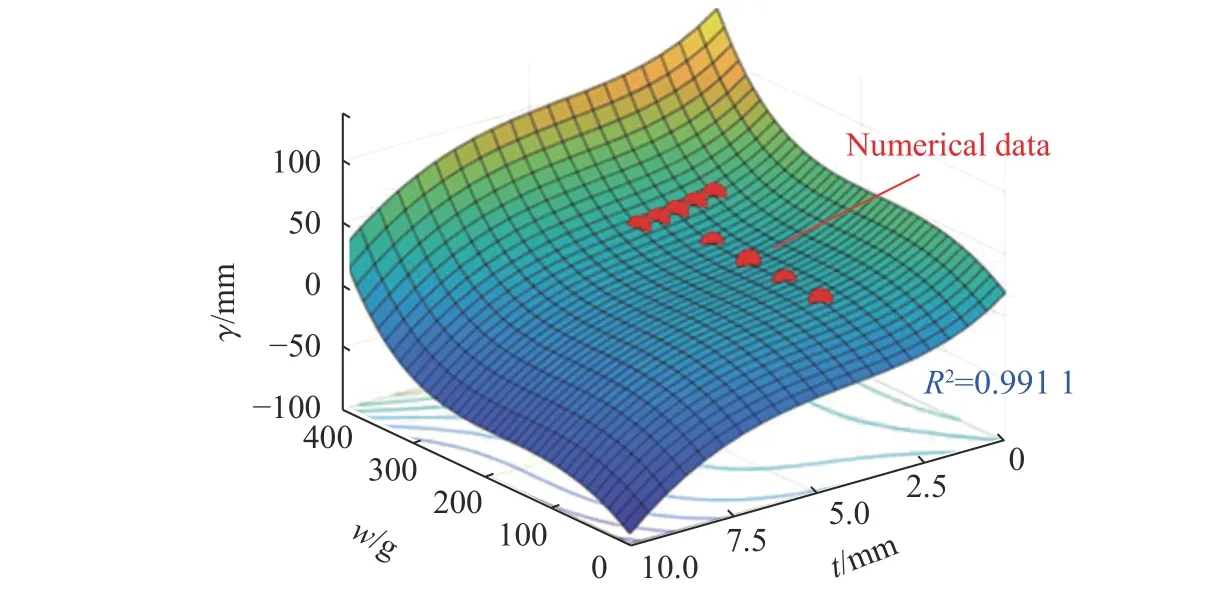
图29 SCS跨中挠度与炸药量、钢板厚度的关系Fig.29 Mid-span deflections of SCS versus explosive charges and thicknesses of steel plates

6 结 论

设计并制作了钢筋混凝土板和双钢板混凝土板试件，研究了双钢板混凝土组合板的损伤模式、跨中最大挠度和测点峰值加速度等，并与实验结果对比、分析，验证了有限元分析模型的准确性。参数化分析了炸药量、混凝土强度和钢板厚度等参数对双钢板混凝土组合板抗爆性能的影响规律，提出了双钢板混凝土组合板跨中挠度计算公式，结果论如下。

（1）接触爆炸作用下，钢筋混凝土板和双钢板混凝土板破坏模式不同：钢筋混凝土板发生冲切破坏，爆坑内钢筋裸露，背爆面产生混凝土震塌现象,板面贯穿，丧失承载能力；双钢板混凝土板起爆点处上侧钢板发生塑性，产生局部屈曲破坏，由于两侧钢板的包裹，整体性基本保持完好，同时没有产生混凝土飞溅。

（2）钢筋混凝土板试件迎爆面和背爆面爆坑及跨中挠度数值与实验结果误差分别为16.6%和7.6%，钢筋混凝土板数值模型能较合理地模拟钢筋混凝土板的破坏情况和钢筋变形情况。双钢板混凝土组合板迎爆面爆坑和跨中挠度数值与实验结果误差分别为10.7%和21.7%，数值模型对于模拟钢-混凝土-钢组合板的损伤情况、位移及加速度响应合理有效。

（3）随着混凝土强度的增加，钢筋混凝土板破坏情况呈先减小后增大的趋势，双钢板混凝土板混凝土部分塑性损伤面积逐渐减小,板底跨中最大位移呈波动变化。提高混凝土强度并不能显著改善双钢板混凝土组合板的抗爆性能，而增加钢板厚度可以显著增强双钢板混凝土组合板的抗爆性能。

（4）利用非线性拟合和回归分析的方法，获得了双钢板混凝土组合板跨中挠度与药量和钢板厚度的计算公式，计算结果与实验和数值分析结果比较接近，误差小于11%，相关系数R2=0.991 1。计算公式可以较准确预测接触爆炸作用下双钢板混凝土组合板跨中变形挠度。需要注意的是该公式主要适用于本文研究的双钢板混凝土组合板，其他类型板需要单独进行分析。