基于SHPB实验的砂岩动态破坏过程及应变-损伤演化规律研究*
张明涛,王 伟,王奇智,张思怡
(1.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室,河北 石家庄 050043;2.河北省金属矿山安全高效开采技术创新中心,河北 石家庄 050043;3.石家庄铁道大学土木工程学院,河北 石家庄 050043;4.河北科技大学建筑工程学院,河北 石家庄 050018)
砂岩型铀矿爆破增渗地浸开采效率在很大程度上依赖赋矿岩层的整体损伤程度和裂纹分布情况,足够的裂纹数量且均匀分布才能保证溶浸液在赋矿岩层中顺利流通且与铀元素充分接触反应[1-3]。因此,研究砂岩试样在冲击荷载作用下的破坏机理、裂纹分布和损伤演化规律具有重要意义。在岩石破坏机理方面:Lundberg[4]利用SHPB实验装置,研究了岩石在应力波作用下的破碎状态,发现在冲击荷载作用下,岩石的裂纹沿着轴向扩展,且随着动荷载的增加,裂纹的破碎程度也随之增加,破坏后的岩样呈对称圆锥体破坏形式;宫凤强等[5-6]利用改造的三轴SHPB装置,研究了砂岩在一维和三维动静组合加载作用下的破坏模式,发现常规冲击下岩石的临界破坏模式为劈裂形式,一维动静组合加载下呈现压剪形式,三维动静组合加载下岩石的破坏形式在高低应变率下表现出不同的破坏状态;金解放等[7]利用SHPB装置,研究了循环冲击荷载作用下岩石的破坏模式和破坏机理,发现随着冲击次数的增加,岩石发生破坏的形态和机理也随之不同;刘希灵等[8]研究了花岗岩、石灰岩、红砂岩3种岩石在不同应变率下的破坏状态,发现冲击载荷下随着应变率的增加,3种岩石试样的破碎程度有所增大,碎块的尺寸减小、块数增加、碎屑增多。在岩石损伤研究方面:高文学[9]系统研究了岩石的动态损伤特性,基于实验结果,通过引入声波衰减系数与损伤能耗散率的关系,首次运用能量法建立了岩石动态损伤模型;Liu等[10]基于连续介质力学、统计断裂力学,并定义在给定裂纹密度下破裂的发生概率为损伤变量D,提出了一个岩石各向同性爆破损伤的模型;随着X射线断层扫描(CT)技术在岩石损伤力学方面的发展和成熟,损伤后岩石内部不同切面上的裂纹扩展情况可直观地展现出来,并可通过后处理得到岩石内部的裂纹数量及裂纹密度;Raynaud等[11]利用X射线CT扫描技术,对岩石样品内部的裂隙进行无损扫描,观测了岩石样品在三维受力状态下内部发生的静态变形和断裂;Kawakata等[12-13]结合岩样端面的CT扫描数据,建立了三维CT图像,直观展现了裂纹的分布与形态;Huang等[14]通过CT扫描和三维成像技术,成功提取了花岗岩破坏过程中不同应变下的裂纹体积,为在细观上研究岩石的损伤演化规律提供了很好的方法。
目前,对岩石的动态破坏特征和损伤演化规律的研究,多以不同应变率下或循环冲击状态下岩石的破坏状态为基础而展开分析[15-16],这两种方法在严格意义上并不能代表岩石在相同破坏过程中的损伤演化规律。前者采用不同的冲击速度,显然不满足在相同条件下这个要求;后者为实验方法,在对岩石的重复冲击过程中,岩石前面状态的损伤势必会影响后面损伤的产生,也不能严格代表岩石在相同破坏过程中的损伤演化。因此,本文中,利用带有应变控制环的SHPB实验系统,对砂岩试样进行不同应变级别下的动态冲击实验,对砂岩试样的破坏过程、破坏机理和裂纹分布状态进行研究;基于波速测试实验和CT扫描实验,分别从宏观和细观两方面研究砂岩的损伤演化规律,构建冲击荷载作用下砂岩的应变-损伤定量关系式,并研究砂岩试样在冲击荷载作用下的损伤演化规律。研究成果可为揭示动荷载作用下砂岩的破坏机理、裂纹分布形态和损伤演化规律提供理论参考。
1 实验装置及试样制备
1.1 实验装置
实验在分离式霍普金森(SHPB)实验系统上完成,为了达到本实验的研究目的,在原有的SHPB实验系统上安装了应变控制环,SHPB系统的总体及实物如图1~2所示。该实验系统的子弹、入射杆、透射杆长度分别为300、3 000、2 000 mm,直径均为50 mm,材质均为40Cr合金钢,密度为7 810 kg/m3,纵波波速为5 410 m/s,弹性模量为210 GPa,泊松比为0.23。
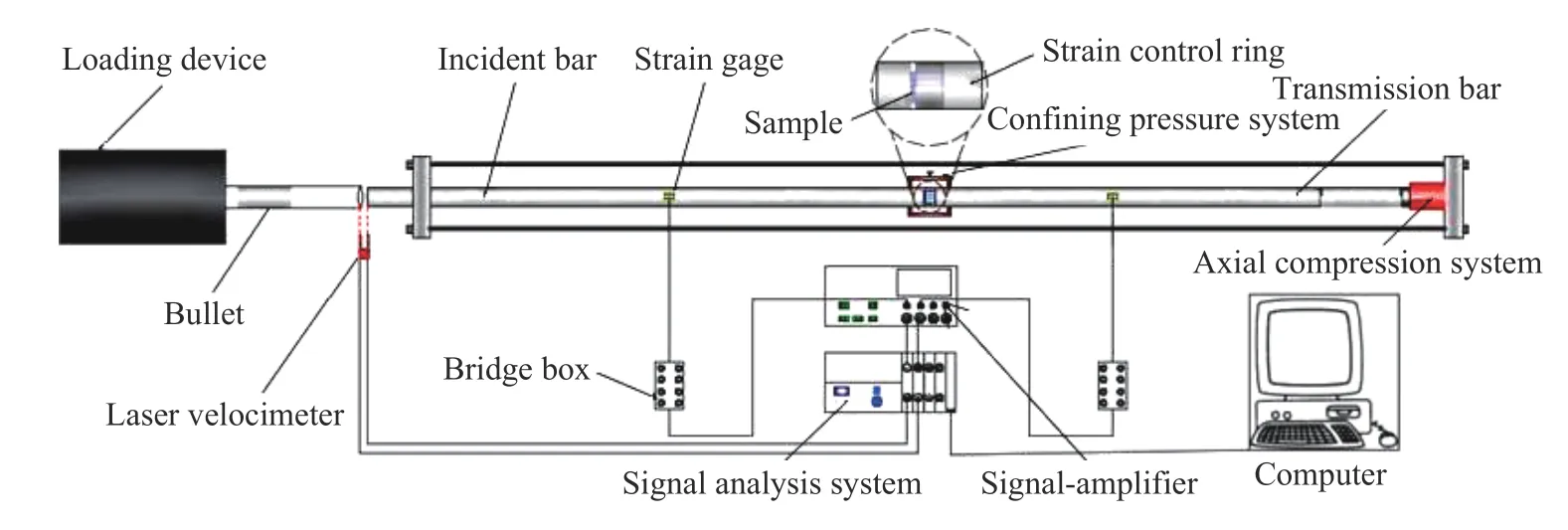
图1 SHPB实验系统组成Fig.1 Diagram of SHPB experimental system

图2 SHPB实验系统照片Fig.2 Photo of SHPB experimental system
应变控制环的内外直径分别为34、50 mm,长度为30 mm,材质选用刚度较大的Cr12,利用带有应变控制环的SHPB实验系统,可以实现对岩石在动态冲击变形过程中应变的控制[14]。图3为应变控制环与锁扣实物图,用锁扣将应变控制环固定在透射杆的入射端,将岩石两端均匀涂抹凡士林后固定在入射杆和透射杆之间的应变控制环内,如图4所示。由于砂岩试样长于应变控制环,因此在入射杆和应变控制环之间将存在长度Δ的间距,冲击实验时入射杆先接触砂岩试样的入射段,试样将会产生长度Δ的变形,随后入射杆便会与应变控制环接触,此时刚度较大的应变控制环将承担入射杆的冲击荷载,阻止入射杆对试样的冲击作用,使试样的冲击变形控制为相对应的间距Δ,通过设定不同长度的砂岩试样,以此来得到不同应变下砂岩试样的破坏状态。

图3 应变控制环与锁扣的照片Fig.3 Photos of strain control ring and lock catch
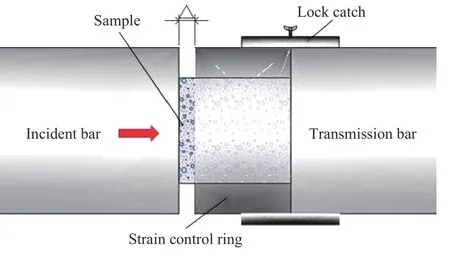
图4 应变控制环组成Fig.4 Diagram of strain control ring
1.2 试样制备
所用试样均取自一块完整性和均质性较好的砂岩,该砂岩的基本物理力学参数见表1。先加工若干块直径为25 mm、长度不小于30.10 mm的砂岩试样。为了利用控制应变环来研究砂岩的动态破坏过程、破坏机理和损伤演化规律,根据长度30 mm、直径25 mm的完整砂岩试样在常规冲击作用下的最大应变,确定了8组不同应变级别下的试样尺寸,长度分别为30.05、30.10、30.15、30.20、30.25、30.30、30.35和30.40 mm,直径均为25 mm,其长径比约为1.2,能有效保证试样在动态加载过程中两端的受力平衡。

表1 砂岩基本物理力学参数Table1 Basic physical and mechanical parameters of gray sandstone
以上8组不同应变级别下砂岩试样的尺寸精度要求较高,为0.05 mm。因此,采用精确度为0.01 mm的SHM-200型双端面磨石机,对初步制作的砂岩试样进行精细打磨,利用精度0.02 mm的电子游标卡尺,对打磨的试样长度进行不同部位的测量。与此同时,保证试样端面的不平行度和不垂直度均小于0.02 mm,8组尺寸下每组试样打磨3块,共24块,打磨后的砂岩试样如图5所示。

图5 打磨后的砂岩试样Fig.5 Sandstone samples after grinding and finishing
2 基于应变控制的砂岩动态破坏过程分析
在进行砂岩试样控制应变动态冲击实验前,先对砂岩破坏特征的应变率效应进行探究。通过实验确定了5组应变率分级,分别为37.101、40.527、56.024、68.336、79.901 s−1,在不同应变率冲击作用下砂岩试样的破坏特征如图6所示。
由图6可知:在低应变率37.101 s−1下,砂岩试样的破坏形式以剪切破坏为主,试样外表皮出现薄薄的、大片块状型的岩石脱落,试样外围中间部分呈现小块颗粒及粉末状破碎状态,并且整体初步表现了双锥形破坏状态;随着应变率的增加,在应变率40.527和56.042 s−1下,外表皮大片块状型碎片和小块颗粒及粉末数量明显增多,且连接的双锥形部分分离,形成两个独立的锥形部分,但透射端锥形部分明显大于入射端锥形部分。同时,外围片状部分和锥形部分出现了明显的裂纹,如图7所示,经分析,该裂纹为外围片状部分和锥形部分受到纵向高速冲击压缩产生了较大的横向变形而导致。在高应变率68.336和79.910 s−1下,出现的裂纹(见图7)会随着冲击应变率的增加继续延伸和扩展,导致试样锥形部分变小直至消失,外围片状碎块破碎尺度明显减小,数量增多,在试样外围中间内部的破碎区内细小碎块及粉末逐渐增多,整体完全破碎状态如图6(d)~(e)所示。由图7可知,随着应变率的增加,外表碎片部分和锥形部分陆续受到高速的冲击压缩而导致横向拉伸而破坏,属于张拉破坏形式。对不同应变率下砂岩试样破坏特征的分析可知,砂岩在动荷载作用下的主要破坏形式为由小应变率下的剪切破坏转变为较高应变率下的剪切-张拉混合破坏。

图6 不同应变率下砂岩的破坏特征Fig.6 Failure characteristics of sandstones under different strain rates

图7 横向拉伸引起的裂纹Fig.7 Cracks caused by transverse tension
为得到不同应变级别下砂岩试样的破坏状态,利用带有应变控制环(长度30 mm)的SHPB实验系统,对长度30.05、30.10、30.15、30.20、30.25、30.30、30.35和30.40 mm的砂岩试样进行动态冲击实验,共8组,每组尺寸进行3次实验,防止因岩石内部缺陷而带来实验结果的离散性。由图6可知,在应变率68.336 s−1下砂岩试样恰好呈完全破碎状态,因此在控制应变冲击实验中统一选取恰好使砂岩试样达到完全破碎时的应变率68.336 s−1,即在气压0.069 MPa下对不同控制应变级别下试样进行动态冲击实验。图8为砂岩试样在应变0.001 7、0.003 3、0.005 0、0.006 6、0.008 3、0.009 9、0.011 5、0.013 1下的动态破坏状态。随着冲击应变的增加,前期岩石并没有明显的破坏状态,而后期砂岩试样的破坏程度突然增加,直到最终完全破坏(见图8(h))。此时,继续增大冲击应变,砂岩试样的破坏状态几乎保持不变,它与在同应变率常规动态冲击下试样的破坏状态的不同之处主要在于,常规冲击下试样最终破坏状态不存在锥形部分,而在应变控制环冲击状态下存在锥形部分。其原因为,常规动态冲击过程中在试样大部分破坏后,锥形部分由于入射杆的惯性作用而受到二次冲击伤害,导致锥形部分破碎,在带有应变控制环冲击状态下,在试样大部分破坏后,应变控制环将承载入射杆由于惯性作用产生的二次冲击作用力,因此,锥形部分受到了保护而保持相对完整。

图8 不同控制应变下砂岩试样的破坏状态Fig.8 Failure states of sandstone samples under different controlled strains
由图8(a)~(b)可见,在应变0.001 7、0.003 3下,砂岩试样外表并没有出现破碎现象,岩样几乎呈完整状态。由图8(c)~(d)可见,在应变0.005 0、0.006 6下,砂岩试样仅在端面外围出现了微小的破碎痕迹,其余部分较为完整。由图8(e)可见,继续增加应变,在应变0.008 3下,砂岩试样端部外围出现了明显的破碎现象,伴随有微小的碎片脱落,且初步表现出了剪切破坏的痕迹。由图8(f)可见,在应变0.009 9下,砂岩试样发生了明显的剪切破坏,伴随有碎片和粉末脱落,外表碎片大部分保持大块完整状且还未完全与内部双锥形部分分离,透射段锥形部分大于入射段锥形部分。由图8(g)可见,在应变0.011 5下,砂岩试样外表片状碎块与双锥形部分完全分离,大块的片状碎块破碎,小块颗粒及粉末增多,双锥形破坏形式已明显呈现,此时入射段锥形部分已经发生破坏,透射段锥形部分表面已出现明显裂纹。由图8(h)可见,在应变0.013 1下,双锥形部分已完全分离,外表片状碎块、细小颗粒和粉末都明显增多,入射段小锥形部分和透射段大锥形部分都发生了不同程度的破坏。如果在该冲击状态下没有应变控制环承载入射杆产生的二次冲击力,锥形部分将会受到二次冲击作用而发生完全破坏,其最终破碎形式将会与图6(d)的一样。
由图8可知,在应变0.011 5、0.013 1下,砂岩试样已发生了明显的破坏状态,破坏特征可直接观察到,但由于在应变0.001 7、0.003 3、0.005 0、0.006 6、0.008 3、0.009 9下,砂岩试样整体性并未破坏,内部是否发生破坏以及破坏形式不得而知。因此,基于岩石声波波速测试结果,在6组中选取具有代表性的砂岩试样进行CT扫描实验,每个砂岩试样的CT扫描横向切片约1 220个,为了观察砂岩试样内部的整体破坏情况,分别提取试样的上部、中部、下部以及纵向切片扫描图,用以分析试样内部的破坏特征及裂纹分布情况,不同应变冲击下砂岩试样CT扫描结果如图9~14所示。
在CT扫描切片图中,密度越大的物质所在区域的图像灰度值越大,图像亮度越高,反之亮度越低,孔隙或裂隙存在区域为黑色。由图9~10可见,在应变0.001 7、0.003 3下,试样内部整体未见明显裂隙;由图11可见,在应变0.005 0下,仅在试样上下两端面出现了微小的颗粒脱落,其余部分未见明显裂隙;由图12可见,在应变0.006 6下,在试样两端的外围出现了较小的环向裂隙,两端外围亮度较高,表明试样在动态冲击过程中该部分受纵向压缩导致密度较大,裂隙先从试样两端面的外围发生起裂,试样其余部分未见明显裂隙;由图13可见,在应变0.008 3下,试样两端面颗粒脱落明显增多,试样上部、中部及中下部外围出现若干径向微裂隙,该裂纹是由试样受压缩导致横向变形而产生,其他位置未见明显裂隙;由图14可见,在应变0.009 9下,砂岩试样内部的破坏程度突然较明显,试样内部存在贯穿的主裂隙以及若干次生的微裂隙,径向裂隙条数增多并伴随有环状裂纹的产生。由以上分析可得,砂岩试样在动态冲击过程中,裂纹的产生、扩展和试样的变形并不是正比例关系,而是随着应变的增加大致分为3个阶段:无裂纹阶段(应变0~0.003 3)、微裂纹起裂阶段(应变0.003 3~0.008 3)和裂纹贯通阶段(应变0.008 3~0.009 9),主要裂隙为偏内部的环向裂纹和外围的径向裂纹,且裂纹集中区域主要分布在试样中间外围,最终使砂岩试样呈近似的双锥形破坏。

图9 在ε=0.001 7冲击下试样CT扫描图Fig.9 CT scans of the sample under impact at ε=0.001 7

图10 在ε=0.003 3冲击下试样CT扫描图Fig.10 CT scans of the sample under impact at ε=0.003 3

图11 在ε=0.005 0冲击下试样CT扫描图Fig.11 CT scans of the sample under impact at ε=0.005 0
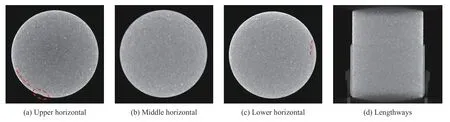
图12 在ε=0.006 6冲击下试样CT扫描图Fig.12 CT scans of the sample under impact at ε=0.006 6
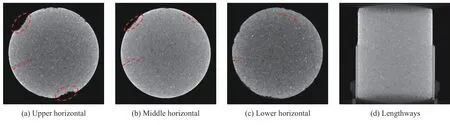
图13 在ε=0.008 3冲击下试样CT扫描图Fig.13 CT scans of the sample under impact at ε=0.008 3
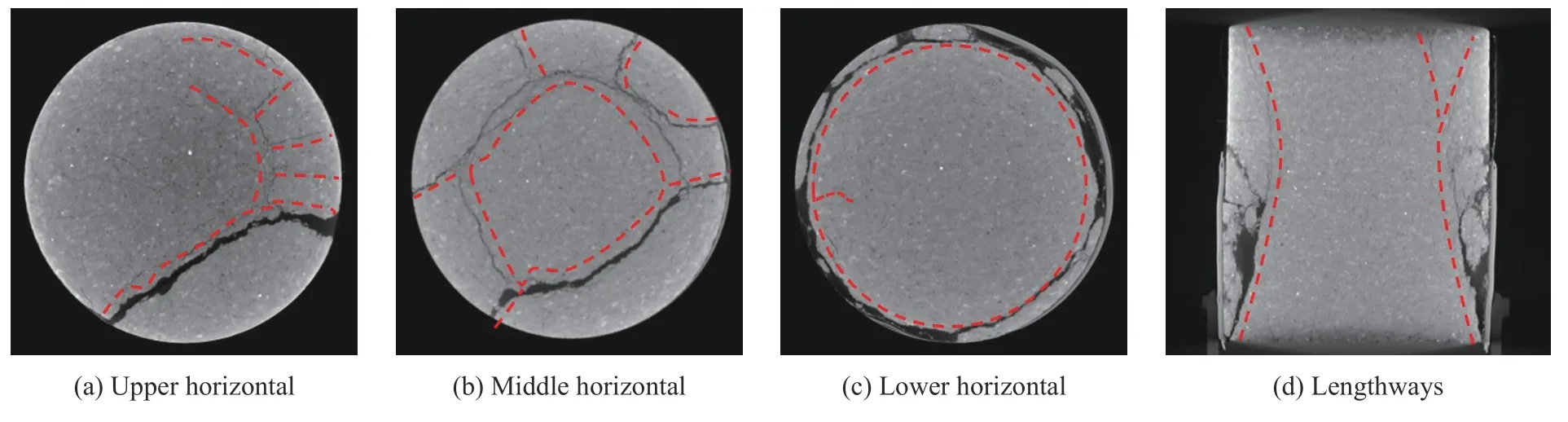
图14 在ε=0.009 9冲击下试样CT扫描图Fig.14 CT scans of the sample under impact at ε=0.009 9
通过砂岩破坏过程及内部裂纹扩展的分析,总结了砂岩试样在冲击荷载作用下的破坏机理:在SHPB冲击实验过程中,虽然在砂岩试样两端均匀涂抹了一层薄薄的凡士林,但由于瞬时冲击荷载非常大,即使接触面动摩擦因数很小,同样也会产生较大的端面摩擦力,因此杆件和试样之间的端面摩擦力不可忽略。图15为砂岩试样的冲击破坏示意图,Fd为冲击荷载,f为端面摩擦力。当试样在受到纵向动态压缩时,因泊松效应势必会产生横向变形;但由于端面摩擦力的存在,试样两端的横向变形将会受到限制,只有试样中间部分可以相对自由地发生横向变形;因此在该情况下,当横向变形达到砂岩试样的最大应变值后,便会产生剪切破坏面(见图15),形成以共轭双曲线形式为主的破坏模式。图15中绿色区域部分的砂岩受到冲击压力会迅速破碎,形成试样的破碎区域,留下中间的近似双锥形区域较完整,在自然界中也存在这种近似双锥形破坏的支撑石柱,如图16所示。若在冲击实验中砂岩试样没有应变控制环的保护,其双锥形区域也会受到冲击压缩而产生张拉破坏,因此在冲击破坏过程中,砂岩试样将先发生剪切破坏,紧接着发生压缩破坏,所以整体破坏模式为剪切-张拉混合破坏。
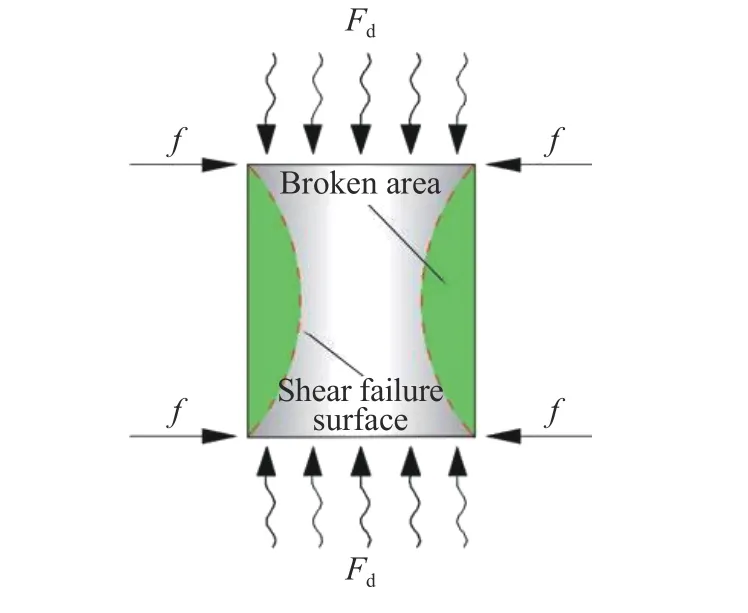
图15 试样破坏示意图Fig.15 Schematic diagram of sample failure
3 基于应变控制的砂岩损伤演化规律研究
损伤变量是表征结构内部劣化程度和力学特性的量化参数,是研究岩石损伤过程和演化机制的前提和基础,对岩石损伤变量的定义主要分为两大类:一类为损伤变量的细观定义,主要从岩石内部微裂纹的体积、等效面积、数目、长度等定义损伤变量;另一类为损伤变量的宏观定义,主要从岩石的弹性模量、声波波速、单位体积耗散能等宏观参数方面对损伤变量加以定义[17]。结合各损伤变量法的特点,将分别利用声波波速损伤定义法(宏观损伤变量法)和裂纹密度损伤定义法(细观损伤变量法),研究砂岩在冲击荷载作用下的损伤演化规律。
3.1 基于波速测试实验的宏观损伤演化规律研究
岩石中波速传播情况能较好反映岩石的整体强度特征、致密程度和裂纹扩展等情况。利用HSYS4A型岩石声波参数测试仪及其配套的纵波发接探头,对不同应变冲击实验前、后的试样进行声波测试。声波波速测试过程中,将声波发射探头和接受探头紧贴砂岩试样两端面,且在接触面上均匀的涂抹一层薄薄的凡士林以增加耦合性,将测得的砂岩试样在冲击荷载作用前、后的声波波速vf、va,代入公式D=1−(va/vf)2,便可得到不同冲击应变作用下砂岩的损伤变量D[17-18],测试结果见表2。
在声波波速损伤定义中,由于破碎状态下试样的波速测试已无法进行,因此通常定义破碎状态下试样的损伤变量D为1。对表2中的应变、损伤数据进行处理,拟合曲线如图17所示。损伤变量随应变的变化趋势大致分为2个阶段:第1个阶段为损伤缓慢发展阶段,随着应变的增加,损伤变量增长较平缓,应变从0到0.008 3变化过程中,损伤只增长了约0.2,该阶段损伤增量只占整体损伤的20%左右;第2阶段为损伤快速发展阶段,当应变达到0.008 3后,少许的应变增加,损伤变量快速增长,应变从0.008 3到0.011 5变化过程中,损伤变量迅速从0.2增长到了1,该阶段损伤增量约占了砂岩试样整体损伤的80%。表现在试样的破坏特征上,从未出现明显破坏到试样突然整体破坏,该损伤演化规律与观察到的砂岩试样破坏过程一致。在波速测试实验中,纵波是沿试样的轴向方向进行传播的,由图8可见:在第1阶段,砂岩试样在单轴动态冲击作用下,主要产生沿试样轴向方向的微小裂纹,而没有出现对纵波阻碍作用较强的横向裂纹,因此纵波波速在该阶段下降较缓慢,对应于损伤发展较缓慢;在第2阶段,砂岩试样整体出现了较明显的共轭双曲线型的裂纹,在一定区域上对纵波的传播产生了较大的阻碍作用,因此在第2阶段纵波波速下降较迅速,对应于损伤发展较迅速。通过对应变-损伤变化规律的分析,可知损伤随应变的增长呈指数型增长,利用指数型函数进行拟合,得到应变-宏观损伤变量之间的函数关系:
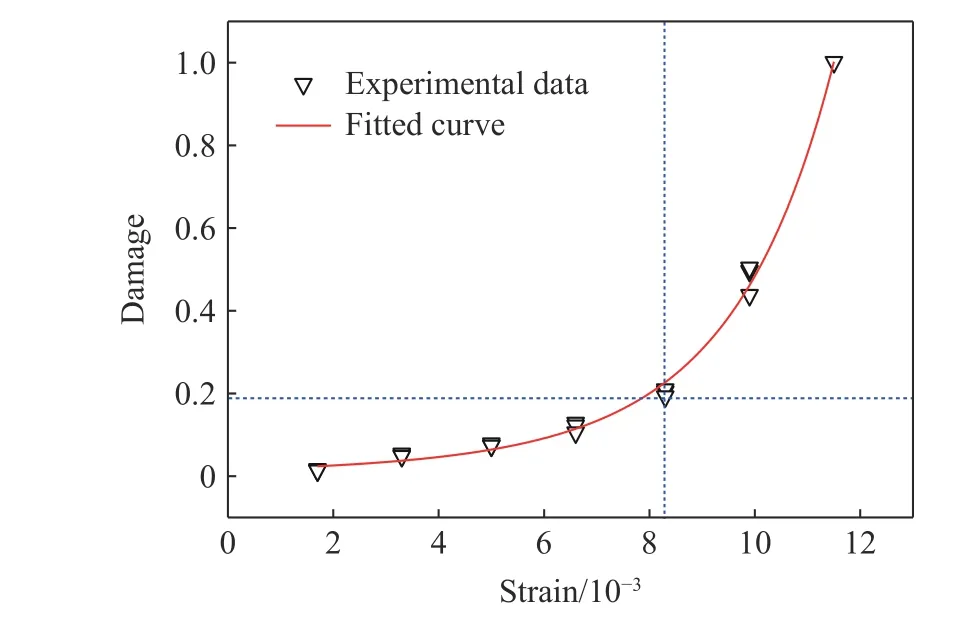
图17 声波测速实验数据及其拟合曲线Fig.17 Experimental data and fitting curve of acoustic velocity measurement
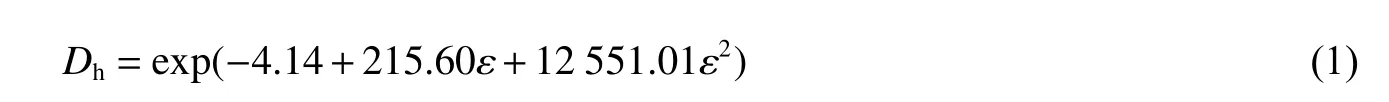
式中:Dh为砂岩的宏观损伤变量,ε为砂岩在冲击荷载作用下的应变。
式(1)的拟合优度R2=0.996 92,拟合效果较好,通过此关系式可以搭建砂岩应变与宏观损伤变量之间的定量关系式,通过应变参数便可以较容易地求出砂岩在冲击荷载作用下的宏观损伤变量。相对其他损伤变量关系式,该关系式大大简化了损伤变量的求解过程。
3.2 基于CT扫描实验的细观损伤演化规律研究
CT扫描实验利用微焦点3D计算机断层扫描系统进行,如图18所示。该实验系统采用三英nanoVoxel-2000 X射线三维显微镜,其分辨率高达24.01 µm,完全满足本次岩石内部损伤状态的CT扫描要求。在天然状态下,岩石内部含有大量微小裂纹、空隙,由裂纹密度损伤变量定义公式D=V/V0(V为损伤岩样中裂纹的总体积,V0为岩石在自然状态下的总体积)可知,为了更准确地利用裂纹密度来研究岩石的损伤演化规律,应先检测未受冲击作用的砂岩试样的裂纹密度。图19为砂岩试样未受冲击作用的三维重构图,该计算机图像处理技术将试样的无损部分设定为黑色,损伤部分设定为亮蓝色。由图19可见,砂岩试样三维重构图内部均匀黑色分布,并未出现亮蓝色部分,利用Avizo 8.1软件,以砂岩三维重构图为基础,对其内部的空隙、裂纹和砂岩颗粒进行区分、提取和计算,得到原始砂岩试样内部的孔隙率为0.001 1%,几乎可以忽略。所以,原始砂岩试样内部基本无初始损伤,砂岩试样整体均匀性良好。

图18 微焦点3D计算机断层扫描系统Fig.18 Microfocal 3D computed tomography system

图19 无损砂岩试样三维重构图Fig.19 Three dimensional reconstruction of non-destructive sandstone samples
在应变0.011 5、0.013 1下,砂岩试样发生了整体性的破坏,已无法进行CT扫描及图像三维重构;在应变0.001 7、0.003 3、0.005 0、0.006 6、0.008 3、0.009 9下,砂岩试样整体性较完整,为了得到由内部裂纹造成的试样孔隙率,即裂纹密度,基于砂岩试样声波波速测试结果,使用相同的扫描参数对每组应变中具有代表性的砂岩试样进行CT扫描,利用VoxelStudio Recon软件重建CT扫描数据,生成Raw数据体,利用Avizo 8.1后处理软件对数据体进行阈值分割、孔隙提取及三维体渲染等操作,生成三维可视化渲染图,如图20所示。对于存在裂隙的数据体进行孔隙三维几何特征计算,包括孔隙体积、孔隙表面积等,CT扫描损伤测试结果见表3。

图20 三维可视化渲染图Fig.20 Three dimensional visual rendering
由于完全破碎状态下的砂岩试样无法进行CT扫描实验及图像三维重构,因此定义完全破碎状态下砂岩试样的损伤变量D为1。对表3中的数据进行处理分析,拟合曲线如图21所示。岩石的细观损伤变量随应变的变化趋势,也大致分为2个阶段:第1阶段为损伤平缓增长段,应变从0增加到0.005 0的过程中,岩石几乎无损伤产生,直到应变到0.008 3时,砂岩试样的损伤变量仅为0.076 38,损伤变量增加极小;第2阶段为损伤迅速增长段,在应变0.008 3后,砂岩试样的损伤变量迅速增加,应变从0.008 3增长到0.011 5,损伤变量从0.076 38迅速增长到1,占总应变量的93%左右。由以上分析,可知损伤变量随应变的增长呈指数增长,因此利用指数型函数对数据进行拟合,得到应变ε与细观损伤变量Dx之间的函数关系:
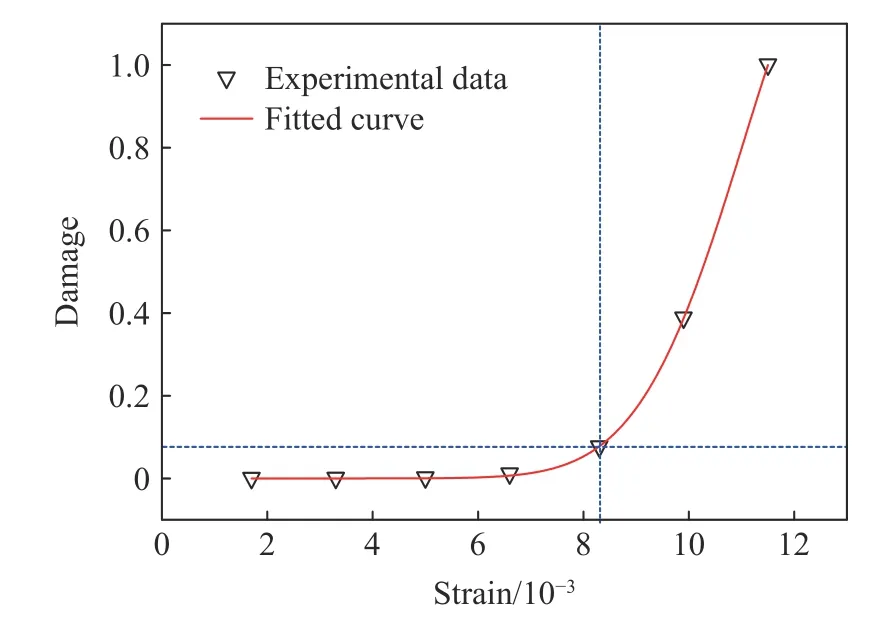
图21 CT扫描实验数据及其拟合曲线Fig.21 Experimental data and fitting curve of CT scanning
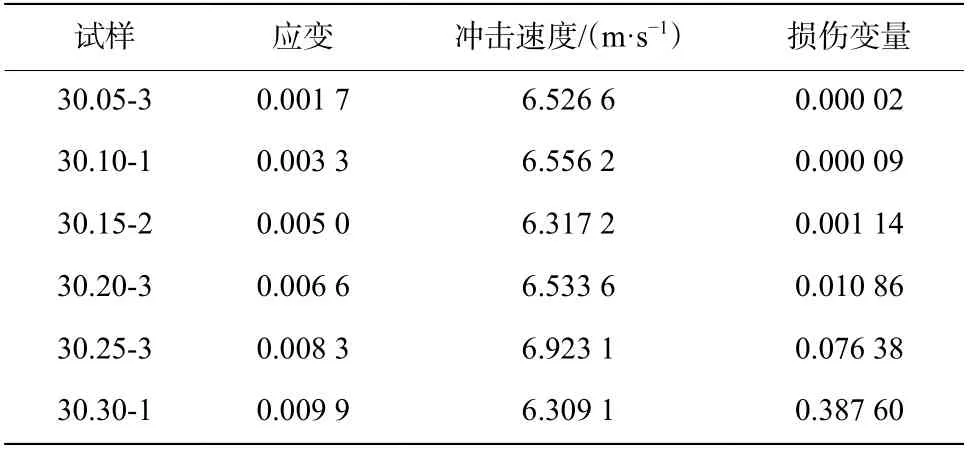
表3 CT扫描损伤测试结果Table3 CT scan damage experiment results
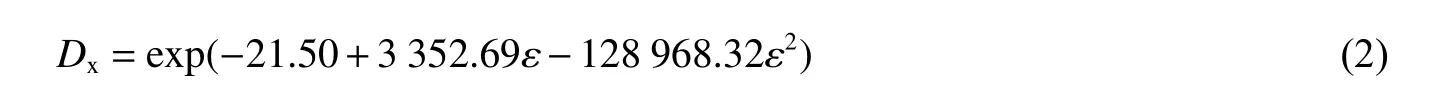
式中:Dx为砂岩的细观损伤变量,ε为砂岩在冲击荷载作用下的应变。
式(2)的拟合优度R2=0.999 98,拟合效果良好。通过此关系式,可以搭建起砂岩应变与细观损伤变量之间的定量关系式,通过应变参数便可以得到砂岩试样的细观损伤变量。相对其他损伤变量关系式,该关系式大大简化了损伤变量的求解过程。
式(1)~(2)分别从宏观和细观两方面得到了应变与损伤变量之间的定量关系式,其形式均符合指数函数形式D=exp(a+bε+cε2),但在表征砂岩试样损伤程度上稍有差异,具体表现为参数a、b、c不同。究其原因为:宏观损伤变量由声波波速实验测得,其原理为纵波沿试样轴向方向穿过损伤岩石,通过波速的衰减表征岩石的损伤程度,阻碍波速传播的主要因素为岩石的密度、内部孔隙、破坏形式等,宏观损伤变量Dh主要从整体上间接表征了岩石的破坏程度;细观损伤变量由CT扫描和数字岩心技术得到,其原理为以砂岩试样三维重构图为基础,利用Avizo 8.1软件对岩石内部的孔隙、裂纹和砂岩颗粒进行区分、提取和计算,最终得到损伤试样内部的裂纹密度,细观损伤变量Dx主要从损伤试样内部裂纹的体积占试样总体积的百分比表征岩石的破坏程度。宏观和细观损伤变量在表征岩石损伤程度时所用原理不同,因此式(1)~(2)在表征砂岩试样损伤程度上稍有差异,在具体应用中可根据其检测手段和原理,对式(1)~(2)进行选择。
由图17、21可以看出,宏观损伤变量Dh和细观损伤变量Dx随应变ε的变化趋势基本一致,在冲击荷载作用下砂岩试样的损伤变量D随应变ε的增加并不是简单的线性增加,而是当应变ε逐渐增加累积到一定数值时,损伤变量突然大幅度增加,损伤变量D随应变ε增加过程中存在着明显的应变损伤阈值,即εt=0.008 3。砂岩试样在冲击变形过程中,应变处于损伤阈值εt前,其损伤变量D增长较平缓,一旦达到应变损伤阈值εt,继续增加应变ε,砂岩的损伤变量D便会急剧增加。
4 结 论
利用带有应变控制环的SHPB实验系统,对砂岩试样进行控制应变条件下的动态冲击实验,结合波速测试和CT扫描,对砂岩试样的破坏过程、破坏机理和损伤演化规律进行研究,得到了以下主要结论。
(1)在冲击荷载作用下,砂岩试样整体呈现近似双锥形的破坏形式,在整个动态破坏过程中,由于受端部摩擦效应的影响,砂岩试样先将发生剪切破坏,紧随发生压缩破坏,其整体破坏模式为剪切-张拉混合破坏。
(2)砂岩试样在动态破坏过程中,裂纹的产生及扩展大致分为3个阶段:无裂纹阶段(应变0~0.003 3)、微裂纹起裂阶段(应变0.003 3~0.008 3)和裂纹贯通阶段(应变0.008 3~0.009 9),主要裂隙为偏内部的环向裂纹和外围圈的径向裂纹,且裂纹集中区域主要分布在试样中间外围。
(3)宏观和细观损伤演化规律研究均表明,损伤变量随应变呈指数型增长,其形式均符合指数函数形式D=exp(a+bε+cε2),利用曲线拟合方法,分别建立了基于应变参数的损伤演化定量关系式。
(4)砂岩试样的损伤变量随应变的增长趋势大致分为两个阶段:第1阶段为损伤平缓增长区(应变0~0.008 3),该阶段内砂岩试样无明显的破坏状态;第2阶段为损伤迅速增长区(应变0.008 3~0.011 5),该阶段砂岩试样迅速发生整体破坏;破坏过程存在明显的应变损伤阈值(0.008 3)。该结论可为爆破工程中砂岩变形的安全控制提供参考。

