黏弹性固体中地下爆炸辐射地震波能量的演化*
卢 强,丁 洋,刘赟哲,唐仕英,郭志昀,王占江
(西北核技术研究所,陕西 西安 710024)
研究地下封闭爆炸时通常把爆炸源简化为球形爆源,这样地下爆炸问题可简化为球面波问题。地下爆炸能量与源区介质发生强烈的耦合,最终以波的形式向周围介质辐射地震波能量。为表征地下爆炸或地震激发的震源强度,学术界提出了多种模型[1-3]。
根据Mueller等[4-5]提出的二阶震源模型,地下爆炸震源可用作用在弹性半径上的稳态压力叠加一个指数衰减的动态压力组成。在地下爆炸地震效应研究中,一般用折合位移势 ψ (τ) 或折合速度势 γ (τ)的振幅谱表征震源强度[6],折合位移势稳态值 ψ∞和爆后介质弹性半径处的稳态压力(也称准静态压力)呈线性关系。同时,折合位移势稳态值 ψ∞还 可以和地震学中反映源区不可恢复非弹性形变的地震矩M0联系起来。结合Murphy[7]给出M0∝ψ∞的 线性经验公式,则爆后弹性半径处的稳态压力和地震矩M0也呈线性关系。在研究波传播路径上的震动效应时,地下爆炸空腔中的准静态压力和动态压力对震动效应都有贡献,仅用和准静态压力相关的地震矩或折合位移势稳态值表征地下爆炸震源强度是不完备的,不能全面反映爆炸空腔内动态压力在地介质内引起的震动效应。
Choy等[2]和Boatwright等[3]利用大量的地震事件,基于能量的概念建立了地震波能量和能量震级之间的关系,以此表征震源强度。袁乃荣等[8]和李赞等[9]利用国家地震台网和全球地震台网的宽频地震波数据对地震波的能量震级进行研究,指出地震波对传播路径区域造成的破坏直接与地震释放的地震波能量相关,可见地下爆炸向介质中耦合的地震波能量是表征地下爆炸震源强度的另外一个重要参数。
为研究地下爆炸与介质的能量耦合效应,Sanchidriár等[10]利用多次野外岩石爆破,结合地震仪记录图、高速摄像机拍摄的岩石爆破面的运动速度以及爆破后岩石碎块尺寸的分布等实验结果,从地震波能量、动能、断裂能等方面研究了爆炸能量的组成。田振农等[11]以块体离散元计算方法为基础,研究了岩体中爆腔内的压力脉动及爆炸能量分布特征,指出爆源近区岩体结构性质对爆腔内压力脉动规律影响不大,爆腔内压力峰值与炸药量无关,给出了岩石断裂破坏消耗能量、变形能、用于抛掷的能量的比例。郭家豪等[12]基于反映高程放大的质点振动公式建立了侵彻钻地弹爆炸地震震源能量的计算模型,并结合经验公式推算爆炸总能量,从而评估钻地弹威力。吴亮等[13]对耦合装药条件下柱状炸药爆炸的能量分布进行了研究,分析了爆炸能量和岩石介质的耦合机制,计算给出了爆炸能量与介质耦合过程中不同力学过程的能量占比。肖卫国等[14]基于地下爆炸试验实测的地表速度,以折合速度势低频稳态值(即折合位移稳态值)表示的地震耦合强度,研究了黄土、砂砾石和花岗岩场地地下爆炸的地震耦合效应,指出对于相同当量、相当比例埋深下的地下爆炸,地震耦合强度和源区介质特性有着强烈的依赖关系。
本文中,利用广义Maxwell黏弹性体中球面波Laplace域的解,反演计算黄土中地下爆炸的速度场、位移场、应力场和应变场,以任意两个不同半径处球面之间区域作为观测区域,建立地下爆炸自由场辐射地震波能量的计算方法,分析地震波能量的传播演化规律,相关结果对于理解地下爆炸地震波能量在黏弹性介质中的衰减规律以及分析地下爆炸中实测的自由场数据具有一定参考作用。
1 地下爆炸黏弹性区辐射能量的组成
球面波条件下,某个半径r的球面上,其径向应力为 σr(r,t),则径向面力Fr(r,t) 可以表示为 4 πr2σr(r,t)。球面波下材料仅有径向位移ur,则面力在径向位移上的做功W可以写为[10]:
式中:vr为径向粒子速度,r为爆心距。
力Fr(r,t)在 半径r的球面上做的功W(r,t) 即 是流入此球面的总能量。根据能量守恒,能量流经r0≤r≤r1的区域时,流入能量W(r0,t) 转化为此区域内所有质点的动能Ek(r0,r1,t)(即辐射动能)、介质应变能(也称内能或势能)Ep(r0,r1,t) 、材料耗散能Ed(r0,r1,t) 以及从半径r1的 球面上流出的能量W(r1,t),如图1所示。则有:

图1 黏弹性固体中爆炸地震波能量的组成Fig.1 The composition of the energy of explosion seismic wave in visco-elastic solids
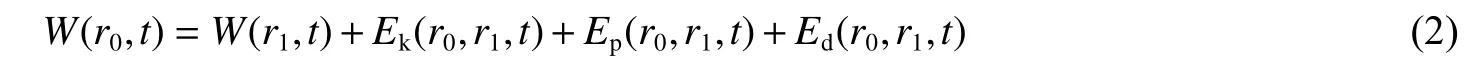
式中:Ek(r0,r1,t)和Ep(r0,r1,t) 分别为t时刻整个区域r0≤r≤r1内所有质点动能和应变能密度函数的空间积分,则有:

式中: ρ 为材料密度, εr为径向应变, εθ为切向应变, σθ为切向应力。
式(2)是基于能量守恒获得的,适用于任意固体中球面波能量传播演化的分析。若要求解球面波能量流经r0≤r≤r1的 区域时材料的耗散能Ed(r0,r1,t),则有:
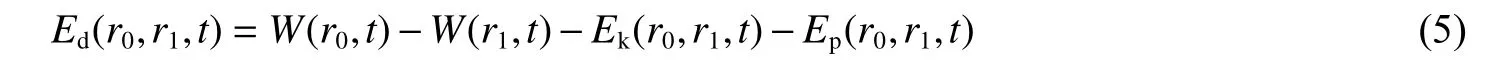
考虑t→∞ 的特殊情况,此时波完全离开r0≤r≤r1区域,则此区域内质点动能Ek(r0,r1,∞)=0 。按照黏弹性球面波的解,式(4)可以写为[15-16]:

式中: σ0s为稳态空腔压力,Ge为黏弹性材料的静态剪切模量。从式(6)可以看出,稳态空腔压力 σ0s形成的势能主要分布在几倍空腔半径的范围内,比如当r1=10r0时,此观测区域储存了99.9%的势能。
由式(3)~(6)可给出球面波能量流经r0≤r≤r1的 区域时材料的耗散能Ed(r0,r1,∞),有:
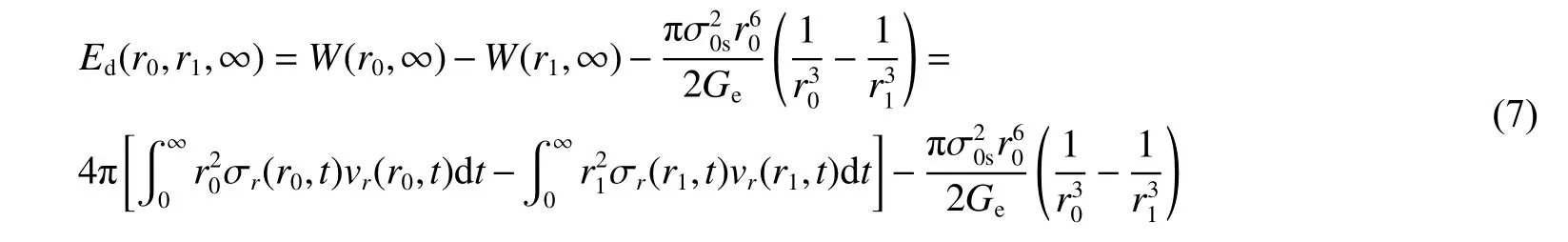
2 黏弹性固体中地下爆炸辐射地震波场的计算方法
根据无限介质中黏弹性球面波理论,在Laplace域,以波传播系数表征的黏弹性球面波粒子速度(r,s)、粒子位移(r,s)、径向应力(r,s)、切向应力(r,s)、径向应变(r,s)、切向应变(r,s)可写为[15-16]:

式中: µ 为材料的泊松比,s为Laplace变量, β(s)和(r0,s) 分别为波传播系数和弹性半径为r0的球腔上压力边界条件的Laplace表示。
由式(8)~(13)可知,若 ρ 、r0、 µ 、 β(s)和(r0,s) 已知,则方程组完备。下面确定波传播系数 β(s)和弹性空腔半径上的压力边界条件(r0,s)。广义Maxwell黏弹性模型可以用多个Maxwell体并联描述,如图2所示,其Laplace域表示可写为[15]:
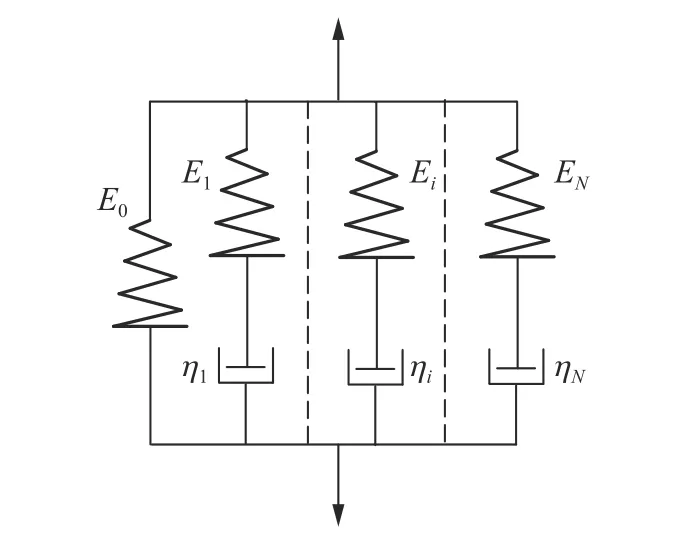
图2 广义Maxwell体模型Fig.2 The generalized Maxwell element model

式中: θi=ηi/Ei、ηi和Ei(i=0,1,2,···,N)分别表示第i个Maxwell体松弛时间、黏度系数和弹性模量,(s) 为Laplace域的弹性模量,弹性元件的弹性模量E0、松弛时间θ0=∞ 。
波传播系数 β(s)和E(s)之间满足[17]:

Muller等[4-5]通过对地下爆炸自由场测量结果的分析,认为球腔上压力边界条件的(r0,s)可写为:
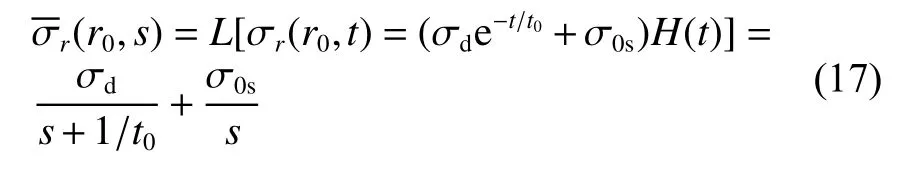
式 中: σd为 动 态 压 力 峰 值,σ0s为 稳 态 空 腔 压 力,σd+σ0s为空腔压力峰值,t0为压力衰减的时间常数,H(t) 为 亥维赛阶跃函数(Heaviside function),L表示Laplace算符。
至此,把式(16)~(17)代入式(8)~(13),即可给出黏弹性球面波各参数的Laplace域的形式;通过对式(8)~(13)进行Laplace逆变换,即可求解出时域的粒子速度vr(r,t) 、粒子位移、ur(r,t) 径向应力σr(r,t) 、切向应力σθ(r,t) 、径向应变εr(r,t)、切向应变εθ(r,t) ;把这些时域的解代入式(1)~(5),即可给出某个观测区域r0≤r≤r1地下爆炸的辐射能量。
3 地下爆炸辐射地震波能量的计算实例
以黄土中空腔爆炸为例说明地下爆炸辐射地震波能量的特征。参照文献[16],取空腔半径为0.025 m,空腔边界压力为 σr0=−(e−t/t0+1) MPa,其中t0=θ1。地震波的观测区域分别为r0=0.025 m,r1=0.096 5,0.146 5,0.200 0 m,黄土黏弹性参数见表1。

表1 黄土黏弹性参数[18]Table1 The visco-elastic parameters of loess[18]
图3给出黄土中地下爆炸辐射地震波能量的传播演化。对于某个特定的r0和r1,在r0≤r≤r1的观测区域内,r0边界上流入的能量最终趋于稳定值W(r0,∞) ;在r1边界上,当波到达此处,能量开始流出,最终趋于稳定值W(r1,∞) ;自r0边界上开始流入能量后,势能Ep(r0,r1,t) 和动能Ek(r0,r1,t)即逐渐增加,当波开始流出r1边界时,Ep(r0,r1,t)和Ek(r0,r1,t) 突然减少,最终Ep(r0,r1,t) 趋于稳定值(如式(6)),Ek(r0,r1,t)趋于0,Ek(r0,r1,t) 为0时说明波已完整地从r0≤r≤r1观测区域离开;自r0边界上开始流入能量后,Ed(r0,r1,t)即逐渐增加,最终趋于稳定值Ed(r0,r1,∞)。Ep(r0,r1,∞)和Ed(r0,r1,∞) 分别表示波完整通过r0≤r≤r1区域后留在该区域介质的势能和材料吸收的耗散能。

图3 黄土中地下爆炸辐射地震波能量随观测区域的变化Fig.3 The variation of the energy of the radiated seismic wave from underground explosion in loess with the observation region
当观测区域变大后,比如r0不变,随着r1由0.096 5 m增大至0.2 m,r1边界上流出的能量W(r1,∞)越来越低;势能Ep(r0,r1,t) 、动能Ek(r0,r1,t) 和耗散能Ed(r0,r1,t)在观测区域重合的部分其变化曲线也是重合的,观测区域越大则获得的能量传播信息越多;Ed(r0,r1,t) 随着观测区域的变大,Ed(r0,r1,∞)随之增大。
在地下爆炸实验研究中,一般是通过测量不同爆心距处粒子速度、应力等参量表征应力波的传播特性[7,19-22],而地下爆炸辐射的地震波能量不能直接进行测量,但可以通过测得的粒子速度、应力等物理量计算。比如,通过同时测量某球面处径向应力和径向粒子速度波形,计算得到该球面处流入能量W(r,t);通过测量r0≤r≤r1区域内不同位置的有限个粒子速度波形,利用一定的物理和数学处理方法[23],获得该区域的粒子速度场,从而可由式(3)计算得到Ek(r0,r1,t) ;通过测量r0≤r≤r1区域内不同位置有限个径向应力、切向应力和径向粒子速度波形,结合一定的物理和数学处理方法构造径向应力 σr(r,t)、切向应力σθ(r,t) 、径 向 应 变εr(r,t) 和 切 向 应 变εθ(r,t) 的 场,从 而 利 用 式(4)计 算 得 到Ep(r0,r1,t) ;在 获 得W(r,t)、Ek(r0,r1,t)、Ep(r0,r1,t) 之后,即可求得耗散能Ed(r0,r1,t)。
4 地下爆炸辐射地震波能量的传播特征
4.1 不同球面处流入能量的传播特征
为研究黏弹性固体中地下爆炸在不同球面处流入能量的传播特征,把观测区域取为r=0.025~10 m。图4给出黄土中不同半径球面处最终流入能量W(r,∞) 的变化。可看出,W(r,∞) 随半径r增加而减小,并呈现出不同的变化规律。结合数据的变化特点,人为把0.025~10 m的空间范围划分为4个区域,并分段对W(r,∞)进行拟合。可以发现,在图中R1、R3、R4区域可近似用幂函数进行拟合,而在R2区域用指数函数拟合更符合W(r,∞)的变化规律。若用R1~R4这4个区域数据的拟合公式分别反推空腔壁上的能量参数,则预估的能量分别为真实输入能量的0.93、0.60、189、2.71倍,可见若用某局部观测区域的实测数据预估源区或远区波动参数时仍需慎重。
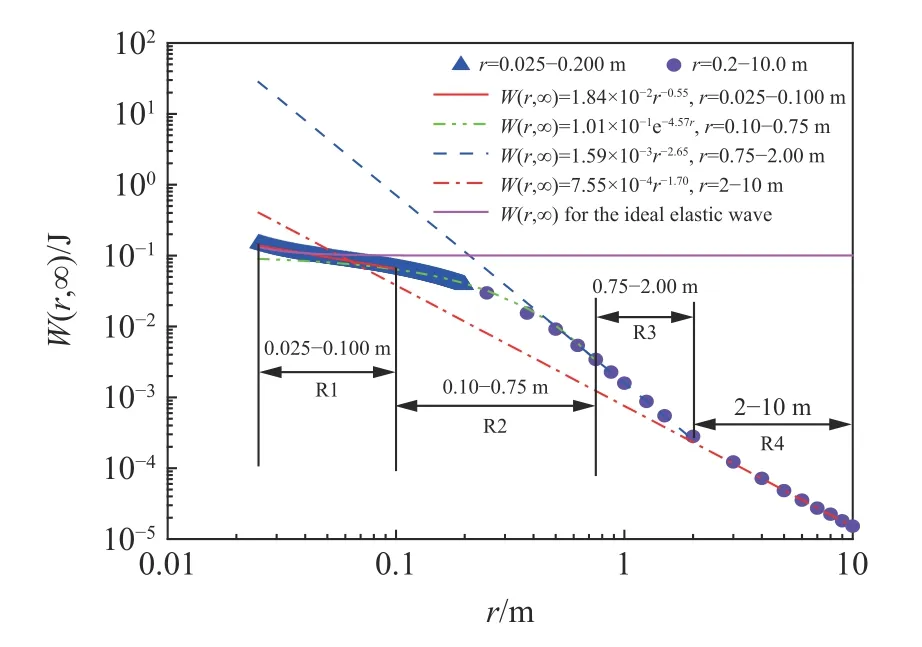
图4 黄土不同半径球面处最终流入能量W (r,∞)的变化Fig.4 The changes in the inflow energyW (r,∞)at different radii of the sphere in loess
在无黏性的理想弹性固体中,其耗散能为零,则可通过式(7)得到理想弹性材料中地下爆炸不同球面处流入能量:
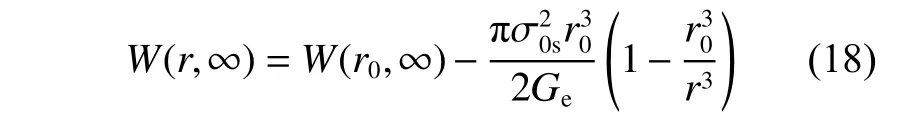
图4同时给出了不考虑介质黏性时W(r,∞)的传播图像,可看出,理想弹性固体中不同球面处流入的能量随着波传播距离的增加而逐渐降低,并在传播至几倍空腔半径处即基本保持不变。可见,黏弹性材料中地下爆炸在不同球面处流入能量的传播特征要比理性弹性材料复杂的多。
4.2 地震波辐射动能的传播特征
由公式(3)可知,为求得r0≤r≤r1区域内的辐 射 动 能Ek(r0,r1,t) ,需 先 求 得 此 区 域 内vr(r,t)的空间分布。按照第2节的方法,图5给出了黄土中不同时刻粒子速度vr(r,t)的空间分布。可以看出,当t=100 µs时,在空腔壁上激发的应力波还未完全进入观测区域,随着时间的增加,波阵面一直向远离爆心方向传播,同时波长逐渐增加、幅度逐渐降低;当t=300 µs时,在观测区域内可以观察到完整的应力波。
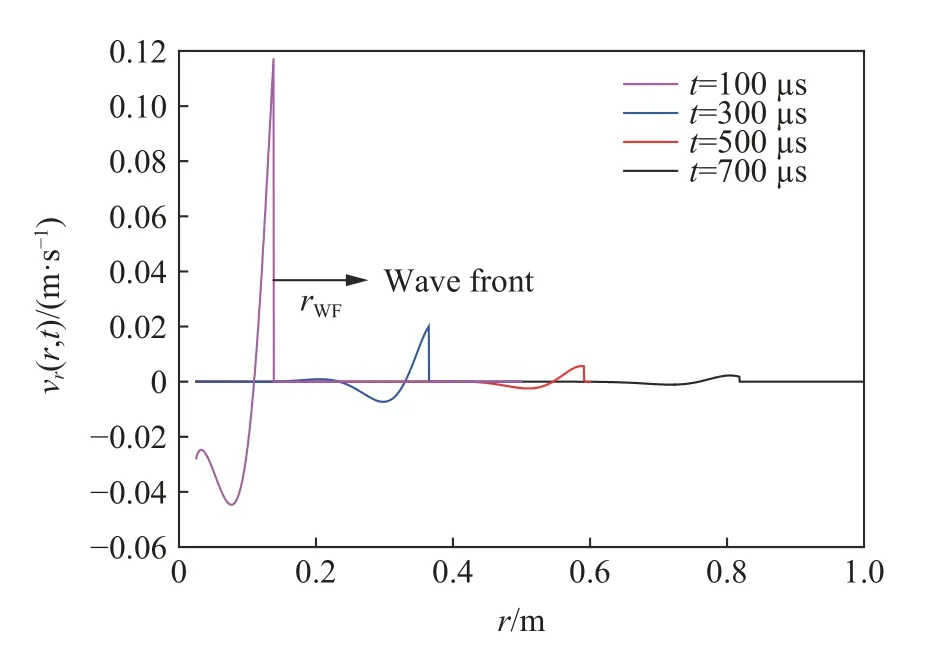
图5 黄土中不同时刻粒子速度的空间分布Fig.5 The spatial distribution of the particle velocity at different times in loess
利用式(3)计算给出不同时刻整个空间中总动能的空间分布,如图6所示,图中平台对应的即是地震波辐射动能稳态值Ek。当在观测区域内能观测到完整应力波时(取t=300~9 000 µs),把波阵面对应位置rWF设为横坐标、地震波辐射动能稳态值Ek设为纵坐标,则可以给出地震波辐射动能稳态值Ek随波前位置rWF的变化曲线,如图7所示。与W(r,∞) 类似,在能观测到完整应力波空间分布的区域内,地震波辐射动能稳态值Ek随着波传播距离rWF的增加而减少。结合数据变化特征,在离爆心较近的区域,地震波辐射动能稳态值随波前位置的变化曲线可近似用指数函数拟合,而在较远区域,可用分段幂函数进行拟合。
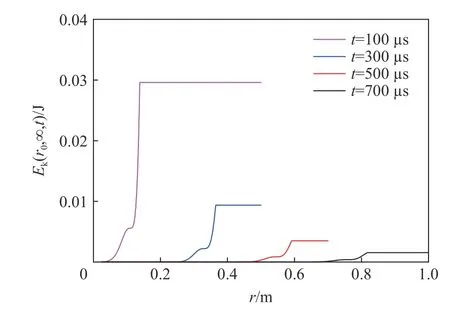
图 6 黄土中不同时刻辐射动能的空间分布Fig.6 The spatial distribution of the radiated kinetic energy at different times in loess
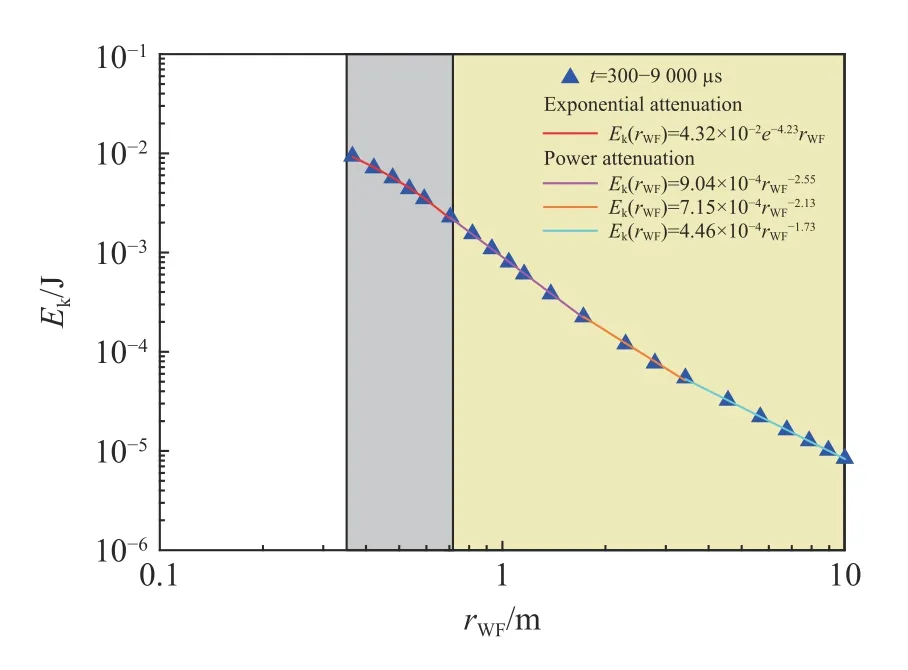
图7 黄土中地震波辐射动能随波前位置的变化Fig.7 The variation of the radiated kinetic energy of seismic wave with the position of wave front in loess
5 结 论
由上述分析得到以下几点结论:
(1)利用建立的黏弹性固体中地下爆炸辐射地震波场的计算方法,给出了地下爆炸有限黏弹性观测区域中流入(出)能量、动能、应变能、耗散能的结果,数值计算结果和理论分析结果相符,说明本文计算方法的正确性。
(2)在黏弹性介质中,某球面处流入的能量W(r,∞)随半径增加而逐渐降低,同时呈现出复杂的衰减规律,大部分区域W(r,∞) 的 衰减规律可用幂函数拟合,而部分区域W(r,∞)的衰减更符合指数函数衰减特征;在理想弹性介质中,W(r,∞)在几倍弹性半径外即可稳定到某一定值。
(3)在某一固定的有限观测区域内,当观测时间足够长时,势能和耗散能均趋于某一定值,辐射动能趋于零。
(4)当有限的观测区域能完整地容纳地震波时,利用粒子速度的空间分布可以计算给出此时地震波辐射动能的空间分布,地震波辐射动能的稳态值随波传播距离的增加而减少,且衰减规律比较复杂,总体上可以用指数函数和幂函数进行分段拟合。

