一种强耦合预估-校正浸入边界法*

张和涛，宁建国，许香照，马天宝

（北京理工大学爆炸科学与技术国家重点实验室，北京 100081）

计算力学领域中的流固耦合问题具有广阔的应用背景，长期以来吸引着众多研究者关注。流固耦合仿真的理论和数值模拟一直是计算力学领域中难度较大的课题之一。浸入边界法由Peskin[1-2]于1972年首次提出，目前已发展成为流固耦合数值模拟中广泛采用的一类方法[3]，被应用于研究声场[4-6]、涡激振动[7-10]、纳米流体[11]、湍流[12]等复杂问题。典型的浸入边界法采用独立的拉格朗日网格描述固体结构并将之嵌入欧拉网格描述的流场中。通过对边界附近进行特殊处理，浸入边界法确保了流固耦合边界上的无滑移条件和力平衡关系得以满足。

浸入边界法的一个分支是锐利浸入边界法[13]。锐利浸入边界法严格保持边界位置上的强间断，根据边界两侧的应力推断相互作用能够始终维持锐利边界。借助于边界单元的特殊处理规则，锐利浸入边界法通常无需在流体Navier-Stokes方程中添加附加源项，因此对格式稳定性影响较小，有利于推广到可压缩流体情形。理论上，锐利浸入边界法可以具有高阶精度[14]，在模拟高雷诺数流动时相比浸入边界法的另一分支模糊浸入边界法[15-16]具有优势。锐利浸入边界法的核心问题是处理被边界截断的单元，简称截断单元（cut-cell）。主流实现方式分为两类：虚拟网格法（ghost-cell method）[17-28]和截断单元法（cutcell method）[29-33]，其中应用相对较多的是虚拟网格法。对虚拟网格法的研究表明，为了处理截断单元，虚拟网格法需要进行多维重构，常用方法包括形函数插值和移动最小二乘法等。

虚拟网格法存在的一个问题是当耦合边界在流体的固定网格上移动时不能维持严格的质量守恒[23]。边界运动时会改变固体的覆盖域，在流体网格上产生许多失效单元和新增单元。被更新后的固体覆盖的失效单元会损失其中包含的所有信息并造成失效单元质量丢失。为了获得正确的压力，虚拟网格法有时需要对新增单元进行填充，导致新增单元获得额外质量。因此整体上虚拟网格法不能维持质量守恒。Seo等[34]的研究确认违反几何守恒律及相应的质量损失是造成虚假振荡的首要原因，并提出了一种针对不可压缩流体的改善方案。目前对可压缩流体仍无合适的解决方法。

截断单元法考虑了截断单元体积变化的过程，因此通过合适的单元处理可以实现精确的质量守恒。Monasse等[31]提出了一种针对可压缩流体和刚体耦合的守恒型浸入边界法，通过校正Godunov通量来还原损失的质量，但由于采用了有限体积法，涉及截断单元的几何计算会比较困难。与Monasse的方法类似，Sotiropoulos等[13]给出的结论表明，在截断单元法中对截断单元的拓扑管理是主要问题，妨碍了这一类方法推广到三维情形。Brady等[33]指出，当截断单元体积趋于零时会引起系统刚性问题。用有限差分法替代有限体积法可以显著简化截断单元的计算。然而由于有限体积法在计算流体力学领域的广泛应用，考虑有限体积法的耦合问题仍然是必要的。

为了克服虚拟网格法和截断单元法存在的困难，本文中，将提出一种区别于这两类方法的新思路，即适用于可压缩流体和结构耦合问题的强耦合预估-校正锐利浸入边界法。首先，分析虚拟网格浸入边界法导致质量不守恒的原因，揭示网格拓扑变化的影响。其次，阐述一般流固耦合系统的矩阵表示，导出强耦合Gauss-Seidel迭代格式，进一步导出预估-校正格式，基于该格式，提出预估-校正算法，预估步骤使用无耦合边界的流体模型求解，并对流体施加校正。然后，介绍独立的介质求解器，并详细阐述校正步骤，在校正步骤中，通过一组输运规则来实现输运过程，保证质量守恒。最后，使用该方法测试若干数值算例，检验该方法的准确性和收敛性。

1 虚拟网格法

有限体积法在重构流场的通量函数时需要使用相邻多个单元组成的模板。当通量模板包含至少一个截断单元时，一般采取构造虚拟网格的方式补全模板。一种常用的方法是使用基于移动最小二乘法的虚拟网格法补全模板。如图1所示，下方的4个单元组成一个通量模板。单元G被浸入的固体网格覆盖。斜实线代表浸入边界。点G关于浸入边界的镜像为点I，两点连线与浸入边界相交于点H。距点I一定半径范围内的单元组成一个支撑域 ΩI。在 ΩI上使用径向基函数移动最小二乘法拟合点I的物理量。

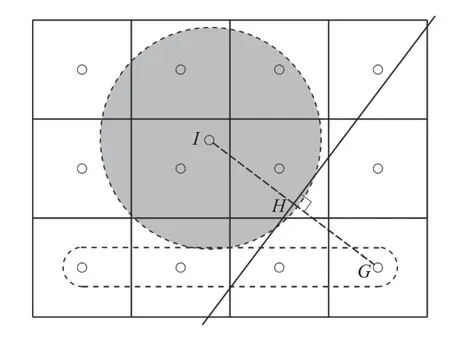
图1 根据镜像点I构造虚拟网格结点GFig.1 Construct the ghost pointGbased on its image pointI

根据点I的物理量和浸入边界上的边界条件可构造虚拟结点G。为了与固定边界情形下的边界条件一致，假设I和G关于H参考系满足固壁边界条件,可表达为：

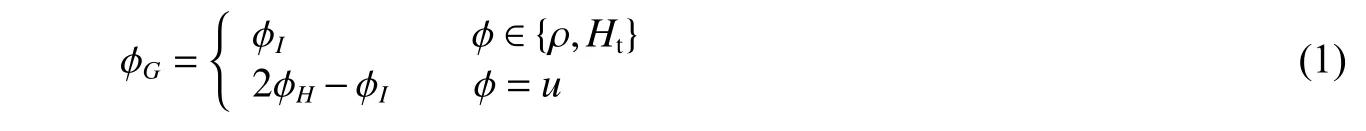
式中： ρ 为密度，Ht为总能，u为速度。该边界条件的两种情形分别对应于Dirichlet边界条件和Neumann边界条件。

虚拟网格法会导致流体质量的改变。如图2所示，当浸入边界在固定的欧拉网格上移动时，会覆盖一部分网格从而造成失效单元，同时一部分网格不再被覆盖而成为新增单元。虚拟网格法在构造虚拟网格时没有考虑到网格拓扑变化的影响。当出现失效单元时，网格拓扑发生突变，与连续的边界条件产生矛盾。虽然施加了边界条件，但是仍然会损失一部分质量。当出现新增单元时，为了拟合的光滑性，可能需要使用拟合方法对新增单元进行填充。同样地，在新增单元上的拟合算法中加入边界条件约束也不能保证质量守恒。

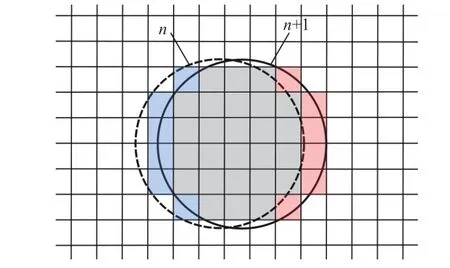
图2 从tn 时刻到tn+1时刻边界进行移动，造成红色的失效单元和蓝色的新增单元Fig.2 Boundary motion on a fixed grid from timetntotn+1.Dead(red)and fresh(blue)cells are generated by the motion

因此，设计质量守恒的锐利浸入边界法时，应当充分考虑网格拓扑的变化对流场的影响。与虚拟网格法不同，截断单元法可以实时计算网格变化，消除了质量损失，但也造成了算法实现上的困难。在第2节至第4节中，将推导一个预估-校正格式，基于该格式和网格拓扑变化构造一个质量守恒且易于实现的锐利浸入边界法。

2 强耦合预估-校正格式

2.1 流固耦合系统

一般情况下的流固耦合系统可以用一组抽象的状态量描述：式中：S=S(t)和F=F(t)分别代表在t时刻固体和流体的一组状态量，V被称为流固耦合系统的状态向量。从tn时刻到tn+1时刻的系统演化过程可以视为对状态向量的一次映射。假设流固耦合系统状态向量的所有映射均属于某个向量空间，且均存在唯一的逆映射。记x为向量， ϕ 为映射。为了描述方便，使用符号◦表示将映射作用于向量，约定如下记法：（1） ϕ ◦x=ϕ(x) ；（2） ϕ2◦ϕ1◦x=ϕ2(ϕ1(x))。注意两个映射之间不一定满足交换律，即 ϕ2◦ϕ1◦x≠ϕ1◦ϕ2◦x。

假定流固耦合系统从tn时刻到tn+1时 刻遵从某个映射。记该映射为 Φ ，那么系统演化可表示为：

记逆映射Ψ =Φ−1，则：

写成分块矩阵形式：

可进一步对矩阵作LDU分解：

其中：

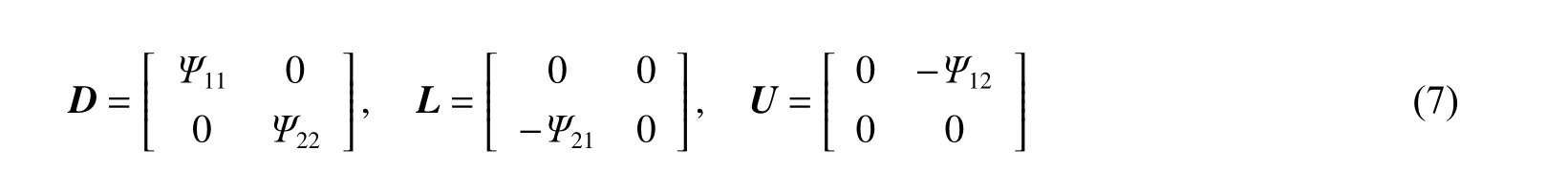
类比线性代数方程组，我们可以构造迭代格式。下面给出流固耦合系统的Gauss-Seidel迭代格式。

2.2 Gauss-Seidel格式

式(4)的Gauss-Seidel格式可表示为：

其中：

其中E为(D−L)的左逆，满足：

其中I代表对角线元素均为恒等映射的单位矩阵。易得：

则：

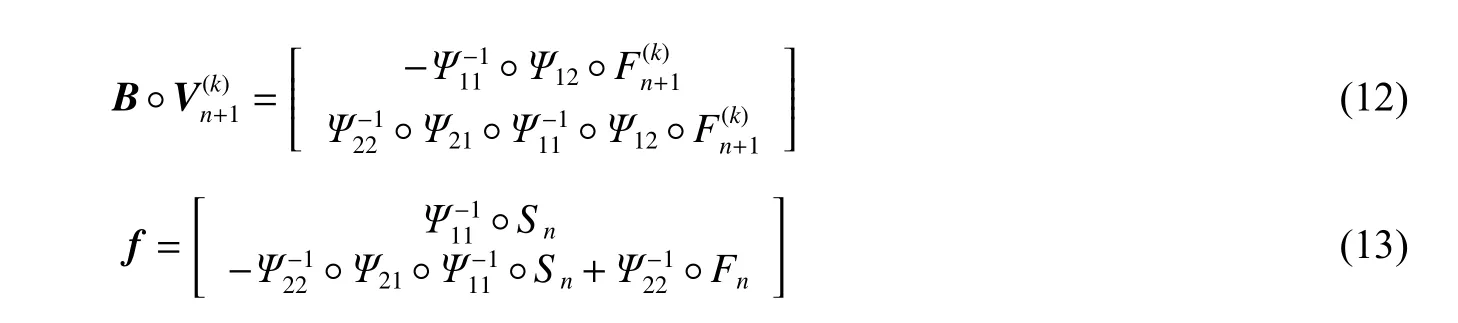
于是有：

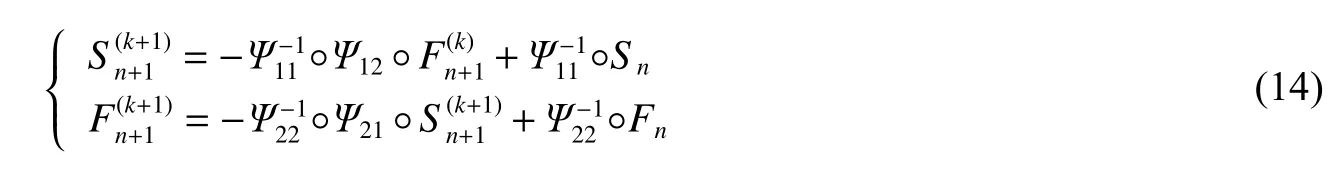
写成如下形式：

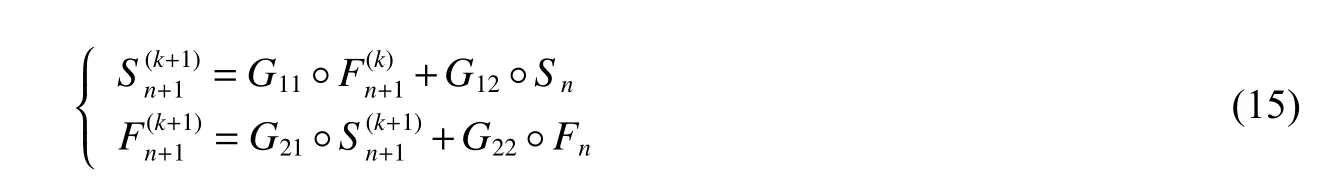
其中：

根据S和F的物理含义，可认为G12对应于固体求解器，代表固体对自身的贡献；G22对应于流体求解器，代表流体对自身的贡献；G11代 表浸入边界算法中的流体对固体的贡献；G21代表浸入边界算法中的固体对流体的贡献。

将式(15)整理为如下形式：

（1）给定迭代初始值，

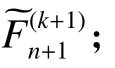
式(16)描述了一个强耦合的预估-校正算法流程。第3节中将依次阐述流体求解器和固体求解器，然后阐述浸入边界的耦合力算和流体的校正算法。

3 控制方程和离散格式

本节简要阐述流体和固体的控制方程与相应的离散格式。

3.1 流体控制方程和离散格式

二维黏性可压缩流体方程组为：

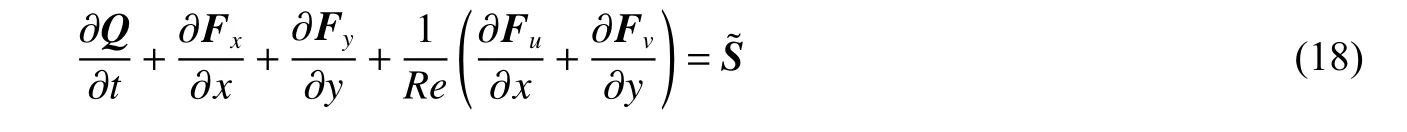
其中：

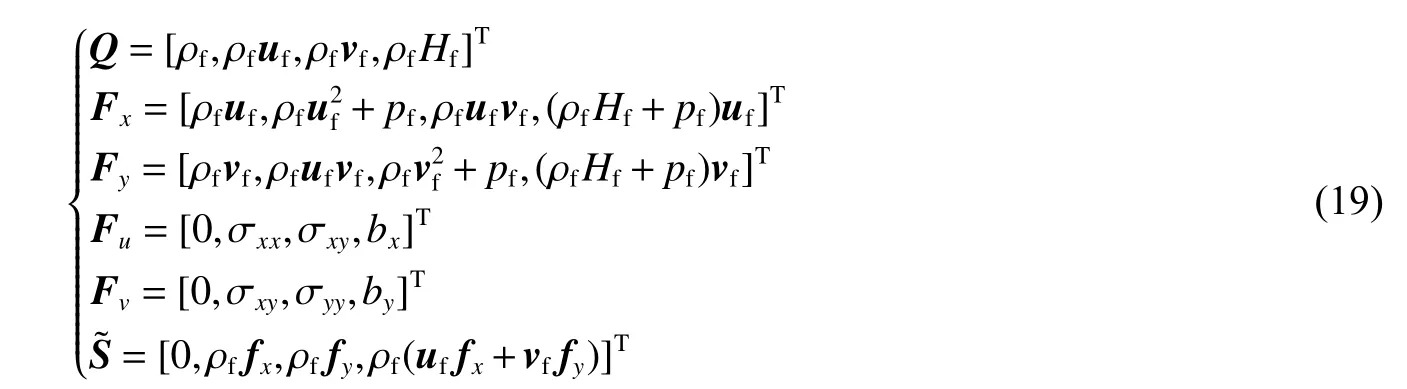
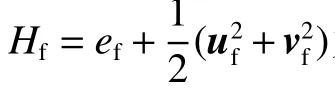
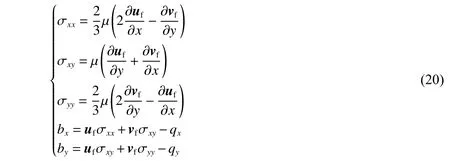
热通量qx和qy由 傅 里 叶定律给出：

式中： µ 为动力黏性系数；Pr为热传导系数；T=c2，c为声速； γ 为多方指数。

对于非黏性项，我们使用带有minmod限制器的二阶MUSCL[35]有限体积格式，通量F和G采用基于Zha-Bilgen分裂[36]的AUSM+-up[37]方法。对于黏性项则采取中心差分格式。最后使用三阶Runge-Kutta格式推进时间步。

3.2 固体控制方程和离散格式

3.2.1 刚体

刚体的Newton-Euler方程为：

式中：m为刚体质量；us为质心速度；fs为质心合力；fg为重力，在本文中均忽略重力影响；Is为质心惯性张量； ω 为角速度；Ts为质心合扭矩。

使用一阶的显式时间差分格式求解Newton-Euler方程，其中的合力和合扭矩来自流固界面上的耦合力。

3.2.2 线弹性体

线弹性体的控制方程及边界条件为：

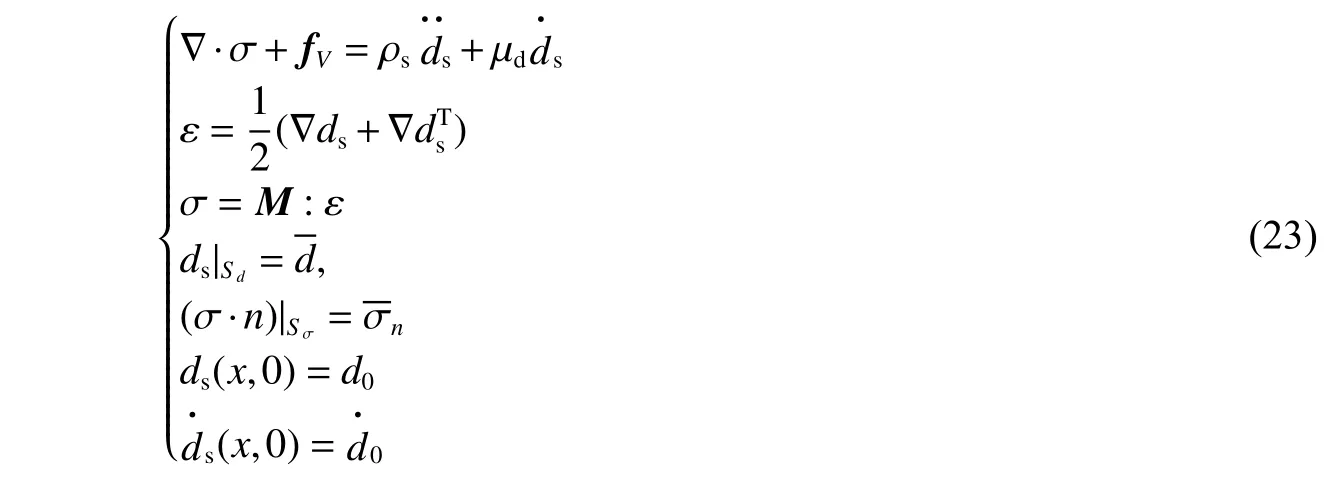
式中：σ为固体的应力；fV为体积力；ρs为固体密度；µd为阻尼系数，在本文中均假定µd=0；ds为位移；ε为应变；M为弹性矩阵；Sd和Sσ分别为位移边界和应力边界。

采取经典的有限元法对控制方程进行离散，并用Newmark-β隐式格式[38]推进时间步。

3.2.3 全局时间步长

计算流体的时间步长公式可以表示为：

式中：C为Courant数，l为网格最小尺寸，i为单元编号，ui和ci分别为单元i的速度和声速。对于固体，除了固体求解器本身限制的最大时间步长 ∆ts外，还必须考虑浸入边界在网格上移动引起的变化。一般限制单步之内浸入边界的移动不超过一个网格最小尺寸，故定义边界移动时间步长：

式中： Γ 代表浸入边界，常数Cb=0.95 。那么耦合场的全局时间步长为：

4 浸入边界算法

本节将具体阐述流体对浸入边界的耦合力算法和流体预估-校正算法中的边界处理方法，并解释算法保证质量守恒的原理。

4.1 耦合力

作用于固体表面的耦合力来自于流体的压力。假设流体的压力为p，浸入边界的外法向量（指向流体一侧）为n，在浸入边界 Γ 上对表面的压力积分可得到耦合力，即：

当 Γ 为直线段时，可采用高斯积分计算。关于高斯积分需要注意的是如果浸入边界的长度远大于流体网格尺寸，应先将浸入边界分割为若干小段以改善精度。同时，在选取高斯积分的积分点时，为了减小边界附近不光滑的压力分布造成的压力损失，可将积分点xΓ沿外法向量平移2h，即xΓ+2hn位置。

4.2 流体预估

式(17)中的预估步骤为：

式(28)对应的算法是将流体求解器应用于Fn。在式(28)中，固体的状态量S不影响Fn的演化，因此将流体求解器应用于Fn时，将流固耦合边界视为自由面，固体原本占据的空间初始化为零质量的单元，允许流体自由穿过耦合边界。

4.3 流体校正

4.3.1 基本思路

考虑一个浸入流体域的固体，其占据空间为 Ωs，边 界 为Γs。流 体 被 固 体 挤 占 一 部 分 空 间后，该部分空间的网格单元上的质量为零相当于真空。本文中，将这部分真空域记为 Ωv，边界为Γv。如图3所示，在tn时刻的真空域边界与固体域边界重合。在tn+1时刻二者分别演化为和，对应的内部空间为和。

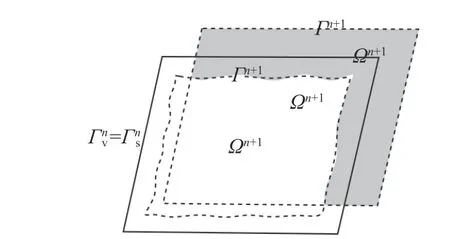
图3 流固耦合系统的子域变化（实线代表tn时刻的边界，虚线代表tn+1时刻的边界）Fig.3 Changes of the subdomains of the fluid-structure interaction system,where solid lines are boundaries attn ,and dashed lines are boundaries attn+1

4.3.2 输运算法

如图4所示，输运算法的第1个步骤是使用感染-免疫法[39]标记单元。为直观起见，用颜色代表不同标记。首先标记靠近浸入边界外侧的一层单元为蓝色，接着标记与蓝色单元相邻的位于内侧的一层单元为黄色，已标记的单元不再参与标记。以此类推，逐层向内染色。

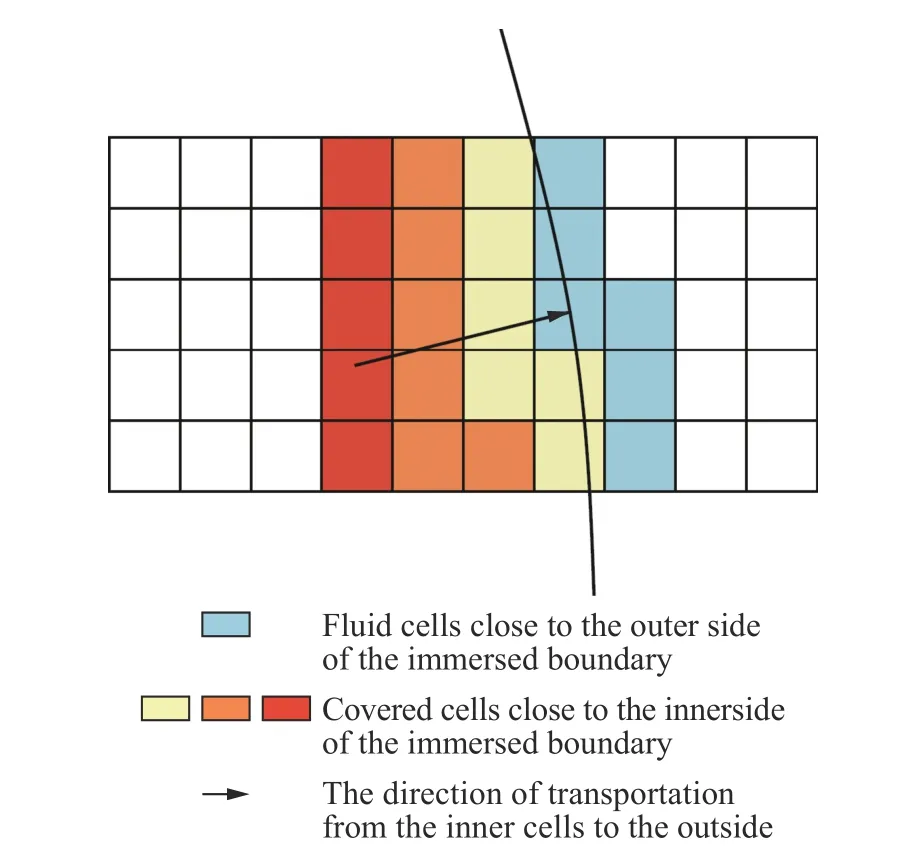
图4 流体标记和输运方向，曲线为浸入边界Fig.4 Fluid markers and direction of transportation,the curve is the immersed boundary

第2个步骤是根据染色顺序移动流体。考虑一个红色单元向橙色单元输运的过程。记单元的守恒量w=(ρ,ρu,ρHt)T。假设输运前红色单元的守恒量为wr，橙色单元的守恒量为wo。仅考虑均匀正交网格上的有限体积法格式，则输运导致单元的守恒量变为：

式中： λ 为输运比例系数。假设该红色单元周围存在n个相邻的橙色单元，其中n1个单元与该单元共享一条边，称为正相邻单元，n−n1个单元与该单元共享一个顶点，称为斜相邻单元。进一步假设输运比例与距离成反比，则在均匀正交网格上正相邻单元和斜相邻单元的输运比例系数分别为：

输运后红色单元的守恒量变为零。以此类推，按照染色顺序依次将流体从内侧单元输运到外侧，直到内侧单元流体完全转移到蓝色单元中，如图5所示。图中曲线为浸入边界， λ1和 λ2为输运比例系数。

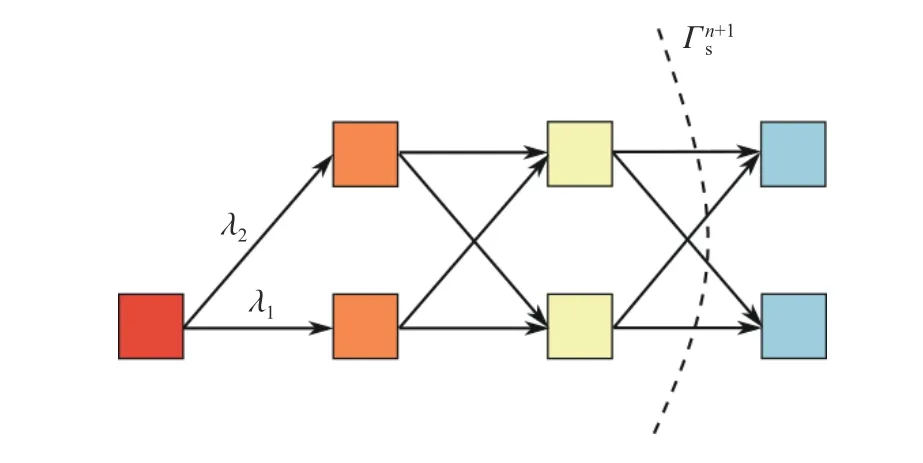
图5 依据染色顺序逐层输运流体Fig.5 Transport the fluid in sequence of colors

第3个步骤是校正蓝色单元的速度。单元的守恒量w与物理量( ρ,u,e)的域之间存在双射关系。假设当前蓝色单元的守恒量为，则唯一导出当前密度、速度和内能为：

式中：w为的第k个分量。假设蓝色单元的中心向浸入边界的投影位置为点B，记点B的速度为uB。根据无滑移条件，将蓝色单元的速度替换为点B的速度，保持密度和内能不变，重新导出守恒量：

至此，所有单元的校正结束。

上述的推导表明，该方法基于网格拓扑变化，无需构造虚拟网格。式(28)～(31)描述了校正步骤中的流体输运规则，本质上是守恒律和无滑移条件的应用，因此是一种严格保证质量守恒的方法。与同样保证质量守恒的截断单元法相比，该方法的第一个步骤中的标记操作仅需要获取网格单元与浸入边界的相对距离，无需计算截断单元的体积变化，简化了算法实现。

5 数值算例

5.1 一维活塞问题

为了考察方法的准确性和收敛性，对Monasse等[31]提出的一维活塞问题进行了数值模拟。假设沿x轴方向在[0,7]区间放置一个一维管道，并放置一个密度为2，长度为0.5的刚性活塞，其中心位于x=2处。在(2.25,5)内填充理想气体，密度为1，压力为1 05，速度为零，多方指数为1.4。在(0,1.75)∪(5,7)内填充相同的理想气体，密度和压力分别改为10和1 06。计算域两侧设定为周期边界条件。网格数N=1 440。

初始时刻气体和活塞速度均为零。两侧不平衡的气体压力推动活塞向右运动，产生向右的压缩波。利用移动最小二乘虚拟网格法和预估-校正方法分别计算，并与Monasse使用截断单元法的结果进行对比。图6展示了t=0.003时刻的压力分布曲线，表明3种方法计算结果较接近。虚拟网格法在左侧靠近浸入边界的压力和右侧波峰压力均偏高。预估-校正方法在左侧与截断单元法非常吻合，在右侧波峰则偏低一些。

图7展示了t=0.003之前的流体相对质量的变化。虚拟网格法计算的流场质量经历了先减少后增加的过程，并且由于网格拓扑的突变而产生了振荡。预估-校正方法计算的流场质量始终不变。通过对比，证明了预估-校正方法具有精确维持质量守恒的优势。

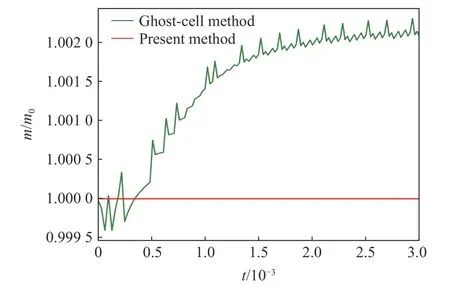
图7 流体相对质量的历史曲线Fig.7 History of the relative mass of the fluid

为检验收敛性，使用如下公式计算压力和速度分布的无量纲L2范数误差：

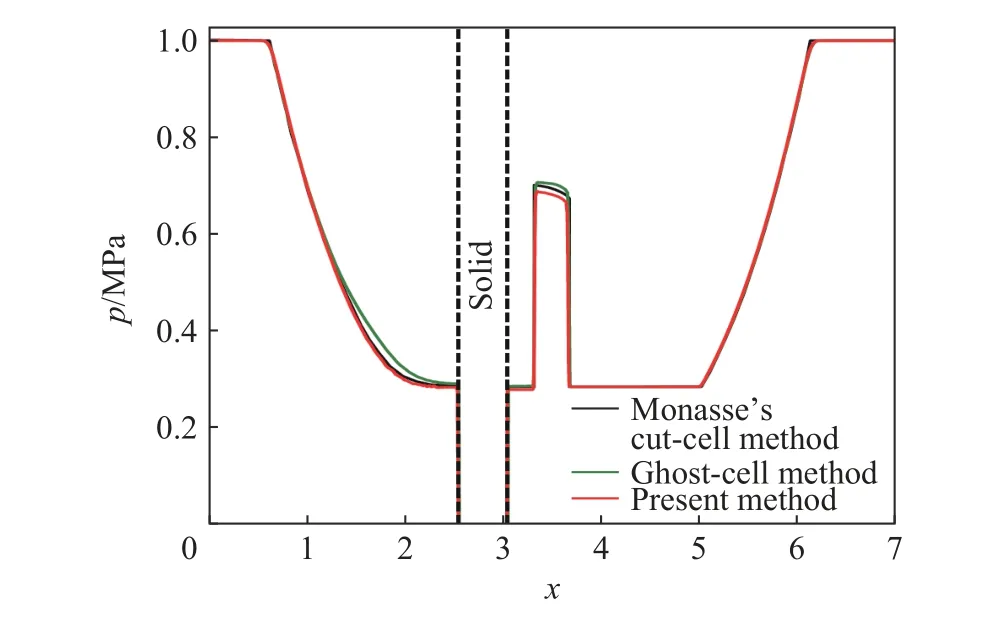
图6t=0.003时刻的压力分布（网格数为1 440，虚线表示浸入边界）Fig.6 Pressure distribution att=0.003(The number of cells is 1 440,and the dashed lines stand for the immersed boundaries.)

式中： ϕi为压力或速度，i表示分布曲线的数据点编号，为参考分布， ϕ0为 特征量。此处采用网格数N=7 290的计算结果作为参考分布，选取压力和速度的特征量分别为p0=106和u0=300 。图8展示了预估-校正方法计算的流体压力和速度的误差收敛曲线，证明压力和速度分布曲线关于流体网格数N呈一阶收敛。

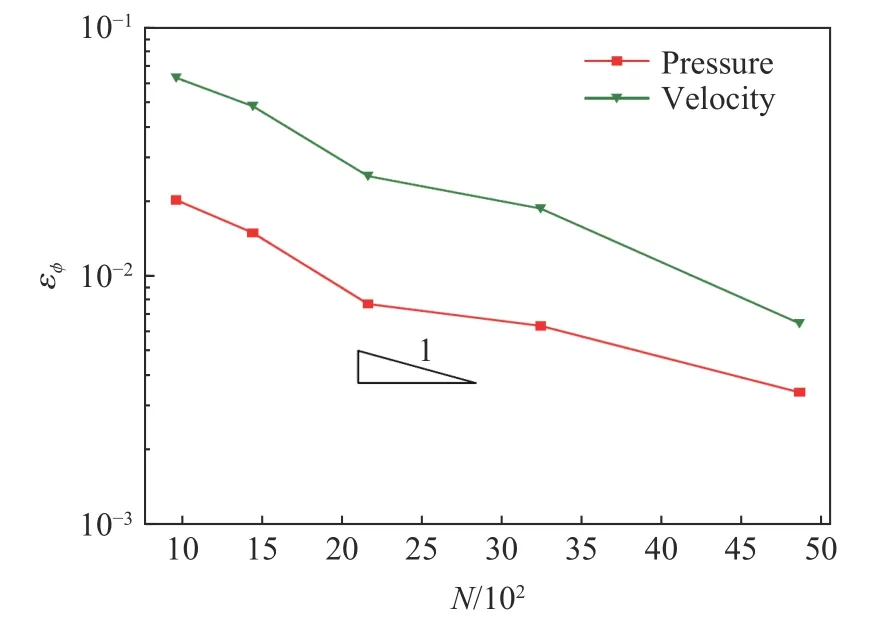
图8 压力和速度的无量纲L2范数误差Fig.8 Dimensionless L2 norms of error of the pressure and velocity

图9展示了预估-校正方法计算的流场密度关于时空坐标(x,t)的云图。图9中深蓝色条形区域代表活塞的历史轨迹，反映了活塞加速和减速的过程，与Monasse使用截断单元浸入边界法的计算结果也基本符合。

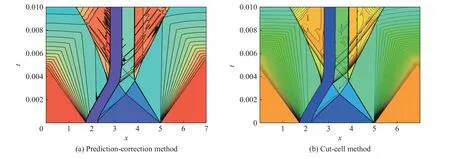
图9 两种方法获得的流场密度 ρ (x,t)云图Fig.9 Mass density ρ (x,t)contours of the fluid by two methods

总体而言，该算例证明了本方法在一维刚体的流固耦合问题中能取得较准确的结果，并证明了该方法是一阶收敛的。

5.2 激波冲击平板

为了检验该方法在弹性结构流固耦合问题中的准确性，开展了相应的实验和数值模拟。考虑一个激波与弹性平板耦合问题。如图10所示，假设存在静止的二维均匀流场，计算域为(−120,60)×(0,65) ，单位为mm，下同。在( 0,4)×(0,50)区域内放置一块有机玻璃板，下方边缘固定。流场介质为多方指数 γ =1.4 的理想气体，初始流场的密度为1.29 kg/ m3，压力为101.3 kPa。有机玻璃板的密度为1 180 kg/ m3，弹性模量为3.1 GPa，泊松比为0.4。在流场右边界输入一个马赫数为1.2的激波。

图10 激波管初始条件（蓝色部分为有机玻璃板，灰色部分为静止流场，右侧红色部分为输入边界）Fig.10 Initial conditions of the shock tube(The PMMA panel is blue,the static fluid is grey,the right boundary in red color is the inflow.)

实验装置的主体为一个激波管，实验段如图11所示。在激波管实验段的下壁面安装一个刚性基座，并在基座靠近前端位置插入平板。实验段内初始气体为空气，激波的驱动气体为氮气。实验期间使用高速相机拍摄光学纹影。

图11 激波管实验段（底部的金属方块为基座，竖立薄片为实验测量的平板）Fig.11 Experimental section of the shock tube(The metal block on the bottom is the base,and the vertical sheet is the tested panel.)

在数值模拟中，对模型进行了简化，略去了基座部分。流场使用均匀正交网格，单元密度为3 mm−1。平板的有限元网格包含253个Q4单元。局部网格如图12所示。

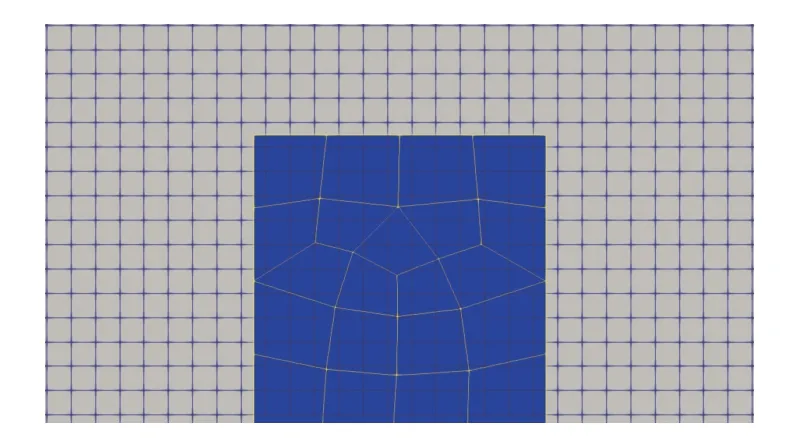
图12 局部网格（灰色部分为流场，蓝色部分为平板）Fig.12 Local grids(The fluid is grey,and the panel is blue.)

图13展示了实验光学纹影与数值模拟纹影的对比。各时刻对比图中上方为实验纹影，下方为模拟纹影，即密度梯度云图。模拟结果表明，激波向左运动一段时间后接触平板，产生反射和绕射。绕流在平板上端右侧顶点形成一个较大的涡。绕射后的激波改变方向，在平板后方的下壁面发生反射。在190～456 µs期间，绕流产生的涡逐渐扩大半径并显示出脱落的趋势。在456 µs时刻下壁面反射波与逐渐扩大的涡接触。通过对比实验纹影，证明了模拟结果基本正确。图14展示了在0～456 µs时间内实验测量的平板的最大挠度与数值模拟结果的对比，证明使用的数值模拟方法能够较准确地预测平板在激波作用下的变形。

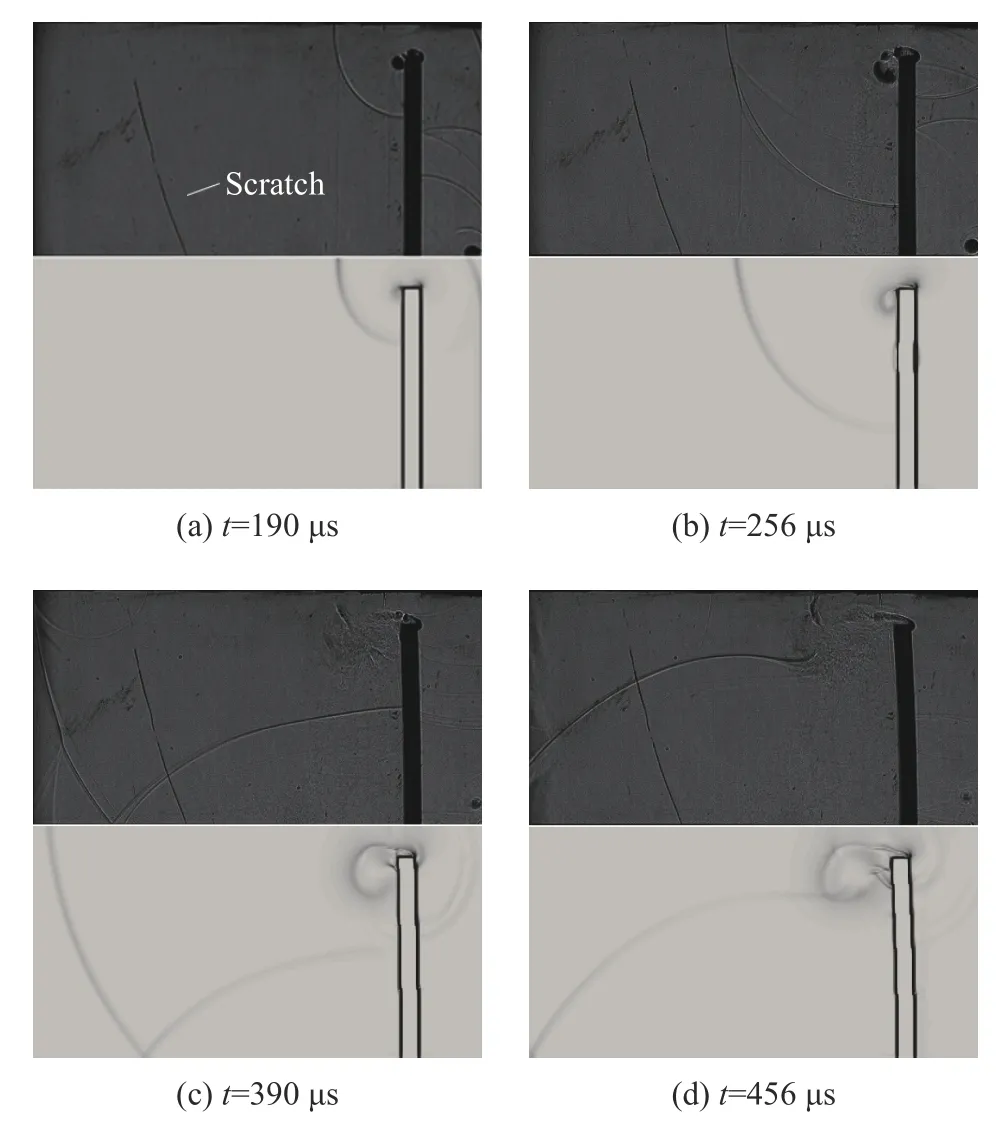
图13 不同时刻实验纹影与模拟纹影的对比Fig.13 Comparison of experimental and simulated

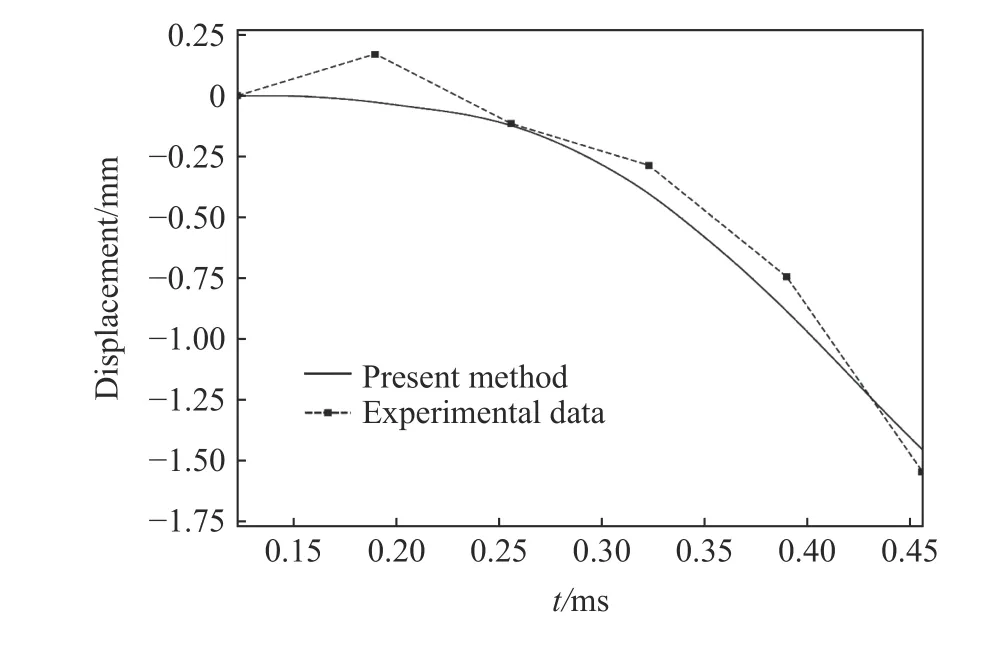
图14 平板的最大挠度Fig.14 Maximum deflections of the panel

值得注意的是，图13中实验拍摄和模拟的激波速度存在小幅度的偏差，推测形成这一偏差的主要原因可能来自于实验的误差。理想条件下，在实验过程中可以通过调节压缩参数改变激波管产生的激波，达到预设的马赫数。但实际操作时会有一些不稳定因素，比如当天的气温较低、导致空气介质密度和压力变化、管道轻微漏气等，这些因素使得真实的马赫数偏离预设的马赫数。此外，由于实验纹影照片分辨率的限制，根据实验纹影照片来确定时间零点也会造成测量误差，因此该实验方案仍有改进的空间。

6 结 论

讨论了锐利浸入边界法中的质量不守恒问题，指出守恒性与网格拓扑相关，提出了一种基于网格拓扑的预估-校正浸入边界法。首先建立了流固耦合系统的演化模型，推导了强耦合的预估-校正格式。接着阐述了求解器和边界处理方法，分析了流固耦合系统各介质的子域及其边界的变化过程，给出了校正算法的具体步骤。对校正算法的推导过程表明，该算法不需要构造虚拟网格，因此避免了虚拟网格法引起的质量误差。同时，该算法不计算截断单元的体积变化，显著简化了算法的实现。

用该方法分别计算了一维刚体和二维线弹性平板的流固耦合问题，并与虚拟网格法和截断单元法的结果进行对比。计算结果表明，该方法在一维刚体和二维线弹性平板的流固耦合问题中均能取得较准确的结果。在一维问题中，该方法严格地维持了全流场质量守恒，与理论预测一致；在二维问题中，该方法准确预测了激波与平板的相互作用过程，与实验测量结果基本吻合。总体而言，该预估-校正浸入边界法相比于传统的虚拟网格法和截断单元法具有精确质量守恒和易于实现的优势，可作为一种替代方法。其主要缺陷在于一阶精度相对较低，有待后续研究完善。