真空干泵用屏蔽电机抗冲击持续带载能力评估与实验

安跃军，陈嘉伟，邓文宇，王光玉，孙宝玉，孔祥玲，齐丽君，李明，4

(1.沈阳工业大学 电气工程学院，沈阳 110870；2.沈阳中北通磁科技股份有限公司技术中心，沈阳 110159； 3.中国科学院沈阳科学仪器股份有限公司，沈阳 110168；4.渤海大学 控制科学与工程学院，辽宁 锦州 121013)

0 引 言

近年来,受半导体制造、液晶注入、光伏器件、薄膜等新兴行业的不断涌现和化工、制药等传统行业的带动,真空应用的领域在不断地扩大，对真空泵的要求也越来越高[1-2]。为满足真空应用发展的需要，真空获得设备的发展正在进入一个新的时代，其特点是：降低泵的振动和噪声，提高长期运行的可靠性，降低能耗和运行成本，获得清洁、无油的真空环境等。传统的真空系统已经不能满足实际工况的要求，具有可靠性高、适应性强、无污染的真空干泵已经成为真空获得设备的一个重要的研究方向[3-4]。

在工业生产中，真空泵往往会与电机设计成一体结构，这样有利于真空系统中真空度的保证。而作为而真空干泵动力核心的屏蔽驱动电动机，其性能直接影响了真空干泵的过载能力、振动噪声、极限真空度以及能耗等级[5-6]。由于真空泵运行时工况比较复杂，电机在稳定运行阶段由于机械原因或系统故障，真空系统中的漏气速率有可能会出现瞬间增大的情况，当冲击载荷处于电机最大转矩范围内时，这种突然增加的负载可能会导致电机持续过载[7]，且随着电流增大，电机温升也会增高，极易使电机过热甚至损坏电机从而造成一定经济损失。因此，在电机的温升限制下准确定量的计算电机抗冲击持续带载能力，可以实现发掘电机的负载潜力满足真空泵电机特殊的工况需求同时，保证电机安全运行，具有十分重要的理论价值和实际工程意义。对于电机负载能力的分析，已有一些学者作出了如下的研究，文献[8]采用经验公式法计算抽油机电动机变负载运行时的等效转矩，通过与电机额定转矩的比较进行热校合，选择合理的负载率保证电机安全运行。文献[9-11]从电机结构、电磁负荷、极限热负荷等方面出发，对短时高过载永磁电机的极限输出能力进行了研究，并计算了电机在高过载下的运行时间。文献[12]提出了一种考虑定子散热以及定转子间传热系数与电机频率变化关系的改进双质量热模型，通过计算电机不同频率下运行时的瞬态加热过程，实现变频调速系统电机合理容量选择，并防止电机过热。文献[13]搭建了电机及逆变器的总成模型，对一台新能源汽车用12 kW高速感应电机的热过载能力进行了研究，并通过双电流模拟实验得到样机极限温升下的工作时间。文献[14]提出了定子绕组热性能直接设计法及其关键热参数，以关键热参数作为热性能设计控制参数, 预测电机各种工况的稳态温升，并根据电机的最高温度，还可以设计预测电机的最大持续工作区域。文献[15]对电机不同负载情况下的热负荷特性进行了分析，并提出了相应实验方法。但是上述文章并没有结合电机的实际运行工况，考虑冷却水温对电机持续带载能力的影响，对于准确定量计算电机持续过载时最热点的完整温升过程曲线研究并不深入。

根据本文研究的真空干泵实际运行条件要求，现场提供的冷却水温主要有25 ℃和33 ℃两种。所以本文结合工程实际，采用有限元分析软件计算电机在两种冷却条件下额定运行时的稳态温度场，确定电机的最热点存在安全裕量。在此基础上，综合考虑电机的最大转矩和绝缘限制，对两种冷却条件下电机的抗冲击持续带载能力进行定量计算，并通过对电机进行测试实验，验证计算结果合理性。

1 电机的三维稳态温度场仿真

1.1 电机参数及温度场数学模型

以一台5 kW真空干泵驱动用屏蔽感应电机为研究对象，该电机的具体结构如图1所示。

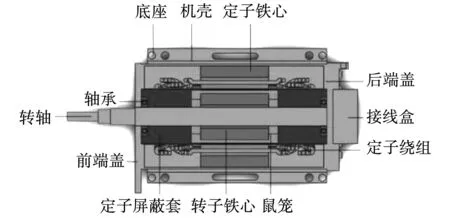
图1 5 kW屏蔽电机的三维模型Fig.1 3D model of 5 kW canned motor

其中电机定子内侧采用屏蔽套进行屏蔽，隔离转子和机壳腔体，保证真空环境绝对无泄漏[16]。屏蔽套采用非导磁材料Sus316L，电机驱动方式为变频器驱动，冷却方式为水冷，表1为电机基本参数。

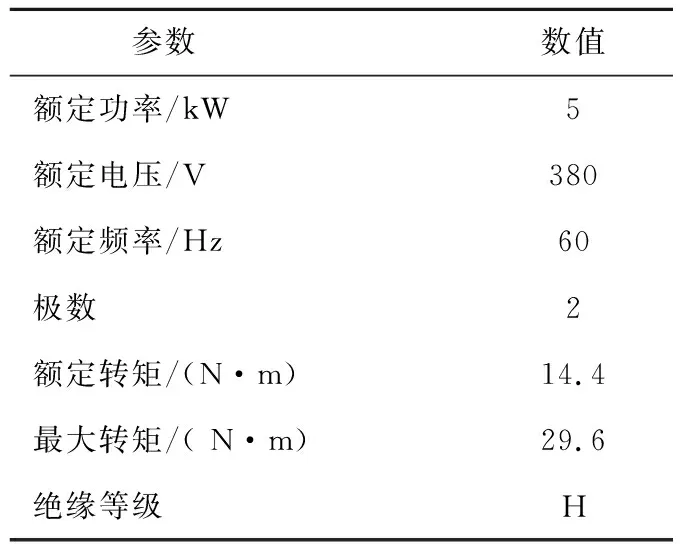
表1 电机的基本参数

根据电机整体结构和电机基本参数，建立的电机温度场求解域三维物理模型如图2所示。

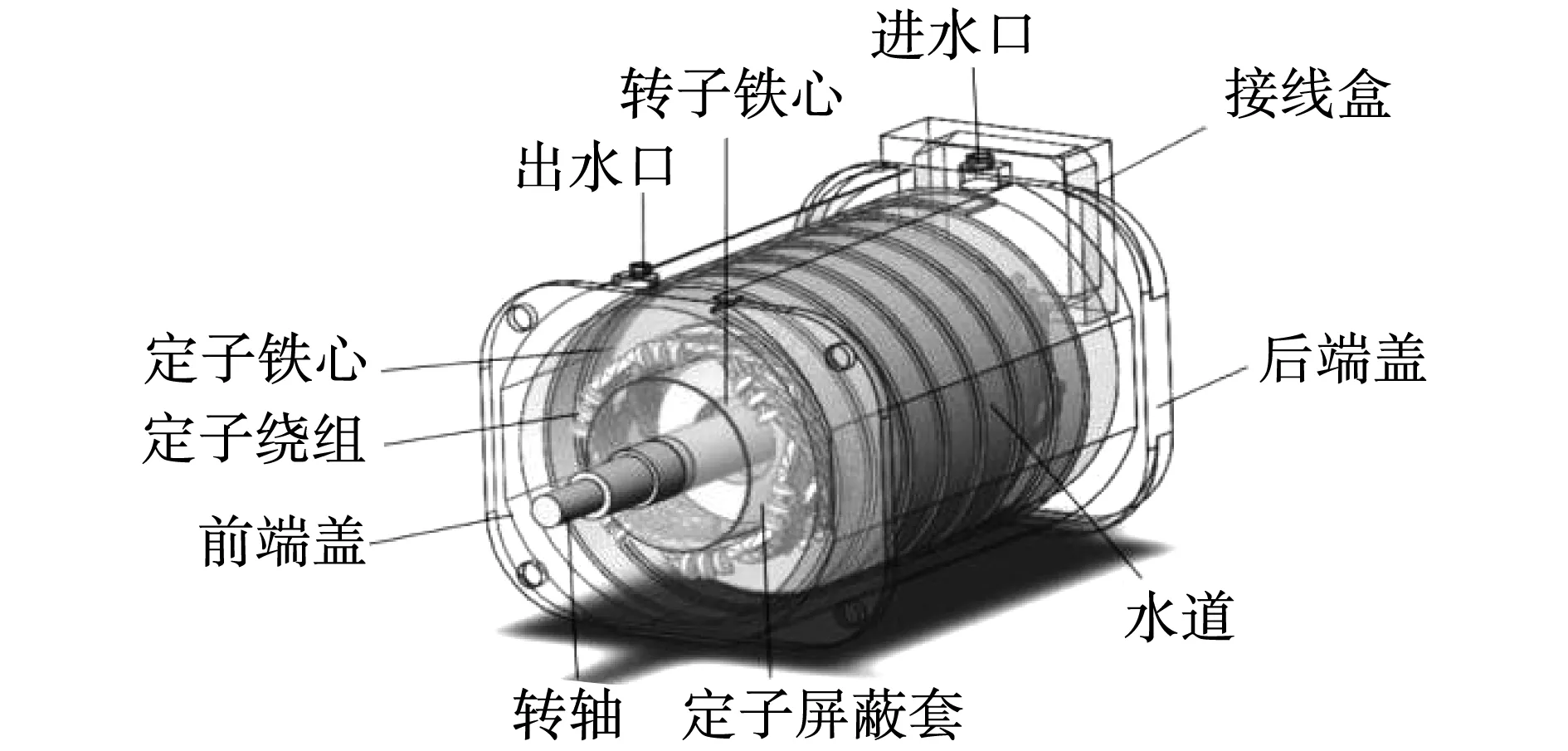
图2 5 kW屏蔽电机的温度场仿真三维物理模型Fig.2 3D physical model of temperature field simulation for 5 kW canned motor

根据传热学理论，对于各向同性介质，真空泵所用驱动电机温度场热传导、热对流问题可以通过三维导热方程式加以描述[17-19]，即：

(1)

式中：Kx、Ky、Kz为电动机各介质x、y、z方向的导热系数；T为温度，℃；q为热源密度，W/m3；n为边界法向量；S1为电动机绝热边界面；S2为电动机散热边界面；Te为S2周围的介质温度，℃；α为S2面的散热系数，W/(m2·℃)；K为S1和S2面法向导热系数，W/(m2·℃)。

针对屏蔽电机内的瞬态温度场研究，根据传热学原理可知，对于瞬态温度场进行求解时，导热方程应考虑时间项，且对于各向同性介质，导热系数为常数。在直角坐标系下的求解域内三维瞬态热传导及其边界条件为[20]：

(2)

式中：T为物体温度，℃；T0为边界上已知的温度分布，℃；Te为周围介质的温度，℃；Kx、Ky、Kz为电动机各介质x、y、z方向的导热系数；S1、S2、S3分别为电机的温度边界、热流边界和对流换热边界，在样机的瞬态场求解中给出了第二类和第三类边界条件，即给电机对应部分赋值对应的热源密度，将机壳作为电机的散热边界；q为热源密度，W/m3；t为时间，s；q0为通过边界面S2的热流密度，W/m3；n为边界法向量；α为散热系数，W/(m2·℃)；K为导热系数；ρ为物质密度，kg/m3；c为物质比热容，J/(kg·℃)。

由于屏蔽电机的结构特殊，定子内侧的屏蔽套使电机转子完全密封，转子处于高度真空的状态，辐射换热成为主要散热方式，所以应该考虑定子屏蔽套内表面和转子外表面的辐射散热。在真空环境中，考虑两面间热辐射的计算问题；根据史蒂芬—波尔兹曼法则和相互作用法则可以得到方程[21-22]

(3)

式中：Qi-j是由平面i到j平面传递的热量，W；Ai是平面i的面积，m2；Fij是两个平面的角系数，与面积、方向和距离有关；ε是平面的总发射率；Ti和Tj分别为两个平面的温度，℃。

定子绕组及绝缘结构复杂，定子槽内导热系数较难计算，所以采用文献[23]的方式进行简化。其导热系数采用下式进行求解计算：

λeq=

(4)

式中：δi(i=1，2，3，…，n)为槽内材料的等效厚度；λi(i=1，2，3，…，n)为槽内材料的导热系数；λeq为槽内材料的等效导热系数。

1.2 热源及边界条件的确定

本文利用有限元分析软件对电机额定工况下的电磁场进行计算，得到电机各部分的损耗分布。其中由于屏蔽套的存在会产生比例较大的涡流损耗，所以计算时应该考虑该部分损耗。同时将电机的损耗与体积的比值即热流密度作为热源，均匀的赋值给电机模型各部分。具体损耗分布如表2所示。

表2 电机的损耗分布

边界条件：考虑高度真空条件下的屏蔽套内表面与转子外表面的辐射作用，两种材料的发射率分别为0.16和0.2[24]。电机机壳表面为散热面，液冷机壳散热系数。根据流体的相似性准则[25-26]，有：

(5)

式中：Nus为流体的努尔特数；αs为机壳表面与流体的热交换系数，W/(m2·K)；Prs为流体的普朗特数；λs为流体的导热系数，W/(m·K)；μ为流体的动力粘度，Pa·s；cp恒压热容，J/(kg·K)；Res为流体雷诺数；ρ为流体密度，kg/m3；νs为流速，m/s；l为特征尺寸，m。在流道截面形状不规则时，采用当量直径de，其表达式为

de=4S/P。

(6)

式中：S为流体过流截面积，m2；P为湿润周长，m。Res和Nus与流体的流动状态有关，本文中流体的流动为紊流，则有

[1+(de/L)2/3](Prs/Prw)0.11。

(7)

式中：Prw为由壁面温度tw确定的流体普朗特数；L为管道长度。可得机壳表面的散热系数为

αs=Nusλs/de。

(8)

样机采用的水道形式为螺旋水道，冷却水进水流量为6.5 L·min-1，水道尺寸为2.5 mm×15 mm，周向水道数为6周，相邻水道间隔为5 mm。计算得到机壳的等效散热系数来等效对流换热，其中25 ℃时的等效对流换热系数为3 077.50 W/(m2·K)，33 ℃时的等效对流换热系数为3 586.87 W/(m2·K)。环境温为室温25 ℃。

1.3 电机额定运行时稳态温度场的分析

根据所建立的模型，将有限元计算得到的各部分损耗分别赋值给定子绕组，转子鼠笼，定子铁心，转子铁心以及屏蔽套等电机的发热部件。并添加相应边界条件，分别得到电机在两种冷却条件下额定运行时稳态温度分布。其中25 ℃冷却水冷却条件下得到的仿真计算结果分别如图3、图4和图5所示。

图3 冷却水25 ℃时电机整体的稳态温度场Fig.3 Steady temperature field of the whole motor at 25 ℃ cooling water

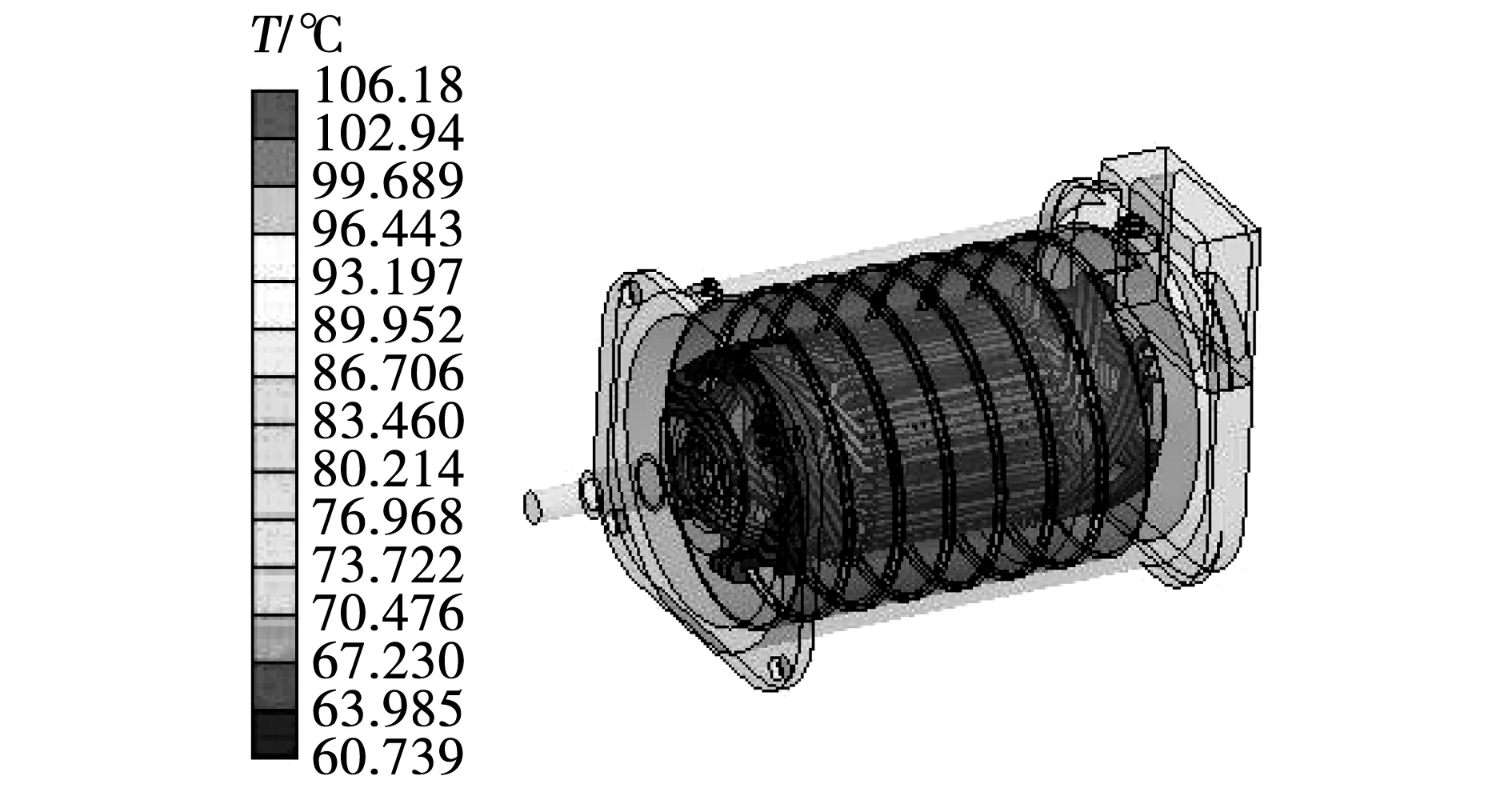
图4 冷却水25 ℃时电机的定子绕组温度分布Fig.4 Temperature distribution of motor stator winding at 25 ℃ cooling water

图5 冷却水25 ℃时电机的转子鼠笼导条温度分布Fig.5 Temperature distribution of rotor bar of motor at 25 ℃ cooling water

由计算结果可知，电机的最热点温度为106.18 ℃，位于定子绕组端部。从轴向上看定子绕组两端温度较高，中间温度较低。这主要是由于定子绕组端部伸出铁心且至于空气中，空气的转热能力较差，而定子绕组铁心内部分与铁心接触充分，热量通过铁心传递。对于转子部分，由于屏蔽套内部处于高度真空状态，散热较差，所以转子鼠笼温度较高，最高温度在端环处，达到81.97 ℃。

水温33 ℃时的计算结果分别如图6、图7和图8所示。

图6 冷却水33 ℃时电机整体的稳态温度场Fig.6 Steady temperature field of the whole motor at 33 ℃ cooling water

图7 冷却水33 ℃时电机的定子绕组温度分布Fig.7 Temperature distribution of motor stator winding at 33 ℃ cooling water

图8 冷却水33 ℃时电机的转子鼠笼导条温度分布Fig.8 Temperature distribution of rotor bar of motor at 33 ℃ cooling water

同样在33 ℃的冷却水温下，由计算结果可知电机最高温度仍位于定子绕组端部，最高温为114.69 ℃。此外，由于转子部分没有直接接触机壳，所以冷却水温改变后转子鼠笼导条温度变化较小。在此种冷却条件下转子鼠笼最高温度为86.07 ℃。

根据真空泵的实际运行条件要求，对25 ℃和33 ℃两种冷却条件下的稳态温度场计算结果进行分析可知，电机的最热点温度还有一定的安全裕量。由于定子绕组端部温度最高，且温升较快会最先达到绝缘限制，在对电机持续带载能力评估时应该重点关注定子绕组端部温升的瞬态变化过程。

2 真空泵电机抗冲击持续带载能力评估

通过电机额定状态下温度场计算的结果可知，最热点温度仍存在安全裕量，电机的负载能力有待于进一步发掘。因此以额定条件下的计算结果作为初始条件，通过设置过载转矩来模拟冲击载荷，每次以1 N·m增加负载转矩，不考虑由电机控制器产生的动态特性因素，并且确保负载转矩小于最大转矩。依次对电机在各过载转矩下的瞬态温度场进行计算，得到最热点在不同负载率冲击载荷下连续过载运行时的温升情况，具体流程如图9所示。

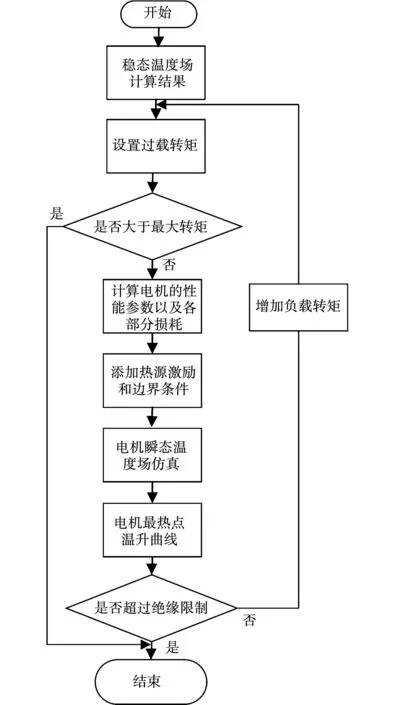
图9 电机持续带载能力评估流程图Fig.9 Flow chart of motor continuous load capacity evaluation

2.1 冷却水25 ℃条件下电机持续带载能力

将稳态温度场计算结果作为初始条件，设置初次过载转矩为15.4 N·m。分析可知过载转矩仍在最大转矩范围内，因此，通过有限元软件计算出电机的各部分损耗情况，依然运用建立的电机三维模型和边界条件进行电机的瞬态温度场分析，并将计算结果作为下一次仿真计算的初始条件。逐次增加负载转矩，并保证转矩小于29.6 N·m，重复之前过程计算电机瞬态温度场，并以每次的仿真结果作为下一次的初始条件，得到在各过载转矩下最热点的瞬时温升曲线和定子绕组温度分布，直到最热点温度达180 ℃的绝缘限制。其中25 ℃时电机最热点的温升情况如表3所示。

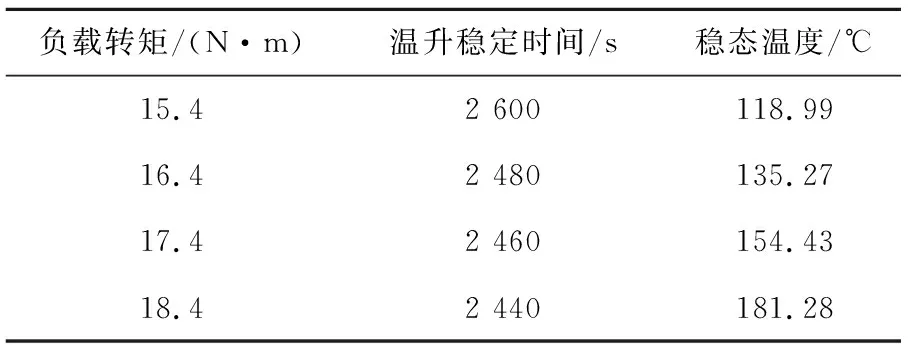
表3 冷却水25 ℃时不同过载转矩下的最热点温度及温升达到稳定所需时间

由表3可知，当电机负载转矩增加到18.4 N·m时，电机负载仍未达到最大转矩，然而此时最热点稳态温度已经突破绝缘限制，继续增加负载会造成电机过热。图10～图13为最热点在各过载转矩下的温升曲线和定子绕组温度分布。

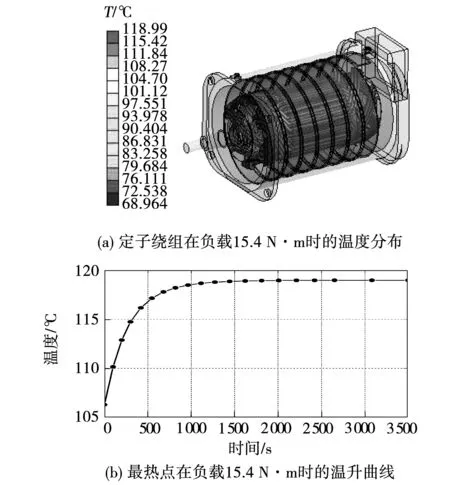
图10 负载15.4 N·m时定子绕组温度分布与 最热点温升Fig.10 Temperature distribution and hottest spot temperature rise of stator winding under 15.4 N·m load

如图13所示，当负载转矩增加至18.4 N·m时，根据电机最热点的温升曲线可知，电机在运行745 s后定子绕组最热点温度达到180 ℃的绝缘限制，继续运行电机将存在安全隐患。为更全面的分析电机负载能力，改变冷却条件，对另一常用的33 ℃冷却水温情况下电机在冲击载荷下持续带负载能力进行仿真计算。

图11 负载16.4 N·m时定子绕组温度分布与 最热点温升Fig.11 Temperature distribution and hottest spot temperature rise of stator winding under 16.4 N·m load

图12 负载17.4 N·m时定子绕组温度分布与 最热点温升Fig.12 Temperature distribution and hottest spot temperature rise of stator winding under 17.4 N·m load

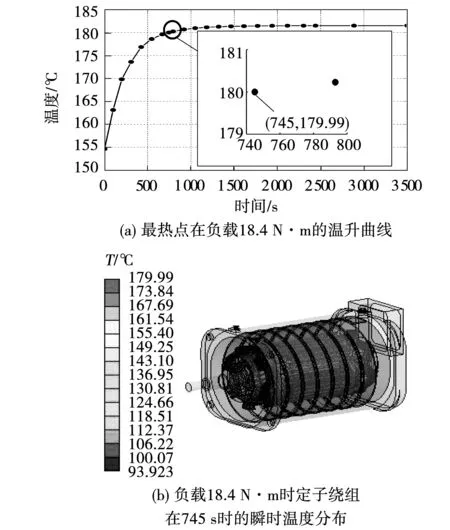
图13 负载转矩18.4 N·m时最热点温升与定子绕组达到绝缘限制时的温度分布Fig.13 Temperature rise of the hottest spot and temperature distribution of the stator winding when the load torque is 18.4 N·m

2.2 冷却水33 ℃条件下电机持续带载能力

仿真过程与25 ℃冷却水时仿真过程相同，在电机的最大转矩范围内，设置过载转矩模拟冲击载荷，通过对电机在各过载倍数下的瞬态温度场的进行仿真计算，得到电机运行在不同负载率的冲击载荷下连续过载运行时最热点的温升情况进行计算，直到达到绝缘限制。表4和图14分别为电机运行在不同负载率的冲击载荷下连续过载运行时，最热点温升达到稳态时所用时间和稳态温度以及最热点的温升曲线。

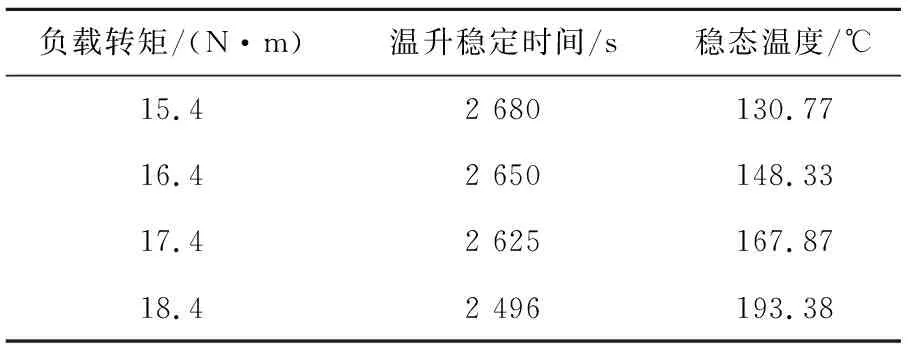
表4 冷却水33 ℃时最热点在不同过载转矩下温升达到稳定所需时间及稳态温度

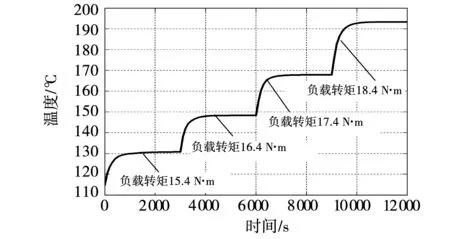
图14 冷却水温33 ℃时最热点在不同过载倍数下 温升曲线Fig.14 Temperature rise curve of the hottest spot of stator winding under different overload times when water temperature is 33 ℃

由图14和表4可知，在33 ℃冷却水温下，电机在17.4 N·m及以下仍可以长时间安全运行。当负载增加到18.4 N·m时，电机在更短时间内突破绝缘限制。其中电机转矩18.4 N·m情况下的最热点温升和达到绝缘限制时定子绕组温度分布如图15所示。

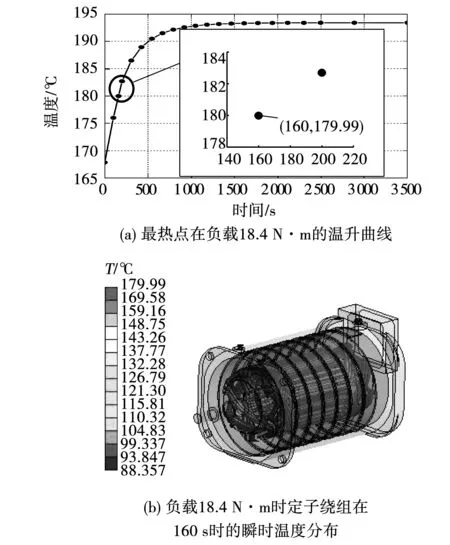
图15 负载转矩18.4 N·m时最热点温升与定子绕组达到绝缘限制时的温度分布Fig.15 Temperature rise of the hottest spot and temperature distribution of the stator winding when the load torque is 18.4 N·m

如图15可以看出，当负载转矩为18.4 N·m时，电机的可安全运行时间减少到160 s。并且通过定子绕组的温度分布可以看出当电机最热点达到绝缘限制时，由于水冷存在，定子绕组铁心内部分温升较慢，温度低于同等情况下水温为25 ℃时的温度。

3 样机测试实验

为验证有限元计算结果以及得到的温升曲线的准确性、合理性。在25 ℃和33 ℃两种冷却水温下对样机进行测试实验。在样机测试前通过在绕组端部绝缘外的不同位置埋置多个pt100传感器，以便测得定子绕组最热点温度位置。实验过程中，保证测试时外界条件和仿真的边界条件相同，即进水口冷却水流量6.5 L·min-1，且首先在25 ℃冷却水温下，测量电机额定运行时的稳态温度，待温度稳定后将负载转矩增加1 N·m。为得到最热点温升曲线，每隔10分钟记录一次示数直到温度稳定。继续增加负载，重复上述步骤直到pt100示数达到180 ℃立刻停机。待电机温度冷却至室温将冷却水温调整到33 ℃重复上述过程。图16为实验测试平台。

图16 电机过载能力测试平台Fig.16 Load capacity test platform of motor

图17和图18分别为两种冷却条件下的仿真计算结果和实验测量结果对比图。

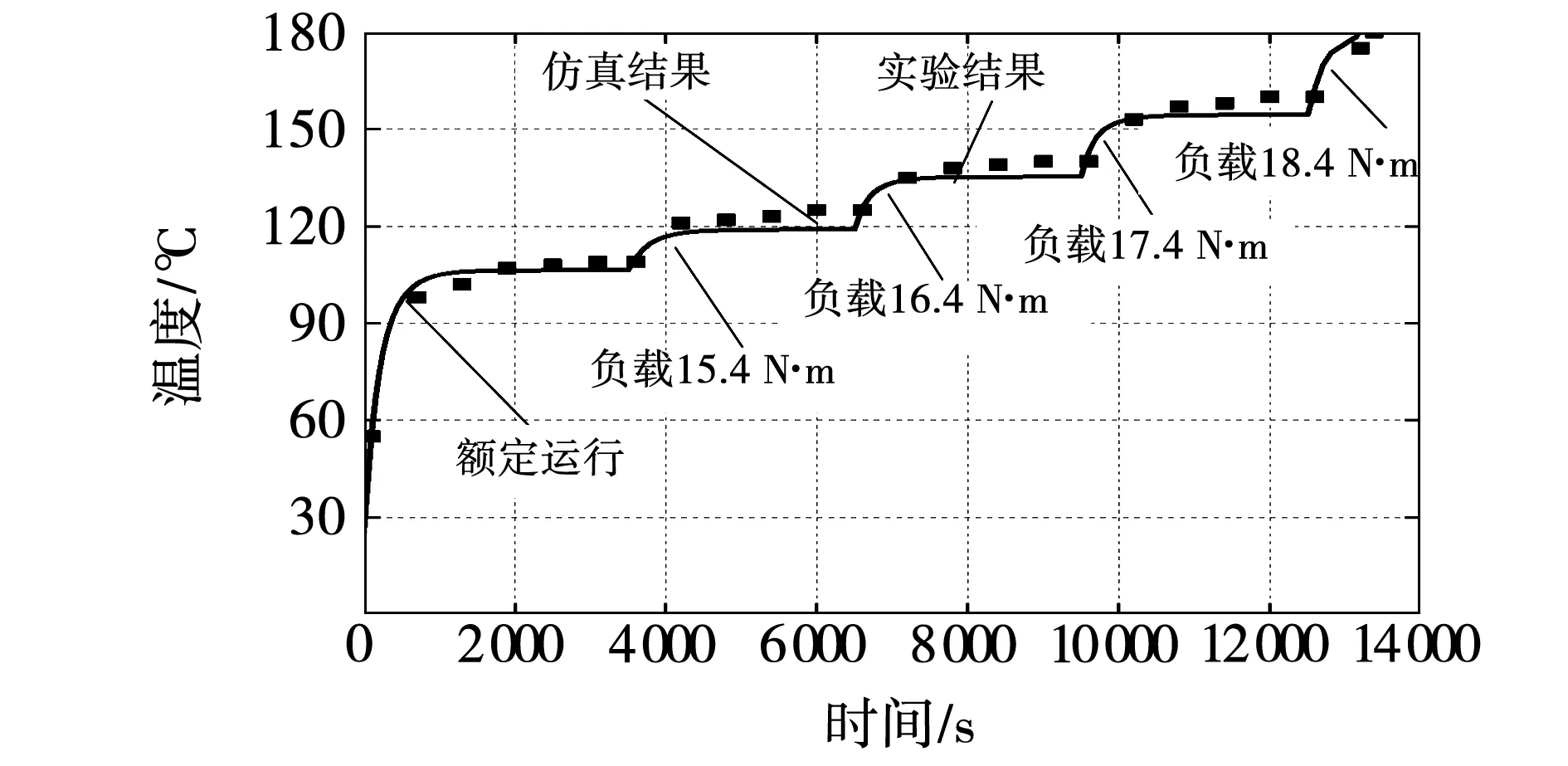
图17 水温25 ℃时最热点温升曲线的实验与仿真结果Fig.17 Experimental and simulation results of the temperature rise curve of the hottest spot at 25 ℃

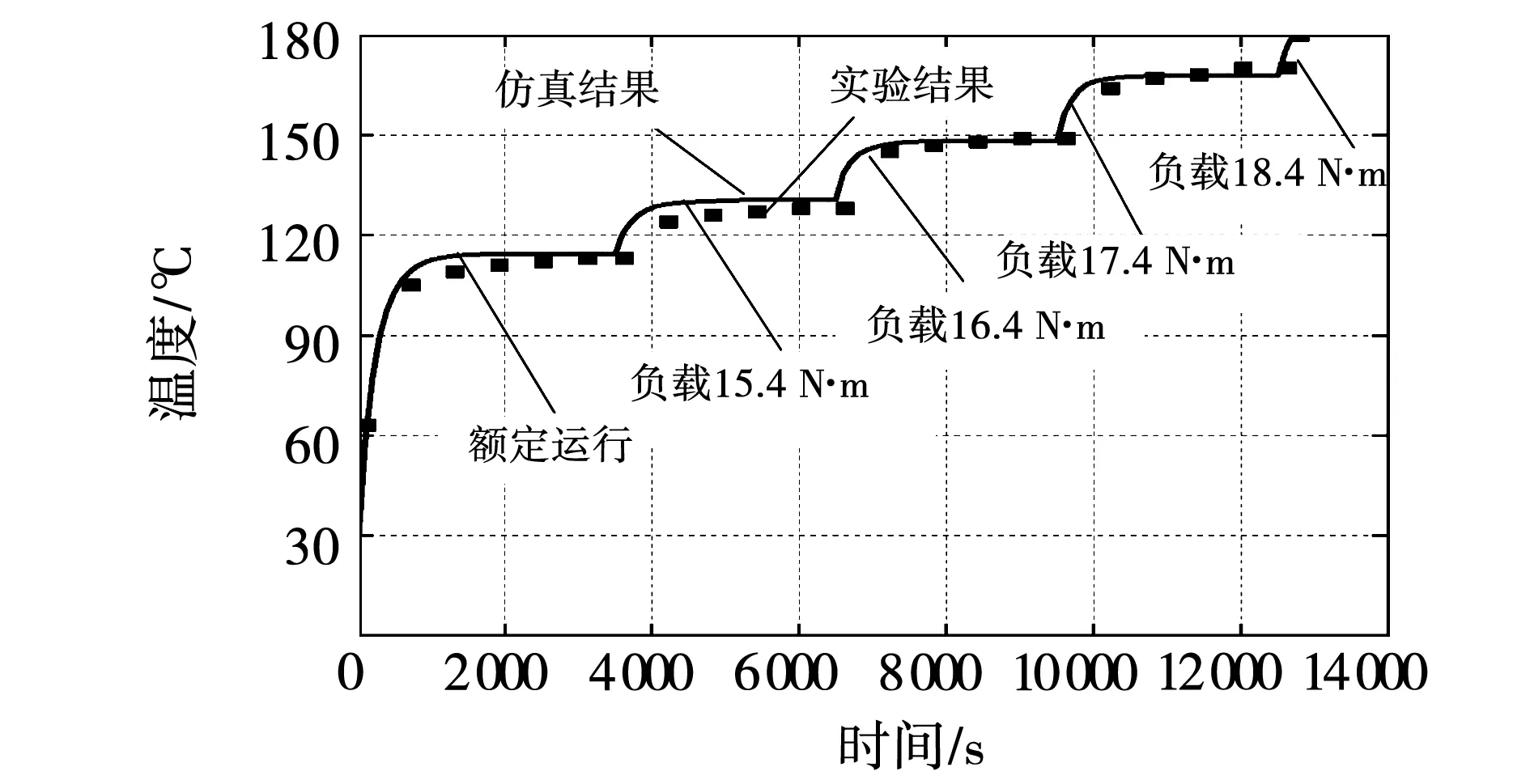
图18 水温33 ℃时最热点温升曲线的实验与仿真结果Fig.18 Experimental and simulation results of the temperature rise curve of the hottest spot at 33 ℃

在两种冷却条件下，由于在仿真计算过程中未考虑到电机的电磁参数、材料属性以及机壳等效散热系数等受温度变化的影响，所以实验和仿真结果之间存在一定的误差，最大误差分别为4.8 ℃和4.2 ℃。在18.4 N·m过载情况下，电机的可安全运行时间的实验测量结果分别为780 s和240 s，与仿真分析得到的结果基本吻合。图19对两种冷却条件下电机的持续带载能力进行了比较。

图19 两种冷却条件下电机的持续带载能力比较Fig.19 Comparison of continuous load capacity of motor under two cooling conditions

由图19可知仅改变冷却水温的情况下，电机最热点的温升曲线趋势基本一致。根据牛顿散热定律可知，在同一负载率下损耗相同时，虽然33 ℃冷却水的等效对流散热系数要略高于25 ℃冷却水，但由于水套内水的平均温度较高，所以散热面温度更高，最热点温度也应高于25 ℃冷却水时，与图22所示结果基本吻合。所以可知在冷却水温为25 ℃时，在同等负载率下过载时电机温度更低，在转矩18.4 N·m时电机的安全运行时间提高了333.33%，电机在特殊工况下具有更高的持续带载能力。

4 结 论

根据真空泵实际工作时的运行条件要求，本文采用有限元计算法对一台5 kW真空干泵用屏蔽电机在两种冷却条件下额定运行时的稳态温度场和突加载荷后持续过载运行时的瞬态温度场进行计算和分析，得到最热点的温升曲线。从电机的最大转矩和绝缘等级两方面综合考虑来对电机抗冲击持续带负载能力进行评估，并对电机两种冷却条件下负载能力进行了对比分析，得到结论如下：

1)两种冷却条件下，电机在额定状态运行时由于定子绕组端部没有与定子铁心直接接触散热条件较差，且定子铜耗较大，所以定子绕组端部为电机的最热点。但距离电机的绝缘限制有一定安全裕量，电机负荷能力有待于进一步发掘。

2)定子绕组端部温度最高且温升较快，最容易突破绝缘限制，通过对过载状态下瞬态温度场计算得到的定子绕组端部最热点温升曲线可知，当电机突加载荷后，在常用的两种冷却条件下，若电机需要长时间连续工作时，过载倍数应控制在1.2以内，当过载倍数处于1.2至1.28之间时在25 ℃和33 ℃两种冷却水温下电机仍可以分别在745 s和160 s以内安全运行。此外，通过与最大转矩的比较可知，电机在上述负载率状态下运行时不会发生堵转。

3)通过电机负载能力测试实验得到的温升曲线验证了最热点温升曲线的仿真结果的准确性和合理性。通过理论上和计算结果两方面对两种冷却条件下电机的持续带载能力进行对比分析可知，电机在25 ℃冷却水温下具有更强抗冲击持续带负载能力。该研究对电机的负载潜力进行发掘了和定量计算，从电机安全运行角度出发，为今后真空泵在特殊工况下运行时，真空泵电机在冲击载荷下连续运行时可承受的安全过载倍数的判断，以及极端条件下电机过热保护装置预留窗口期的更精准确定提供了科学依据。