一种LC单元的双向电压均衡电路

徐顺刚，李康乐，周国华，张小兵，高凯

(西南交通大学 电气工程学院，成都 610031)

0 引 言

近些年来，随着环境污染以及能源危机问题变得日益严重，各国都在积极开发新能源技术。其中锂离子电池、超级电容器这两种分别具有高能量密度和高功率密度的储能单元，已经广泛的应用于各大新能源领域，比如混合动力电动汽车，新能源光伏发电和风能发电等各大领域。正常工作时，锂离子电池和超级电容器的单体电压通常都比较低，锂离子电池正常工作电压是3.7 V左右，而超级电容器正常工作电压是2.7 V左右。因此在大功率场合应用时，通常需要将成百上千个储能单元串联起来满足实际的大功率需求[1-2]。

但是，在锂离子电池和超级电容器实际生产过程中，由于生产工艺等因素的影响，这些储能单体的各项参数不会完全一致，比如不同的容量、内阻、自放电率。这些自身参数的差异，将会导致串联储能单体在工作过程中，各个储能单体电压不一致，从而降低储能单元的能量利用率。比如在放电过程中，当其中一个单体电压已经达到放电下限时，其他串联储能单体能量还没有释放完；或者在充电过程中，当其中一个单体电压已经达到充电上限时，其他串联储能单体能量还没有充满。如果重复的进行这种电压不一致的充放电，不仅会降低能量利用率，缩短使用寿命，更严重的还会造成爆炸等安全问题[3-6]。因此，在这种大数量串联储能单元系统中，研究电压均衡技术，对提高储能单元的能量利用率，使用寿命和安全性具有重大意义。

现有的电压均衡电路从能量角度来看，可以分为能耗型均衡电路和非能耗型均衡电路。其中能耗型均衡电路主要是通过并联在电池两端的耗能元件，比如电阻、晶体管，释放掉多余的能量，从而实现储能单体电压一致[7]。这种能耗型电路虽然电路结构简单，易于控制，但是存在效率低，发热严重的缺点。非能耗型电路则是通过储能元件，比如电感、电容、变压器，实现能量从电压高的储能单体向电压低的储能单体进行转移，最终实现串联储能单元中各单体电压一致[8]。相比于能耗型均衡电路，非能耗型电路虽然需要一些储能元件以及开关管实现能量转移，但是具有较高的均衡效率和速度，因此非能耗型均衡电路是现在主要研究热点。

能耗型均衡电路按照电路结构和能量转移方式，可分为4种类型，分别是整组-单体型[9-11]、单体-整组型[12-14]、相邻单体-单体型[15-17]、直接单体-单体型[18-20]。其中整组-单体型均衡电路是将能量从串联储能单元组向电压最低的单体转移。当串联储能单元组中存在某个单体电压比较低，其他单体电压基本一致的情况时，这种类型的均衡电路具有较大的优势。而单体-整组型均衡电路则是将能量从电压最高的单体向串联储能单元组转移。当串联储能单元组中存在某个单体电压比较高，其他单体电压基本一致的情况时，这种电路具有较大的优势。虽然以上两种类型的均衡电路均可以有效的实现串联储能单元单体电压的均衡。但是这两种电路结构存在能量的循环流动，并且开关管具有较高的电压应力。相比于前两种类型的均衡电路，相邻单体-单体型和直接单体-单体型均衡电路则是通过能量在单体间的转移，实现电压的均衡，具有较高的均衡效率。

在相邻单体-单体型均衡电路中，使用最多的均衡单元就是双向Buck-Boost电路[15-16]和开关电容电路[17]。在基于双向Buck-Boost的相邻单体-单体型均衡电路中，由于能量只通过Buck-Boost电路在两个单体之间转移，因此当需要均衡的目标单体分别位于储能单元组首末两端时，则需要较长的均衡路径进行能量转移。在基于开关电容的相邻单体-单体型均衡电路[17]中，通过一组互补的信号控制开关管工作，控制电路比较简单，进而实现能量通过电容在相邻单体间的转移。由于每个周期中的均衡电流是由相邻两个单体的电压差决定的，随着均衡过程的进行，电压差越来越小，均衡电流也越来越小，导致均衡速度越来越慢。为了解决能量在相邻单体间逐级传递问题，实现任意两个单体之间的能量转移，文献[19]提出了一种基于多绕组变压器的直接单体-单体均衡电路，该电路通过每个单体上的绕组间耦合实现能量在任意单体间的相互转移，但是该电路中的多绕组变压器不仅存在较大的体积，还具有较高的成本。

本文提出一种基于LC单元的双向单体-单体电压均衡电路，该电路采用双向开关单元与LC单元结合的方式，实现能量在串联储能单元组中任意单体之间的转移。该电路不仅有效的减少了储能元件数量，缩短了能量传输路径，不存在能量重复流动，而且具有体积小和扩展性高的优点，可用于任意数量单体的串联储能单元组，每增加一个储能单体只需增加两个开关管。

1 均衡电路介绍

本文所提出的基于LC单元的双向单体-单体电压均衡电路如图1所示，均衡电路包括串联储能单元组(电池/超级电容)、双向开关单元、LC单元三部分。双向开关单元选通均衡目标单体，提供充放电回路，LC单元作为能量转移介质，实现能量在最大电压单体与最小电压单体间转移。

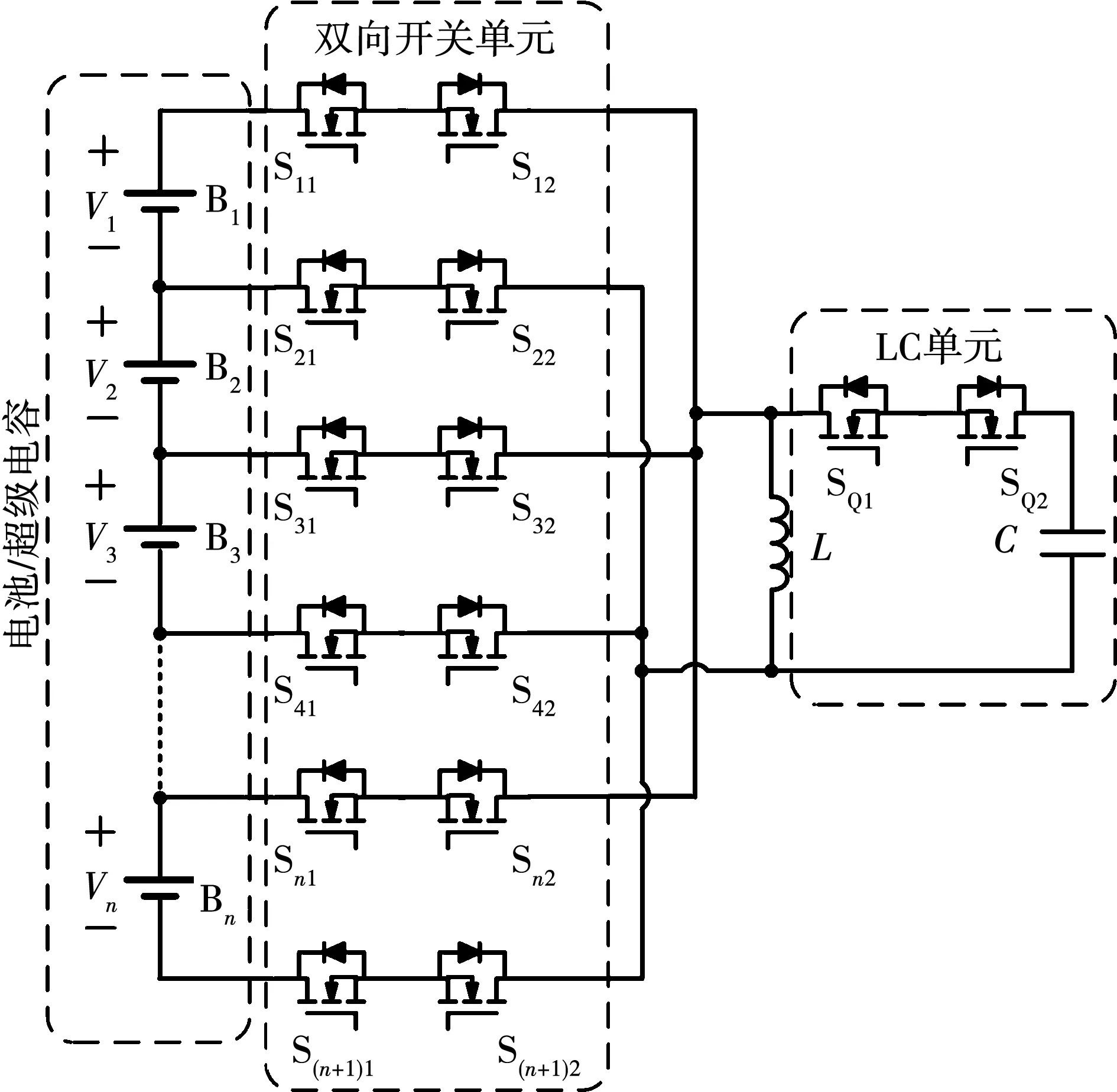
图1 基于LC单元的双向单体-单体均衡电路Fig.1 Bidirectional cell-cell equalization circuit based on LC unit

当n个储能单体串联时，每个单体通过两对双向开关管分别连接至电感L的两端，除去首末两端的储能单体，其它任意相邻两个单体之间均共用一组双向开关(Si1，Si2)。同时电感L又通过一组双向开关(SQ1，SQ2)连接至谐振电容C。假设串联储能单元组中最大电压单体Bi的电压为Vmax，最小电压单体Bj的电压为Vmin，该均衡电路根据串联储能单元组中单体电压位置分布可分为两种工作状态:

工作状态一：当Bi处于奇数位置，Bj处于偶数位置(i=2k-1，j=2m)时；或Bi处于偶数位置，Bj处于奇数位置(i=2k，j=2m-1)时，其中1≤k≤n，1≤m≤n，能量先从Bi转移至电感L，然后再从L转移至Bj。

工作状态二：当Bi处于奇数位置，Bj处于奇数位置(i=2k-1，j=2m-1)时；或Bi处于偶数位置，Bj处于偶数位置(i=2k，j=2n)时，其中1≤k≤n，1≤m≤n，k≠m。能量先从Bi转移至电感L，然后电感L与电容C发生并联谐振，半个谐振周期后，电感电流反向，然后能量再从电感L转移至Bj。

当均衡电路工作时，根据串联储能单元中最大电压单体和最小电压单体位置的分布，可以将这两种工作状态表示为：

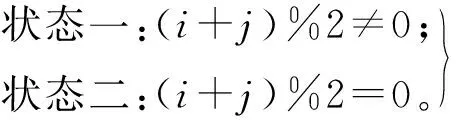
(1)

其中：i和j分别表示最大电压单体和最小电压单体的位置数；%表示求余运算符号。

当该电路工作在状态一时，假设单体B2的电压最大为Vmax，单体B3的电压最小为Vmin，则工作过程中的能量转移路径分别如图2所示，图3为工作状态一的波形。

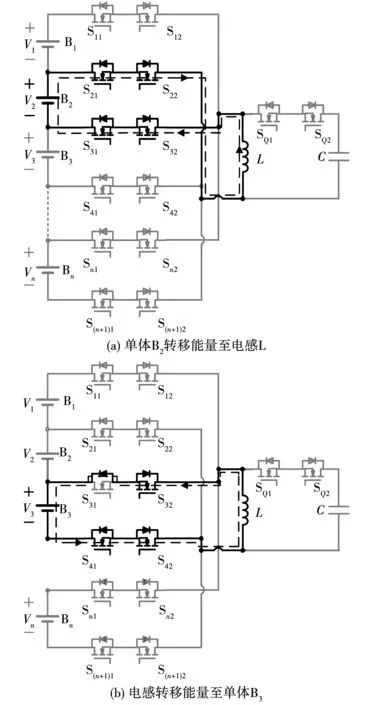
图2 单体B2、B3能量转移路径Fig.2 Energy transfer path of cell B2 and B3

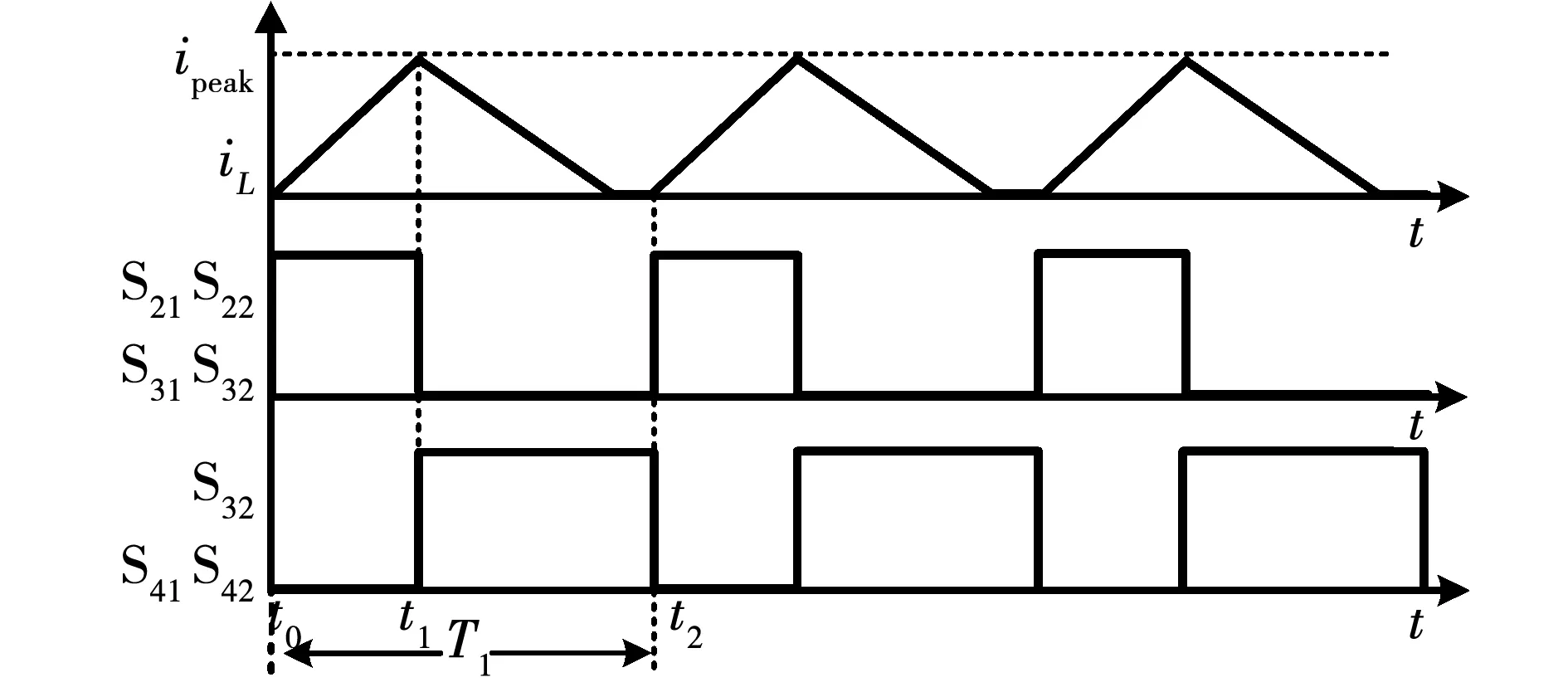
图3 工作状态一的波形Fig.3 Working waveform of state 1

模态1[t0-t1]：如图3所示，在t0时刻，开关管S21、S22、S31、S32导通，电感电流在电压V2的作用下线性上升，直到t1时刻，电感电流上升至最大值。

模态2[t1-t2]：如图3所示，在t1时刻，电感电流上升至最大值，此时开关管S32、S41、S42导通，同时开关管S31的体二极管导通为电流提供回路，防止单体B3对电感反向充电，电感电流在电压V3的作用下线性下降直至为0，即完成一个周期的能量转移。

当该电路工作在状态二时，假设单体B1的电压最大为Vmax，单体B3的电压最小为Vmin，则工作过程中的能量转移路径分别如图4所示，图5为工作状态二的波形。

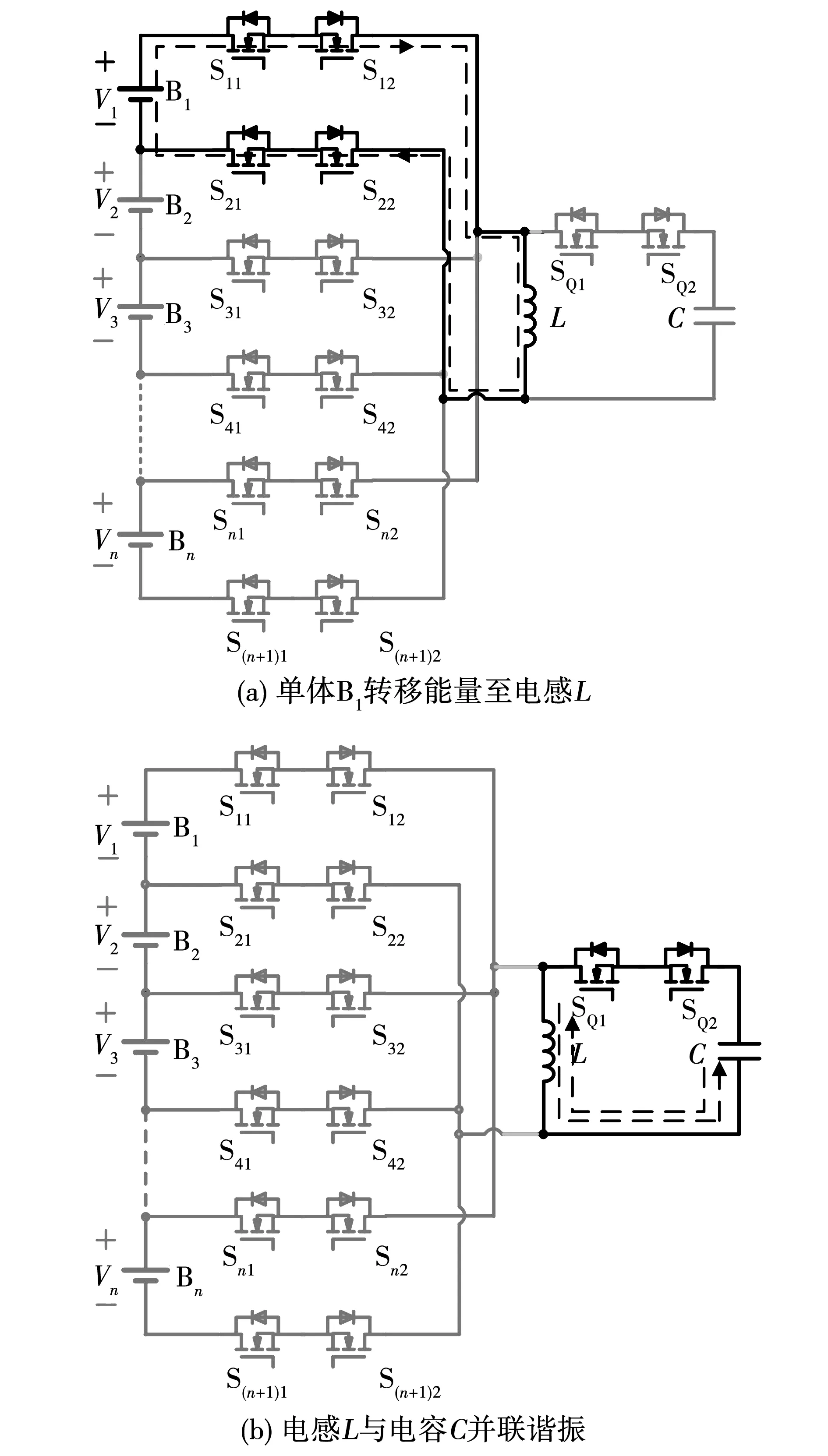
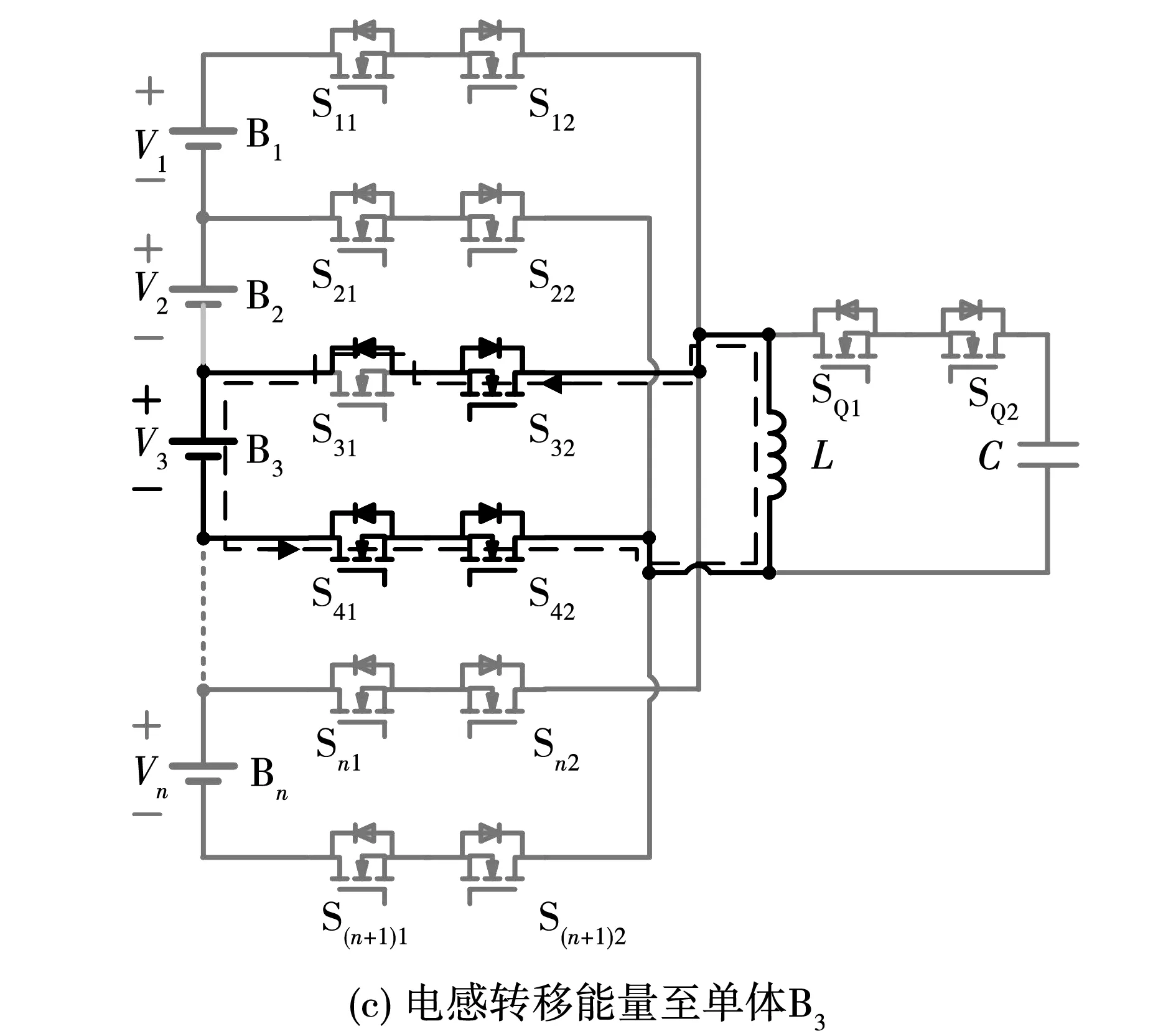
图4 单体B1、B3能量转移路径Fig.4 Energy transfer path of cell B1 and B3

模态1[t0-t1]：如图5所示，在t0时刻，开关管S11、S12、S21、S22导通，电感电流在电压VB1的作用下线性上升，直到t1时刻，电感电流上升至最大值。

模态2[t1-t2]：如图5所示，在t1时刻，开关管SQ1、SQ2同时导通，此时电感L与电容C谐振，时间为半个谐振周期，直至t2时刻，电感电流从正向最大值变为反向最大值。

模态3[t2-t3]: 如图5所示，在t2时刻，开关管S32、S41、S42导通，同时开关管S31的体二极管导通为电流提供回路，防止电池B3对电感反向充电，电感电流在电压VB3的作用下线性下降直至为0，即完成一个周期的能量转移。

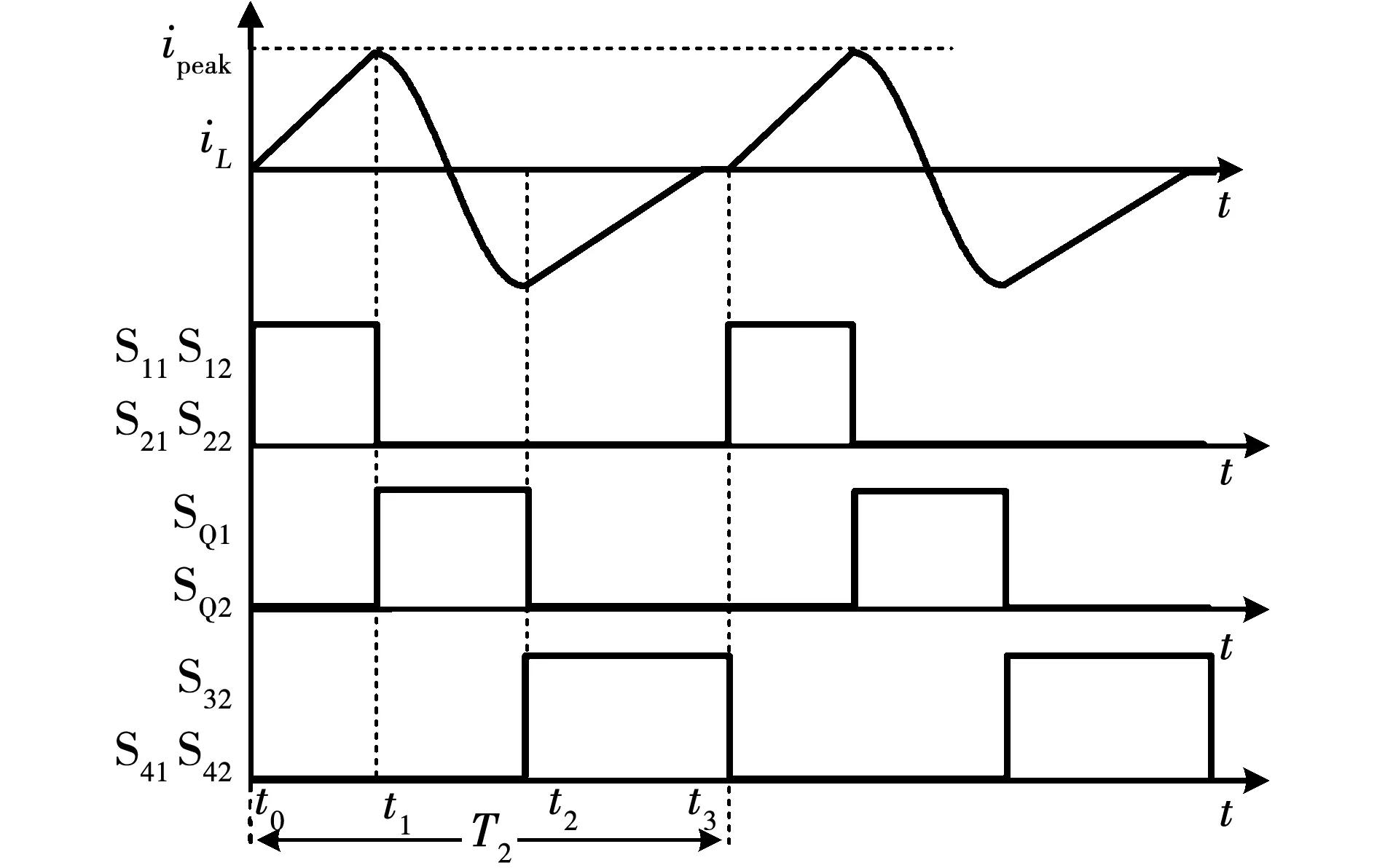
图5 工作状态二的波形Fig.5 Working waveform of state 2

2 电路工作原理分析

为了进一步对该电路进行分析，对该电路两种工作状态下各模态的工作情况进行了原理说明。为了简化分析，做如下假设：1)电路中所有元件均为理想器件，开关管仅有体二极管存在；2)一个开关周期内储能单体两端电压恒定不变。

2.1 工作状态一

当B2和B3的电压分别为串联储能单元组中电压最大的单体和电压最小的单体时，其电压分别为V2和V3，能量将实现从B2到B3的转移。电路处于工作状态一，各模态等效电路如图6所示。

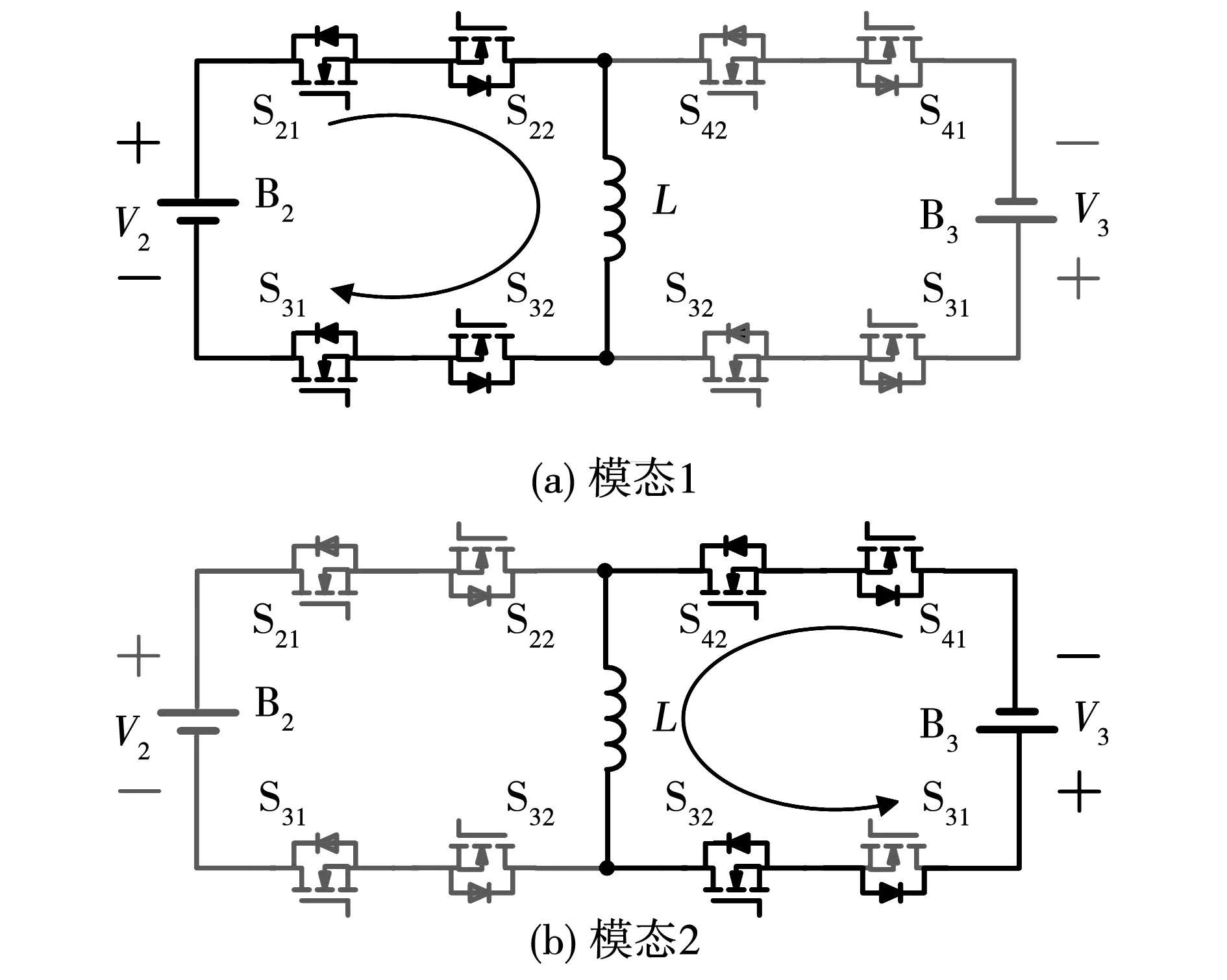
图6 工作状态一各模态等效电路Fig.6 Equivalent circuit of each mode in state 1

模态1[t0-t1]: 如图6(a)所示，在t0时刻，开关管S21、S22、S31、S32同时导通，单体B2向电感L传递能量。如图4所示，电感电流iL在电压V2的作用下从0开始线性上升，电感电流表达式为

(2)

其中t0≤t≤t1，假设该模态持续时间为DT1，D是该模态中开关管的占空比，T1是该工作方式下的工作周期。在t1时刻，电感电流达到峰值，其峰值电流表达式为

(3)

模态2[t1-t2]：如图6(b)所示，在t1时刻，开关管S21、S22、S31、S32关闭，开关管S32、S41、S42导通，同时开关管S31的体二极管为电感电流提供回路。如图3所示，电感电流iL在电压V3的作用下线性下降直至降为0，之后由于开关管S31的体二极管反向截止作用，电路中不再有电流流动。在模态2中，电感电流表达式为

(4)

其中t1≤t≤t2，该模态持续时间为

(5)

其中：D1是该模态中开关管的占空比；T1是工作状态一的工作周期。

2.2 工作状态二

当B1和B3的电压分别为串联储能单元组中电压最大的单体和电压最小的单体时，其电压分别为V1和V3，能量将实现从B1到B3的转移，电路处于工作状态二，各模态等效电路如图7所示。

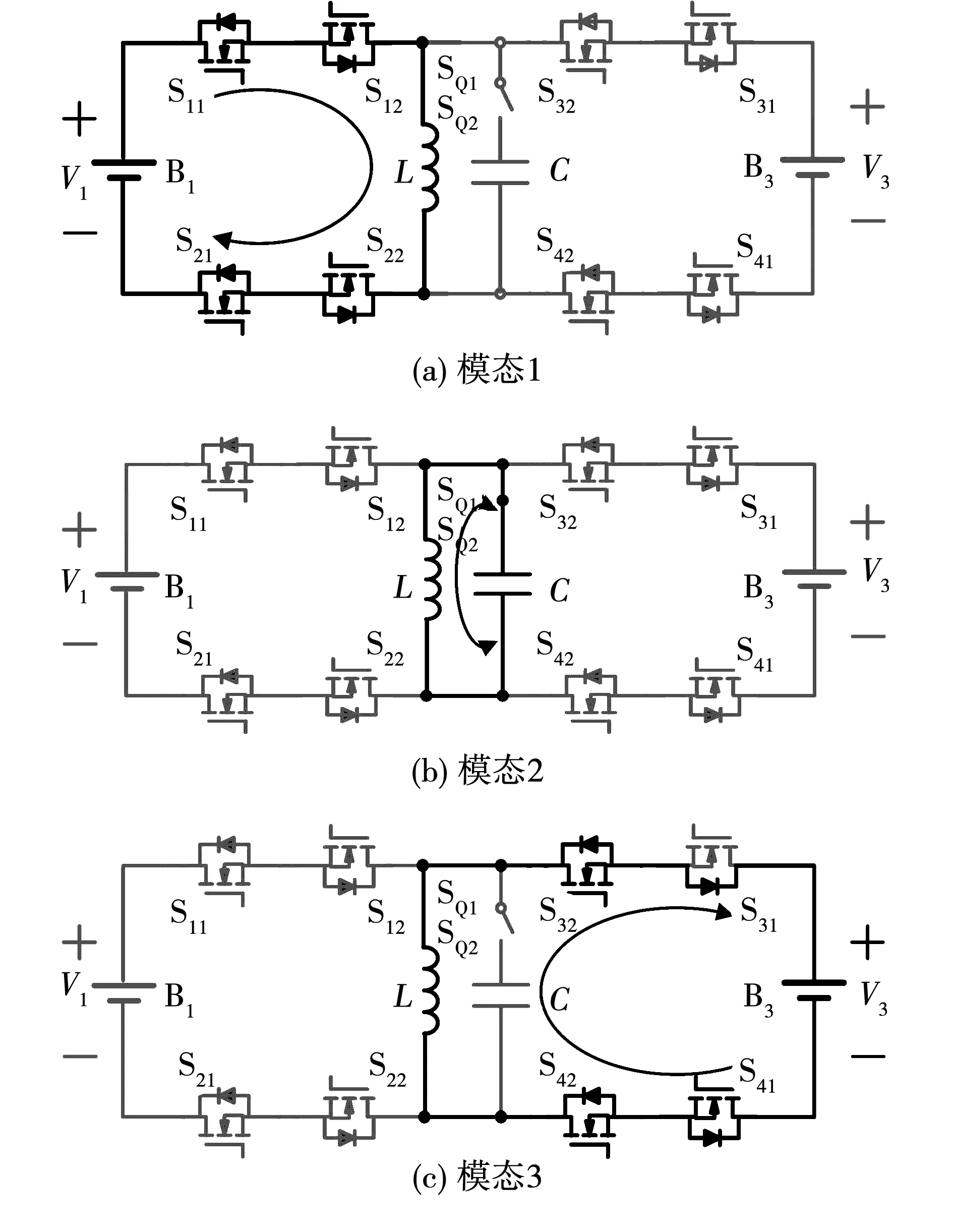
图7 工作状态二各模态等效电路Fig.7 Equivalent circuit of each mode in state 2

模态1[t0-t1]：如图7(a)所示，在t0时刻，开关管S11、S12、S21、S22同时导通，单体B1向电感L转移能量。如图6所示，电感电流iL在电压V1的作用下从0开始线性上升，电感电流表达式为

(6)

其中t0≤t≤t1，假设该模态持续时间为αT2，α是该模态中开关管的占空比，T2是工作状态二的工作周期。在t1时刻，电感电流达到峰值，其峰值电流表达式为

(7)

模态2[t1-t2]：如图7(b)所示，在t1时刻，开关管SQ1、SQ2导通，电感L与电容C发生并联谐振。如图5所示，在t2时刻，谐振电感电流由正向最大值变为反向最大值，然后开关管SQ1、SQ2关断，此时电感电流大小为

(8)

该模态持续时间为

(9)

模态3[t2-t3]: 如图7(c)所示，在t2时刻，当电感电流为反向最大值时，开关管S32、S41、S42同时导通，同时开关管S31的体二极管为电感电流提供回路。如图5所示，电感电流在电压V3的作用下线性下降直至降为0，之后由于开关管S31的体二极管反向截止作用，电路中不再有电流流动。在模态3中，电感电流表达式为

(10)

其中t2≤t≤t3，该模态持续时间为

(11)

其中：α1是该模态中开关管的占空比；T2是工作状态二的工作周期。

在上述两种电路工作状态中，随着均衡过程的进行，最大电压单体和最小电压单体位置的变化，两种电路工作状态交替进行。为了保证均衡电路的功率一致，因此控制两种工作状态中模态一的持续时间保持一致，并且周期T1和周期T2满足以下关系：

(12)

为了保证电路工作过程中，电感电流处于断续模式(DCM)，根据式(3)、式(5)、式(7)、式(11)可得，占空比D和α满足下式关系：

(13)

3 开关工作模式及控制策略

在本文提出的基于LC单元的双向单体-单体均衡电路中，由于在每个开关工作周期开始，首先要对串联储能单元所有单体电压进行精准的采集，然后控制开关单元对目标均压单体进行充放电控制。因此根据所有可能出现的情况，表1给出了该均衡电路在工作时每个周期中开关单元的开关模式状态。

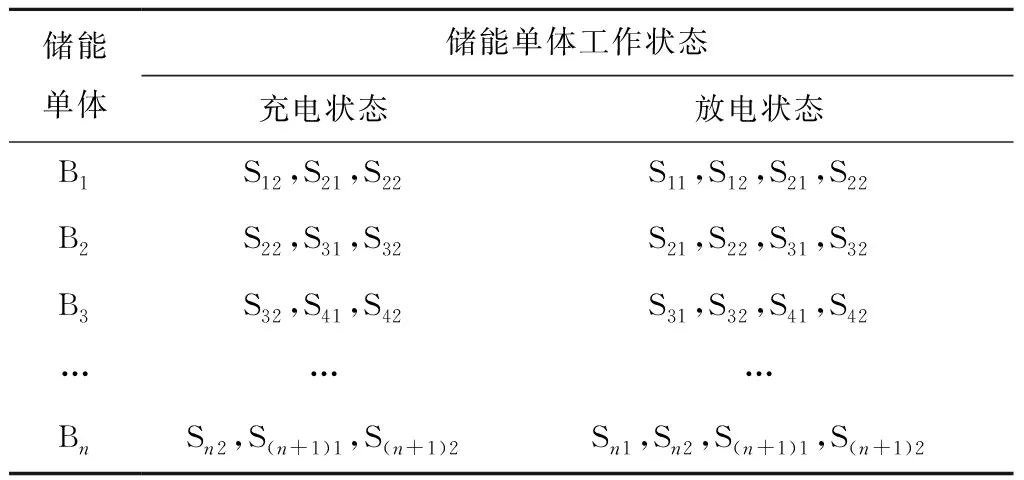
表1 电路工作时的开关单元工作模式

由于该均衡电路在每个工作周期中，都需要精准采集单体电压，只对最大电压和最小电压单体进行充放电控制。当某个工作周期中，出现2个或多个相同最大电压(最小电压)的储能单体时，为了保证电路仍然正常工作，通过控制开关对所有相同最大电压(最小电压)的储能单体依次交替进行放电(充电)。从而使得具有相同电压的储能单体的电压一致下降(上升)，因此为了确保精确的对目标均衡单体进行充放电控制，图8给出了该均衡电路的控制策略。

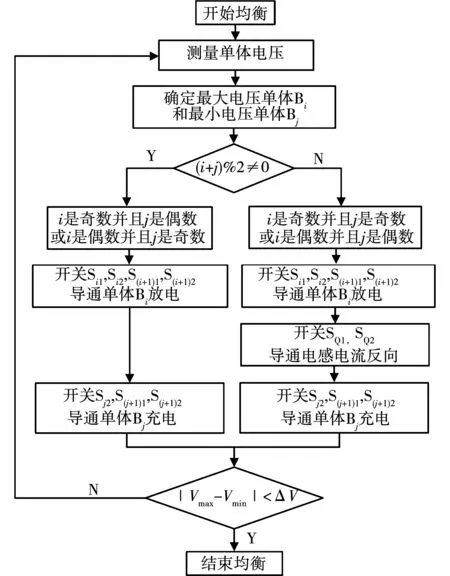
图8 均衡电路控制策略Fig.8 Control strategy of equalization circuit

4 均衡电路的速度对比分析

均衡速度是衡量电压均衡电路一项比较重要的指标，通常来说，均衡器的额定功率越高，均衡时间越短，那么均衡速度也就越快。但是当均衡额定功率一定时，均衡周期数是决定均衡速度的关键因素[16]。当N个电压不均衡储能单体串联时，为了达到均衡目标，所需要的平均均衡周期数可定义为

(14)

其中：y是从放电单体向充电单体转移能量所需的总的均衡周期数；x是所有可能不均衡状态的数目，对于上述假设，则有

x=N(N-1)。

(15)

在相邻单体-单体型均衡电路中，当放电单体和充电单体处于不相邻位置时，则需要多次周期能量转移，才能实现最终均衡目标。表2给出了相邻单体-单体型均衡电路中能量转移均衡周期与均压单体的位置分布关系。

由表2可知，N个串联电池组可能出现的所有需要的能量转移周期数之和表达式为

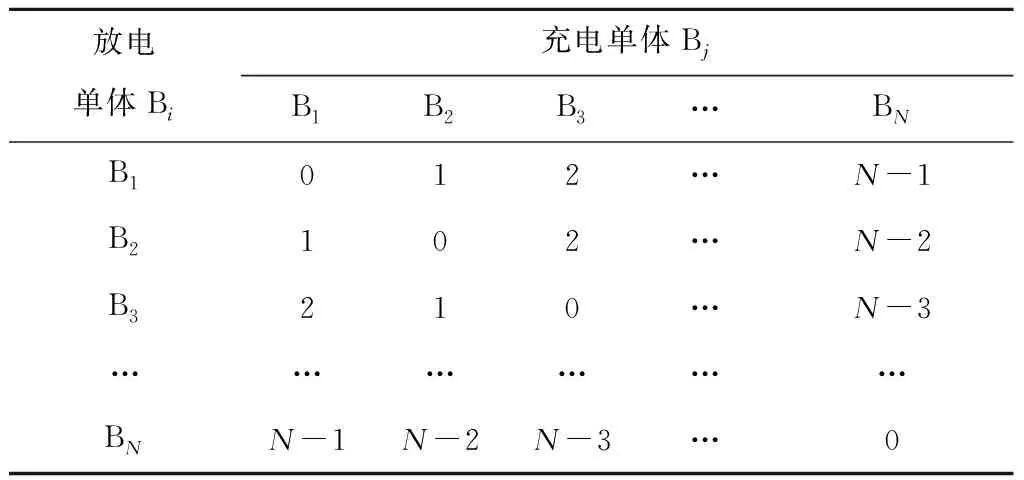
表2 相邻单体-单体型均压电路能量转移周期

(16)

因此，相邻单体-单体型均压电路能量转移的平均周期为

(17)

对于本文所提出的基于LC单元的双向单体-单体电压均衡电路，属于直接单体-单体型均衡电路，表3给出了该均衡电路的能量转移均衡周期与均压单体的位置分布关系。

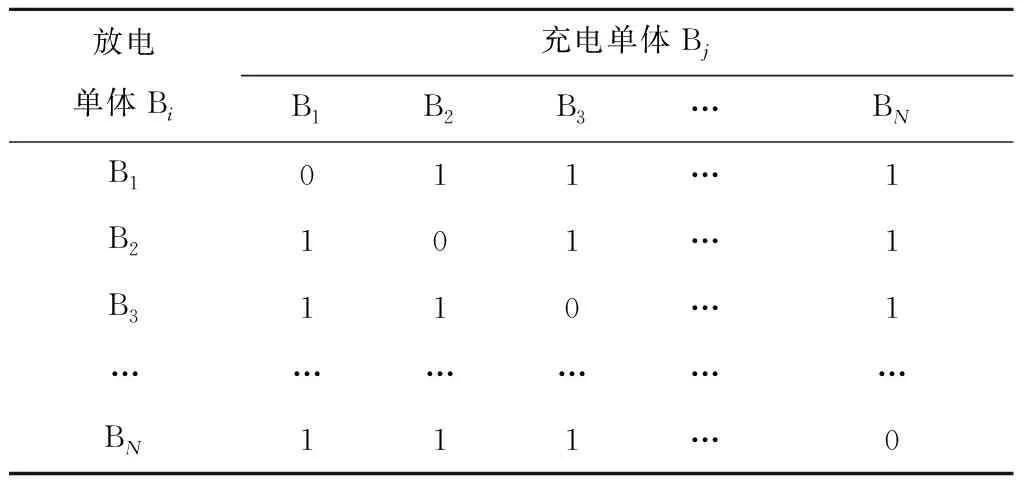
表3 直接单体-单体型均压电路能量转移周期

由表3可知，对于N个串联储能单元组可能出现的所有需要的能量转移周期数之和表达式为

y=N(N-1)。

(18)

因此，本文提出的基于LC单元的双向单体-单体均衡电路能量转移的平均周期为

(19)

根据式(17)、式(19)，两种均衡电路的平均转移周期数如图9所示，随着串联储能单体数量的增加，相邻单体-单体型均衡电路能量转移的平均周期会越来越多。但是所提出的基于LC单元的双向单体-单体均衡电路能量转移的平均周期并不会随着串联储能单体数量增加而增加，因此当串联储能单体数量较大时，该电路在速度方面具有较明显的优势。

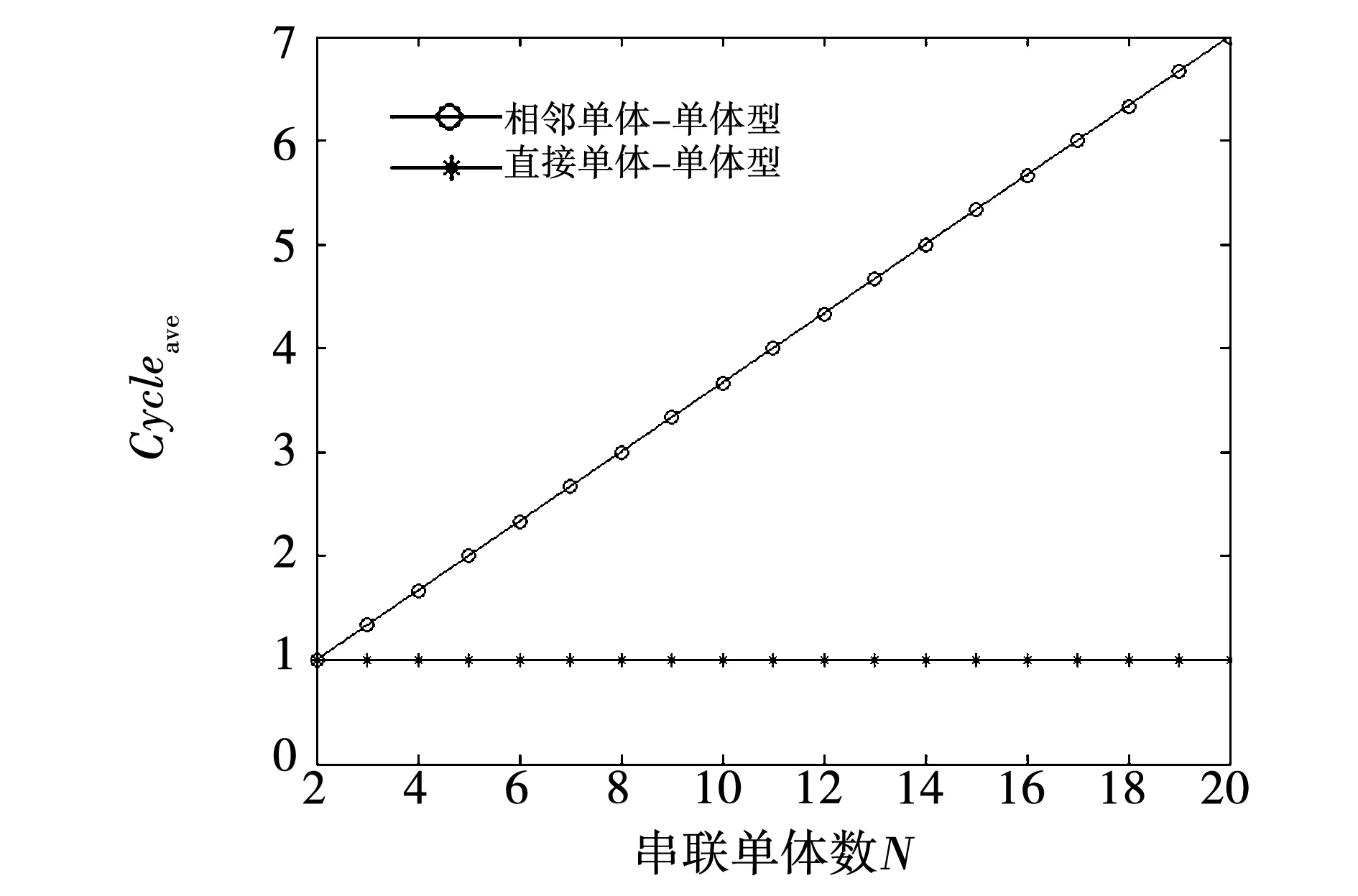
图9 不同电路的平均能量转移周期数对比Fig.9 Comparison of average energy transfer cycles of different circuits

5 实验验证

为了验证本文提出的均衡电路理论分析，搭建了一台基于4个串联储能单体的双向单体-单体均衡电路样机，储能单体选择为超级电容器。其主要实验电路参数如表4所示，实验平台如图10所示。

图10 实验平台实物Fig.10 Photograph of experimental prototype

表4 实验参数

实验中选择4个额定电压为2.7 V的700 F的超级电容器作为电压均衡储能单元，分别进行了静态下的静置均衡和动态下的充电均衡实验验证。静置均衡时分别对不同初始电压分布状态进行了实验验证，动态均衡时以0.3 A的电流对串联超级电容组进行恒流充电均衡。

图11所示为超级电容器在不同初始电压分布的均衡实验曲线。图11(a)为初始电压VSC3>VSC1>VSC4>VSC2(2.5、2.4、2.3、1.9 V)情况下的电压均衡曲线，由实验结果可以看出整个均衡过程分为3个阶段。在第一阶段中，电压VSC3最大，电压VSC2最小，能量从SC3向SC2转移，此时均衡电路工作在状态一；当均衡过程进入第二阶段时，电压VSC3下降到和VSC1一致，此时能量从SC1和SC3共同向SC2转移，此时均衡电路在工作状态一和状态二交替进行；当均衡过程进入第三阶段时，电压VSC1、VSC3下降到和VSC4一致，此时能量从SC1、SC3、SC4共同向SC2转移，均衡电路在工作状态一和状态二交替进行。随着均衡过程的进行，当最大电压差达到设定的5 mV压差范围内时，电路停止工作，均衡结束。

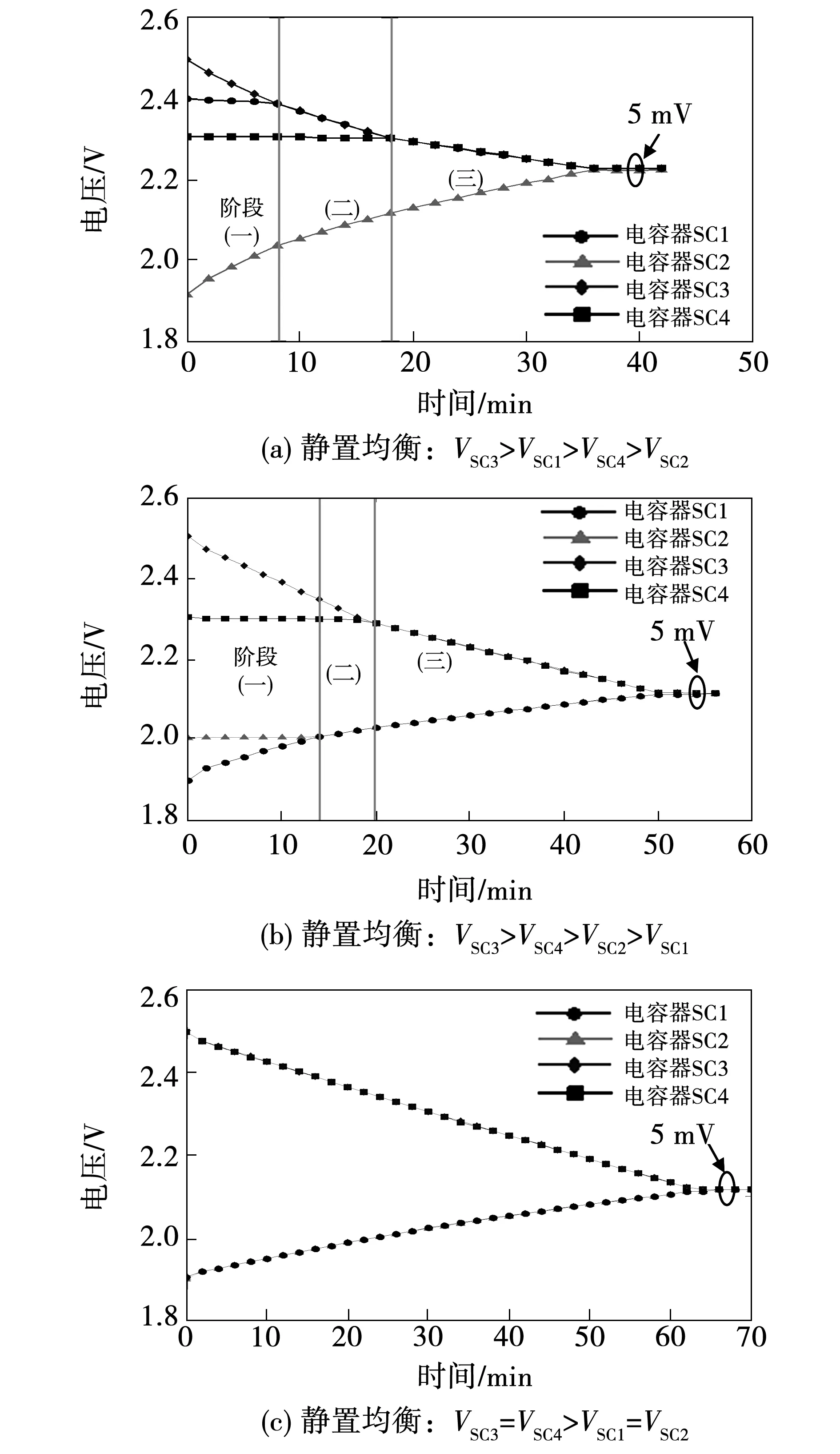
图11 不同初始电压分布的实验曲线Fig.11 Experimental waveforms with different initial voltage

图11(b)为初始电压VSC3>VSC4>VSC2>VSC1(2.5、2.3、2.0、1.9 V)的情况下的电压均衡曲线，同样整个均衡过程可分为3个阶段。在第一阶段中，电压VSC3最大，电压VSC1最小，能量从SC3向SC1转移，此时均衡电路工作在状态二；当均衡过程进入第二阶段时，电压VSC1上升到和VSC2一致，此时能量从SC3向SC1、SC2转移，均衡电路在工作状态一和状态二交替进行；当均衡过程进入第三阶段时，电压VSC3下降到和VSC4一致，此时能量从SC3、SC4向SC1、SC2转移，均衡电路在工作状态一和状态二交替进行。随着均衡过程的进行，当最大电压差达到设定的5 mV压差范围内时，电路停止工作，均衡结束。

图11(c)为初始电压VSC3=VSC4>VSC1=VSC2(2.5、2.5、1.9、1.9 V)的情况下的电压均衡曲线，整个均衡过程。电路在工作状态一和状态二交替进行，能量从SC3、SC4向SC1、SC2转移，直到最大电压差达到设定的5 mV压差范围内时，电路停止工作，均衡结束。

为了验证该电路的动态均衡性能，实验进行了超级电容器充电过程中的电压均衡实验。图12为充电状态下的电压均衡曲线，可以看出，随着均衡过程和充电过程的同时进行，所有超级电容器电压均呈增加状态，同时最大电压差也逐渐减小，直至小于设定的压差范围，最后停止均衡，充电继续。

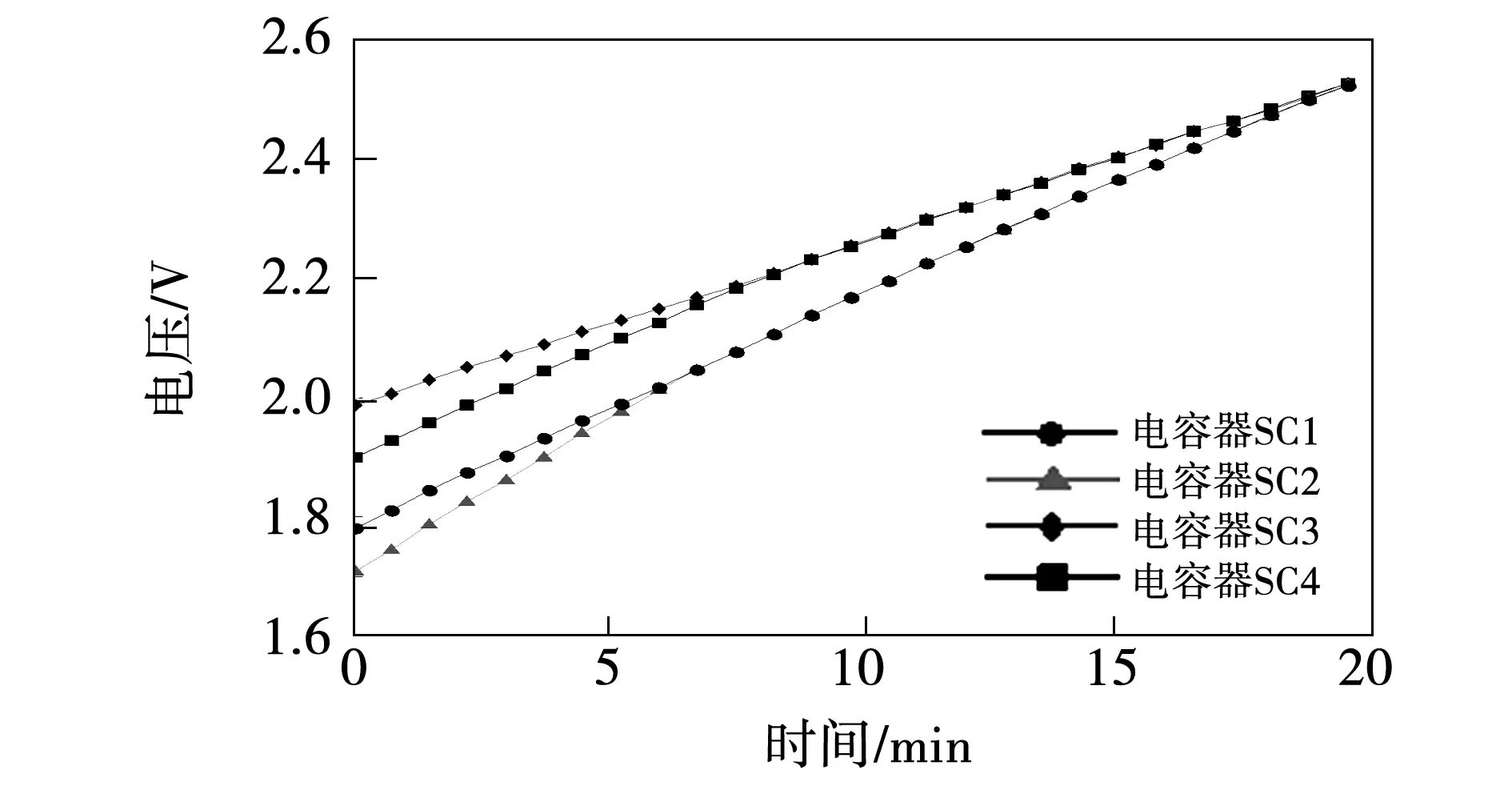
图12 充电状态下电压曲线Fig.12 Voltage equalization curve under charging state

图13给出了实验过程中的控制信号和电感电流波形，图13(a)为电路工作在状态一时的波形，可以看出在每个周期中，电感电流先线性上升到最大值，再线性下降降至0。图13(b)为电路工作在状态二时的波形，可以看出在每个周期中，电感电流先线性上升到最大值，然后和电容谐振半个周期后，电感电流变为反向最大值，然后再线性下降至0。图13(c)是工作状态一和工作状态二交替进行的工作波形。以上所有实验结果均与理论分析一致。

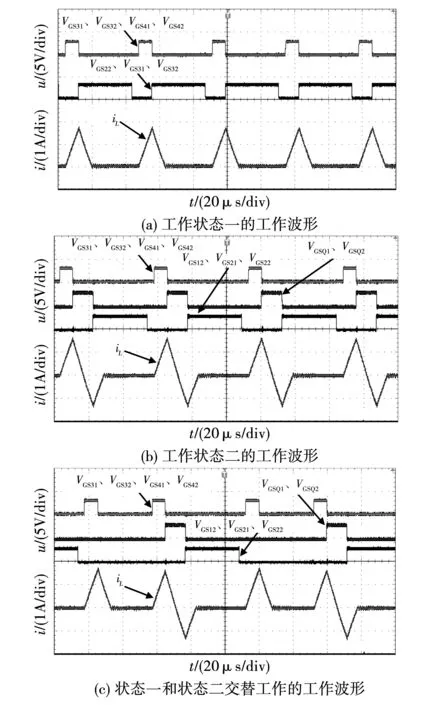
图13 实验波形Fig.13 Experimental waveforms

6 结 论

本文提出了一种基于LC单元的双向电压均衡电路，对均衡电路工作原理进行了理论分析，控制策略及特性对比分析。相对于传统的单体-单体型电压均衡电路，所提的电压均衡电路优点在于缩小了能量传输路径以及减小磁性元件数量，同时该电路的控制策略保证了电路的精确均衡。最后通过设计实验样机，进行了串联超级电容组在静态和动态下的均衡实验，实验结果验证了理论分析的正确性。