高功率因数无电解电容IPMSM驱动系统电流跟踪控制策略
梁晨,章玮
(浙江大学 电气工程学院,杭州 310027)
0 引 言
内置式永磁同步电机(interior permanent synchronous motor,IPMSM)具有高效率,高功率密度等优点。传统IPMSM驱动系统为保证稳定的直流母线电压,一般采用上百微法的电解电容。然而电解电容体积大,寿命短等特点影响了驱动系统的可靠性。同时为满足网侧谐波要求,传统电解电容驱动系统需添加功率因数校正电路(PFC),这又增加了系统成本与体积。因此,采用薄膜电容代替电解电容,同时省去PFC,利用控制策略得到网侧高功率因数的研究引起了广泛关注。
无电解电容驱动系统母线电容减小导致网侧二极管导通角增大,这为实现网侧高功率因数提供了条件。文献[1-2]采用转速环-功率环-电流环控制结构,在功率环使用重复控制器控制逆变器输出功率以实现网侧高功率因数。文献[3-4]将功率环的重复控制器替换为比例谐振控制器,相较于重复控制器,比例谐振控制器需要整定的参数少,但只能跟踪单一频率的正弦信号。由于功率环参数难整定且对系统稳定性影响较大,为简化系统提高系统稳定性,文献[5]提出根据系统方程及电压约束条件离线计算整个周期的最优电流指令轨迹,由于这种方法只能针对系统特定运行状态制作电流指令表,实际应用有一定局限。为了在线计算电流指令,文献[6]简化系统方程,利用逆变器输出功率与电机q轴电流关系在线计算q轴电流指令,并为补偿简化方程带来的影响,调整了q轴电流指令形状,削弱了电流指令峰值。文献[7]将功率环输出用于修正q轴电流指令以补偿简化系统方程带来的影响。文献[8]则在简化的q轴电流指令上叠加了一个基于母线电压变化的正弦量以修正q轴电流指令。由于以上在线计算电流指令的控制策略并非基于完整的系统方程,采取各种修正措施只能使电流指令接近最优值。
针对以上问题,本文在分析系统方程敛散性的基础上,通过离散逆变器输出功率方程在线计算电机q轴理论最优电流指令轨迹。并通过对电流指令轨迹进行幅值与相位的补偿,使电流环采用PI控制器就能实现对电流指令轨迹的良好跟踪效果。在保证网侧高功率因数的基础上简化了控制系统,最后用仿真与实验验证了此控制策略的有效性。
1 无电解电容控制系统分析
单相无电解电容IPMSM驱动系统由不控整流桥,母线薄膜电容,逆变器与电机构成。拓扑图如图1所示。
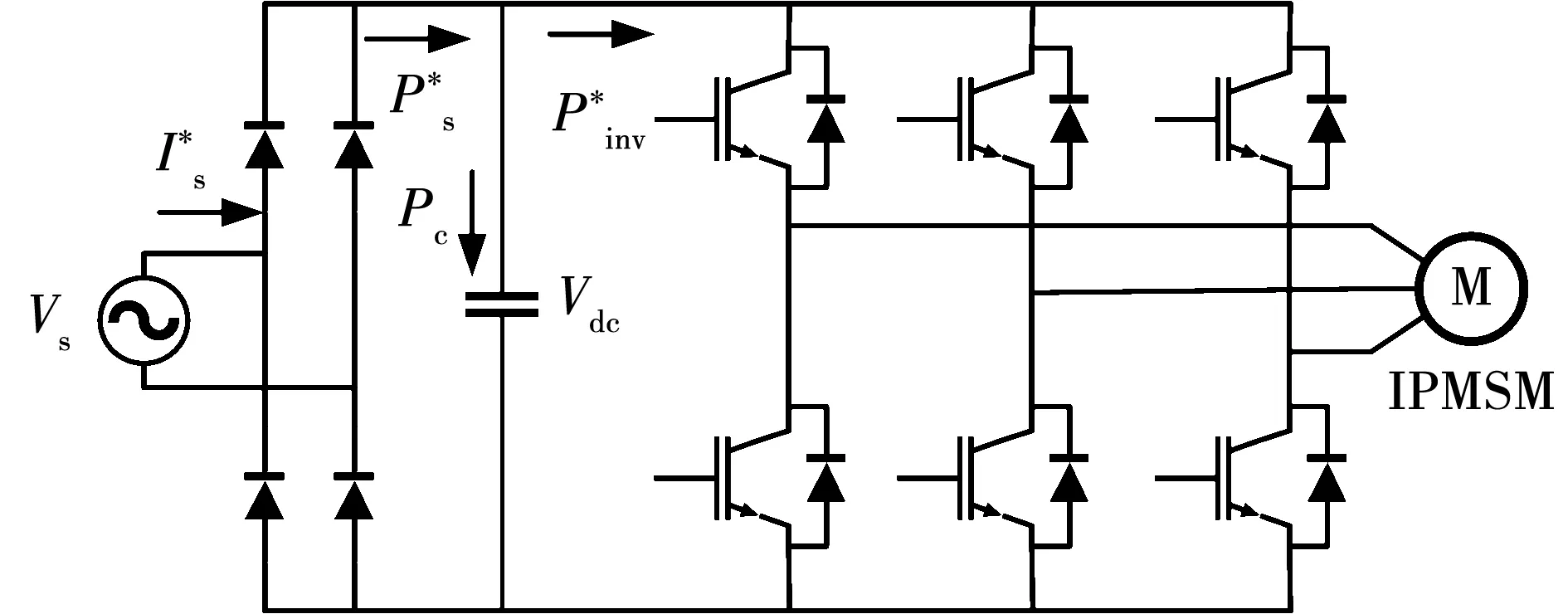
图1 无电解电容IPMSM驱动系统的拓扑结构Fig.1 Topology of electrolytic capacitor-less IPMSM drive system
Vs=Vsmsinωst;
(1)
(2)
Vdc=Vsm|sinωst|。
(3)
(4)
式中:Cdc为母线薄膜电容容量;sgn(x)为符号函数。理想网侧输入功率为
(5)
由式(3)、式(4)得到电容功率为
(6)
由功率平衡关系可得理想逆变器输出功率为
(7)
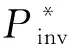
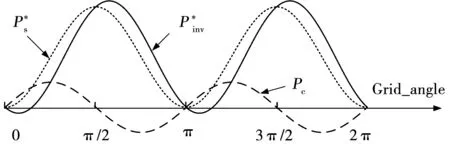
图2 功率关系图Fig.2 Power diagram
为控制逆变器输出功率为理想波形,分析逆变器输出功率与电机电流关系。永磁同步电机在d-q坐标系下的电压方程,即
(8)
(9)
式中:ud、uq分别为d、q轴电压分量;R为定子电阻;id、iq分别为d、q轴电流分量;Ld、Lq分别为电机d、q轴电感;ωe为转子电角速度;φf为永磁体磁链。逆变器输出功率用电机d-q坐标系下的电压电流表示为
Pinv=1.5(udid+uqiq)。
(10)
将式(8)、式(9)代入式(10)得逆变器输出功率与电机电流关系为
ωe[(Ld-Lq)id+φf]iq}。
(11)
有文献通过式(11)离线计算最优电流指令[5],但由于离线计算只能针对系统特定运行状态制作电流指令表,其实用性有一定限制。为解决这个问题,基于系统方程的敛散性分析,通过对式(11)进行离散化处理,在线计算出电机最优电流指令轨迹,并通过控制电机电流跟踪最优指令轨迹获得网侧高功率因数。
2 高功率因数下电流控制策略
2.1 d轴电流控制策略
母线采用薄膜电容导致母线电压大幅度波动,需采用弱磁控制保证电机稳定运行。电机d-q轴给定电压需满足电压约束条件:
(12)
由于母线电压以二倍网侧频率波动,难以实时满足电压约束条件,因此以一个母线电压周期内平均电压作为约束条件[9]。将式(12)在一个母线电压周期内积分,得到平均电压约束条件:
(13)
式中Tg为网侧电压周期,在工频50 Hz的条件下,Tg=20 ms。
由式(13)所得d轴弱磁电流指令计算框图如图3所示,图中滤波器采用窗口长度为一个周期的滑窗滤波器以得到平均电压差值。当电机电压平均值大于母线电压平均值时,PI控制器输入为负,d轴弱磁电流反向增大使电机平均电压减小,实现了电压的闭环控制。为防止出现积分饱和现象,采用遇限削弱积分PI控制器,其输出上限为0,输出下限为d轴弱磁电流最小值。考虑到电机绕组安全,d轴弱磁电流指令值不能过小,弱磁电流指令最小值为
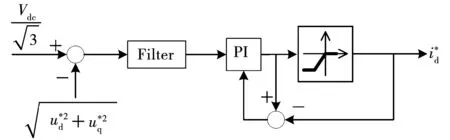
图3 d轴电流指令计算框图Fig.3 Block diagram of calculating d-axis reference current
(14)
式中:INm为电机最大允许电流;iq_rms为电机q轴电流有效值。
系统稳定运行时PI控制器输入为0,输出为常数,这使得d轴弱磁电流指令为恒值,方便了弱磁电流的控制并且消去了逆变器输出功率表达式(11)中的d轴电流微分项,减小了逆变器输出功率与电机d轴电流的耦合。
2.2 q轴电流控制策略
消去逆变器输出功率表达式(11)中d轴电流微分项,逆变器输出功率与电机q轴电流关系可表示为
ωe[(Ld-Lq)id+φf]iq}。
(15)
将式(15)离散化处理后,得控制系统中q轴电流指令计算表达式为
(16)
传统PI控制器在对时变参数进行控制时会产生跟踪误差。但由于q轴电流指令轨迹近似频率恒定的正弦波,采用PI控制器产生的幅值和相位的误差为恒定值,因此可采用PI控制器并对电流指令轨迹进行幅值和相位的补偿,即可保证良好的跟踪效果。
为计算补偿值,需对q轴电流环进行分析。将q轴电压方程式(9)进行拉氏变换,并将耦合反电势项作为干扰,画出q轴传递函数框图如图4所示。
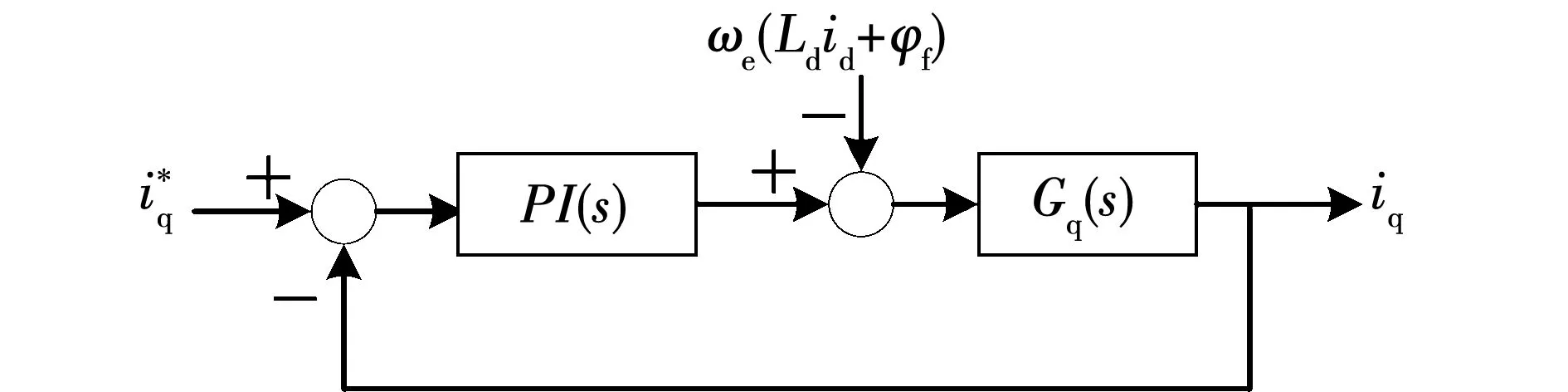
图4 q轴传递函数框图Fig.4 Block diagram of q-axis transfer function
框图中PI控制器传递函数为
(17)
式中:Kp和Ki分别表示PI控制器的比例系数和积分系数。将d-q轴解耦消去反电势干扰项后PI控制器输出的q轴电压给定对q轴电流的传递函数为
(18)
(19)
A=abs[P(j100·2π)]。
(20)
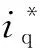
B=angle[P(j100·2π)]。
(21)
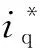
(22)
2.3 Q轴电流指令轨迹收敛性分析
为确保基于式(16)得出的电流指令轨迹能使电机稳定运行,需对电流指令轨迹的敛散性进行分析,将式(15)表示为iq的状态变量方程,即
(23)
令diq/dt等于0求其平衡点,得对应一元二次方程为
(24)
内嵌式永磁同步电机Ld小于Lq且系统控制id为负值,可知式(24)的一次项系数与二次项系数恒正。根据韦达定理,在一次项系数与二次项系数恒正的情况下:常数项为正时,两个根均为负;常数项为负时,两个根一正一负。式(24)根为负表示电流指令平衡点为负值,这时电机工作在制动状态。为保证电机正常运行,需确保电流指令轨迹收敛于正的平衡点,所以式(24)的常数项为负是电流指令轨迹正确收敛的一个必要条件。由式(23)得常数项为负时的电流指令轨迹相平面分析图如图5所示,其计算所需参数如表1所示。由相平面分析可知电流指令轨迹收敛于正的平衡点的另一个条件是电流指令轨迹初值为正。

图5 常数项为负的相平面图Fig.5 Phase plane diagram with negative constant term
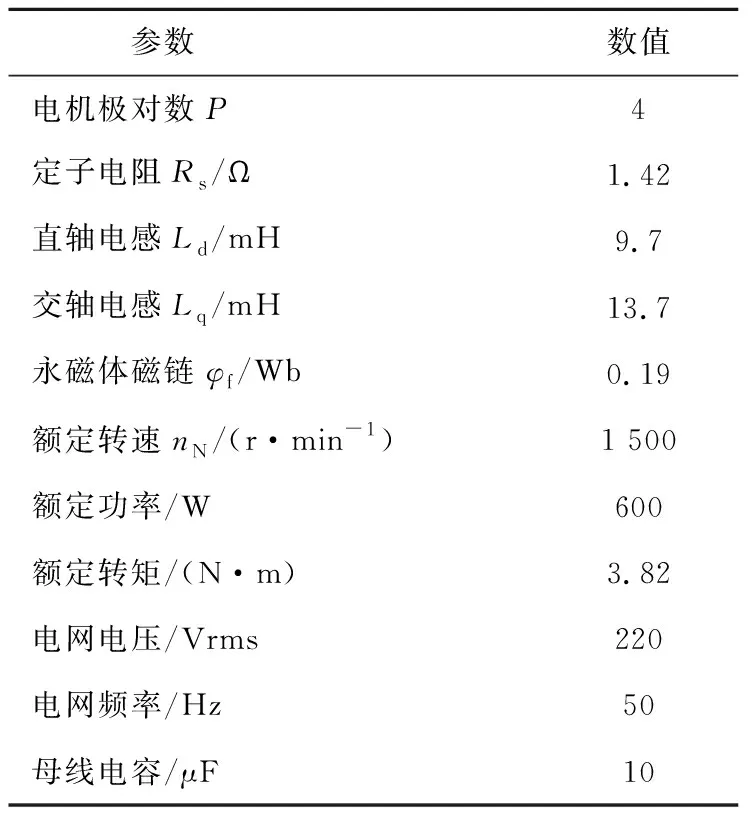
表1 电机参数
综上分析,电流指令轨迹正确收敛的条件为式(24)的常数项为负且电流指令初始值为正。由于理想逆变器输出功率以二倍网侧频率波动,当理想逆变器输出功率降低至式(24)的常数项为正后,电流指令轨迹不能收敛到正的平衡点,需采用其他方式计算电流指令轨迹。由于此时理想逆变器输出功率小,可忽略式(15)中的q轴电阻功率项及电磁储能项,得到接近最优值的q轴电流指令轨迹为
(25)
当理想逆变器输出功率增大至常数项为负时,式(25)所得q轴电流指令为正值,将式(25)作为电流指令轨迹初始值,电流指令轨迹能够正确收敛。
2.4 系统控制框图
基于以上分析的高功率因数控制策略框图如图6所示。d轴电流指令经过PI控制器输出d轴给定电压。q轴转速环输出作为理想网侧输入功率的幅值,结合网侧电压相位ωst得到理想网侧输入功率,其中网侧电压相位ωst由二阶广义积分锁相环(SOGI-PLL)得到[10]。再由理想网侧输入功率与母线电容功率生成理想逆变器输出功率,经q轴电流指令生成模块生成q轴电流指令,最后通过PI控制器输出q轴给定电压。算出的d-q轴给定电压经过电压限幅模块与坐标变换模块输出到SVPWM模块。
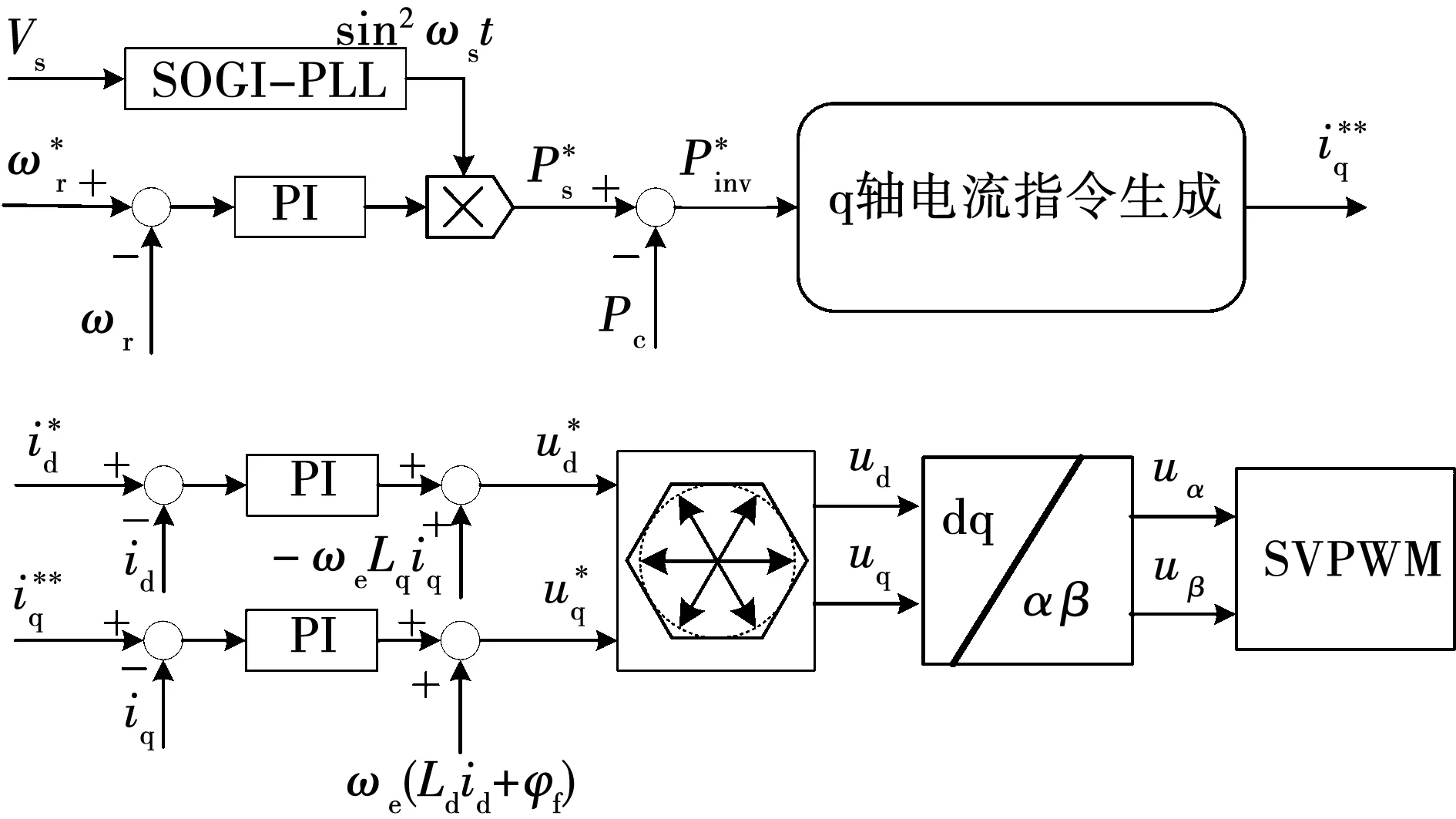
图6 控制策略框图Fig.6 Block diagram of control strategy
3 仿真与实验分析
为验证上述控制策略的有效性,在MATLAB/Simulink中进行仿真分析并在实际平台进行实验验证。仿真与实验的系统参数相同,如表1所示。
母线电容过小会导致母线电压尖峰增大,母线电容过大会减小网侧二极管导通角减小。为合理选择母线电容,基于文献[11]的解析分析方法,综合考虑电机功率要求与输入功率因数要求后,选取10 μF母线电容。无电解电容系统运行在额定转速下需要较大的弱磁电流来保证电机稳定高速运行及网侧高功率因数,且由于q轴电流呈二倍网侧频率波动,相同负载转矩下的无电解电容系统q轴电流有效值比传统电解电容系统q轴电流有效值更大。以上原因导致额定功率下的电机电流有效值可能超过额定电流值。考虑到这些因素,将无电解电容驱动系统仿真及实验中电机的目标转速、负载转矩设置为额定值的80%,即1 200 r/min、3 N·m。
结合式(16)与式(25)得到q轴电流指令轨迹如图7所示,图中虚线以上为电流指令轨迹收敛区域,虚线以下为非收敛区域。
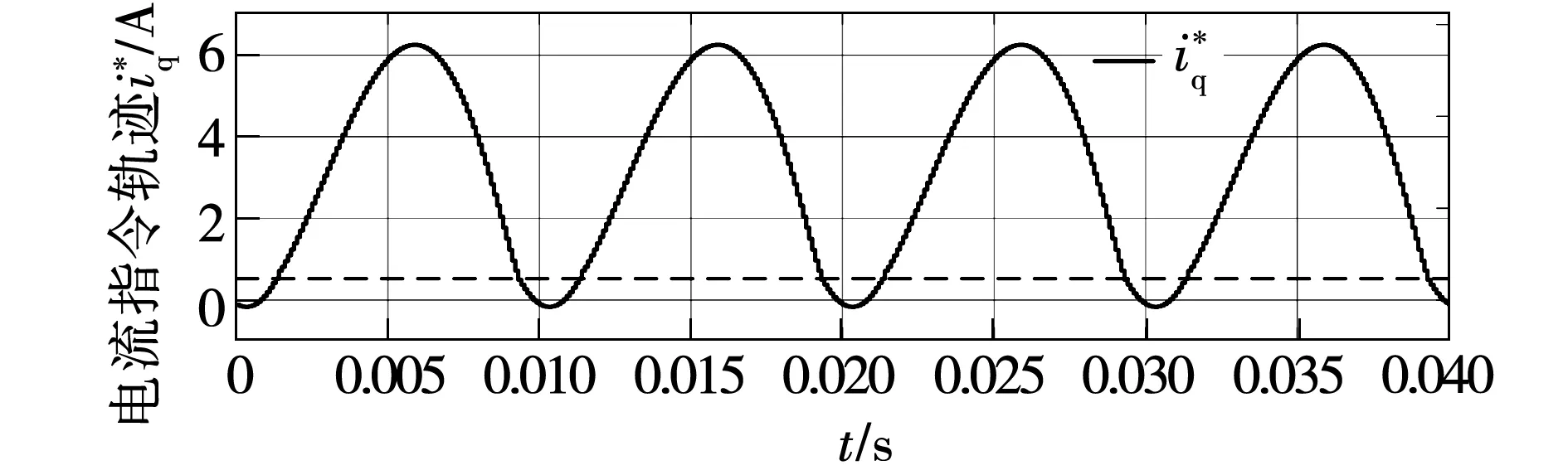
图7 电流指令轨迹Fig.7 Reference current trajectory
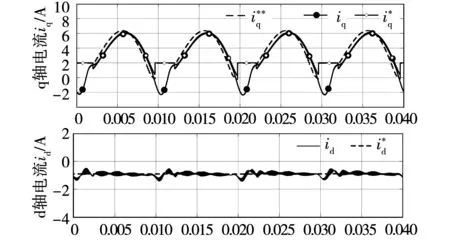
图8 d-q轴电流仿真波形Fig.8 Simulation waveforms of d-q axis current
母线电压深度跌落时失去对电机电流的控制能力,q轴电流在反电势作用下跌落至负值,导致能量由电机流向母线电容,使母线电压出现尖峰,网侧二极管关断。为增大网侧二极管导通角以提高网侧功率因数,在母线电压出现尖峰时将q轴电流指令设置为一较大值,使母线电容能量快速回流至电机,加快网侧二极管导通。
仿真中逆变器功率、母线电压、网侧输入电流波形如图9所示。采用薄膜电容后网侧二极管导通角增大,母线电压以二倍网侧频率波动。在网侧二极管导通期间,逆变器输出功率、网侧输入电流的波形与理想值基本重合,验证了控制策略有效性。

图9 网侧功率电压电流仿真波形Fig.9 Simulation waveform of power voltage and current at grid side
以图1拓扑结构搭建实验平台验证控制策略实际效果,如图10所示。控制芯片采用STM32G431,实验数据由控制芯片输出pwm信号至示波器后保存所得。实验中各系统参数与仿真一致,如表1所示。

图10 实验平台Fig.10 Experimental platform
电机转速、负载转矩设置与仿真相同,即1 200 r/min、3 N·m。d-q轴实验电流波形如图11所示,与仿真基本一致。q轴电流呈二倍网侧频率波动且在网侧二极管导通期间电流跟踪效果良好,验证了电流指令补偿策略的有效性。电机稳定运行下的d轴电流指令基本为常量。

图11 d-q轴电流实验波形Fig.11 Experimental waveforms of d-q axis current
逆变器输出功率与母线电压的实验波形如图12所示,与仿真波形基本一致。网侧二极管导通期间逆变器实际输出功率与理想输出功率波形基本重合,验证了控制策略的有效性。
为验证多工况下控制策略的有效性,实验中对电机转速高低,负值大小进行组合,设置了a、b、c、d四种不同工况。设置a工况转速750 r/min,负载3 N·m;b工况转速750 r/min,负载1.8 N·m;c工况转速1 200 r/min,负载1.8 N·m;d工况转速1 200 r/min,负载3 N·m。a、b、c、d四种工况切换时的电机转速波形图及每个工况下的网侧输入电流波形如图13所示。
将图13中4种工况下实验波形进行分析得到功率因数依次为0.972 1、0.979 1、0.982 3、0.985 7;谐波畸变率依次为0.234 2、0.203 5、0.175 4、0.178 6。可见此控制策略可以有效实现系统的网侧高功率因数、低电流谐波运行。将网侧输入电流各次谐波在4种工况下的最大值与IEC61000-3-2标准比较,其结果均符合IEC61000-3-2的A类标准,如图14所示。
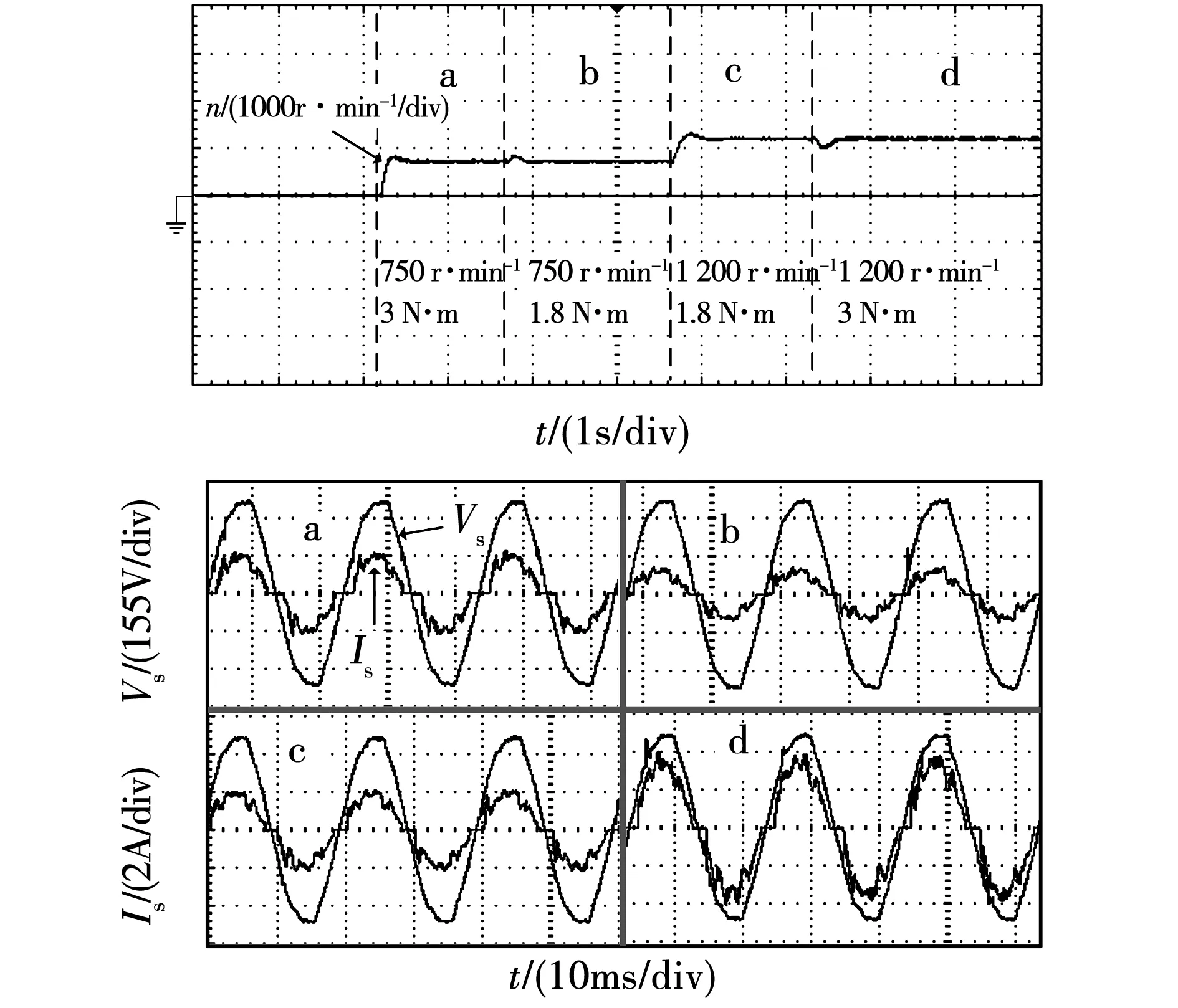
图13 转速与网侧输入电流实验波形Fig.13 Experimental waveforms of speed and grid side input current

图14 输入电流谐波幅值Fig.14 Harmonic amplitude of input current
4 结 论
本文研究了一种高功率因数无电解电容永磁同步电机控制策略。基于系统方程的敛散性分析,通过离散系统方程在线计算最优电流指令轨迹。并基于电机电流环的分析,采用PI控制器结合幅值与相位的补偿实现对二倍工频电流指令的跟踪,简化了控制方法。仿真与实验均验证了控制策略的有效性。该方法进一步研究了无电解电容控制系统下的高性能控制策略,具有控制器简单、稳定性高等优势,有一定实用价值。

