面向切屑形成过程的瞬时滚削力模型研究
丁国龙 叶梦传 向 华 杨春兰
1.湖北工业大学机械工程学院,武汉,430068 2.华中科技大学国家数控系统工程技术研究中心,武汉,430074 3.秦川集团(西安)技术研究院有限公司,西安,710016
0 引言
高速干切滚齿是一种新型的齿轮滚切加工工艺,滚刀形状和结构、工件材料、加工各轴速度等参数会直接影响瞬时滚齿切削力(简称“滚削力”)的变化。建立滚齿加工的运动学模型,对瞬时滚削力进行研究,一方面在保证加工安全的前提下能提高加工效率,另一方面将理论模型融入数控系统,使数控机床具备自主决策优化工艺参数的功能,提高了机床智能化程度。
滚齿切削力通常是通过大量滚削力实验数据,采用不同理论拟合的经验公式进行拟合计算[1-2],只能计算平均滚削力,不适用于瞬时切削力的计算。目前,国内外许多学者对齿轮加工仿真和切削力模型进行了研究。丁国龙等[3]对SolidWorks进行二次开发,模拟了复杂非圆齿实体的加工过程;SABKHI等[4]、TAPOGLOU等[5]、张荣闯等[6]基于CAD建立滚齿加工空间运动模型,获取加工切屑几何特征;周力等[7]、吕盈等[8]、刘佳等[9]使用等距分割法提取切屑表面点,分别采用解析法和有限单元法计算单齿切削力;赵大兴等[10]、邓志刚等[11]建立了插齿切削运动模型,利用MATLAB计算投影面积,得到主切削力;孙军等[12]、陈永鹏等[13]基于切削微元建立滚刀瞬时切削力模型。在滚削力测量方法上,张荣闯等[6]在机床主轴上安装旋转测力仪工装测量滚削力;ALAZAR等[14]将间距120°布置三个压电测力仪无线遥测装置安装在机床的工件轴上测量滚削力。以上方法均需要在机床上安装测力仪工装,通用性不好。
本文建立干切滚齿加工运动模型,提取未变形仿真切屑。在建立瞬时滚削力模型的基础上研究工艺参数对瞬时滚削力的影响,分析滚削力的波动特性,提出降低滚削力波动的措施,并在YK3126CNC滚齿机上进行了加工验证。
1 滚齿加工运动模型
1.1 空间坐标系定义与转换
数控滚齿机共有六个伺服轴,两个旋转轴A轴(刀架回转轴)、C轴(工件回转轴),三个直线运动轴X轴(径向进刀轴)、Y轴(切向串刀轴)、Z轴(轴向走刀轴),另有一个伺服主轴B轴(滚刀回转轴)。各轴的正方向如图1所示。

图1 数控滚齿机伺服轴定义Fig.1 Definition of servo shaft
定义坐标系Sr(Orxryrzr)与机床固连,坐标系Sg(Ogxgygzg)与滚刀固连,坐标系Sh(Ohxhyhzh)与工件固连。开始加工为t0时刻,t1为加工过程中的某一时刻。在t1时刻,滚刀转动ωt1,工件转动φt1,滚刀沿工件轴向走刀位移为ft1,此刻滚刀坐标系与工件坐标系分别用Sg1(Og1xg1yg1zg1)和Sh1(Oh1xh1yh1zh1)表示。
设滚刀的安装角为γ,安装高度为hg,分度圆直径为d1,工件安装高度为hh,滚刀与工件径向进给方向的中心距为lx,Og与Orxrzr平面的距离为lyg,Oh与Orxrzr平面的距离为lyh。各坐标轴定义如图2所示。

图2 坐标系转换关系Fig.2 Transformation between coordinate systems
Sg1与Sg的坐标变换矩阵为M1;Sg与Sr的坐标变换矩阵为M2;Sr与Sh的坐标变换矩阵为M3;Sh与Sh1的坐标变换矩阵为M4。设滚刀上任意一点j在t1时刻Sg1坐标系下坐标可以用Pgj表示,Sh1下空间坐标可以用Phj(t1)表示,则
Phj(t1)=M1M2M3M4Pgj
(1)
1.2 滚刀刀齿齿廓离散化
滚刀刀齿切削刃由前刀面上的两个侧刃、一个顶刃和两个圆弧刃组成,因此,可将滚刀刀齿(空间螺旋曲面)的研究简化为对刀齿前刀面齿廓(平面曲线)的研究。刀齿编号如图3所示,以滚刀上第一个与工件展成运动的刀齿为参考刀齿,编号为0,顺着滚刀螺旋线沿Ohxh轴正方向的刀齿依次编号1,2,…,i1,负方向编号依次为-1,-2,…,i0。设i号表示任意刀齿,i号刀齿前刀面与参考刀齿前刀面之间的夹角和沿Ohyh方向的距离可以用θi、Li表示,其中k为滚刀容屑槽数,m为滚刀模数,有
(2)
(3)
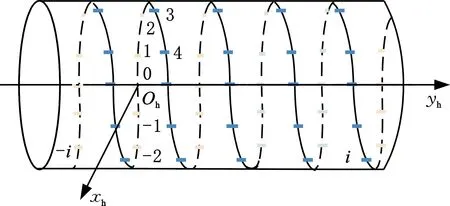
图3 滚刀刀齿编号Fig.3 Hob tooth number
参考刀齿齿廓坐标系如图4所示,齿廓分为ab、bc、cd、de四段,xg在不同区间取值如表1所示,齿廓方程可以用分段函数f(xg)表示,由于齿廓关于Ogyg对称,故分布在第一象限的齿廓方程可以用g(xg)表示:
(4)
g(xg)=
(5)
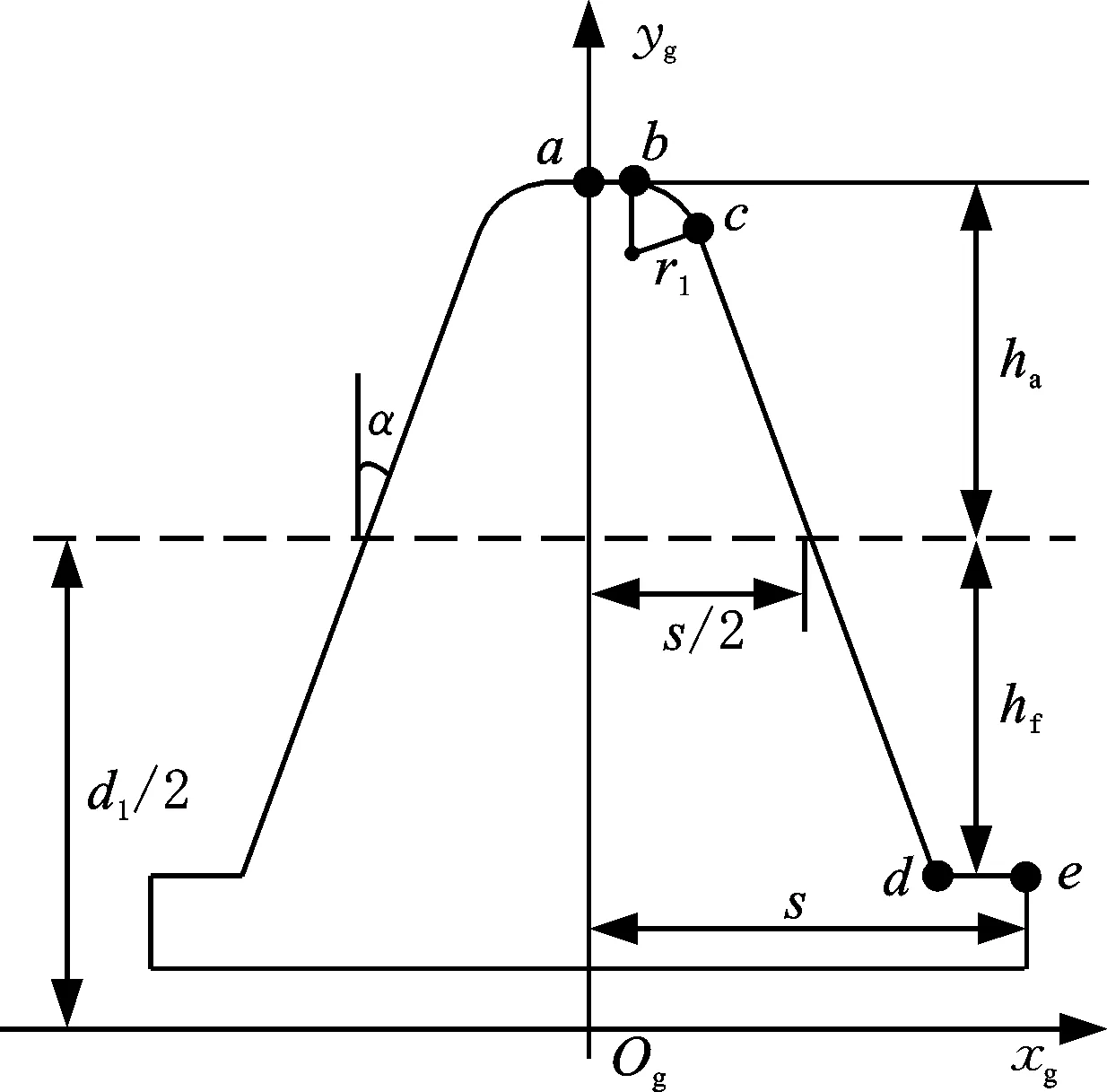
图4 参考刀齿齿廓坐标系Fig.4 Reference cutter tooth profile coordinate system

表1 xg不同区间取值表Tab.1 Values for xg different intervals
式中,r1为滚刀齿顶过渡圆半径;α为滚刀齿形角;ha为滚刀齿顶高,ha=1.25m;hf为滚刀齿根高,hf=1.25m;s为轴向齿厚。
参考刀齿的齿廓沿着Ogxg轴的正方向等距离散为ns个齿廓坐标点,齿廓曲线可以用空间坐标点矩阵Hg来表示:
Hg=
(6)
其中,ks为相邻齿廓点的间距,ks=2s/ns。
滚刀上任意刀齿i的齿廓坐标点矩阵Hgi可以表示为
(7)
1.3 刀齿切削轨迹离散化
设滚刀主轴转速为nB,工件轴转速为nC,进刀量为ap,走刀速度为af,滚刀头数为N。
ωt1、φt1、ft1和lx计算如下:
(8)
(9)
(10)
(11)
(12)
其中,ra为工件齿顶圆半径;z为工件齿数;用齿廓坐标点矩阵Hgi代替Pgj,将式(7)~式(12)代入式(1)中,求得任意时刻t1在坐标系Sh1下任意刀齿i的齿廓坐标矩阵Hhi(t1):
Hhi(t1)=M1M2M3M4Hgi
(13)
如图5所示,以加工一个齿槽为例,假设有np个刀齿参与切削,在齿槽切入点P1位置展成切削的刀齿为0号刀齿,工件自转的同时滚刀自转,依次1,2,…,np号刀齿展成切削。当P1转动φ0至P2位置,刀齿完成齿槽的展成切削。sp为P1转动至P2的弧长,有如下关系:
(14)
sp=rpφ0
(15)
(16)
w=1.25m-r1(1-sinα)
(17)
式中,rp为工件分度圆半径;p为滚刀轴向齿距;L、w为计算中间变量。

图5 齿槽切削图Fig.5 Groove cutting
切削一个齿槽参与的刀齿数np为
(18)
以时间t为驱动变量,将t离散化处理,分为等间距nq份,时间间隔为Δt,任意刀齿i的运动轨迹用矩阵Hi(t)表示:
(19)
刀齿运动轨迹矩阵Hi(t)的第n行表示nΔt时刻该刀齿前刀面齿廓曲线的位置坐标。
2 切屑形状特征提取及滚削力模型
2.1 基于切屑几何特性的多齿滚削力模型
本文采用当前金属切削机理研究中应用最广泛的直角正交切削力模型,直角正交切削力模型认为切削力与切屑层的面积正相关:
Fc=KS
(20)
式中,Fc为主切削力,N;K为切屑截面面积为1 mm2时的单位面积切削力,N/mm2;S为切削层面积,mm2。
在滚齿加工过程中,滚刀轴向有多刀齿同时参与切削,工件轴向有相邻刀齿参与切削。某一时刻的主滚削力Fc(t)等于该时刻所有切屑层线性叠加面积与K的乘积:
(21)
式中,Si(t)表示在t时刻i号刀齿展成的切屑切削层面积。
2.2 C#调用动态链接库混合编程
为掌握滚齿加工切屑的形成规律,得到切屑层面积,需根据滚齿加工各坐标轴运动关系进行三维运动仿真,提取切屑的几何特征,以形成切屑三维实体模型。为此,将MATLAB的计算功能与SolidWorks的三维建模功能结合,通过C#编程实现刀具与工件实体间的布尔运算,从而得到切屑三维实体。
滚齿加工三维运动仿真流程如图6所示,具体步骤如下。
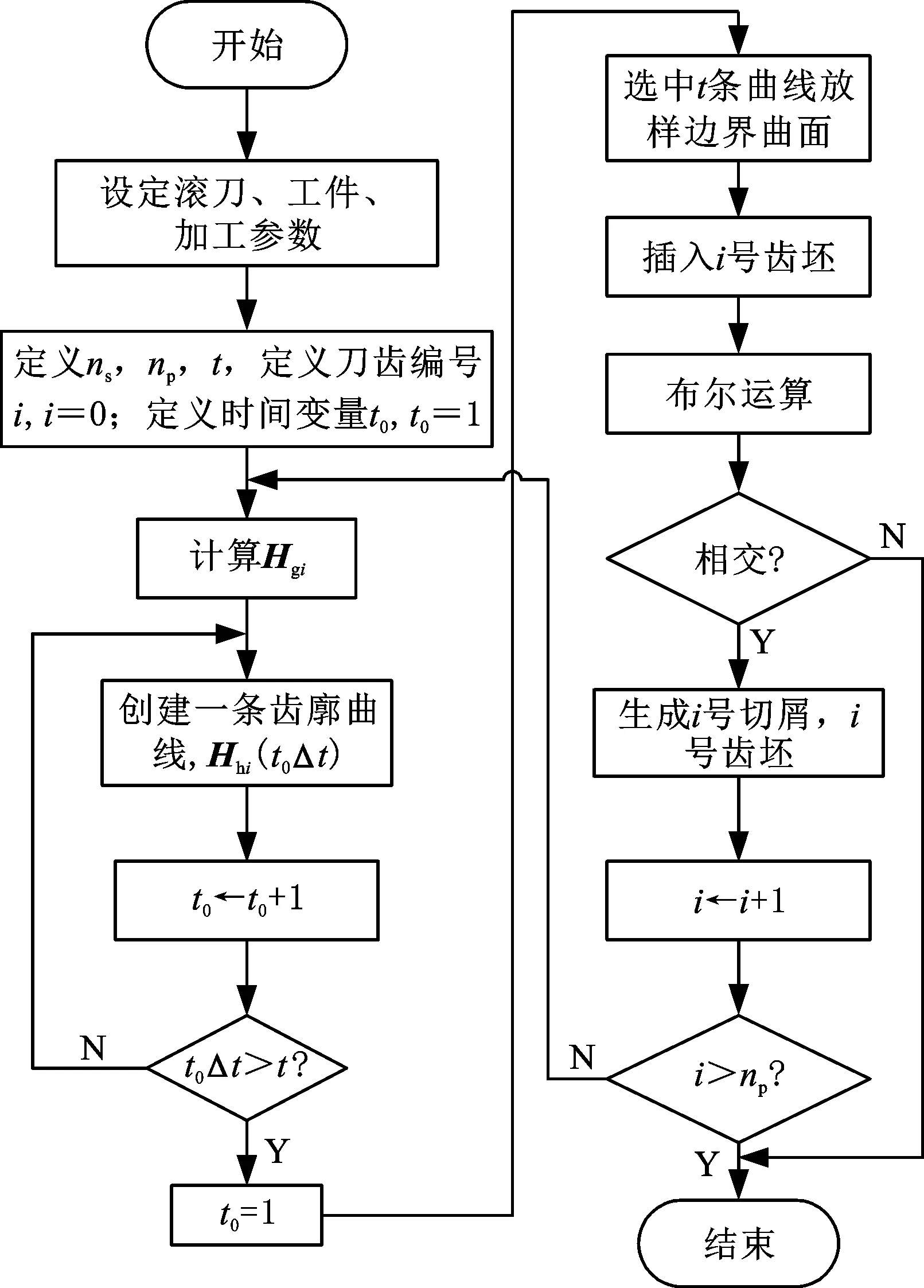
图6 三维运动仿真流程图Fig.6 3-D motion simulation process
(1)设定滚刀参数、工件参数和加工参数,编写刀齿齿廓曲线、刀齿运动轨迹的MATLAB程序,将计算生成的刀齿运动轨迹点坐标保存。
(2)刀齿运动轨迹点坐标导入SolidWorks中,连接成闭合样条曲线。
(3)如图7所示,将一个刀齿的轨迹样条曲线放样成边界曲面,生成的刀齿运动轨迹曲面与待加工工件三维实体模型进行三维布尔运算。一方面,布尔差运算生成的三维实体为本次切削形成的齿坯,该齿坯作为待加工工件参与下一刀齿的切削过程;另一方面,布尔交运算生成的三维实体为本次切削去除的未变形切屑。

图7 切屑、齿槽获取流程图Fig.7 Chip and groove acquisition process
(4)仿真加工完成时,待加工工件上已形成了完整的齿槽,未变形切屑组成的集合为该工件被切除的实体。
在MATLAB中编写刀齿运动轨迹M文件(包括空间坐标变换、空间曲线离散等关系运算和数据处理),使用自带的deploytool工具箱打包封装为动态链接库(dll文件);在SolidWorks中,批量读取刀齿轨迹坐标点,生成封闭曲线、边界曲面,实现三维布尔运算,并录制宏程序,生成相应动态链接库;C#除了调用MALTAB和SolidWorks生成的动态链接库以外,还用于实现设置加工参数、保存文件路径等功能。混合编程关系如图8所示。

图8 混合编程关系图Fig.8 C# mixed programming diagram
在SolidWorks中编写宏程序时,使用的方法和功能包括InsertProtrusionBlend(放样凸台)、InsertMoveCopyBody2(平移和复制)以及InsertCombineFeature(布尔运算)等。
2.3 切屑几何特性提取
本文提出等角分割法提取切屑特征。在计算刀齿运动轨迹时,以等时间间隔计算刀齿齿廓曲线在工件坐标系下的轨迹,滚刀转速不变,在相同时间间隔内滚刀转过的角度不变。如图9所示,以组成刀齿轨迹曲面的齿廓曲线所在的平面作为参考平面能等角度分割切屑。

图9 等角分割法Fig.9 Equal-angle segmentation
滚齿加工过程中存在相邻刀齿同时参与切削的现象,在计算切削力的时候,需同时提取相邻刀齿切除切屑的几何特征。等角分割法提取的切屑几何特征能准确地描述时域上切屑形成的过程。第i号刀齿和第i+1号刀齿同时参与切削,等角分割法能方便准确提取同时切削的切屑层面积。
3 仿真与试验
3.1 仿真与试验参数
为了验证建立的多齿滚削力模型的有效性,利用秦川机床工具集团生产的搭载华中9型数控系统的YK3126数控滚齿机进行加工试验,加工参数如表2所示。

表2 加工参数Tab.2 Machining parameters
图10所示为通过加工仿真得到的未变形切屑、齿槽的三维实体和实际现场加工的变形切屑、齿槽。仿真加工的切屑与实际加工的切屑形状相似。沿齿形方向上,由于滚刀上存在容屑槽,滚刀通过有限刀齿进行断续包络,形成的实际齿形是多条线段构成的近似曲线,而不是光滑的渐开线,沿齿向上,对于某个齿槽,滚刀以恒定的走刀速度在齿向的不同位置进行切削,前后两次切削之间存在残留高度,形成的实际齿向不是一条直线,而是波浪线,因此仿真齿槽与实际加工齿槽的表面均会出现明显的“波纹”。

(a) 仿真加工 (b) 端面齿形 (c) 轴向齿形

(d) 仿真切屑 (e) 仿真齿槽

(f) 实际切屑 (g) 实际齿槽图10 仿真加工与实际加工的切屑、齿槽对比Fig.10 Chip and groove comparison between simulation and machining
仿真加工表面的“波纹”高度如图11所示,加工表面误差为±0.035 mm。在模拟仿真加工过程中,CAD软件进行大量布尔运算,受运算精度限制,模拟仿真加工存在一定误差;另外对滚刀齿形进行离散化处理和对离散的切削轨迹进行边界放样也存在一定误差。

图11 仿真加工齿槽表面波纹高度Fig.11 Surface corrugation height of simulation groove
切削面积随刀齿转角变化如图12a所示,18号切屑在刀齿转角为15.9°时切削层面积最大,为0.357 mm2。以滚刀旋转360°为一个周期,加工形成切屑的瞬时切削面积随滚刀转角变化如图12b所示,18号切屑在滚刀转角为79.5°时切削层面积最大,为0.357 mm2。

(a) 切削面积随刀齿转角变化

(b) 切削面积随滚刀转角变化图12 切屑面积变化Fig.12 Chip area change
3.2 瞬时滚削力试验
HNC-SSTT是华中数控系统配套的在线检测、离线分析工具。HNC-SSTT在线采集过程如图13所示,安装了HNC-SSTT的PC机通过网线与华中9型数控系统相连,数控系统将加工过程中机床各轴的负载电流数据通过多通道采集卡传输给PC机,负载电流的时域波形图在HNC-SSTT客户端上实时显示。试验参数如下:B轴电机额定电压380 V,采样频率9600 Hz。加工参数如表2所示。

图13 HNC-SSTT在线采集过程Fig.13 HNC-SSTT online acquisition process
设B轴瞬时负载电流为I,电机额定电压为U,滚刀的线速度为vB,滚刀外径为d。B轴的负载功率P由切削功率Pc、空载功率Ps和待机功率Pu组成,在转速一定时,待机功率与空载功率几乎为定值[15],瞬时滚削力能通过下式换算:
P=UI=Pc+Ps+Pu
(22)
Pc=FcvB
(23)
(24)
(25)
仿真加工的单位面积切削力系数选自正交切削数据库,K=2030 N/mm2。以滚刀旋转一周为一个切削周期,仿真加工的瞬时滚削力与实测瞬时滚削力对比结果如图14所示。
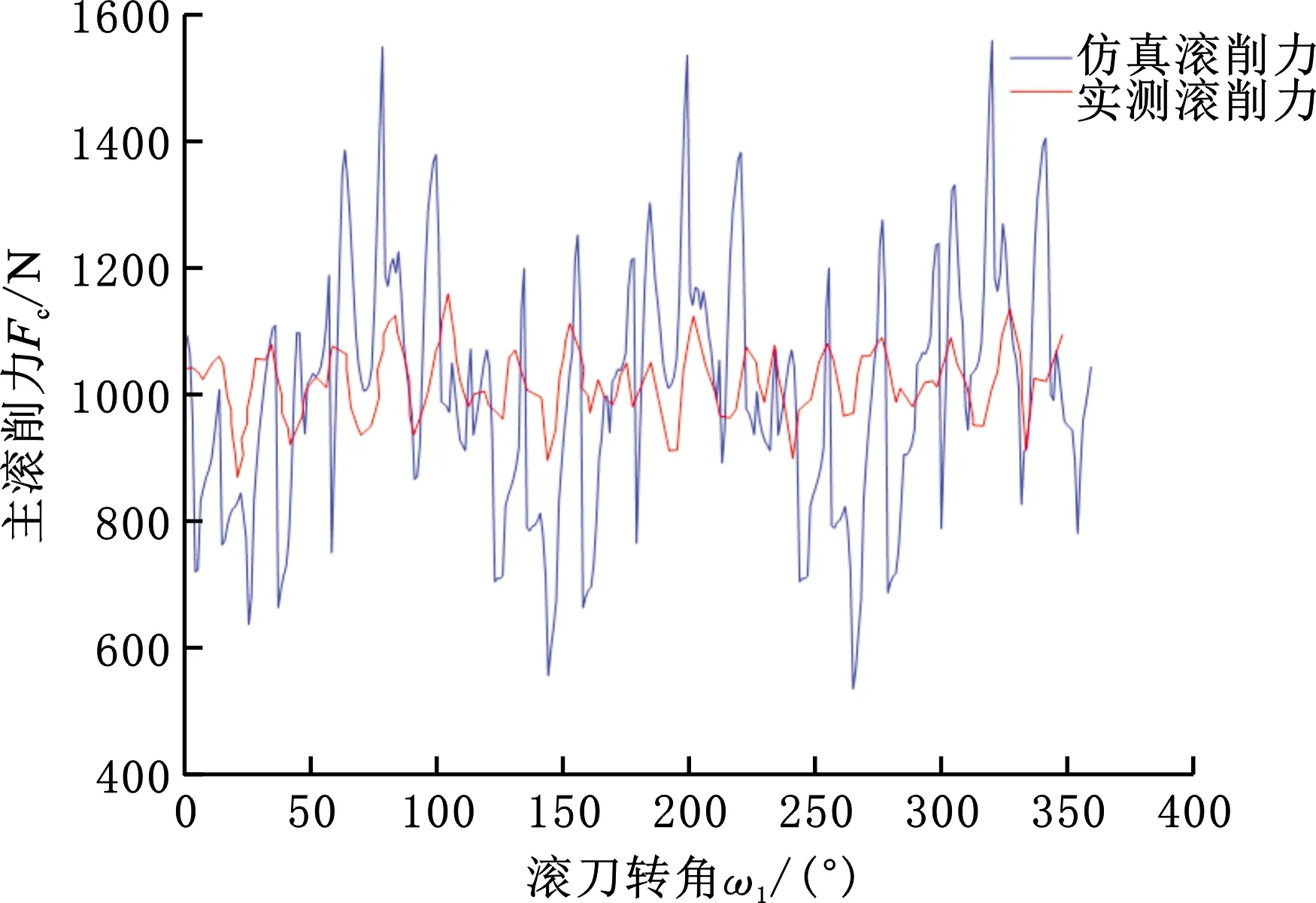
图14 滚削力对比Fig.14 Hobbing force comparison
在滚刀转角25°、150°和265°等处附近仿真滚削力和实测滚削力都处于波谷;在135°、205°和280°等处附近仿真滚削力和实测滚削力都处于波峰。从相位上看,仿真滚削力和实测滚削力变化趋势基本吻合。同时实测滚削力和仿真滚削力的平均值大致相等,但在幅值上存在一定差异。主要原因是未考虑切削过程中切屑流动干涉和单位面积切削力系数动态变化等因素;另外滚刀转速快,采样频率较低,丢失了一些数据。
总体而言,仿真滚削力与实测滚削力变化趋势较吻合,证明了仿真滚削力在实际加工中具有一定的参考意义。
3.3 工艺参数对瞬时滚削力的影响
分别改变滚刀容屑槽数、走刀速度和滚刀头数,仿真瞬时滚削力如图15~图17所示。由图可知:

(a) 容屑槽数k=12 (b) 容屑槽数k=14 (c) 容屑槽数k=17图15 改变容屑槽数的瞬时滚削力Fig.15 Instantaneous hobbing force with varying chip grooves

(a) 走刀速度af=1.2 mm/r (b) 走刀速度af=1.5 mm/r (c) 走刀速度af=2.0 mm/r图16 改变走刀速度的瞬时滚削力Fig.16 Instantaneous hobbing force with varying tool walking speed
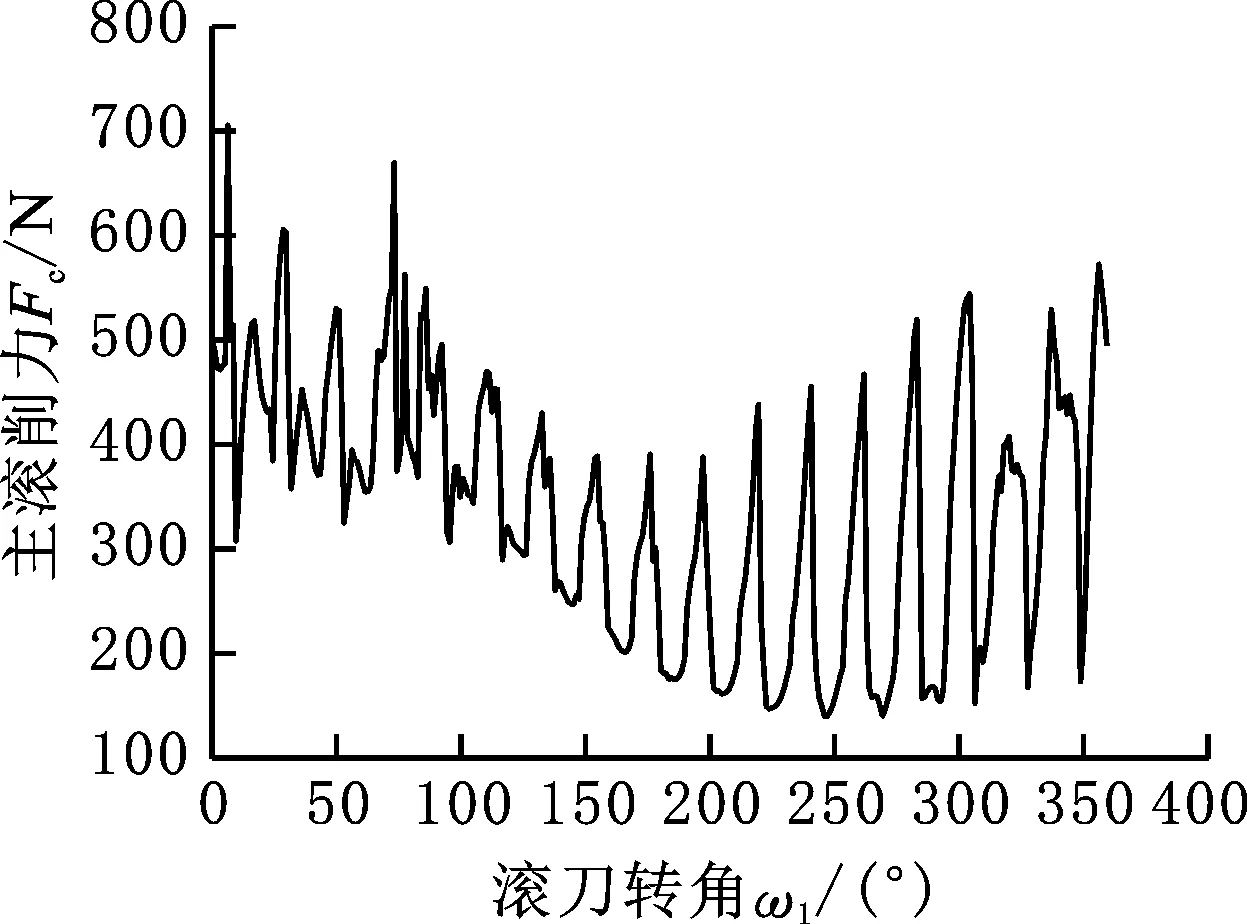
(a) 单头

(b) 三头图17 改变滚刀头数的瞬时滚削力Fig.17 Instantaneous hobbing force with varying number of hob heads
(1)瞬时滚削力是随滚刀旋转角度变化的变应力,由于滚刀上布置容屑槽,一个切削周期内,滚削力的波峰数等于容屑槽数。
(2)改变走刀速度,瞬时滚削力波形图的形状基本不发生变化,但滚削力的幅值改变。
(3)改变滚刀头数计算瞬时滚削力时,不仅要考虑同一螺旋线上多刀齿切削叠加的滚削力,还要考虑不同螺旋线上刀齿叠加的滚削力,因此,滚刀头数改变引起瞬时滚削力波形图的形状和幅值均发生较大变化。
3.4 瞬时滚削力波动特性分析
分别改变滚刀容屑槽数、走刀速度和滚刀头数,一个周期的瞬时滚削力平均值、最大值、最小值、均方差见表3。

表3 加工参数对瞬时滚削力的影响Tab.3 Effect of machining parameters on instantaneous hobbing force N
增加容屑槽数,滚削力的平均值和均方差减小。滚削力波动降低的同时,各刀齿受力更均匀,滚刀磨损降低。
提高走刀速度或增加滚刀头数,滚削力平均值、最大值、最小值和均方差均增大,虽然能提高加工效率,但滚削力波动大,刀齿受力不均匀,负载增大,主轴振动加剧,滚刀磨损加快。
为了减小加工过程中的滚削力波动,在保证加工精度和满足滚刀强度的前提下,应增加容屑槽数,适当降低走刀速度和滚刀头数。
3.5 试验验证
在HNC-948系统上二次开发专机界面,在YK3216数据滚齿机上进行验证,加工现场如图18所示,改进前瞬时滚削力波形图用红线表示,改进后瞬时滚削力波形图用蓝线表示,改进后的瞬时滚削力波动明显减小。

图18 加工现场Fig.18 Processing site
4 结论
(1)本文提出了面向切屑形成过程多齿瞬时滚削力的物理建模方法。基于滚刀-工件相对运动关系建立滚刀前刀面空间运动轨迹几何模型,采用等转角分割模型的方法,得到任意时刻多齿切削的切屑层面积之和,进而建立瞬时滚削力模型。
(2)提出滚齿加工切屑形成全过程运动仿真的实现方法。将滚刀前刀面轮廓离散化,通过MATLAB程序生成滚刀前刀面空间运动轨迹的动态链接库;采用SolidWorks建立工件和前刀面运动轨迹三维实体模型,进行布尔运算,得到加工齿槽和切屑实体;采用C#调用MATLAB和SolidWorks动态链接库混合编程实现滚齿加工切屑形成全过程的三维运动仿真。
(3)研究工艺参数对瞬时滚削力的影响,并分析滚削力波动特性,提出降低滚削力波动的措施,并在YK3126数控滚齿机上进行了验证。研究结果为后续分析机床动态特性和优化工艺参数提供了参考。

