冗余混联式钻铆机床姿态调整轨迹优化

潘国威 陈文亮

南京航空航天大学机电学院，南京，210016

0 引言

相比传统手工钻铆，自动化钻铆装备集制孔、锪窝、铆接和检测等功能于一体，易于保证飞机装配钻铆精度的稳定性，越来越多地被用于飞机制造过程中。常见的自动化钻铆装备有基于工业机器人的钻铆系统和专用自动钻铆机床两种类型。相比基于工业机器人的钻铆系统，专用自动钻铆机床具有刚度高、精度高和工作空间大等特点[1]。专用自动钻铆机床通常包含串联形式的上下加工末端执行器和并联形式的调姿托架[2]，在飞机壁板钻铆过程中，通过并联托架实现壁板姿态调整，而串联结构的上下末端可实现较大范围的壁板钻铆[3]。专用自动钻铆机床可等效为一种由并联机构的动平台上连接串联机构组成且含有冗余自由度的混联机构。冗余自由度一方面提高了装备钻铆任务的适应性，另一方面冗余自由度引起的多种可行钻铆姿态增加了轨迹规划的复杂程度。因此，如何充分利用冗余混联特性优化姿态调整轨迹，成为提高自动钻铆机床加工效率、保障飞机壁板钻铆质量的关键。

运动学模型是实现自动钻铆机床姿态轨迹规划和控制的基础。近年来，以李群和李代数为基础的旋量理论在机构运动学建模领域得到了广泛的应用。旋量理论通过研究空间直线的运动及其引起的末端位姿变化的几何代数描述[4]获得机构运动的描述，它在全局坐标系下描述刚体的运动，无需在每个轴上建立局部坐标系[5]，有利于建立统一的机构运动学模型，同时避免了局部坐标系描述带来的奇异性问题[6]。SUN等[7]针对用于飞机装配壁板调姿的混联机构运动学进行研究，通过旋量方法获得了运动学逆解。阳涵疆等[8]提出了一种基于旋量理论构建混联采摘机器人运动学方程的方法，获得末端执行器的位置正解。由以上文献可知，旋量方法可以有效地建立并求解混联机构的运动学模型，但是涉及含冗余自由度混联机构的运动学建模还不多。

自动钻铆机床的冗余混联特性使其在复杂壁板钻铆装配时存在多种满足钻铆任务姿态调整的构型[9]。关于如何优选多种加工可行姿态构型，国内外学者进行了大量的研究。张鹏翔等[10]利用六轴联动数控机床冗余联动特点优化了加工过程轨迹误差，提高了工件加工质量。ZHU等[11]构建了应用于飞机对接环铆装备的运动学模型，利用测地优化方式获得了钻铆姿态调整策略。曲巍崴等[12]应用冗余机器人的自运动特性，以刚度最优为目标建立了飞机钻铆加工姿态调整模型，改善了钻铆加工性能。上述文献主要通过将工件固定，即固定钻铆末端执行器的姿态，通过调整冗余关节的运动来实现不同的位姿调整。钻铆过程中将壁板零件定位在并联托架上，通过控制并联托架实现壁板零件上待钻铆孔位的姿态调整。针对工件在加工过程中姿态也可调整的复杂情况，徐朋等[13]将冗余铺丝机械手的位形空间看作光滑流形，获得了最优化位置和姿态反解的解耦策略。GAO等[14]采用动态规划方法对含有冗余自由度铺丝机的铺丝轨迹进行优化求解，提高了铺丝效率。

自动钻铆机床姿态调姿轨迹优化是钻铆机床运动学逆解的实际应用，对钻铆效率、精度及能量消耗具有重要影响。本文针对钻铆任务，基于旋量理论获得了解析运动学模型；阐述了钻铆机床加工任务多解原理，并基于此构建了调姿轨迹优化模型，利用动态规划方法对该模型进行求解；最后通过实验验证所提方法的有效性。

1 混联冗余自动钻铆机床

1.1 系统结构

本文研究的混联冗余自动钻铆机床由龙门式串联结构的上下末端执行器和并联形式的调姿托架组成，其中，上下末端串联分支的运动副分别为PPPR(P为移动副，R为转动副)和PPR结构形式，调姿托架机构为PS-PPS-2PPPS(S为球副)的非对称的少自由度并联机构。龙门定位系统可带动上下末端执行器在空间中运动，保证末端执行器钻铆的精确定位，调姿托架用于实现壁板姿态的精确调整，如图1所示。

图1 混联冗余自动钻铆机床Fig.1 The redundant and hybrid ADRM

1.2 冗余特性分析

待钻铆壁板的几何特性及钻铆工艺需要混联结构形式的自动钻铆机床实现5个自由度(x，y，z，α，β)的姿态调整能力。根据自动钻铆机构的结构形式，上末端的自由度M1=4，即(X1，Y1，Z1，A1)；下末端的自由度M2=3，即(X2，Y2，A2)；并联调姿托架具有绕A3轴、B3轴转动和沿Z3向移动3个自由度，即(A3，B3，Z3)，如图2所示。由于完成钻铆任务时，钻铆轨迹规划的公共约束为待钻铆点位姿，故上下末端和托架之间共同存在的A轴调整即为自动钻铆机床的冗余自由度，该冗余自由度增加了运动学求解的难度，同时也为姿态调整轨迹优化提供了可能。因此，针对给定的钻铆任务，如何选择合理构型成为钻铆机床姿态调整轨迹规划的重点和难点，也是决定钻铆效率和质量的关键。

图2 自动钻铆机床自由度结构关系Fig.2 DOF relationship of the ADRM

1.3 钻铆机床运动学模型

在钻铆过程中，为了满足钻铆点的法向姿态在上下末端的A轴转动平面内，首先需要通过调整并联托架B轴将待钻铆孔位法矢旋转至A轴转动平面内，然后通过同步调整并联托架各驱动轴，实现托架平台在A轴和Z向的自由运动。因此，为了便于运用旋量方法统一构建自动钻铆机运动学模型，在建立运动学模型时将并联托架等效为仅有A轴和Z向两个运动自由度的串联机构。建立图3所示的坐标系，ObXbYbZb为基坐标系，简记为{Ob}；OwXwYwZw为建立在调姿托架上的工件坐标系，简记为{Ow}；Ot1Xt1Yt1Zt1和Ot2Xt2Yt2Zt2分别为建立在上下末端的坐标系，分别简记为{Ot1}和{Ot2}。从基坐标系到上下末端和托架分别形成上末端运动链、下末端运动链和工件链，分别建立上末端-下末端链和下末端-工件链。根据旋量理论[15]，基坐标到上下末端和工件坐标系间的位姿变换为

(1)

(2)

(3)

图3 自动钻铆机床运动学结构Fig.3 Kinematic chains of the ADRM

1.4 钻铆机床逆运动学求解策略

运动学逆解是运动控制和轨迹规划的基础。根据式(1)～式(3)所示的自动钻铆机床运动学关系可以推导出运动学逆解，但冗余自由度的存在增加了解析求解的难度。为了降低求解难度，首先通过建立式(2)和式(3)所示的下末端-工件链模型，求解下末端和调姿托架的运动学逆解。在此基础上，通过上下末端的几何协调关系，获得上末端的运动学逆解[16]，获得的反解为

(4)

式中，nx、ny、nz为目标位置的法向分量；θA3、θA2分别为托架和下末端的A轴旋转量；l12为托架z1和z2之间的距离；下末端转轴上点PA2坐标记为(xA2，yA2，zA2)；θA1为上末端的A轴旋转量；lT1和lT2为上下末端端点到对应转动轴间的偏距；上末端转轴上点PA1坐标记为(xA1，yA1，zA1)。

综上，利用旋量方法建立的自动钻铆机床运动学模型仅需知道钻铆机床各轴在{Ob}中的基本几何信息和各轴的运动信息，便可通过运动学模型直接获得末端执行器相对于壁板零件的钻铆姿态，无需对具体的自动钻铆机结构建立局部坐标系及其对应的矩阵变化关系，简化了建模过程。

2 钻铆任务描述

从飞机钻铆离线编程软件中可以获得各钻铆点的位置和法矢信息，即pi=(xi，yi，zi，ai，bi，ci)T，在每个钻铆点建立局部坐标系WiXiYiZi，其中Zi为钻铆点法矢方向，定义Xi方向为当前钻铆点和下一个钻铆点的连线方向，即Xi=pi+1-pi，Yi方向由右手定律确定。根据每个钻铆点的坐标定义方法，Twi为每个钻铆点到{Ow}的齐次变换矩阵，钻铆任务可写成一系列齐次变换：

Tw1→Tw2→…→Twn

(5)

根据式(5)给定的钻铆任务，冗余自由度的存在使得完成每个钻铆点都存在无穷多个可行姿态，如图4所示。

图4 钻铆构型多解示意图Fig.4 Infinite variety of configurations for each fastening point

3 钻铆姿态调整轨迹动态规划求解

为了最大化应用自动钻铆机的冗余特性，钻铆姿态轨迹规划的过程如下：①建立钻铆机床和待钻铆零件三维模型，并对待钻铆孔位加工信息进行提取和分类；②考虑钻铆机床运行平稳性、运动范围和碰撞等约束条件，在笛卡儿空间中进行钻铆轨迹规划；③通过运动学映射关系规划关节空间运动；④通过后置处理完成钻铆程序的输出，进行钻铆作业[17]，如图5所示。

图5 钻铆姿态轨迹规划过程Fig.5 The trajectory planning utilizing the redundancy

3.1 笛卡儿空间姿态调整动态规划

为了便于在整个钻铆过程中发挥各轴特性，选择上下末端和托架的协作工作空间中心安装定位壁板工件，并选定钻铆开始点和结束点。根据冗余特性，将每个钻铆点的可行连续解离散化，每个中间点都有多种可行解，将钻铆点A轴转动范围按步长δh离散成m组加工姿态，根据离散化结果，将姿态调整轨迹表示为多层全连接结构形式，计算最短姿态调整路径，如图6所示，则钻铆任务即式(5)的姿态调整最优钻铆点序列为

Wk1，1→Wk2，2→…→Wkn，n

(6)

图6 可行解空间离散化和全连接层模型Fig.6 Discretized nodes and the multi-layer connected structure

其中，Wki，i为第Wi个待钻铆孔位的离散空间中的ki位置。为了充分利用自动钻铆机床冗余特性来调整加工姿态，以钻铆过程中各运动轴的行程最短即能量消耗最少构建姿态调整优化目标函数：

(7)

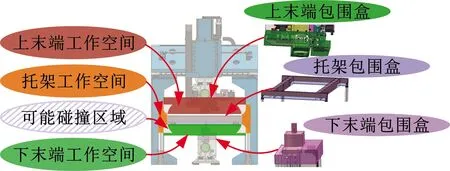
图7 调姿过程碰撞检测模型Fig.7 Collision detection model in the posture adjustment

根据给定的钻铆任务，式(7)的姿态调整能量消耗最小问题可以转化为搜索完成钻铆点间运动各轴的最短路径问题。最短路径问题可以通过常规的A*和Dijkstra等算法求解，但是该类方法在求解壁板零件上有大量待钻铆孔位时计算效率较低。另外，增加钻铆点时需要对全局进行重新优化计算，对钻铆任务的柔性适应能力不足。动态规划算法[14]通过将待求解的问题分解归纳为更小的、相似的子问题，且原问题的最优解中包含了子问题的最优解，最终通过求解子问题产生一个全局最优解[18]。钻铆过程的顺序性使得式(7)可以采用动态规划算法对轨迹姿态进行优化求解。定义tki，i为当前钻铆点Wki，i与起始钻铆点Wk，1间的最短姿态调整时间，则下一个钻铆点Wki+1，i+1与起始钻铆点间的最短姿态调整时间为

tk，i+1=min(W(k，i)+t(W(ki，i)，W(ki+1，i+1)))

(8)

式(8)称为钻铆姿态调整动态规划状态转移方程。采用动态规划中自顶向下的递归算法，通过结合式(6)～式(8)求解式(5)，获得笛卡儿空间完成钻铆任务姿态调整的能量消耗最小轨迹。

3.2 关节空间轨迹光顺

由于钻铆任务的特殊性，各钻铆点之间的运动可以看作点到点的轨迹调整运动。通过获得的笛卡儿空间最优轨迹确定各钻铆点在全局坐标系下的坐标，以这些钻铆点位姿为边界条件，基于5次多项式对自动钻铆机进行关节空间轨迹光顺[19]：

(9)

式中，tb、tf分别为初始时间和终止时间；qb、qf分别为初始和终止位姿时自动钻铆机各主动关节所对应的位置。

4 实验验证

在冗余混联式自动钻铆机床上进行钻铆实验验证。调姿托架z1到z2距离l12=4420 mm；z2到z3距离l23=1400 mm；上末端执行器刀具点与其转动副间的偏距lT1=478.5 mm；下末端顶铆点与其转动副间的偏距lT2=567 mm。

某无人机复材壁板上点1～5为待钻铆孔位，在坐标系{Ob}下的坐标分别为：(250 mm，482.963 mm，129.411 mm，0，0.966，0.259)，(250 mm，304.381 mm，396.677 mm，0，0.609，0.793)，(250 mm，0，500 mm，0，0，1)，(250 mm，-304.381 mm，396.677 mm，0，-0.609，0.793)，(250 mm，-482.963 mm，129.411 mm，0，-0.966，0.259)，其中，R、Q、N和D点为装配夹持固定点，如图8所示。由前文可知，在孔1～5

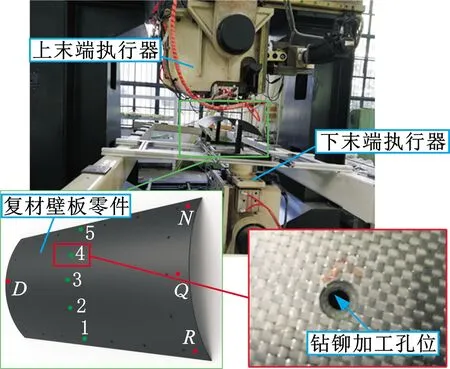
图8 实验方案Fig.8 Experiment platform

钻铆过程中，自动钻铆机床存在不同的姿态调整轨迹。为了对比本文所提方法的有效性，首先将调整托架固定，此时1～5孔位点仅存在唯一的制孔姿态，通过设定各轴的运动速度，计算完成1～5钻铆孔姿态的调整时间为79.2 s。然后，采用考虑自动钻铆机床的冗余特性，设1～5孔位可行解范围为±5°，每个孔位选择m=10进行离散化，即增量为1°，利用动态规划方法计算能量消耗最小时的调整时间为59.8 s，姿态调整效率提高24.58%。此时对应的各轴的运动位置见表1。根据所获得的1～5钻铆点时各轴的运动位置，将其作为关节空间轨迹光顺的点到点边界约束，利用多项式方法获得各驱动轴的运动轨迹。将计算结果代入自动钻铆机控制系统中，并实时采集各轴运动数据，根据数据拟合结果获得钻铆时最优调姿轨迹的各移动轴运动速度曲线对比结果，如图9所示。由图9可以看出，各轴运动平稳，理论计算和实际获得的移动轴速度误差小于2 mm/s、转动轴速度误差小于0.05°/s，且未超出各轴限定范围，验证了该算法的有效性。

表1 钻铆点对应各轴运动位置量Tab.1 The motion of each joints of the ADRM

(a) Z1轴速度及误差曲线

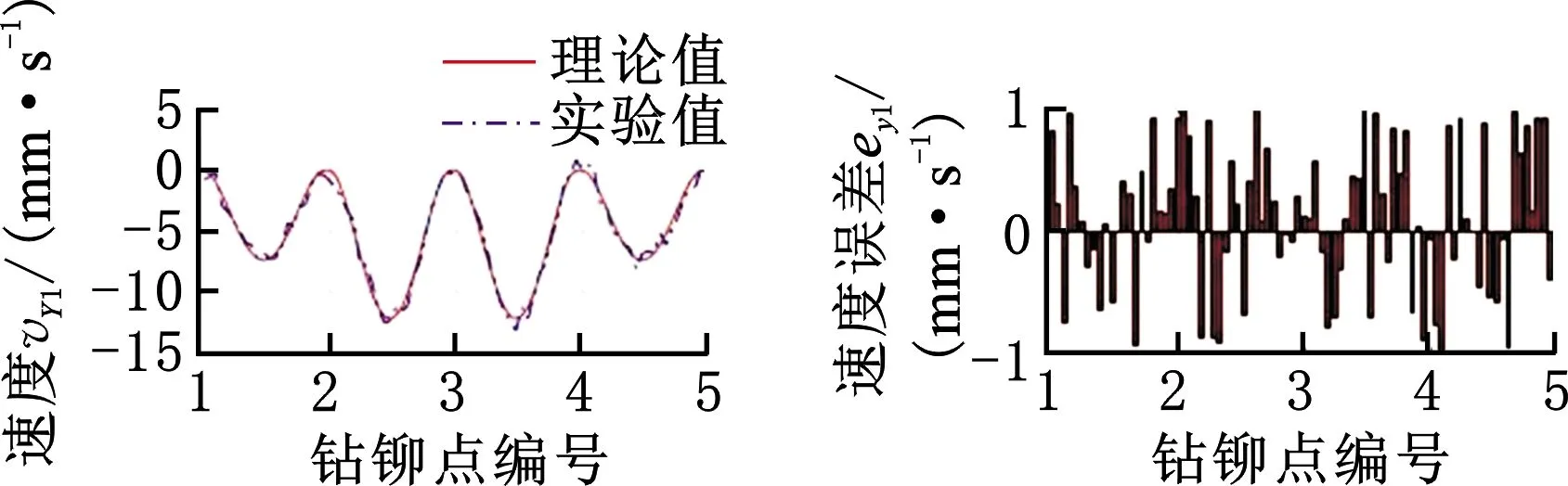
(b) Y1轴速度及误差曲线

(c) A1轴速度及误差曲线图9 关节速度理论值和实验值对比Fig.9 Joints velocity between theoretical and experimental

5 结论

(1)给出了自动钻铆机床加工时的冗余自由度，通过将并联托架等效为串联机构，利用旋量方法建立了混联钻铆机床的统一运动学模型，获得了钻铆机床运动学反解。

(2)针对给定的钻铆任务，阐述了飞机壁板钻铆姿态调整轨迹优化原理；基于动态规划算法获得了完成钻铆任务时的最优姿态调整轨迹，并在关节空间进行运动轨迹光顺，实验结果表明，本文方法可有效提高飞机壁板钻铆效率。