基于改进RRT*FN算法的机械臂多场景运动规划
房立金 吴政翰 王怀震
东北大学机器人科学与工程学院,沈阳,110000
0 引言
随着机械臂的普及,机械臂在复杂环境中的运动规划变得尤为重要。机械臂运动规划的主要目的是在连续空间中寻找一条机械臂末端从起始位置移动到目标位置的无碰撞路径。目前,机械臂通常采用基于采样的规划方法进行运动规划。应用最广泛的基于采样的运动规划算法是概率路线图(probabilistic roadmap method, PRM)和快速扩展随机树(rapidly-exploring random trees, RRT)[1]。
与PRM算法相比,RRT算法更适用于解决高维空间中运动规划问题,因此RRT算法在机械臂的运动规划领域应用较为广泛[2-3]。RRT算法是在起始位置构建一棵树,通过向随机样本生长树来探索状态空间,当得到一条无碰撞路径并到达目标位置时即停止。然而,由于RRT算法是随机抽样过程,在目标区域中发现一个样本通常需要大量时间。针对这一问题,文献[4]提出了RRT-Connect算法。与RRT相比,RRT-Connect算法用两棵树搜索状态空间,从而提高了搜索效率,特别是当目标位置难以通过单向搜索进行采样时效果更加明显。虽然该算法可以有效解决运动规划问题,但无法提供最优解。这是因为用随机采样探索状态空间输出的是一系列随机样本,没有任何优化树的过程,没有考虑初始状态和其他节点之间的运动最优性[5]。
为了解决上述问题,文献[6]提出渐近最优RRT(RRT*)算法。通过执行局部优化来扩展RRT算法,从而改进全局运动规划问题。在找到规划路径后,RRT*算法将继续探索状态空间,通过不断采样以优化当前规划路径。然而,为了实现渐进优化,RRT*算法需要进行大量的迭代过程,导致搜索效率下降。文献[7]提出Informed RRT*算法,通过将搜索区域限制为状态空间的子集来解决RRT*算法存在的缺陷,相较于传统的RRT*算法,Informed RRT*算法能够更快地返回接近最优解。然而,该方法无法限制树的规模[8]。文献[9]提出RRT*FN算法,该算法限制了树中节点的最大值,并移除节点以在其增量采样过程中添加新节点,虽然避免了树的规模无限增长,但收敛精度较低[10]。机器人运动规划过程中,通常将环境中所有障碍物视为静态。然而,在现实场景中,环境中的障碍物并非总是静止或工作的目标点并非固定不变,在动态环境下,上述运动规划算法不能保证良好的适应性。文献[11]提出RRT*FND算法,该算法改善了对动态环境的适应性,但依然存在搜索狭窄通道能力较差、收敛精度较低的问题。
针对上述问题,本文提出一种改进RRT*FN的机械臂运动规划算法。在迭代过程中,采用带有目标偏向性和椭球子集采样的启发式方法对采样区域进行约束采样,使采样点能够更快地收敛到最优值。在扩展节点时,配置树中总节点数的预设值,并通过加权方法对树中叶子节点进行删减,有效避免树的规模无限增长。采用对节点剪枝与连接的启发式重规划方法,使算法更适应动态环境。最后,通过仿真实验进行了验证。
1 相关工作
1.1 运动规划问题定义
本文采用文献[12]的方法对运动规划问题进行定义。设X为状态空间,与障碍物发生碰撞的空间定义为Xobs⊂X,与障碍物不发生任何碰撞的空间定义为Xfree即自由空间。设起始位置为xstart∈Xfree,目标位置为xgoal∈Xfree。因此,起始位置和目标区域之间的路径将被定义为一个集合{σ(0),σ(1)}⊂Xfree,其中σ(0)=xstart和σ(1)=xgoal。
定义路径成本为c:Xfree→R,R表示非负实数集合。寻找路径成本较低的路径是最优路径规划的目标,定义最低路径成本函数为σ*:
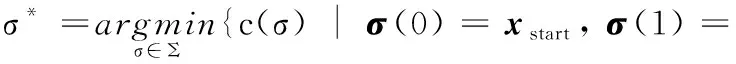
(1)
Xf是状态空间的一个子集,Xf⊆X,它可以提供比现有解决方案更好的方案,设cbest为当前最短路径的成本,则
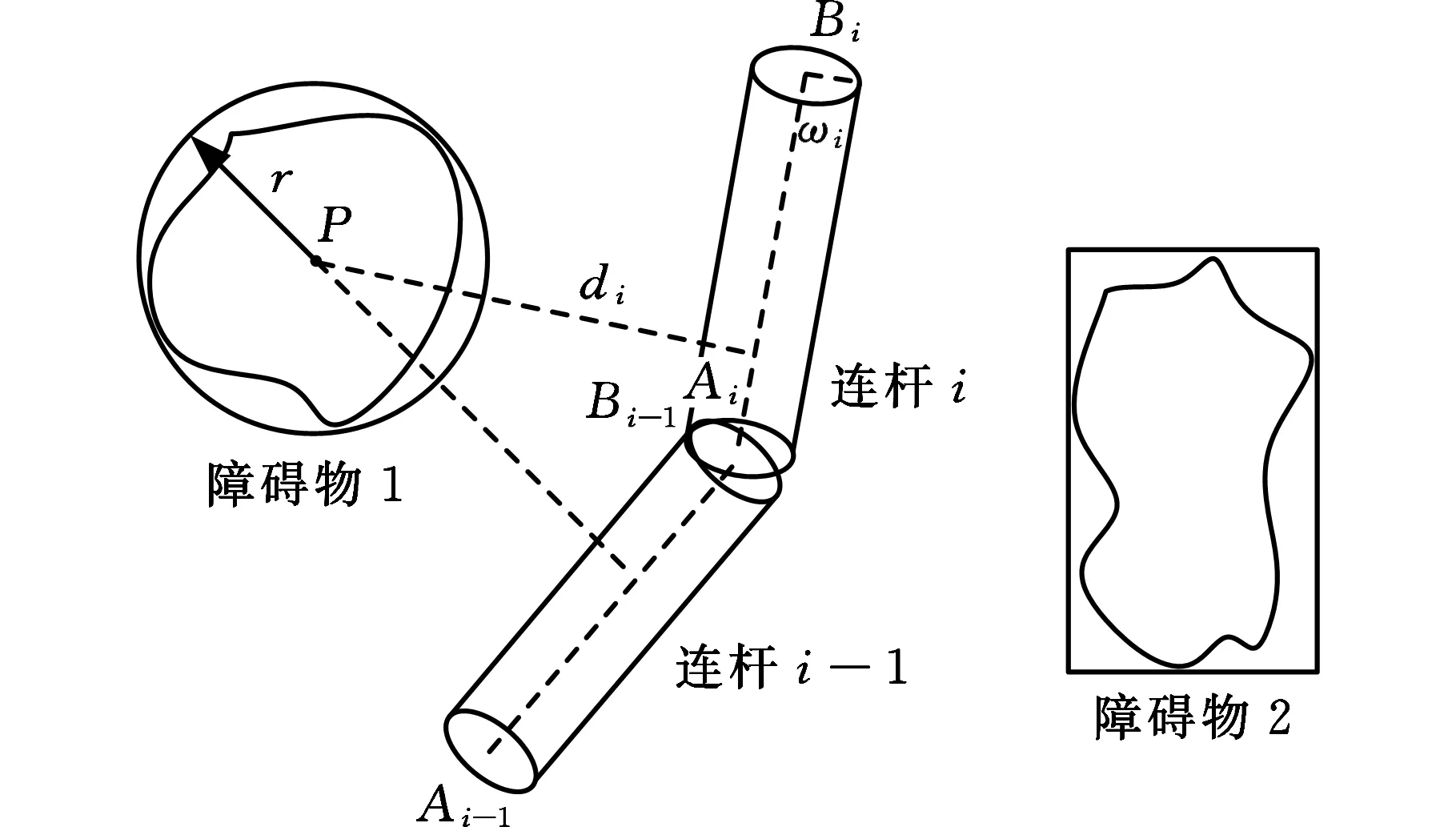
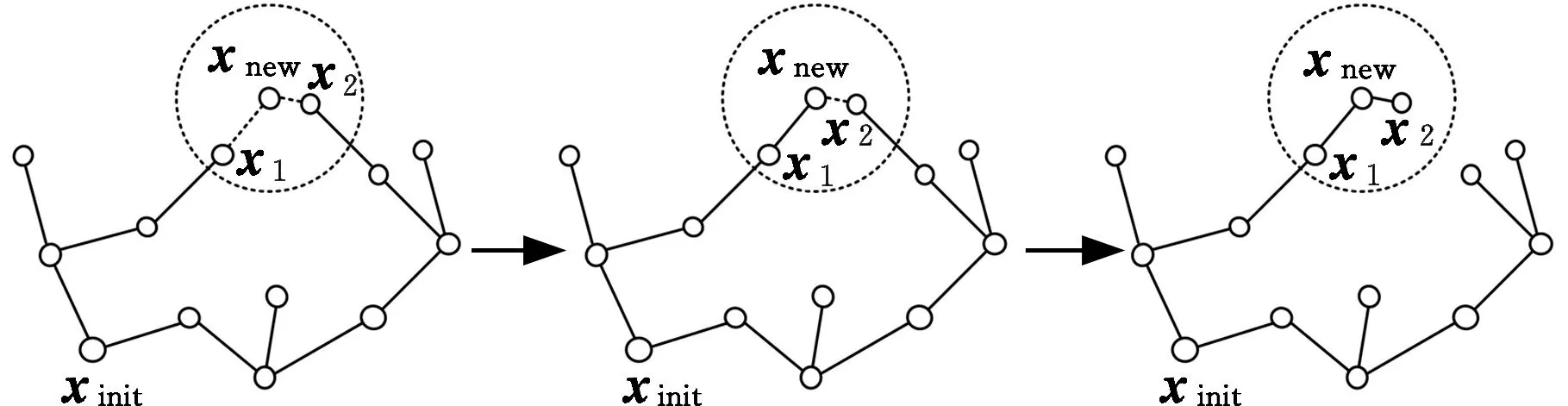
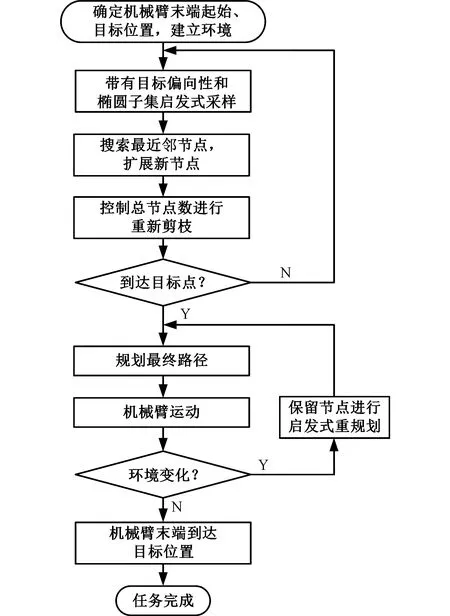
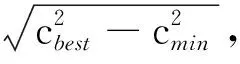
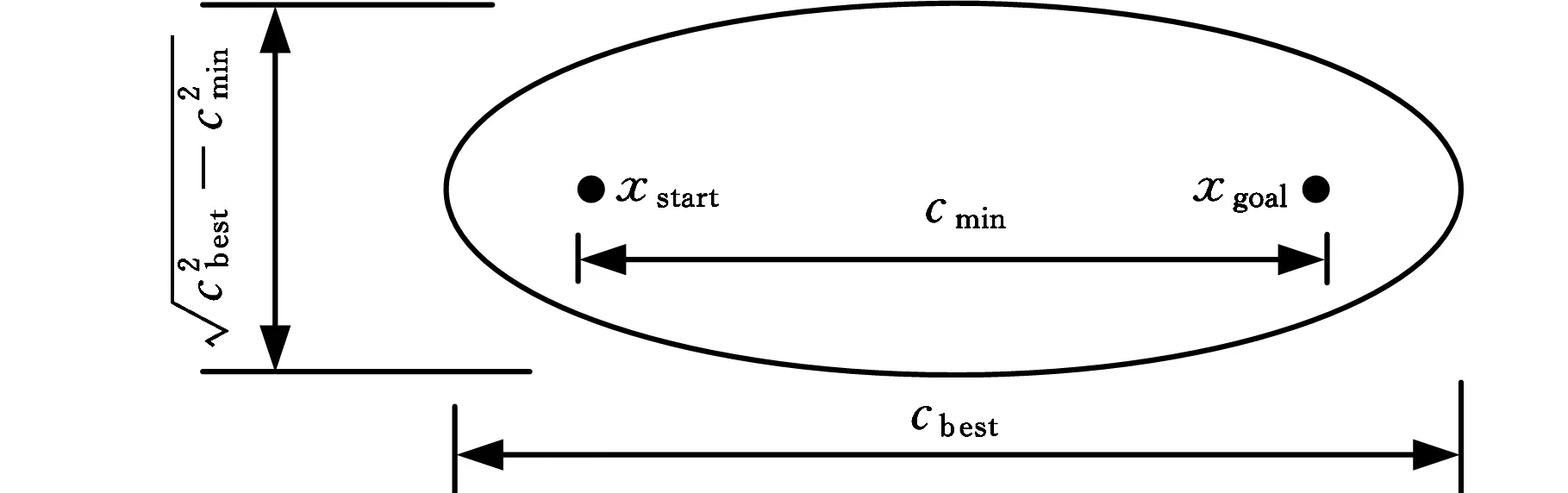
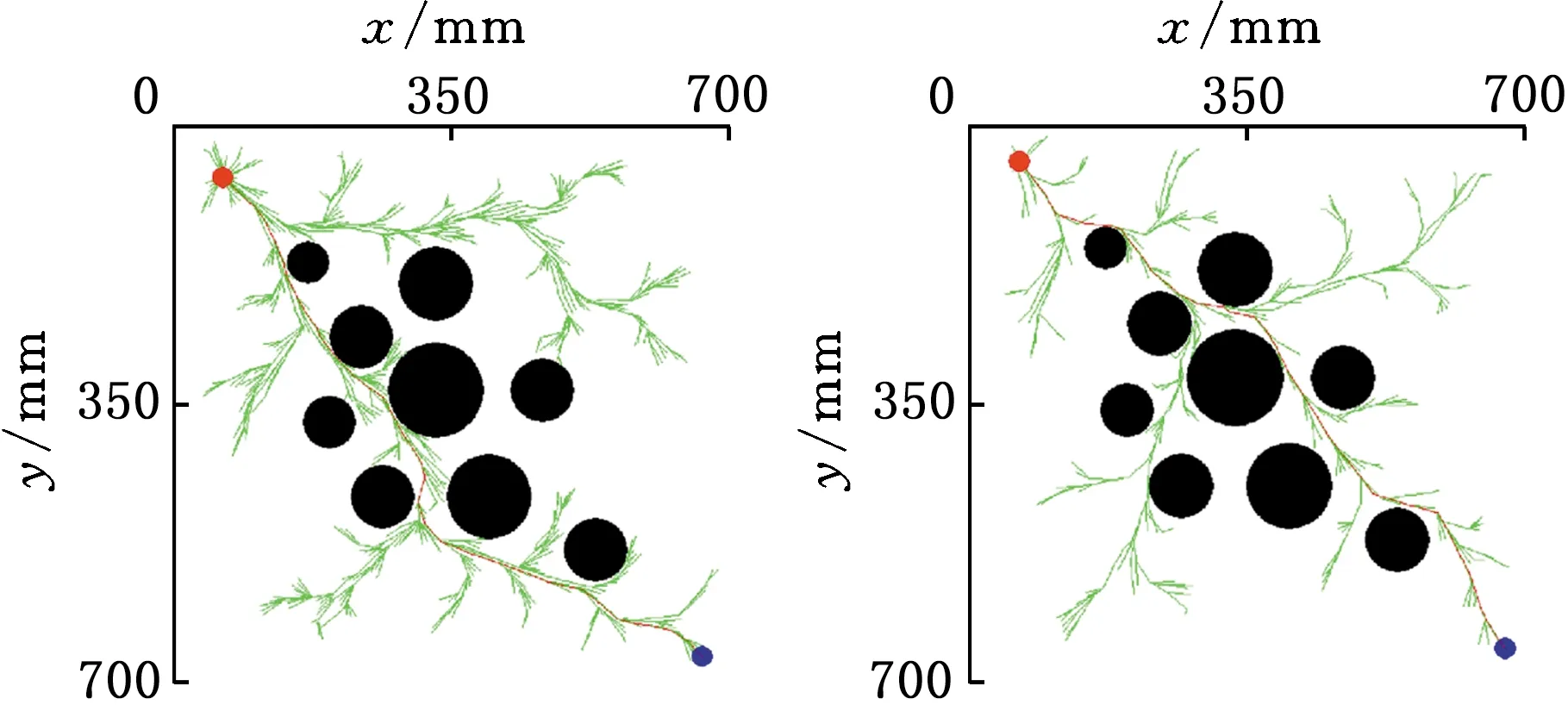
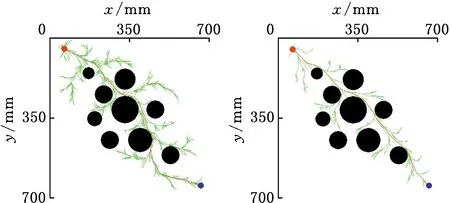
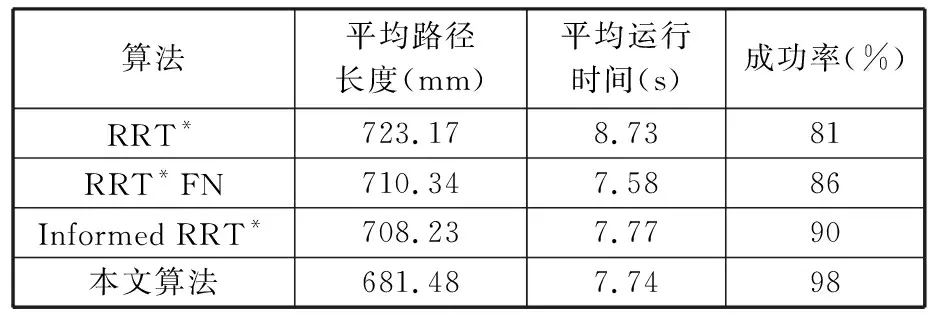
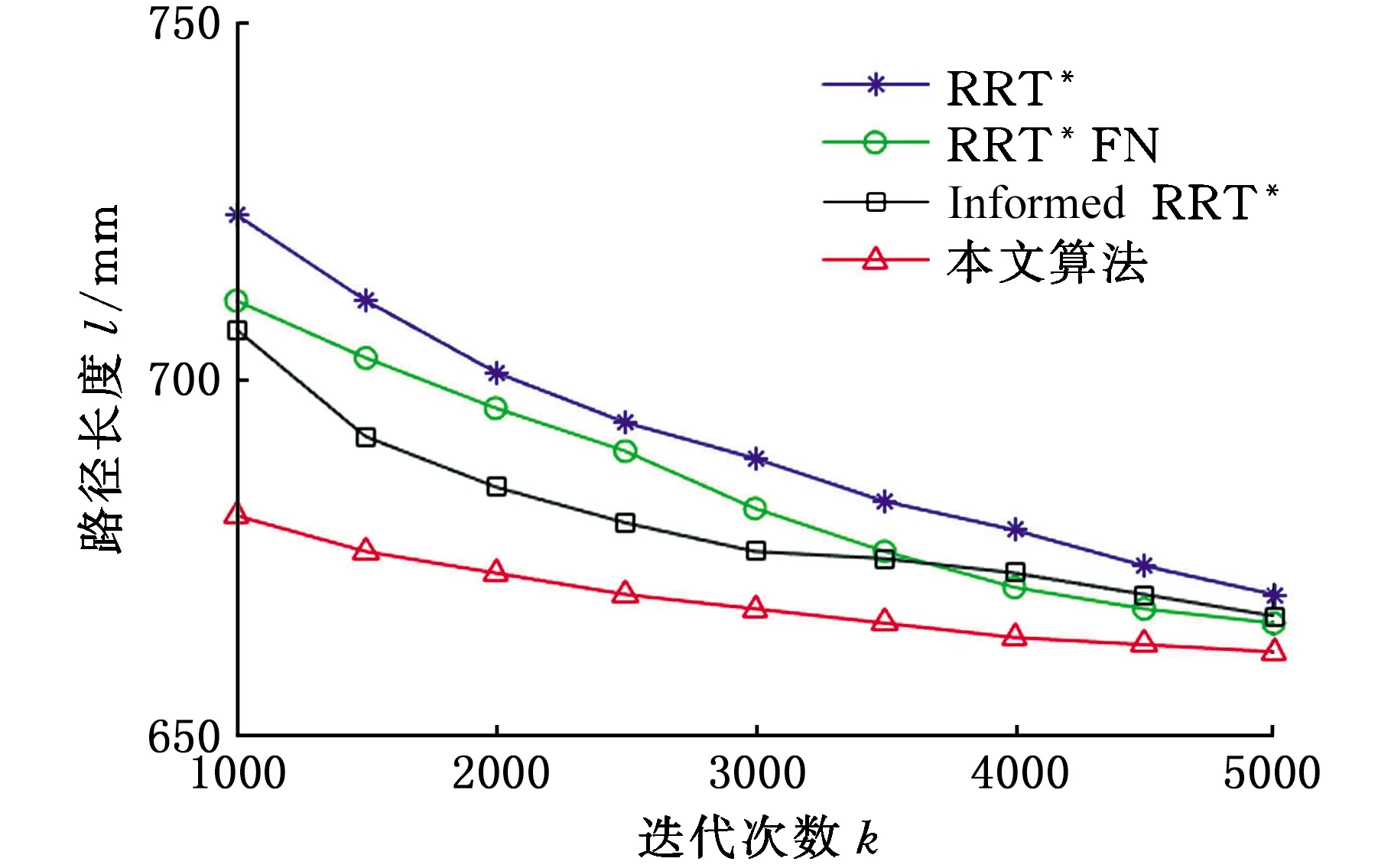
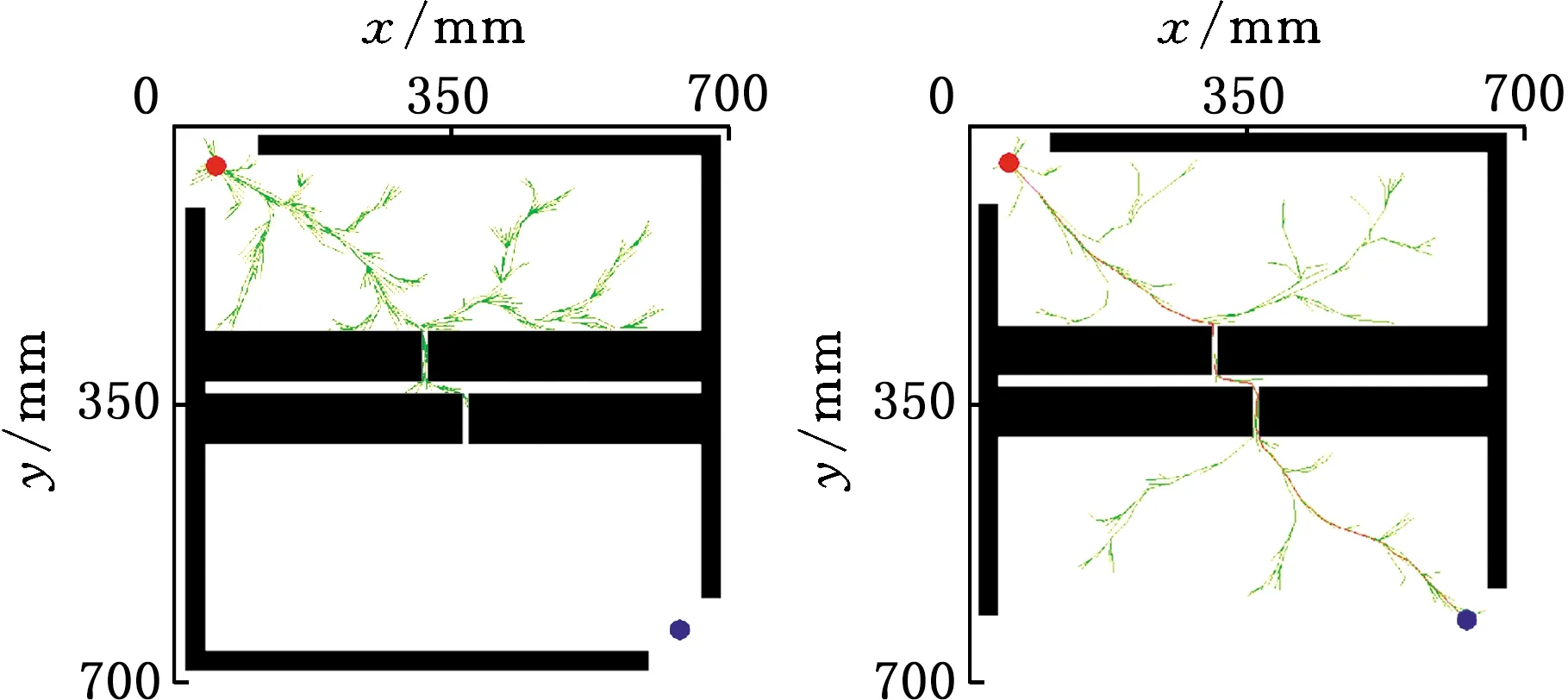
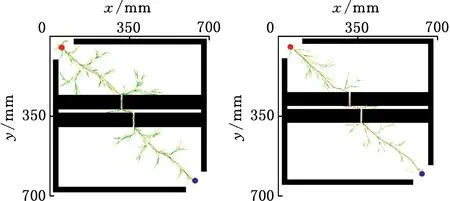
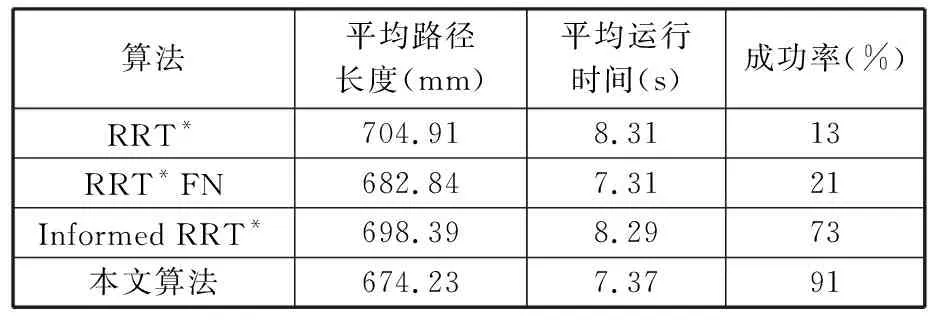
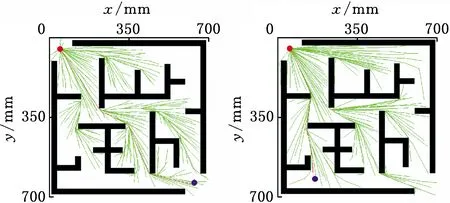
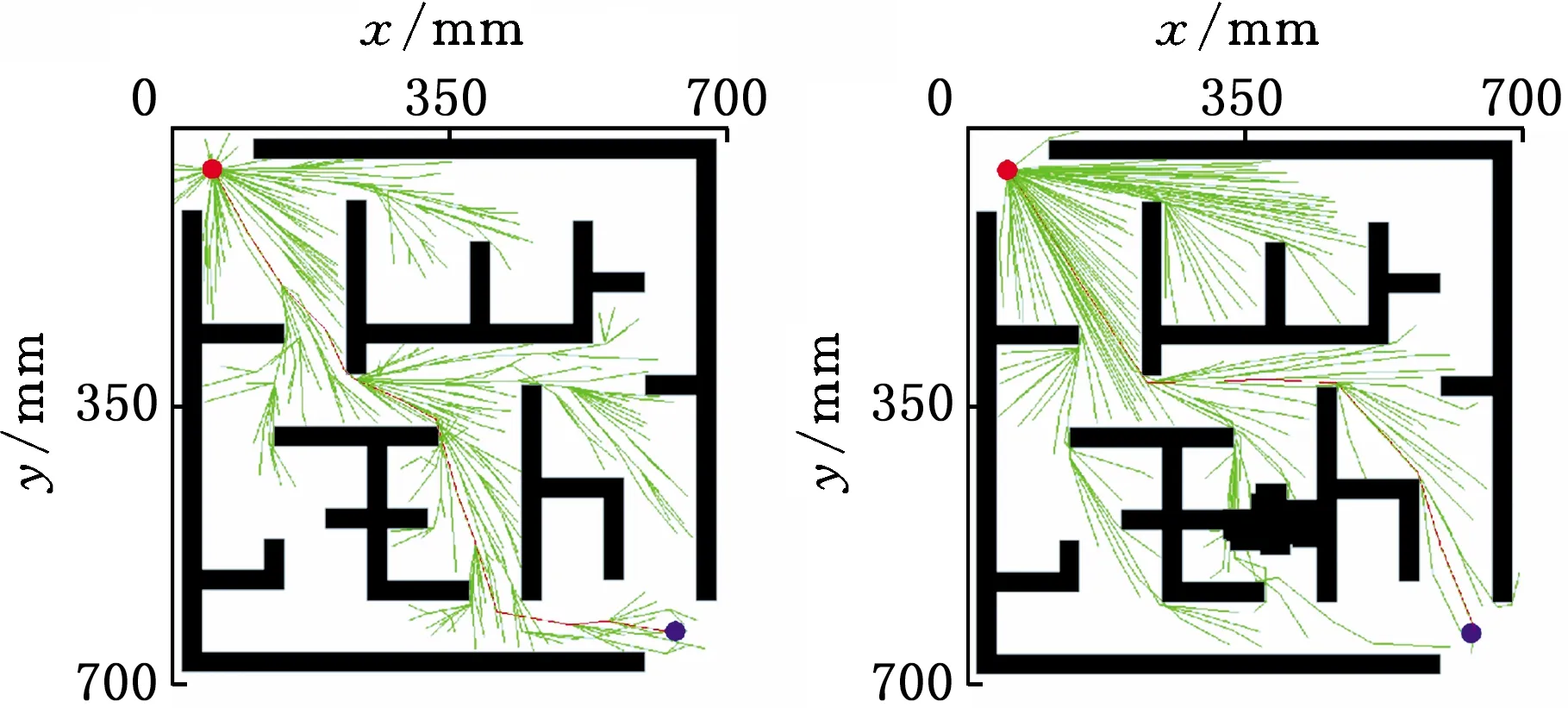
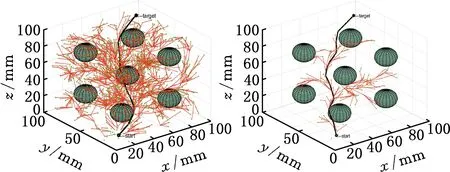
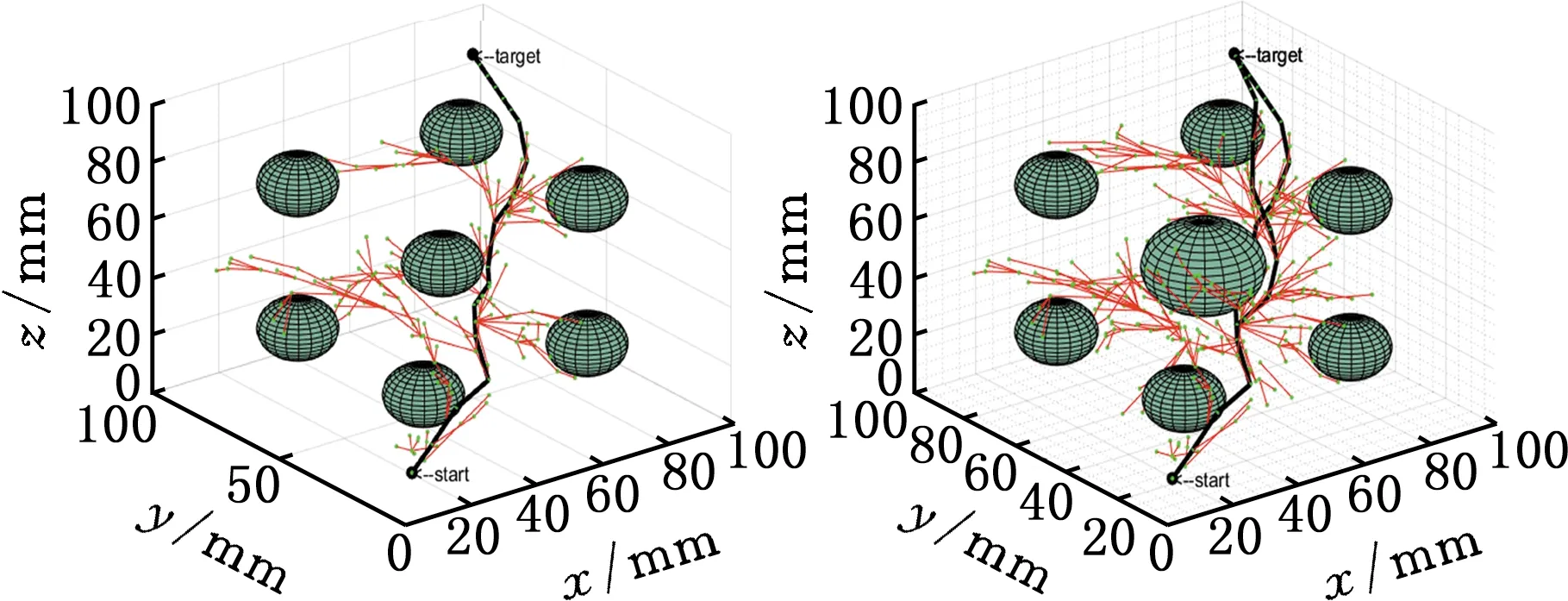
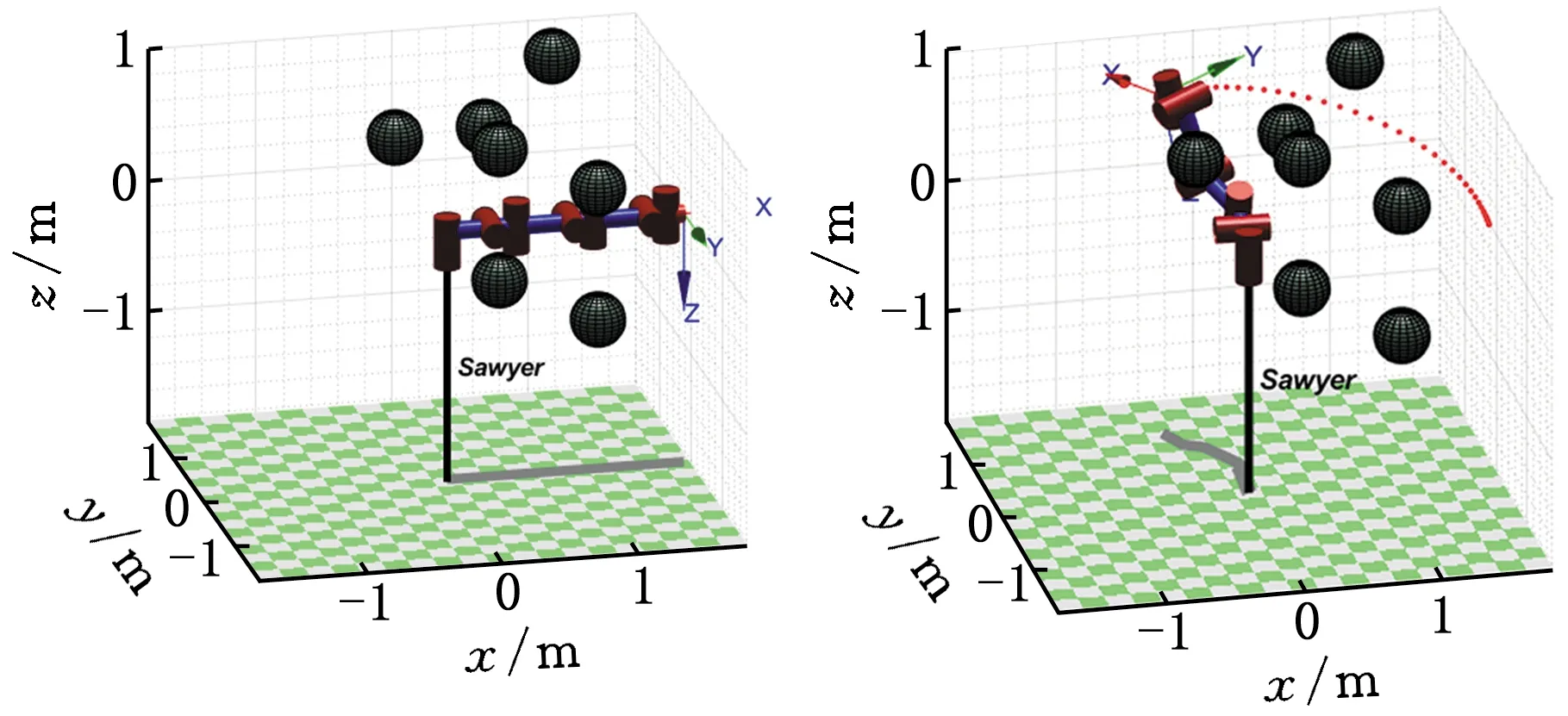
Xf={x∈X∣f(x) (2) 如果规划时将搜索区域限制为Xf,则其状态比整个状态空间少,将可以更快地返回接近最优的解。 机械臂的碰撞检测包括对机械臂末端进行碰撞检测,以及对机械臂各个关节与连杆进行碰撞检测。碰撞检测通常通过空间几何包络法简化障碍物和机械臂模型[13]。在现实环境中,障碍物的形状一般都是不规则的,很难精确建模。本文使用圆柱体描述机械臂连杆,机械臂的碰撞检测问题转换为圆柱体、球体、长方体之间的碰撞检测。 如图1所示,设置球体中心的坐标为(x,y,z)。其中圆柱体是构型空间中机械臂的简化形式,Ai、Bi是连杆i的两端,半径为ωi。针对球形包围盒的碰撞检测,球体是构型空间中障碍物的简化形式,半径为r;球体中心到圆柱体中心轴的距离为di。当di>r+ωi时,机械臂不与障碍物碰撞,反之则发生碰撞。针对轴向包围盒的碰撞检测,若线段AiBi在障碍物的轴向包围盒外,则机械臂不与障碍物发生碰撞,反之则发生碰撞。 图1 碰撞检测模型Fig.1 Collision detection model ADIYATOV等[9]基于RRT*算法[6]提出了一种RRT*FN算法,该算法中采样、扩展节点、选择父节点的方式均与RRT*算法相同。 首先,从无障碍区域随机抽取xrand节点,定位到xrand的最近节点,并将其表示为xnear。然后,通过将xnear的距离扩展到xrand获得新节点xnew,并且找到与xnew的距离小于采样半径r的节点形成集合Xnear。从Xnear中选择节点并进行扩展,从而最小化xnew的累积成本,如图2所示。最后,执行重剪枝程序。重剪枝程序伪代码如下: 1: procedure REWIRE(T,xnear,xnew) 2:for ∀xnear∈Xneardo 3:cnear← COST(xnear) 4:cnew← COST(xnew)+MOTIONCOST(xnew,xnear) 5:ifcnew 6:if COLLISIONFREE(xnew,xnear) then 7:xparent← PARENT(xnear) 8: ifxnearhas no brothers∧M 9: REMOVENODE(xparent) 10:E←E{(xparent,xnear)} 11:E←E∪{(T,xnew,xnear)} 12:returnT 图2 扩展节点示意图Fig.2 Schematic diagram of expansion node 对于Xnear中的每个节点,确定将其父节点设置为xnew是否会降低其累积成本,如果是,则修改节点。RRT*FN算法的重剪枝不同于RRT*算法的重剪枝,因为当树中的节点数大于阈值M时,需要检查每个重新连接的节点的原始父节点是否成为叶节点,如果它成为叶节点,则将其从树中移除。在重剪枝之后,如果树的节点数量T仍然大于M,则随机移除叶节点。 基本的RRT*FN算法是在传统的RRT*算法基础上对树中的最大节点数进行预设,当节点数大于预设值时,树中的叶子节点将被随机删除,使得算法只使用一定内存空间来完成运动规划任务。然而,RRT*FN算法依然存在收敛精度和搜索效率较低的问题。 针对上述RRT*FN算法存在的问题,本文提出了改进的RRT*FN算法。首先,本文对采样方法进行改进,将启发式采样方法加入RRT*FN中,然后采用启发式重规划方法来提高算法对环境的适应性。 改进的RRT*FN算法伪代码如下: 1:V←{xinit};E←∅;T←T∪xinit 2:fori=1 toNdo 3: ifT.size+1>Mthen 4:T0←T 5: ifP<αthen 6:xrand←SAMPLEFREE() 7: else 8:xrand←InformedSample() 9:xnearest←NEAREST(T,xrand) 10:xnew←steer(xnearest,xrand,d) 11: if ObstacleFree(xnew) then 12:xnear←NEAR(xnew) 13: CHOOSEPARENT(xnear,xnew) 14: REWIRE(xnear,xnew) 15: FORCEREMOVAL(T,xnew) 16: if distance(xnew-xgoal) 17: ifM 18:T←T0 19: path=CONNECT(T,xgoal) 20: if environmental change then 21: Replanning() 22:return path 首先,对算法进行初始化,确定初始位置与目标位置,并建立障碍环境。其次,进行采样过程,对于xrand采用带有目标偏向的启发式随机采样: (3) (4) 其中,P为一个随机数,P∈[0,1];α为自定义常数;InformedSample()表示椭球子集采样;d为扩展步长。 采样时,设定一个基准值α,以概率α向目标点方向采样,概率1-α在自由空间内随机采样,保证了搜索目标的随机性和快速性。α的设置根据障碍物确定,当障碍物较少时,α设为较大值;障碍物较多时,α设为较小值。随机树每次在自由空间中采样,按均匀概率分配随机产生一个概率值P。如果P小于原先设定的基准值,则对采样点xrand采用带有目标偏向的随机采样。如果P大于原先设定的基准值,则采样点进行椭球子集约束采样。 完成搜索最近邻近点、扩展新节点等操作后,在障碍环境中规划出机械臂的一条可行路径,机械臂开始按照规划路径运动,环境变化则进行重规划操作。最后,机械臂末端运动到指定位置,运动规划任务完成。改进RRT*FN算法流程如图3所示。 图3 算法流程图Fig.3 Algorithm flow chart 图4 椭球子集采样Fig.4 Ellipsoid subset sampling 此采样过程需要将样本xellipse均匀地分布在子集Xellipse内。通过将样本均匀地分布在一个单位半径为n的球上,然后将xball转移到椭球子集Xball来实现[14]: xellipse=Lxball+xcenter (5) xcenter=(xf1+xf2)/2 (6) Xball={x∈X∣‖x‖2≤1} (7) 其中,xf1和xf2为椭球子集的焦点;‖x‖2为x的二范数,利用超椭球矩阵S∈Rn×n的Cholesky分解得到变换: LLT≡S (8) (x-xcenter)TS(x-xcenter)=1 (9) (10) 经过分解运算得到 (11) 将样本从一个半径为n的球转换为一个n维椭球后,必须旋转到世界坐标系。根据解决Wahba问题的思想[15],旋转矩阵为 C=Udiag(1,…,1,det(U)det(V))VT (12) 其中det()为矩阵行列式,U∈Rn×n、V∈Rn×n通过奇异值分解UΣVT≡M的酉矩阵得出,Σ是主对角线上元素绝对值为1的对角阵,M通过恒等矩阵的第一列的外积和世界坐标系上的横轴长度a1计算得到: M=a1I (13) a1=(xgoal-xstart)/‖xgoal-xstart‖2 (14) 其中,I是单位矩阵。 通过下式得到子集: (15) 椭球子集采样伪代码如下: 1:ifcbest<∞ then 2:cmin←‖xgoal-xstart‖2 3:ccenter←(xstart+xgoal)/2 4:c←RotationToWorldFrame(xstart,xgoal) 5:r1←cbest/2 7:L←diag{r1,r2, … ,rn} 8:xball← SampleUnitBall() 9:xrand←(CLxball+xcenter)∩x 10:else 11:xrand~U(x) 12:returnxrand RotationToWorldFrame()函数生成一个从椭球坐标系到世界坐标系的旋转矩阵,SampleUnitNBall()函数在以原点为中心的单位半径的球内进行均匀采样,最后将xrand映射到椭球内。 在找到目标点后,由于障碍物和目标的位置可能会变化,导致规划好的路径不再适用,所以关键问题是既要使用之前规划生成的树,又要平衡使用上次规划的树和在此规划中取样的新点。针对这些问题,需要对路径进行重新搜索和优化。 对于移动或未知障碍物的路径运动问题,传统重规划的方法是更新环境模型,并在所有障碍物都是静态的情况下重新运行一个新的运动规划过程。该方法将丢弃旧树,并丢失算法运行时生成的有价值信息。丢失的信息包括障碍物碰撞检测例程的结果和通过树搜索配置空间的结果。本文采用对节点剪枝与连接的启发式重规划方法,能保留旧树中的重要信息并尽可能重复利用。 在得到初始解后,若环境变化则执行重规划例程,其伪代码如下: 1:τ←ImprovedRRT*FN(xinit) 2:xcur←xstart 3:σ← SolutionPath(,xcur) 4:InitMovement() 5:whilexcur!=xgoaldo 6:D← UpdateObtacles() 7: if DetectCollision(σ,xcur) then 8: StopMovement() 9:τ← SelectBranch(xcur,τ) 10:xsep← ValidPath(σ) 11: ReconnectFailed ← true 12:xnear← Near(,xsep) 13: forxnear∈xneardo 14: if ObstacleFree(xnear,xsep) then 15:τ←Reconnect(xnear,xsep,τ) 16: ReconnectFailed← false 17: break 18: if Reconnect Failed = true then 19:τ←Regrow(τ,xsep) 20: SetBias(σsep) 21:σ← SolutionPath(τ,xcur) 22: ResumeMovement() 23:path=CONNECT(τ,xgoal) 24:return path 规划路径σ(实现从xinit开始的路径节点的链表)将得到进一步优化,并更好地探索配置空间。然后,机器人开始移动。一旦在σ上到达新的节点xcur,障碍物信息将会更新。如果在xcur和xgoal之间的任何路径段中检测到障碍物碰撞,则机器人停止移动。执行SelectBranch和ValidPath例程,SelectBranch通过移除旧节点从xinit到xcur创建新节点。ValidPath检查先前规划的路径,移除与新障碍物及其碰撞的所有节点,保留连接到xgoal的规划路径的可用部分。这部分称为σsep,从节点xsep开始,到目标节点xgoal结束。 第二阶段包括两个例程Reconnect和Regrow。首先,Reconnect查找σsep中每个节点的附近节点,并判断旧树中的任意节点是否可以连接到这些节点的其中一个。如果存在这样的节点,则旧树重新连接到此路径节点,并删除σsep中所有前面的路径节点。如果Reconnect中找不到规划方案,则执行Regrow。在Regrow中,主树会一直生长,直到xsep中的任何节点都可以重新连接到主树为止。找到规划路径后,将删除未连接到主树上的节点。最后,根据规划方案生成一条新的无碰撞路径,重规划完成。 为了验证本文算法的有效性和可靠性,进行了仿真和实验分析,并与RRT*、RRT*FN、Informed RRT*算法在多场景下进行对比。 3.1.1二维仿真 设置650×650的场景1,将起点设为(50,50),目标点设为(600,600),设置启发式概率α=0.15,步长为5,令固定的最大节点数为1000,最大迭代次数为5000。 如图5所示,绿线部分为搜索形成的随机树,红线部分为规划的路径。通过对比分析搜索时间与路径长度的差异,即可验证改进算法的性能。 (a)RRT* (b)RRT*FN (c)Informed RRT* (d)本文算法图5 场景1中算法测试结果Fig.5 Algorithm test results in scenario 1 经过100组重复实验,实验结果见表1。通过对比可以看出,四种算法在场景1中具有较高的成功率。RRT*FN与本文算法的规划时间较短。为了验证不同的迭代次数对算法路径收敛结果的影响,在场景1中进行测试对比,结果如图6所示。相较于其他三种算法,本文算法具备更短的路径长度和更快的收敛速度。 表1 场景1中算法性能对比Tab.1 Performance comparison of the algorithms in scenario 1 图6 场景1中算法路径收敛结果Fig.6 Path convergence results of the algorithms in scenario 1 相较于场景1,场景2的起点与终点间存在一条狭窄通道,用来验证算法对狭窄通道的搜索能力。将起点设为(50,50),目标点设为(600,600),设置启发式概率α=0.15,步长为5,最大迭代次数为5000。四种算法的实验结果如图7和表2所示。通过对比可以看出,Informed RRT*和本文算法在狭窄通道场景下具有较高的成功率;相较于Informed RRT*算法,本文算法规划路径更短、规划速度更快。 (a)RRT* (b)RRT*FN (c)Informed RRT* (d)本文算法图7 场景2中算法测试结果Fig.7 Algorithm test results in scenario 2 表2 场景2中算法性能对比Tab.2 Performance comparison of the algorithms in scenario 2 相较于场景1和场景2,场景3的环境更为复杂,用来验证算法对动态环境的适应能力。最初将起点设为(50,50),目标点设为(600,600),设置启发式概率α=0.15,步长为5。本文算法的实验结果如图8所示。通过对比图8a、图8b可以看出,当目标点发生改变时,本文算法可以通过重规划进行搜索,最终规划出一条新的无碰撞路径。图8c、图8d中环境发生变化,阻挡了原有规划路线。对比发现,当环境发生改变时算法可以重新规划一条新的无碰撞路径,成功避开障碍物。对比场景3的规划结果得出,本文算法在重规划时,旧树并没有被完全删除,而是通过旧节点的重新采样和扩展来进行搜索,这样大大提高了搜索效率和收敛速度。 (a)初始位置 (b)目标点变化 (c)初始环境 (d)环境变化图8 场景3中本文算法在动态环境的测试结果Fig.8 Test results of the algorithm in this paper in scenario 3 with dynamic environment 3.1.2三维仿真 为了验证本文算法在三维场景中的有效性,搭建了三维空间避障环境,并对规划算法和重规划算法进行了仿真对比验证,如图9所示。 对比图9a、图9b可以看出,RRT*算法的搜索树几乎布满了整个空间,而本文算法以概率α向目标点进行采样,简化了搜索过程,轨迹较为光滑,有效提高了轨迹规划效率。如图9c、图9d所示,当障碍物大小发生变化后,原规划路径无法实现避障任务,本文设计的重规划算法将删减部分原有搜索树并搜索新树,重新规划出一条无障碍路径,证明本文算法能较好地适应动态环境并完成避障任务。 (a)RRT* (b)本文算法 (c)初始环境 (d)环境变化图9 三维环境规划结果Fig.9 3D environmental planning results 为了进一步验证本文算法在虚拟环境中的有效性,建立了七自由度机械臂模型,并用本文算法对其进行了运动规划仿真实验。如图10所示,实验结果表明本文算法可以有效应用于虚拟环境。 (a)虚拟环境 (b)规划结果图10 虚拟环境规划结果Fig.10 Virtual environment planning results Sawyer机器人是Rethink Robotics公司推出的智能协作机器人,具备七自由度,能够适应狭窄和复杂空间的作业环境。利用机器人操作系统(ROS)对Sawyer机械臂进行仿真环境配置,并将本文算法用于Sawyer机械臂的运动规则,结果如图11所示。通过对比实验结果可以看出,机械臂在狭窄通道、障碍物环境以及环境变化时,能够快速规划路线并成功地从起始位置到达目标位置。 (a)狭窄通道 (b)狭窄通道规划结果 (c)复杂环境 (d)复杂环境规划结果 (e)动态环境 (f)动态环境规划结果图11 ROS仿真规划结果Fig.11 ROS simulation planning results 图12所示为Sawyer机械臂在真实环境下的运动规划验证实验。设定白色长方体盒为障碍物,左侧位置为起始点,目标是避开障碍物将其移动到另一侧的魔方位置。在路径规划完成后,将得到的路径信息发送至机械臂控制器,从而实现机械臂从起始位置经过一条无碰撞的路径到达目标位置的规划任务。由图12可以看出,本文算法在真实环境中能够有效完成避障任务,证明了本文算法的实用性。 (a)初始环境 (b)环境变化图12 真实环境下的避障过程Fig.12 Obstacle avoidance process in actual environment 本文提出了一种改进RRT*FN机械臂多场景运动规划算法。针对基本RRT*FN算法的缺陷进行了两点改进: (1)结合目标偏向随机采样和椭球子集采样的优势,提出新的启发式采样方法对采样区域进行约束,从而保证路径收敛速度更快,搜索路径更优。 (2)在动态环境下,不需要完全重新规划,而是采用对旧节点重新剪枝与连接的启发式重规划方法,提高了算法对环境的适应能力,规划效率更高。 与传统RRT*、RRT*FN、Informed RRT*算法相比,本文算法在规划过程中收敛速度更快、规划效率更高,在狭窄通道环境中成功率更高。在障碍物环境变化或目标点改变时,可以快速地适应环境,并能够有效实现机械臂的快速运动规划。1.2 碰撞检测
2 改进RRT*FN算法
2.1 基本RRT*FN算法
2.2 改进RRT*FN算法
2.3 椭球子集采样
2.4 重规划
3 仿真与实验分析
3.1 仿真分析
3.2 实验分析





4 结论

