基于坡面卸荷的土质边坡应力状态及稳定性分析

杨奎斌，朱彦鹏

(1. 兰州理工大学土木工程学院，甘肃，兰州 730050；2. 西部土木工程防灾减灾教育部工程研究中心，甘肃，兰州 730050)

边坡稳定性分析是土力学中的经典问题之一，而坡体应力状态作为影响边坡稳定性的一个重要因素，长期以来备受专家学者关注。卢应发等[1]根据坡体变形和力的传递特征，认为边坡滑面在不同位置表现出不同的应力状态特征；苏杭等[2]基于边坡施工后坡体位移的相对变化趋势，给出了边坡开挖松弛区和预压区的明确定义；王浩等[3]解释了路堑高边坡开挖卸荷松弛的力学机理，模拟重现了边坡失稳破坏阶段的全过程应力调整规律及发展趋势；冷伍明等[4]、艾希等[5]为有效改善路堤填土应力状态，提出了一种新型预应力路基结构，并分析了坡面法向、水平向附加应力扩散规律；李丽华等[6]对废旧轮胎加筋路堤边坡进行模型试验，认为轮胎加筋可显著改变坡体应力状态，有利于增强边坡稳定性；陈金锋和宋二祥[7]在山区机场高填方边坡建设中提出了单级反压护道的优化设计方法，其理念实质也是通过反压改变坡体受力状态，进而提高边坡稳定性。由此可见，无论是边坡开挖卸荷还是支护加载，均与坡体应力重分布密切相关，基于应力状态对边坡稳定性进行研究很有实际意义。

在现有边坡稳定分析方法中，利用条分法建立的极限平衡理论最早产生，根据条间力假设的不同，相继又有多种不同方法被提出，这些方法概念清晰、计算简便，在工程中被广泛应用，然而刚性土条假设无法反映坡体应力场分布情况，且条间力假设所产生的分析误差始终难以避免。为解决这一问题，部分学者在不引入条间力的情况下，取整个滑体为研究对象，并基于滑面应力假设和修正建立平衡方程进行安全系数求解[8-12]。与此同时，一些学者还借助数值软件获取坡体真实应力场，进而根据滑面应力进行边坡稳定性分析。其中邵龙潭等[13]基于有限元滑面应力分析法对重力式挡土墙进行研究，搜索确定了最危险滑动面和对应的安全系数；吴顺川等[14]根据滑面应力状态提出了边坡安全系数新解法，能够有效解决非等比强度折减方案中边坡稳定性评价指标的确定；张海涛等[15]给出了矢量和的滑面应力抗滑稳定分析新思路以及矢量和形式的安全系数；李忠等[16-17]通过建立边坡非线性有限元计算模型，提出了基于滑面应力控制的边坡主动加固计算方法，并将有限元计算与多种群遗传算法结合，建立了一种基于MPGA 的复杂应力状态边坡稳定性分析通用模型；Stianson 等[18]利用有限元所得应力对边坡稳定性进行研究，总结了土体泊松比和弹性模量对稳定性安全系数的影响规律；Liu 等[19]将有限元应力场用于多种不同类型边坡，进一步拓宽其在边坡稳定性分析中的适用性。显然，以上这些方法为边坡稳定性研究提供了很好的思路，但利用条分法建立的极限平衡理论始终难以考虑土体应力状态，坡体滑面应力计算又长期停留在数值方法上。

为了有效获取坡体应力状态，本文基于坡面卸荷应力等效思路，将边坡视为水平地面经开挖后形成的坡体，并利用弹性理论对坡内土体任一点进行应力求解，进而根据滑面应力计算边坡稳定性安全系数，最后结合多个算例对潜在滑动面位置及稳定性安全系数进行比较来验证其合理性。

1 坡面卸荷应力等效分析思路

具有一定高度和坡度，存在临空面的坡体，可以将其认为是自然水平地面经开挖后形成的斜坡。当开挖部分挖除卸荷后，原本作用在坡面上的应力将得到释放，所以坡体内任一点应力由两部分组成：一部分是开挖前自然水平地面所对应的竖向自重应力和水平自重应力；另一部分则是卸荷引起的应力改变量。

需要说明的是，坡面卸荷是一个应力释放、应力重分布过程，在坡面处的卸荷等效应该采用应力等效，而非荷载等效，如图1 所示。后者被苏联专家弗洛林 B·A[20]在《土力学原理(第一卷)》中提到，笔者认为两者在本质上存在不同，应力等效较荷载等效更为合理。

图1 坡面卸荷应力等效示意图Fig. 1 Stress equivalent diagram of slope unloading

坡面上任一点竖向和水平向卸荷应力可根据土力学按深度求得，其中均质土按下式计算，成层土则进一步考虑每层土性质。

式中： γ为土体重度；y为坡顶面以下深度；K0为土的侧压力系数，理论上有K0=ν/(1-ν)，ν为土的泊松比。

为方便计算，取坡面土单元进行受力分析时，可将卸荷等效应力转换为作用于坡面的法向应力 σα和切向应力τα，其沿坡面分布如图2 所示。

图2 坡面等效应力分布Fig. 2 Equivalent stress distribution of slope surface

显然，只要计算出图2 中坡面卸荷应力对坡体内应力的改变量，即可获得重分布后的坡体应力场，进而以此得到潜在滑动面上的应力状态。

2 坡体内一点应力计算

对于二维边坡而言，可以将其视为平面应变问题，这样在进行坡面卸荷应力释放量计算时，能够将坡面按弹性半无限边界考虑，并采用弹性理论进行附加应力积分处理，具体计算过程如下。

2.1 计算模型与参数

根据式(1)～式(4)可将坡面线上任一点切向力和法向力简化如下：

2.2 坡面法向卸荷应力作用下的附加应力

本文以压应力为正，剪应力则以使单元体逆时针旋转为正，反之为负，半无限体在边界上受法向集中力时如图3 所示。

图3 半无限体边界受法向集中力Fig. 3 Normal force on boundary of semi-infinite body

图3 中任一点附加应力计算公式可根据弹性半无限体在边界上受法向集中力作用的Boussinesq解[21]在无限长范围内积分得到的Flamant 解[22]确定，也可利用楔形体楔顶受集中荷载作用的弹性应力解[23]确定：

在x′oy′坐标系下对式(7)～式(9)进行坡面范围内积分，可得坡面法向卸荷应力作用下坡体内附加应力值，具体求解根据积分式采用MATLAB 中的int 函数进行。

式中：b为坐标原点至坡脚的距离； η为坡面任一法向应力作用点至坐标原点的距离；x′、y′为x′oy′坐标系内任一点坐标。

图4 坡面受法向应力作用分析模型Fig. 4 Analysis model of normal stress on slope surface

2.3 坡面切向卸荷应力作用下的附加应力

同理，半无限体在边界上受切向集中力时如图5 所示，任一点的应力计算公式为[23]：

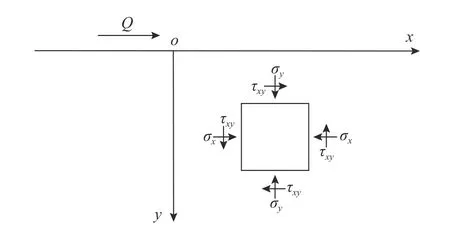
图5 半无限体边界受切向集中力Fig. 5 Tangential force on boundary of semi-infinite body

图6 坡面受切向应力作用分析模型Fig. 6 Analysis model of tangential stress on slope surface

2.4 xoy坐标系内坡体应力转化

在x′oy′坐标系内，坡体内任一点卸荷应力改变量为坡面法向、切向卸荷应力所引起的附加应力之和。

3 稳定性分析方法

3.1 潜在滑动面形式选择

通过对圆弧、对数螺旋线等现有潜在滑动面曲线形式，以及相应搜索方法的比较，笔者提出了搜索量小，易于编程，且具有一定物理意义的最速降线形滑动面，由于篇幅有限，在此不再赘述，具体搜索模型如图7 所示。

图7 边坡潜在滑动面搜索模型简图Fig. 7 Sketch of searching model for potential sliding surface of slope

图7 中线段OA、OB为边坡表面，曲线AM为最速降线滑动面，以点O为坐标系原点，当M点的坐标为 (m,0) 时，潜在滑动面曲线AM的参数方程如下：

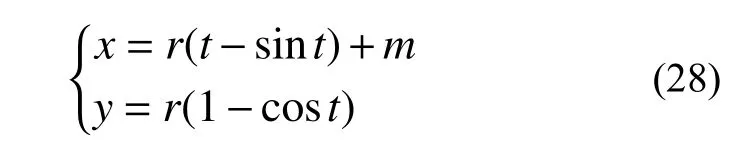
式中：r为最速降线对应的旋转圆半径；t为旋转圆转动经过的角度。

显然，要确定最速降线滑动面参数方程需要求得r，以及自变量t的取值范围，其求解过程如下：

1) 将滑出位置A点坐标 (a,b)代入滑动面参数方程可求得滑出点处自变量的边界值t′，由此得出自变量t的取值范围为 (t′,0)。

2) 再将滑出点坐标 (a,b)及滑出点处自变量的边界值t′代入参数方程，即可求得r值。

搜索过程中，假定滑动面经过坡脚，由此便可通过移动M点位置进行潜在滑动面搜索。

3.2 滑面应力计算

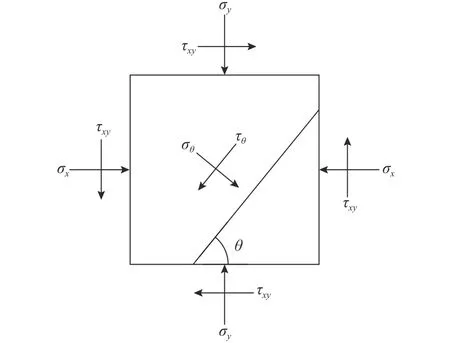
图8 滑面单元应力分析模型Fig. 8 Analysis model of stress on an element of slip surface

式中， θ为xoy坐标系内滑动面切线与x轴夹角。

3.3 安全系数计算

4 算例分析

4.1 未支护均质土坡

4.1.1 算例概况

为说明坡面卸荷应力等效思路在边坡稳定性分析中的可行性，选用多个文献[24 - 26]中均用到的一个经典边坡算例进行分析比较，边坡高度20 m，坡度为45°。这里为便于观察比较，取坡脚处为坐标原点，滑面应力计算仍按2.2 节和2.3 节坐标系进行，具体计算模型如图9 所示，岩土材料参数如表1 所示。

说到吴琮，夏霖和他虽然是同桌，但平时并没有太多来往。主要的原因是，夏霖很多次找他说话，他都不予理会，吴琮给人的感觉就是“高冷”。而且在夏霖的印象中，她从没见过吴琮和谁要好，他总是独来独往，像个透明人一样，常常被大家视而不见。

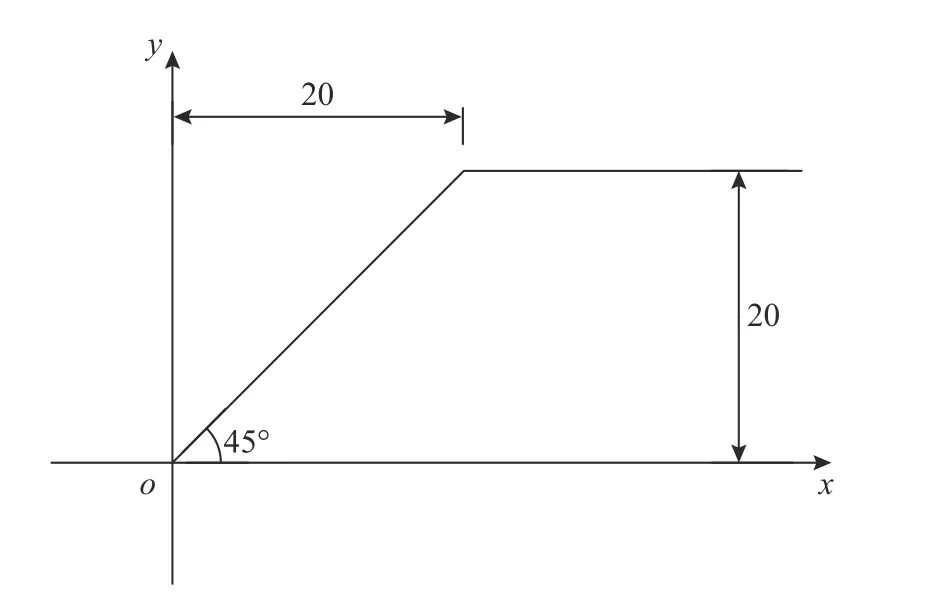
图9 算例1 的边坡尺寸 /mFig. 9 Slope size of classical Model 1

表1 算例1 的材料参数Table 1 Material parameters of Model 1

4.1.2 滑动面位置及安全系数比较

借助MATLAB 编制计算程序，实现沿坡顶面移动滑入点位置进行滑动面搜索，最终寻找出最小安全系数对应的潜在滑动面，经搜索得到安全系数随滑入点位置变化情况，如图10 所示。

从图10 中可以看出，当滑入点距坡顶边缘8 m左右时安全系数最小，通过进一步提高搜索精度，得到边坡潜在滑动面滑入点位置为(27.7，20)，稳定性安全系数为1.148。与此同时，为验证计算结果的合理性，将其与已有文献和极限平衡法相应结果进行比较，其中潜在滑动面位置比较如图11 所示，稳定性安全系数对比如表2 所示。

图10 安全系数与搜索位置关系曲线Fig. 10 Relationship curve between safety factor and search location

图11 不同方法潜在滑动面位置比较Fig. 11 Comparison of potential sliding surface positions obtained by different methods

表2 不同计算方法所得安全系数对比Table 2 Comparison of safety factor from different calculating methods

结合图11 和表2 可以看出，基于坡面卸荷应力等效思路所得结果与传统方法计算结果基本一致，其中潜在滑动面位置吻合度较好，滑入点较极限平衡法所得位置略有前移。稳定性安全系数方面，较已有文献以及极限平衡法结果略微偏小，分析认为有以下几点原因：

1)坡体内应力求解时将坡面按弹性半无限边界进行假设，所得滑面应力存在一定偏差，会影响到稳定性安全系数值。

2)有限元方法虽然能够充分考虑土体应力-应变关系，但在边坡稳定性分析时采用的强度折减法却存在着一些不足[27]，尤其在折减方法及失稳别标准上，尚未形成统一，受人为因素影响较大。

由上述分析可以看出，经典算例所得结果与强度折减法、极限平衡法吻合度较好，但坡面按弹性半无限边界假设对计算结果有一定影响。为说明其影响程度，并充分验证坡面卸荷应力等效思路在边坡稳定性分析中合理性，有必要在经典算例基础上继续对滑面应力进行比较，以及采用更多衍生算例对安全系数影响因素作进一步讨论。

4.1.3 滑动面应力比较

选用有限元软件Plaxis 开展数值模拟，进行坡体内应力值对比，尤其是滑面应力比较，其中土体材料模型采用Mohr-Coulomb，考虑到计算精度要求，模型下边界为坡脚以下10 m，左边界为坡脚向左10 m，右边界为坡顶向右30 m，网格密度为很细，有限元模型如图12 所示。

图12 经典算例有限元模型Fig. 12 FE model of classical example

经计算，得到能够反映潜在滑动面特征的增量位移云图，如图13 所示，对应的稳定性安全系数为1.157，这与4.1.2 节分析的滑动面位置和安全系数大小一致，说明基于此模型进行滑面应力比较合理可行。因此，在基于坡面卸荷应力等效思路搜索得到的潜在滑动面上选取3 个参考点，与有限元模型相应位置应力进行比较，其中point1位于滑面下部，point2 位于滑面中部，point3 位于滑面上部，如图14 所示，所得参考点应力值如表3所示。

图13 模型增量位移云图Fig. 13 Incremental displacement nephogram of model

图14 滑面应力参考点选取Fig. 14 Selection of reference points of stress on sliding surface

从表3 中可以看出，坡体按弹性半无限体计算得到的竖向应力和滑面中下部剪应力与有限元结果接近，水平向应力与有限元结果存在偏差。分析认为这种偏差由坡面卸荷应力等效和坡面半无限体假设共同造成，主要是因为边坡临空面的存在使得水平向应力计算受假定条件影响较大。但总体来看，竖向应力相较于水平向应力、剪应力而言数值明显偏大，在应力状态中具有主导作用，经变换后得到的滑面法向应力、切向应力与有限元结果相差不大。

表3 参考点应力对比 /kPaTable 3 Stress comparison at reference points

为全面掌握滑面应力分布情况，沿滑面将计算得到的法向、切向应力与自重应力、有限元相应结果进行比较，其中自重应力由滑面以上土体自重沿滑面法向和切向分解后得到。由此滑面法向应力分布如图15 所示，滑面切向应力分布如图16所示。

图15 滑面法向应力比较Fig. 15 Comparison of normal stress on sliding surface

经图15、图16 比较可以看出，三种计算方法得到的滑面法向应力与切向应力变化规律相同，均是在滑面中部应力最大，但应力分量数值大小存在一定差异。总体看来，按弹性半无限体求得的滑面应力介于自重应力分量与有限元所得应力之间，与有限元结果接近，与自重应力分量相差甚远。由此说明，不能将滑面应力简单的视为自重应力分量，而按弹性半无限体进行滑面应力计算实际可行，这一点也验证了王邓峮等[28]、雷军和肖世国[29]将坡面视为弹性半无限边界后按弹性理论进行预应力锚杆附加应力分析是正确的。

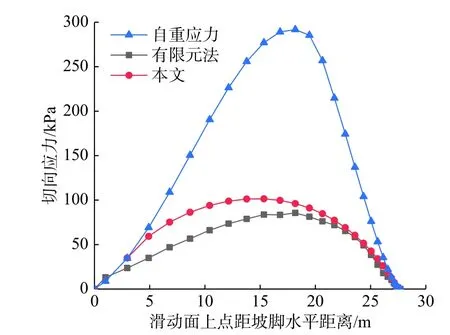
图16 滑面切向应力比较Fig. 16 Comparison of tangential stress on sliding surface

4.1.4 坡率对安全系数影响比较

取高度为20 m，坡率依次为1∶0.3、1∶0.4、1∶0.5、1∶0.6、1∶0.7、1∶0.8、1∶0.9、1∶1.0、1∶1.1、1∶1.2、1∶1.3 的边坡进行比较分析，岩土材料参数仍然采用4.1.1 节中给出的参数。经计算，得到安全系数随坡率变化的对比关系如图17所示。

图17 坡率变化时安全系数比较Fig. 17 Comparison of safety factor with slope rate change

从图17 中可以看出，当滑面曲线形式同为最速降线时，基于坡面卸荷应力等效思路所得安全系数较极限平衡法偏小，相差在8%以内，有限元强度折减法计算结果则介于两者之间。当坡度系数小于0.8 时，Plaxis 显示土体将要坍塌，只能说明安全系数小于1，无法得到具体数值，这一点与本文计算所得安全系数小于1 相一致；当坡度系数大于0.8 时，有限元结果也与本文计算所得安全系数十分接近，相差在3%以内。

4.1.5 坡高对安全系数影响比较

取坡度为45°，坡高依次为5 m、8 m、11 m、14 m、17 m、20 m、23 m、26 m 和29 m 进行比较分析，岩土材料参数仍然采用4.1.1 节中给出的参数。经计算，得到安全系数随坡高变化的对比关系如图18 所示。

从图18 中可以看出，基于坡面卸荷应力等效思路所得安全系数始终与有限元强度折减法计算结果接近，相较于极限平衡法而言偏小，但随着坡高的增加，计算值越来越接近。

图18 坡高变化时安全系数比较Fig. 18 Comparison of safety factors with slope height change

4.2 预应力锚杆支护边坡

选用文献[28]中用到的一个预应力锚杆支护边坡进行分析比较，边坡高度8 m，坡度为90°，土体参数如表4 所示，锚杆布置如图19 所示，每根锚杆施加相同的预应力。

表4 算例2 的土体参数Table 4 Material parameters of Model 2

图19 算例2 的边坡锚杆布置图 /mFig. 19 Prestressed anchor rod layout of slope in Model 2

该算例中除了要计算坡面卸荷引起的应力改变量，还要考虑预应力锚杆作用，因此将预应力分解为水平方向及竖直方向两个集中力后，按半无限体进行附加应力计算。

当预应力从10 kN 增加到100 kN，对算例2进行稳定性安全系数计算，并将计算结果与文献[28]进行比较，如图20 所示。

图20 预应力变化时安全系数比较Fig. 20 Comparison of safety factors with prestress change

从图20 中可以看出，随着预应力的增加，安全系数提高明显，说明锚杆预应力对提高边坡稳定性十分有效。同时，所得稳定性安全系数整体与已有研究结果十分接近。对比图17 中采用极限平衡法所得圆弧和最速降线结果可知，安全系数受坡度影响，当坡度较大时，最速降线所得安全系数略小于圆弧相应结果，当坡度较小时，最速降线所得安全系数略大于圆弧相应结果。本算例中安全系数略大于文献[28]中的相应结果与坡度为90°有关。

5 结论

通过坡面卸荷应力等效思路的提出，将坡面按弹性半无限边界考虑进行坡体内应力求解和稳定性安全系数计算，并多个算例对其合理性验证，得出以下几点结论。

(1)坡面卸荷应力等效思路概念清晰，符合边坡受力特征，能够体现临空面这一决定边坡稳定性的实质特征，同时，将坡面按弹性半无限边界考虑可以有效求得坡体内任一点应力释放值，从而使得边坡稳定性分析不再局限于条分极限平衡法和数值有限元法。

(2)基于坡面卸荷应力等效思路求得的滑面应力与有限元分计算结果基本一致，搜索得到的潜在滑动面位置，以及对应的稳定性安全系数与有限元强度折减法、极限平衡法计算结果十分接近。

(3)在锚杆支护边坡稳定性分析中，该计算方法可以有效与支护结构预应力结合，将坡面卸荷与锚杆预应力施加一并考虑，既能反映坡体临空面的存在，又能体现锚杆预应力的加固作用。

(4)基于坡面卸荷应力等效思路进行的边坡应力计算及稳定性分析主要适用于土质边坡，包括均质土边坡、成层土边坡和预应力锚杆支护土质边坡，对于含有顺坡结构面的岩、土复合边坡并不适用。