主余震序列作用下结构增量损伤比研究

周 洲，于晓辉，吕大刚

(1. 哈尔滨工业大学，结构工程灾变与控制教育部重点实验室，黑龙江，哈尔滨 150090；2. 哈尔滨工业大学，土木工程学院智能防灾减灾工业与信息化部重点实验室，黑龙江，哈尔滨 150090)

一次主震的发生往往可以激发多次余震，其中不乏具有较大强度的余震。这些强余震甚至会造成比主震更大的结构损伤和人员伤亡。例如：发生在2010 年的新西兰克赖斯特彻奇的7.1 级主震并未造成人员伤亡，但在2011 年发生的6.3 级强余震却导致了146 人遇难和300 人失踪[1]的严重后果。大量历史地震资料表明，余震往往会给主震损伤结构带来不可忽视的“二次损伤”，本文称之为“余震增量损伤”。然而，国内外现行抗震规范仅考虑一次地震作用，并未充分考虑余震影响，且对余震对结构造成的增量损伤考虑不足[2]。因此，有必要对余震增量损伤进行全面评估。

近年来，国内外学者分别以单自由度体系和多自由度体系为研究对象，对主余震序列作用下的结构损伤进行了大量研究。例如：Amadio 等[3]研究了单自由度体系在重复型主余震序列作用下的结构损伤，研究发现，结构在经历多次地震作用后发生了较明显的累积损伤。Hatzigeorgiou 等考虑了场地类别、结构延性、结构阻尼比等因素的影响，获得了主余震序列作用下的非线性位移系数谱[4]、延性需求谱[5]和非弹性位移比谱[6]。Zhai等[7]和于晓辉等[8-9]分别开展了主余震序列作用下的结构累积损伤谱和增量损伤谱的研究。Yu等[10]进一步研究了主余震序列作用下的结构抗倒塌能力谱。针对多自由度体系，我国研究学者欧进萍和吴波[11]较早地对钢筋混凝土结构在主余震序列作用下的损伤演化规律进行了研究，定量分析了余震对结构损伤的影响。张昊宇等[12]在尼泊尔8.1 级地震的震害调查中发现，主震后的一次7.5 级强余震导致许多框架结构发生了倒塌。李洪泉等[13]通过对钢框架结构进行振动台实验，研究了反复地震作用下钢框架的累积损伤和剩余强度，研究表明，多次地震作用可以导致结构最大层间位移倍增。袁辉辉等[14]通过拟动力试验，研究了钢管混凝土格构柱在主余震作用下的抗震性能，试验表明，主余震作用会加剧结构的累积损伤。韩建平和李军[15]研究了主余震序列对低延性结构易损性的影响，结果表明，结构的主震损伤越大，余震对结构的破坏力越大。周洲等[16]以一栋5 层钢筋混凝土框架结构为研究对象，分析了主余震序列构造方法对结构易损性的影响，结果表明，主余震易损性曲线明显高于主震易损性曲线，揭示了余震对结构安全的影响。Goda 等[17-18]分析了木框架结构在主震和主余震序列作用下的损伤和易损性曲线的影响，结果表明，余震将结构的延性需求参数提高了5%～20%，并能较显著地提高结构的易损性水平。此外，Iervolino 等[19]采用马尔科夫链方法揭示某六层钢筋混凝土框架结构在主余震序列作用下结构损伤的演化规律。上述基于非线性单自由度体系和多自由度体系的研究结果均表明，主余震序列会造成明显的结构累积损伤，余震给主震损伤结构所造成的增量损伤不可忽视。

目前，在分析结构主余震损伤所较常采用的结构损伤指标主要是最大层间位移角和残余层间位移角[20]。作为位移型结构损伤参数，最大层间位移角和残余位移角在评估结构主余震损伤中存在以下两点问题：1) 不具有单调递增的特性，无法准确量化余震在主震损伤基础上造成的增量损伤[21-22]；2)存在“极性(polarity)”[20]的问题(主余震损伤的方向性问题)，主震损伤与余震损伤的方向可能不一致。

鉴于上述两点问题，本文采用能量型损伤参数来量化结构在主余震序列作用下的累积损伤。能量型损伤参数可以较好地解决位移型损伤参数存在的无单调递增性和极性的问题。由Park 和Ang[23]提出的损伤参数(以下简称Park-Ang 损伤参数)是一种较为常用能量型的地震损伤参数，已被广泛用于主余震序列作用下结构损伤评估[8-9]。由于Park-Ang 损伤参数具有单调递增性，故可以将主震和余震作用下的结构损伤进行累加，从而方便量化余震增量损伤。目前，国内外对于余震造成的结构增量损伤的准确预测还研究较少，这不利于合理评估主余震联合作用对结构地震损伤的影响。

为弥补现有研究对余震增量损伤的考虑不足，本文选用一组单自由度体系作为研究对象，以较大数量真实主余震序列记录作为地震动输入，采用Park-Ang 损伤指数来量化结构在主余震序列作用下的主震损伤和余震增量损伤。本文提出“增量损伤比”这一参数以量化余震对主震损伤结构的“二次损伤”，通过建立其与余震和主震强度比以及周期的相互关系，提出增量损伤比的预测模型，并对预测模型的影响因素进行讨论。

1 非线性单自由度体系的建模

考虑4 种恢复力模型来模拟非线性单自由度体系的非线性行为，如图1 所示。其中，Model-1为基准模型，为理想弹塑性模型；Model-2、Model-3、Model-4 分别代表在基准模型Model-1中附加考虑P-Δ效应、捏缩效应和强度退化效应。图中，Fc和Fy分别为结构的极限强度和屈服强度；δc和δy分别为极限位移和屈服位移；Ke为弹性刚度；θ 为调整系数。模型参数的详细取值参见文献[24]。

图1 单自由度体系的骨架曲线Fig. 1 Backbone of SDOF systems

在上述四类恢复力模型中，考虑不同强度折减系数Ry的影响。Ry可表示为：

式中，Fm和Fy分别表示结构在地震作用下的反应力峰值和屈服强度。

结构的自振周期T的计算范围为0.1 s～6.0 s。其中，在短周期和中长周期范围内(T=0.1 s～3.0 s)，计算用结构周期间隔取为0.1 s；在长周期范围内(T=3.0 s～6.0 s)，计算用结构周期间隔取为0.2 s。根据《建筑结构荷载规范》[25]，普通高层钢筋混凝土结构的基本周期为T1=(0.05～0.10)n，其中，T1为建筑的基本周期，n为建筑层数。长周期范围T=3.0 s～6.0 s 可对应30 层以上的高层建筑。因此，本文所考虑的长周期范围T=3.0 s～6.0 s 可涵盖一般结构的长周期范围。此外，根据已有的相关研究[8,10,24,26]，本文将结构阻尼比取为ξ=0.05，该阻尼比对应量大面广的钢筋混凝土结构。

2 真实主余震序列的挑选

按照文献[24]，本文从太平洋地震工程研究中心的PEER NGA-West 强震地震动数据库中(https://peer.berkeley.edu/nga-west)选取662 条真实主余震记录作为地震输入，其所对应的地震事件基本信息，如表1 所示。在主余震记录挑选的过程中，遵循以下两点原则：1)主震记录和余震记录须出自同一台站；2)仅挑选余震序列中震级最大的一次余震用于构造主余震序列。本文所挑选的主余震记录中，主震震级区间为[5.8, 7.62]，余震震级区间为[5.01, 7.14]，主震震级均大于余震震级。主、余震地震动的其他详细信息请见文献[24]。

表1 主余震事件基本信息Table 1 Information of mainshock-aftershock events

为使结构在主震作用后可以恢复到新的平衡状态，在主余震序列的构造过程中，在主震和余震记录之间加入100 s 的时间间隔[10]。受地震动监测仪器的频率范围所限，每条地震动记录均存在一个最低使用频率flow。则该地震动所能适用的最大结构周期为T=1/flow。对于一条给定的主余震序列，选取主震和余震记录所对应的flow值的较大值作为该主余震序列的flow值。

3 主余震序列作用下结构损伤分析

3.1 Park-Ang 损伤指数

为定量描述结构在主余震序列作用下的损伤，本文选取Park-Ang 指数[27]DI作为结构损伤参数：

式中：umax、uy和uu分别为结构的最大位移、屈服位移和极限位移；EH为地震作用下的结构滞回耗能；Fy为结构的屈服强度；β 为耗能因子，取β=0.15[7]。

3.2 主震损伤、余震增量损伤和主余震累积损伤

采用第2 部分中所挑选的真实主余震记录作为地震输入，对考虑不同恢复力模型的非线性单自由度体系进行时程分析，获得了结构的主震损伤DIM和余震增量损伤DIA。将主震损伤DIM和余震增量损伤DIA进行累加可获得非线性单自由度体系的主余震累积损伤DIMA。主震损伤DIM、余震增量损伤DIA和主余震累积损伤可按式(3)～式(5)计算。图2 给出了DIM、DIA和DIMA的计算过程。

图2 主震损伤、增量损伤和累积损伤的计算Fig. 2 Calculation for DIM, DIA and DIMA

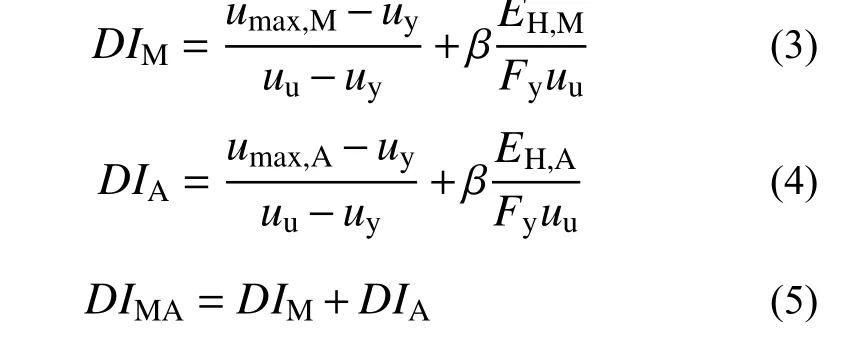
式中：umax,M和EH,M分别为主震作用下结构的最大位移和滞回耗能；umax,A和EH,A分别为余震作用下结构的最大位移和滞回耗能。

本节以Model-1 在T=1.0 s 和Ry=2 条件下的计算结果为例，获得结构的DIM、DIA和DIMA三者之间的关系，如图3 所示。

由图3(a)可以看出，随着DIM的提高，DIA的幅值和离散程度也随之提高。这说明，主震损伤结构的余震增量损伤与其初始损伤的大小相关性很强。由图3(b)可以看出，DIA的幅值和离散程度同样随着DIMA提高而提高。此外，由于余震增量损伤的附加作用，DIMA要明显高于DIM，部分数据表明，结构在主震单独作用下未倒塌，而在余震附加作用下却发生倒塌的现象。由图3 还可见，由于余震增量损伤离散性随着主震损伤的提高而提高，因此，DIA无法直接通过DIM和DIMA进行合理预测。

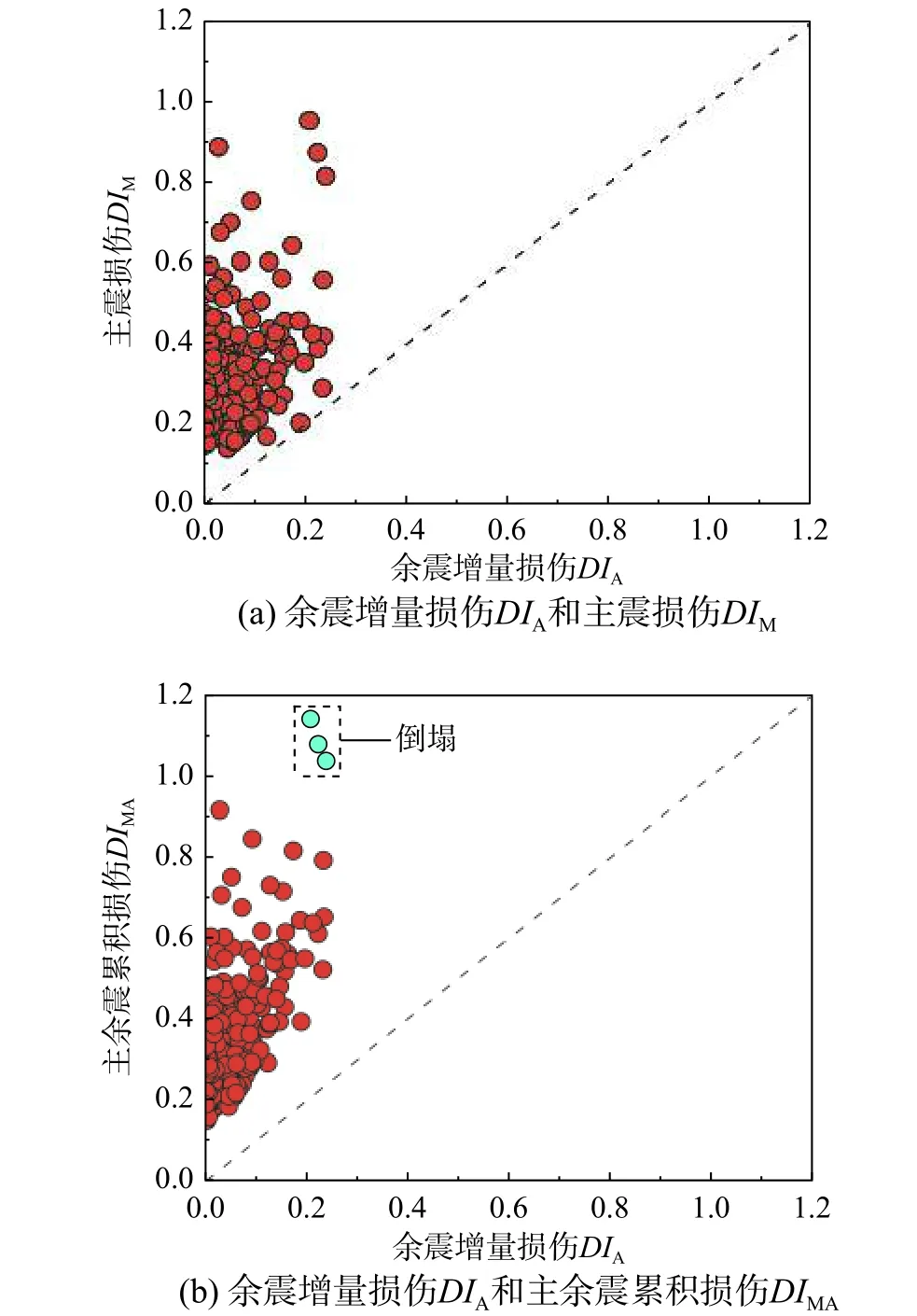
图3 主震损伤、主余震累积损伤和余震增量损伤的关系Fig. 3 Relationship between DIA and DIM and that between DIA and DIMA

3.3 增量损伤比

4 增量损伤比的预测

4.1 主余震强度比

在已有的相关研究中，多采用主、余震强度极值(如：采用主震PGA 和余震PGA 的较大值来代表主余震序列PGA)或单纯采用主震或余震强度来作为主余震序列强度[29]。Zhou 等[24]研究表明：主余震序列强度或单纯主震或余震强度与余震增量损伤的相关性较弱，但主余震强度比(余震强度与主震强度的比值)与增量损伤比的相关性较强，要明显优于单独主、余震强度参数。为此，本文引入主余震强度比来进行结构增量损伤比的预测。主震、余震强度比按下式计算：

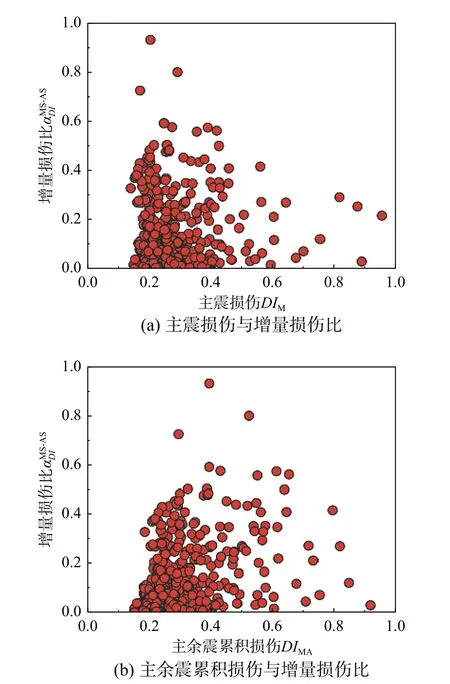
图4 主震损伤、主余震累积损伤与增量损伤比Fig. 4 Relationship betweenDIM and ln(αMDIS-AS) and that between DIMAand ln(α

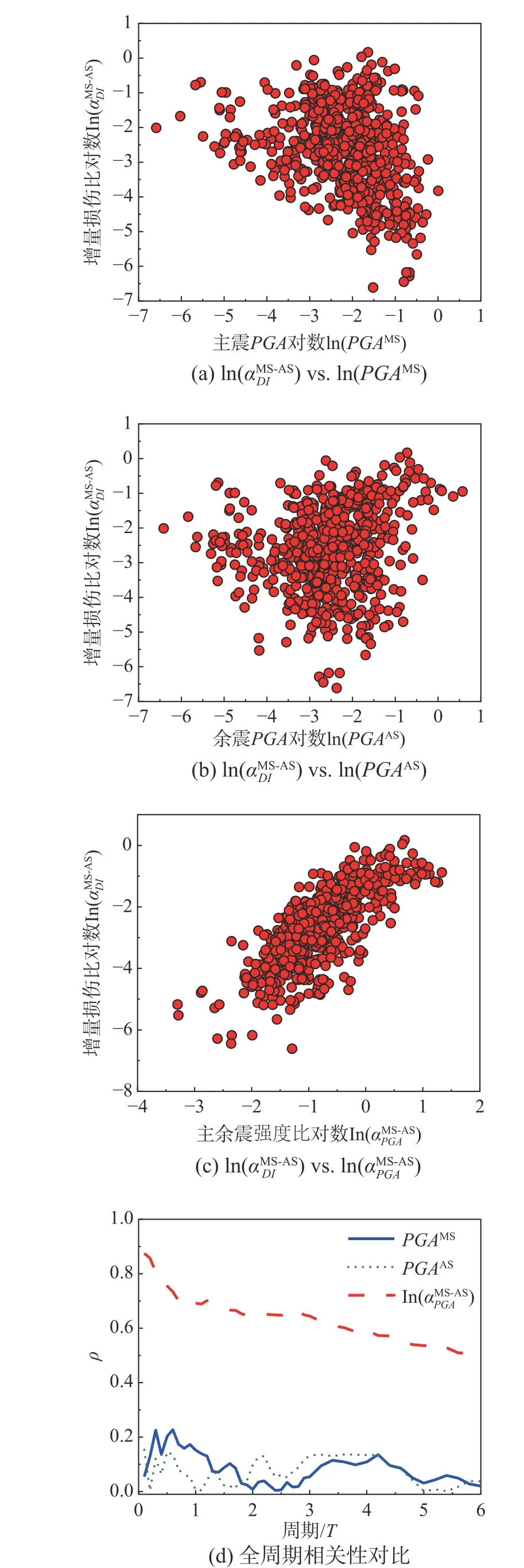
图5 ln(PGAMS)、ln(PGAAS)、 和 关系Fig. 5 Relationship among ln(PGAMS), ln(PGAAS),and

4.3 增量损伤比的预测模型

图6 A 与 和与的线性相关性Fig. 6 Linear correlation of and

图7 展示了Model-1～Model-4 在Ry=2 时的增量损伤比预测结果与真实计算结果的对比。由图7可以看出，采用式(8)的所示的增量损伤比预测模型，可以较好地拟合计算结果，预测模型的拟合优度判决系数R2要高于0.7。表2 展示了Model-1～Model-4 在不同Ry的条件下的预测模型拟合结果。

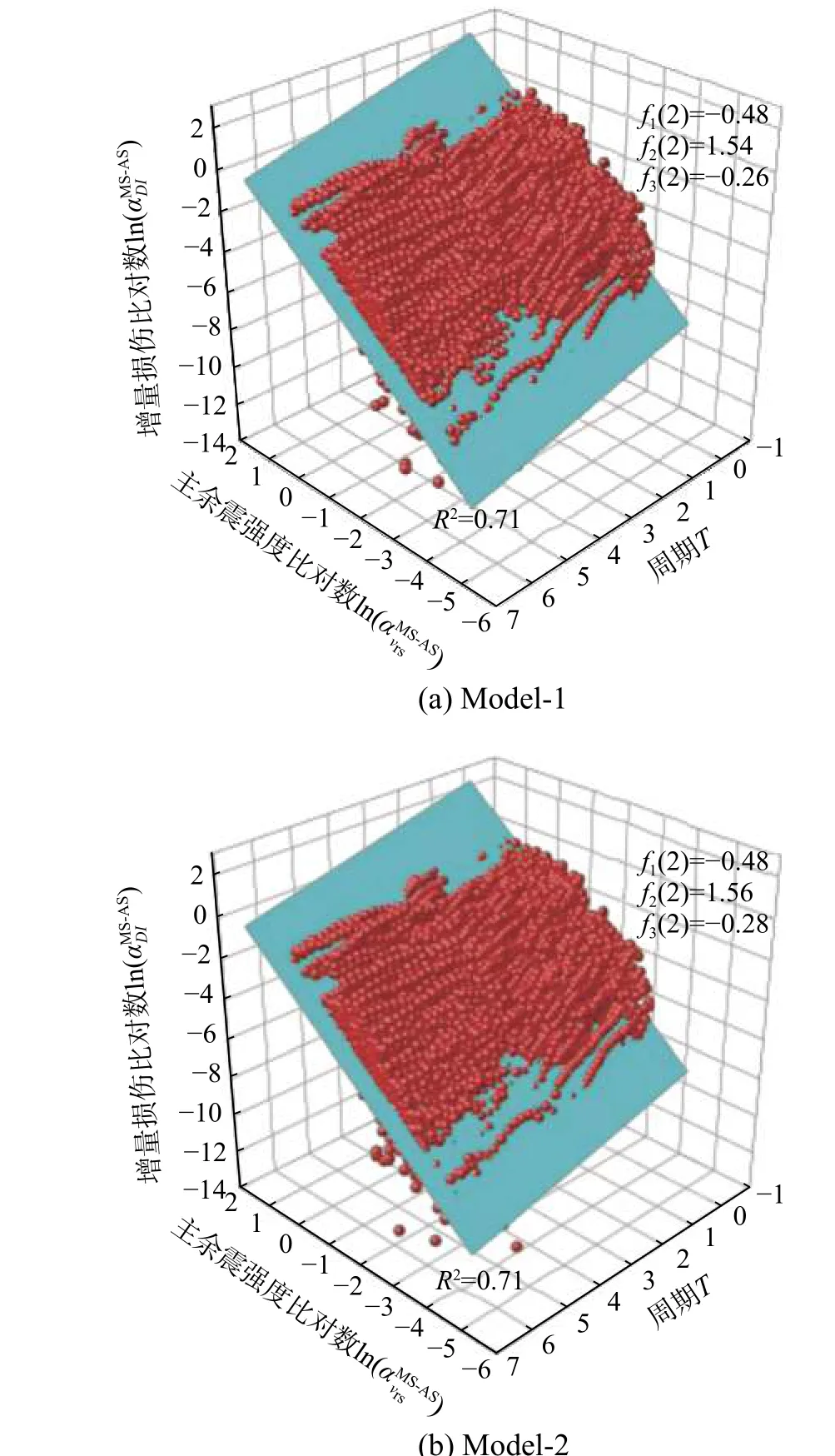
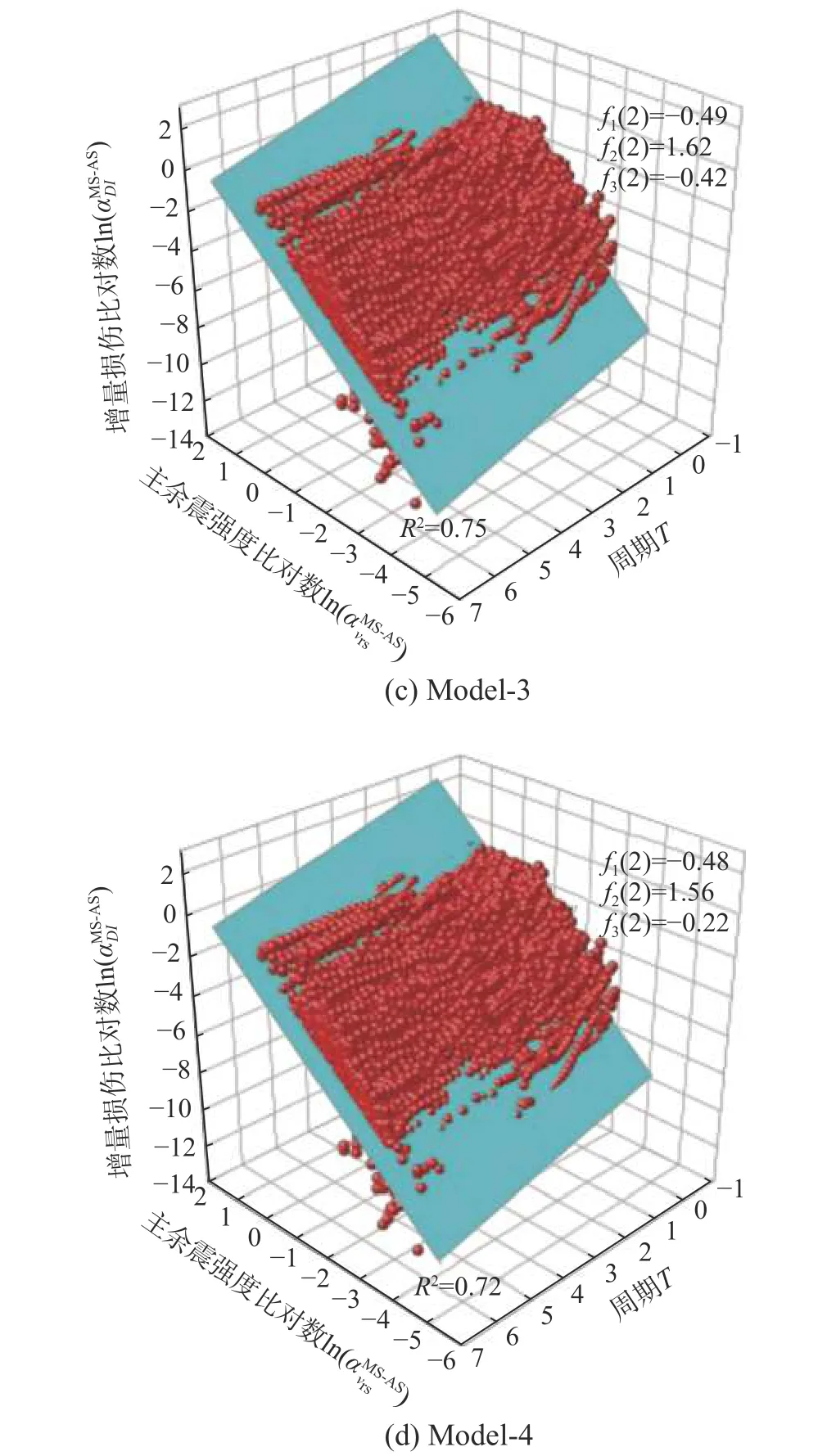
图7 Model-1～Model-4 在Ry =2 时的主余震损伤比预测模型与计算结果Fig. 7 Prediction models and calculated results of Model-1～Model-4 with Ry=2

由表2 可见，f1(Ry)、f2(Ry)和f3(Ry)与Ry具有近似线性关系。因此，采用线性形式对f1(Ry)、f2(Ry)和f3(Ry)进行拟合，如图8 所示。由图可以看出，采用线性模型的f1(Ry)、f2(Ry)和f3(Ry)拟合精 度 较 高。Model-1～Model-4 的f1(Ry)、f2(Ry)和f3(Ry)的拟合结果如表3 所示。

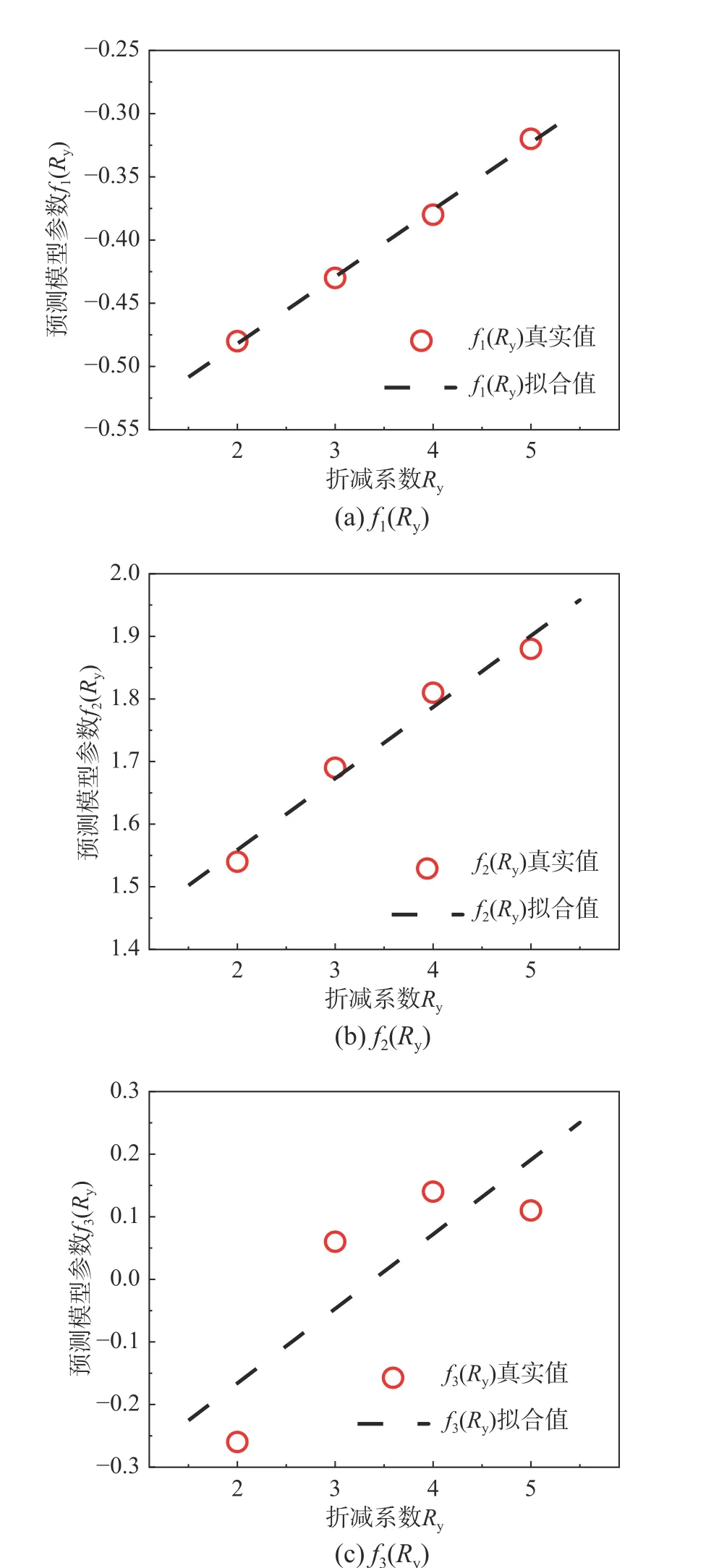
图8 Model-1 中f1(Ry)、f2(Ry)和f3(Ry)的线性拟合结果Fig. 8 Linear regression results of f1(Ry)，f2(Ry) and f3(Ry)

表2 Model-1～Model-4 在不同Ry 条件下的f1(Ry)、f2(Ry)和f3(Ry)的拟合结果Table 2 Regression results of f1(Ry), f2(Ry) and f3(Ry) on the cases of Model-1～Model-4 with various Ry values

表3 f1(Ry)、f2(Ry)和f3(Ry)的线性拟合结果Table 3 Linear regression of f1(Ry)，f2(Ry) and f3(Ry)

5 增量损伤比预测模型的讨论

5.1 预测模型的精度验证

采用预测值与真实值比值的平均值γmean和中位值γmedian来衡量所提出的增量损伤比预测模型精度。γmean和γmedian的值越接近于1，模型的预测精度越高。主余震增量损伤比的真实值与预测模型求解得到的预测值的对比，如图9 所示。

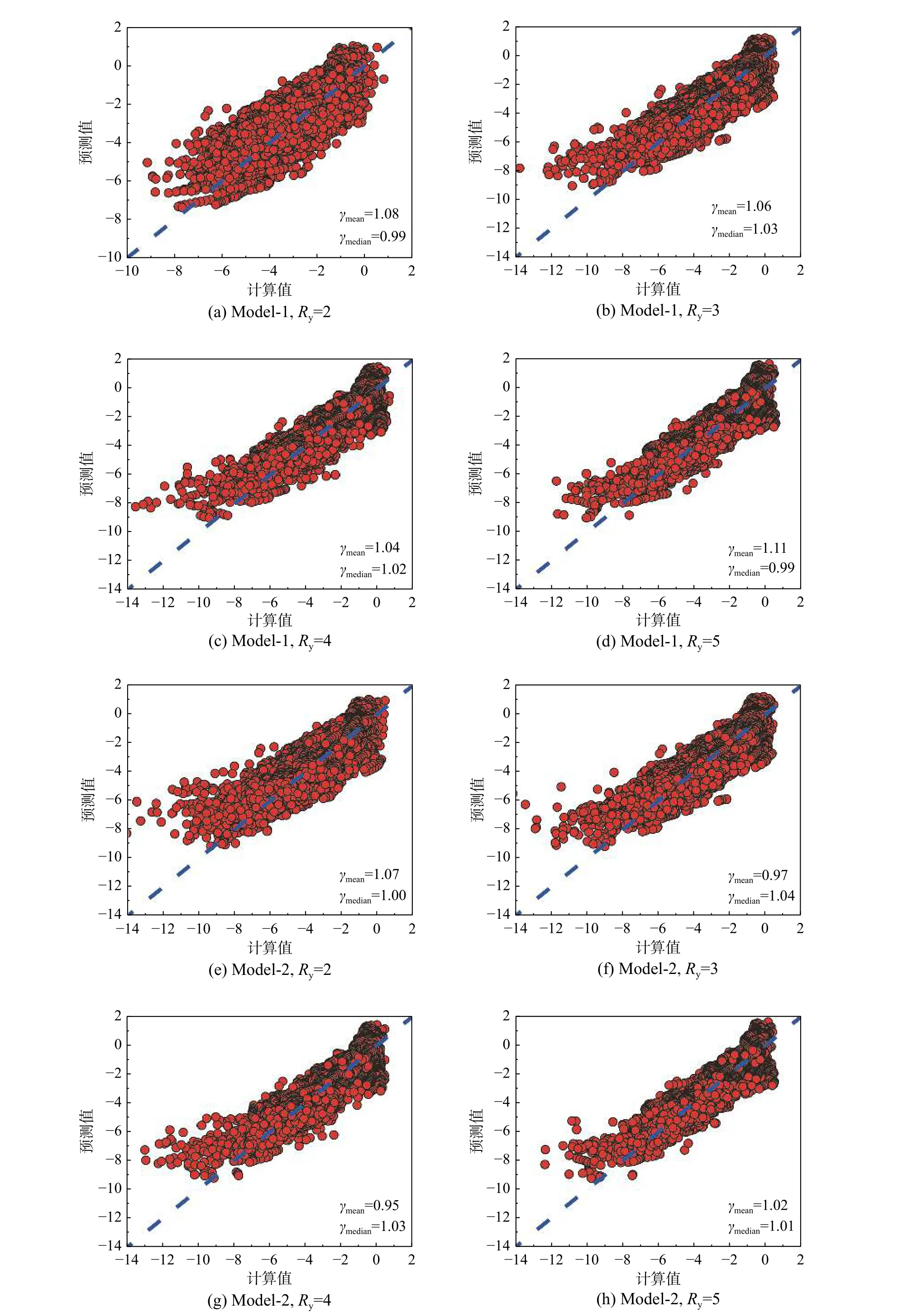
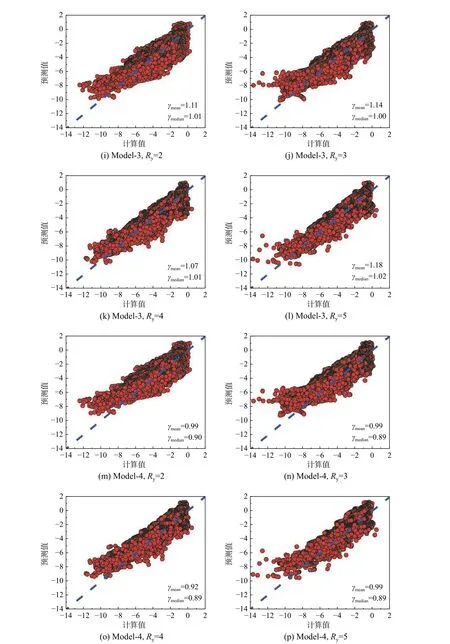
图9 计算值与预测值对比图Fig. 9 Comparison between real data and predicted data

5.2 滞回模型的影响分析

为探究不同的SDOF 滞回模型对余震增量损伤比预测模型的影响，将Model-2、Model-3 和Model-4 的模型结果分别与基础模型Model-1 的模型结果进行对比，并以此来分析P-Δ效应、捏缩效应和强度退化效应对增量损伤比的影响。图10展示了上述不同因素对增量损伤比的影响。由图10可以看出，在这三种滞回模型关键因素中，捏缩效应对增量损伤比的影响最大，其次是强度退化效应。P-Δ效应对增量损伤比的影响非常小。

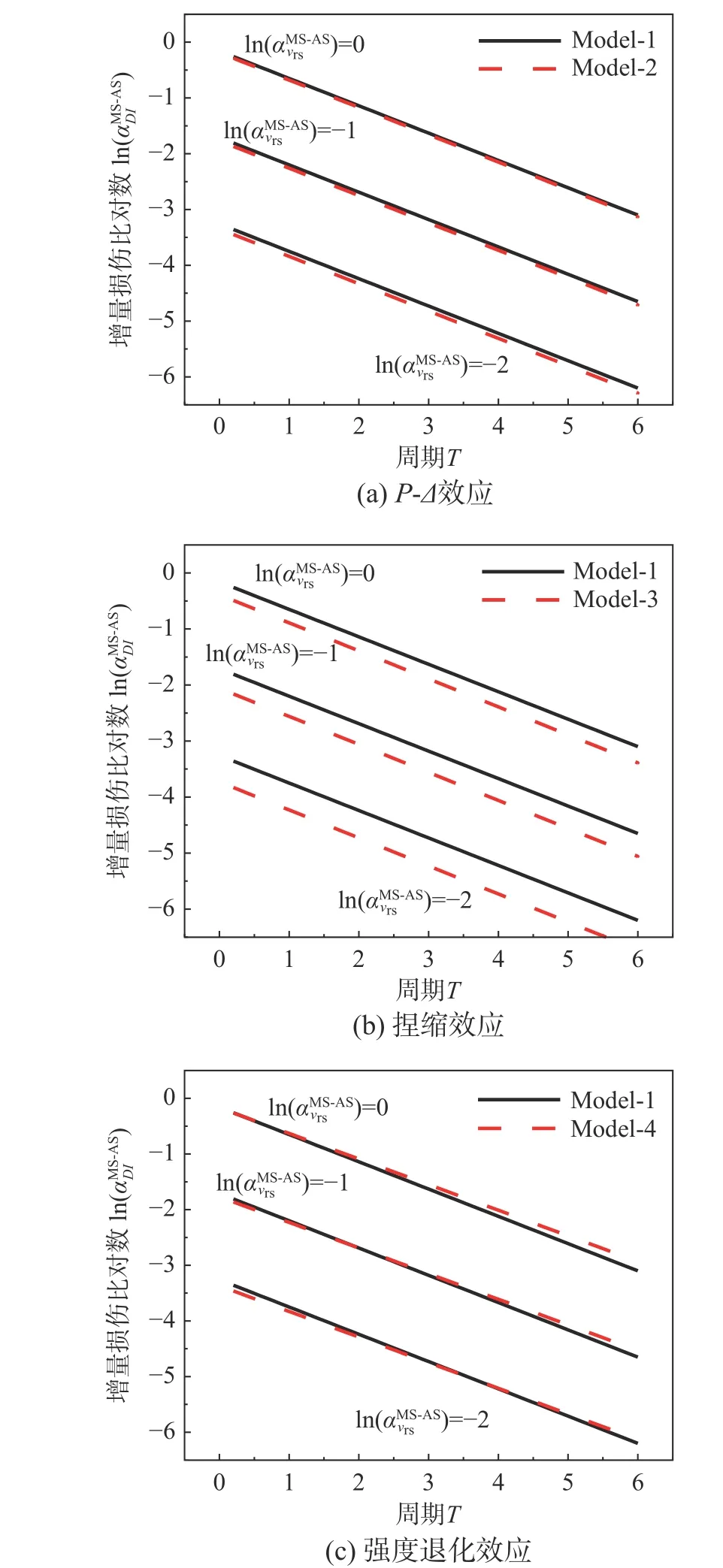
图10 滞回模型关键因素对增量损伤比的影响Fig. 10 Influence of key factors of the considered hysteretic models on incremental damage ratios

折减系数Ry对增量损伤比的影响，如图11所示。由图可见，Ry对增量损伤比的影响较为明显。随着Ry的提高，增量损伤比曲线的坡度降低，说明Ry的提高降低了结构周期对增量损伤比的影响。这主要是因为Ry的提高增强了结构的非线性程度，可使结构更早地进入非线性阶段，结构更易在主震阶段发生屈服，因此降低了由周期不同引起的结构差异性对结构主余震损伤的影响。

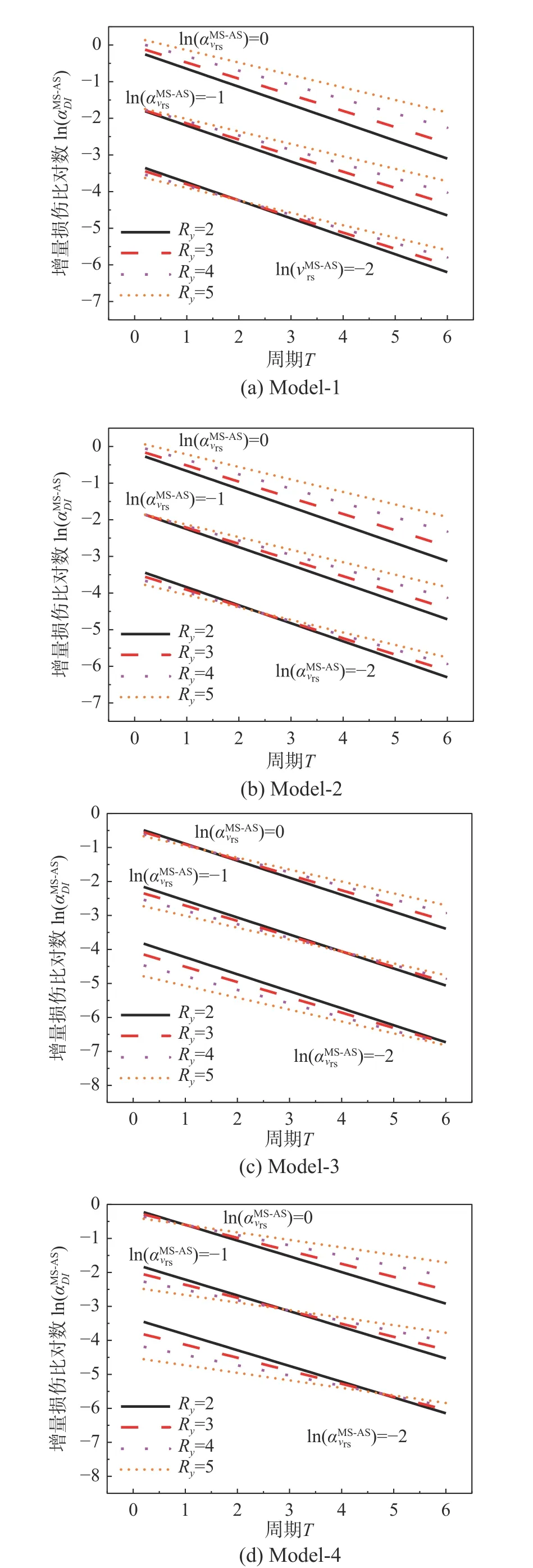
图11 折减系数Ry 对增量损伤比的影响Fig. 11 Influence of Ry on incremental damage ratios

6 结论

本文以一组SDOF 体系为研究对象，以一系列真实主余震序列作为地震输入，采用增量损伤比作为描述参数，对结构的增量损伤开展了全面的研究。给出了增量损伤比的预测模型，并对预测模型的精度和影响因素进行了讨论，主要结论如下：

(1) Park-Ang 损伤指数具有单调递增性，可以较好地克服“极性”问题，便于主震损伤和余震损伤的叠加。以基于Park-Ang 损伤指数的余震增量损伤和主震损伤比值与主余震强度比具有良好的线性相关性。

(2) 本文提出的余震损伤比预测模型具有较高的预测精度，便于量化余震对结构损伤的影响。

(3) 在全周期范围内，对增量损伤比的影响由强到弱的因素依次是：捏缩效应＞强度退化效应＞P-Δ效应。强度折减系数Ry在四个SDOF 计算结果中对增量损伤比均产生了较大的影响。