考虑GIS信息的城市配电系统网格化动态投资策略优化

马杰, 李秋燕，王利利，于昊正，郭新志，唐早，李争博，苏童，刘友波

(1. 国网河南省电力公司经济技术研究院，郑州市 450052；2. 四川大学电气工程学院，成都市 610065)

0 引 言

随着配电网规划技术的不断发展，大量的供电企业开始开展配电网网格化规划的研究和实践[1-2]。配电网规模庞大，采用网格规划的方法主要是为了将庞大的复杂大区域划分成若干相对独立的网格进行简单的网架规划。化整为零后的配电网规划可以避免配网集中规划计算量大的问题。

网格化规划思路[3]主要是针对所规划的大区域，基于其行政属性、地貌属性、负荷分布等方面进行区域配电网格划分，然后对各个网格进行独立规划布线。文献[4]和[5]分别讨论了采用基于负荷密度划分和行政街道划分的配电网网格划分方法，结果表明，上述方法均能实现较好的配电网网格划分。

配电网网格化规划的主要规划思路是，依据城市的功能将所建设区域划分成若干网格[6]。配电网格内部通常有互联的2～4座110 kV变电站，是制定目标网架规划、统筹廊道资源及变电站出线间隔的基本管理单位，本文的规划思路也是围绕配电网的规划展开的。供电网格由若干个供电单元组成，供电单元通常由1～3组馈线互联，是网架分析、线路联络结构确定、规划项目方案编制的基本单元。文献[7]明确了配电网网格及台区单元的划分依据，并从用户侧和企业侧2个角度给出了中低压配电网网格评估指标和指导原则，但并未明确具体的配电网划分方法和规划模型。文献[8]基于网格化思想，以“联络组合”为核心思路，构建模型对已建成地区的网架结构进行线路改造优化，但忽略了即将开发区域的配电网规划问题。文献[9]提出一种确定规划网格目标网架和过渡网架的网格划分思路。文献[10]提出了一种面向可靠性提升的关联规则驱动下的配电网投资优选模型与方法，采用数据驱动的方法，深度挖掘规划方案-评估指标之间的关联关系，避免了传统的复杂物理建模，但其所挖掘的关联关系的准确性和通用性有待进一步提高。无论是传统的网架规划方法，还是上述网格化规划方法，均需基于城市配电网进行具体建模仿真，同时对大区域多网格进行规划，存在不收敛的可能，并且区域内线路耦合严重，增加了线路复杂度以及维护的难度。

综上，考虑到配电网网架、多阶段负荷动态增长特性和配电网地理信息系统(geographic information system, GIS)信息以及新能源资产所在位置，提出更加符合配电网投资与建设的城市配电网网格动态投资策略优化模型。首先，利用OpenDSS平台实现投资策略生成与规划后评价指标校验。其次，明确配电网多阶段投资的多重目标。然后，采用NSGA-Ⅱ寻找当前网格规划背景下的最优投资策略，实现动态投资策略优化求解[11]。最后，利用OpenDSS和Matlab的交互特性，实现所提出模型和算法在OpenDSS/Matlab的跨平台编程，并通过某城市配电网的真实算例验证本文所提出模型和方法的有效性和合理性。

1 考虑GIS信息的配电系统网格化规划

1.1 考虑GIS信息的网格规划原理

网格规划[12]是配电网规划的核心内容之一，在城市配电网规划过程中，配电网网格划分[13-14]的依据有以下4点：

1)考虑市政规划中地块的功能及开发情况，合理选择规划用地；

2)考虑网格区域内部的地形属性，如网格内部是否含有山脉河流等特殊的地形结构；

3)考虑当前电网的建设情况，避免对现有的网架结构进行过度改造；

4)考虑同一个网格内的负荷密度和用户的分布状况，避免出现同一个用户被2个网格切割的情况。

本文根据以上4点将整个配电网络划分为数个网格的小单元。配电网网格划分后，规划难度降低，不同的网格之间相互独立，网格内结构清晰。将网格内部的负荷预测结果、变电站位置等与GIS信息相结合，找到一种遵循电网约束和实际地理约束的可行方案，并通过不断改变馈线分布降低成本和提高网架的承载能力，从而得到一个最优的网架结构。

1.2 多阶段动态规划思路

配电网建设属于循序渐进的，不能一蹴而就。在电网规划时，基于现有网架结构方案与未来该地区的宏观经济发展计划，制定得到该地区的目标网架。配电网从初始网架发展至目标网架属于动态规划的范畴。

图1给出了配电网网格规划多阶段动态示意图。从初始网架出发，逐次筛选出各个阶段的最优规划路径。需要注意得是，第n个阶段的规划是基于第n-1个阶段的规划网架展开分析的。

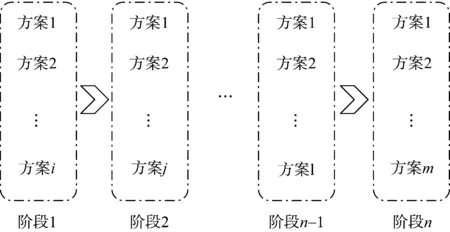
图1 多阶段动态规划示意图Fig.1 Multi-stage dynamic programming

2 配电网多阶段动态规划模型

2.1 目标函数

本文为多阶段动态投资，投资策略不仅要保证配电系统运行安全，并且还要尽量减少投资成本，因此本文考虑以下5个目标。

1)投资成本：

(1)

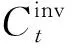
2)线路损耗功率：

(2)

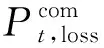
3)平均电压偏差：

(3)

式中：SB是配电系统母线集合；NB为母线总数；Vt,lB是t周期内母线lB的电压标幺值。

4)N-1验证合格率：

(4)

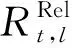
5)配电系统重载率：

(5)

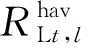
2.2 运行约束

为保证规划方案的安全性与合理性，需保证设备在运行过程中满足如下三方面的约束：系统运行约束、分布式电源运行约束以及网架结构约束。

1)系统运行约束。

配电系统运行约束如下：

(6)

(7)

(8)

(9)

(10)

(11)

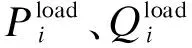
2)分布式电源运行约束。

分布式电源的有功无功出力约束如下：

(12)

(13)

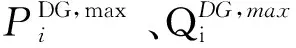
3)网架结构约束。

配电系统须满足辐射状运行，因此须满足如下辐射状约束:

bji+bij=xij,∀j→i∈ε

(14)

(15)

bij=0,∀j∈R,∀i∈Ωj

(16)

式中：bij为线路关系变量，若节点i为j的父节点，则bij=1，否则为0；xij为线路连接关系变量，若节点i和j相连，则xij=1，否则为0;ε、E、R、Ωj分别表示所有可能线路构成的集合、所有节点构成的集合、所有根节点构成的集合、与节点j相连的所有节点构成的集合。

3 基于NSGA-Ⅱ的配电网投资优化

3.1 NSGA-Ⅱ算法流程

本文所提配电系统动态投资模型包含5个目标函数，传统单目标优化算法[15-17]无法适应多目标优化问题[18]。因此本文使用多目标优化算法NSGA-Ⅱ来求解配电系统最优规划方案。NSGA-Ⅱ由NSGA发展而来，比NSGA拥有更高的运算速度和更好的解集收敛性[19]。可以在不可穷举的状态空间内结合配电系统实际约束求出投资的最优解。将NSGA-Ⅱ用于配电网投资的具体流程为：

1)利用第一个规划周期的节点随机生成规模为N的初始规划方案作为初始种群P0，通过突变、交叉和选择得到第1代子种群Q0；

2)将父代种群与子代种群合并，形成一个大小为2N的种群R0，再进行快速非支配排序并且分层；

3)对每个非支配层中的个体进行拥挤度计算，根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群P1；

4)循环第一步的突变、交叉和选择操作得到第2代子代种群Q1，将P1和Q1再次合并形成R1，直到迭代次数达到最大值，从而生成当前投资周期最优投资策略；

5)以前一个规划周期选择的路线为存量电网进行下一个周期最优投资方案的规划，即在存量电网的基础上通过NSGA-Ⅱ算法的基本操作产生新的子代种群；

6)按照第一个投资周期所进行的操作进行重复，直到完成最后一个投资周期的迭代。至此，生成多周期动态最优投资策略。

该算法的流程如图2所示。

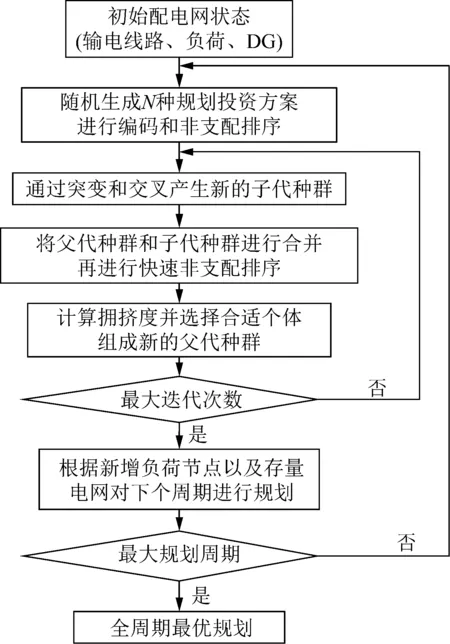
图2 动态投资策略流程Fig.2 Flow chart of dynamic investment strategy

3.2 快速非支配排序和拥挤距离计算

NSGA-Ⅱ算法的核心步骤为快速非支配排序和拥挤度计算。快速非支配排序的关键在于求取Pareto最优解集，NSGA-Ⅱ算法先计算个体的适应度，并根据适应度对个体进行非支配排序，根据排序结果对个体进行分层，使同一层内个体互不支配。之后对同一个非支配层的个体进行拥挤度计算，并利用非支配关系以及个体的拥挤度来选取合适的个体形成新一代种群，最终找到Pareto最优解集。

3.3 投资策略编码、突变与交叉

对配电网规划线路进行编码会出现染色体过大和不可行的情况[20]，为了避免这个问题，使用浮点数编码[21-23]作为染色体的编码方式。如：可将节点i与节点j连接起来的线路编码为i.j。以图3为例，图3中共有9个节点，所以形成开环运行的网络应该含有8条支路。通过随机选取的8条线路组成一种投资方案可以得到一条染色体，并对含8条线路的染色体进行浮点数编码，编码结果为：1.2-2.3-3.4-4.5-5.6-6.7-7.8-8.9。

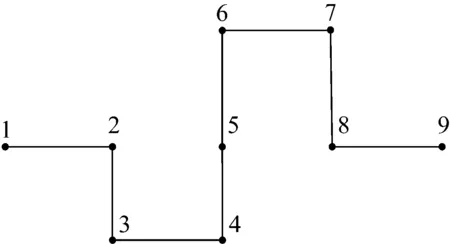
图3 染色体编码Fig.3 Chromosome coding

由于本文编码方式使用的是浮点数编码，所以相应的突变和交叉操作也应该有其对应的规定，方法如下：

1)突变。

与初始种群的形成类似，突变问题同样需要使用对应的方法。在本文中，针对NSGA-Ⅱ的突变问题随机选取一组基因进行突变来改变染色体，以保持多样性且不会改变其辐射状结构。图4为染色体突变示意图，如图4所示，染色体A(1.2-2.3-3.4-3.5-5.6)的第三个基因发生突变，突变为染色体B(1.2-2.3-2.4-3.5 -5.6)。

图4 染色体突变Fig.4 Chromosomal mutation

2)交叉。

交叉问题与突变问题有所不同，需要使用2个染色体进行交叉操作，从而产生2个不相同的子代。图5为染色体交叉示意图，图5中：A(1.2-2.3-3.4-2.5-5.6-6.7-5.8 -8.9)和B(1.2-2.3-2.5-5.4-5.6-5.8-8.7-8.9)通过交叉操作生成子代C(1.2-2.3-3.4-2.5-5.6-5.8-8.7- 8.9)和子代D(1.2-2.3-2.5-5.4-5.6-6.7-5.8-8.9)。

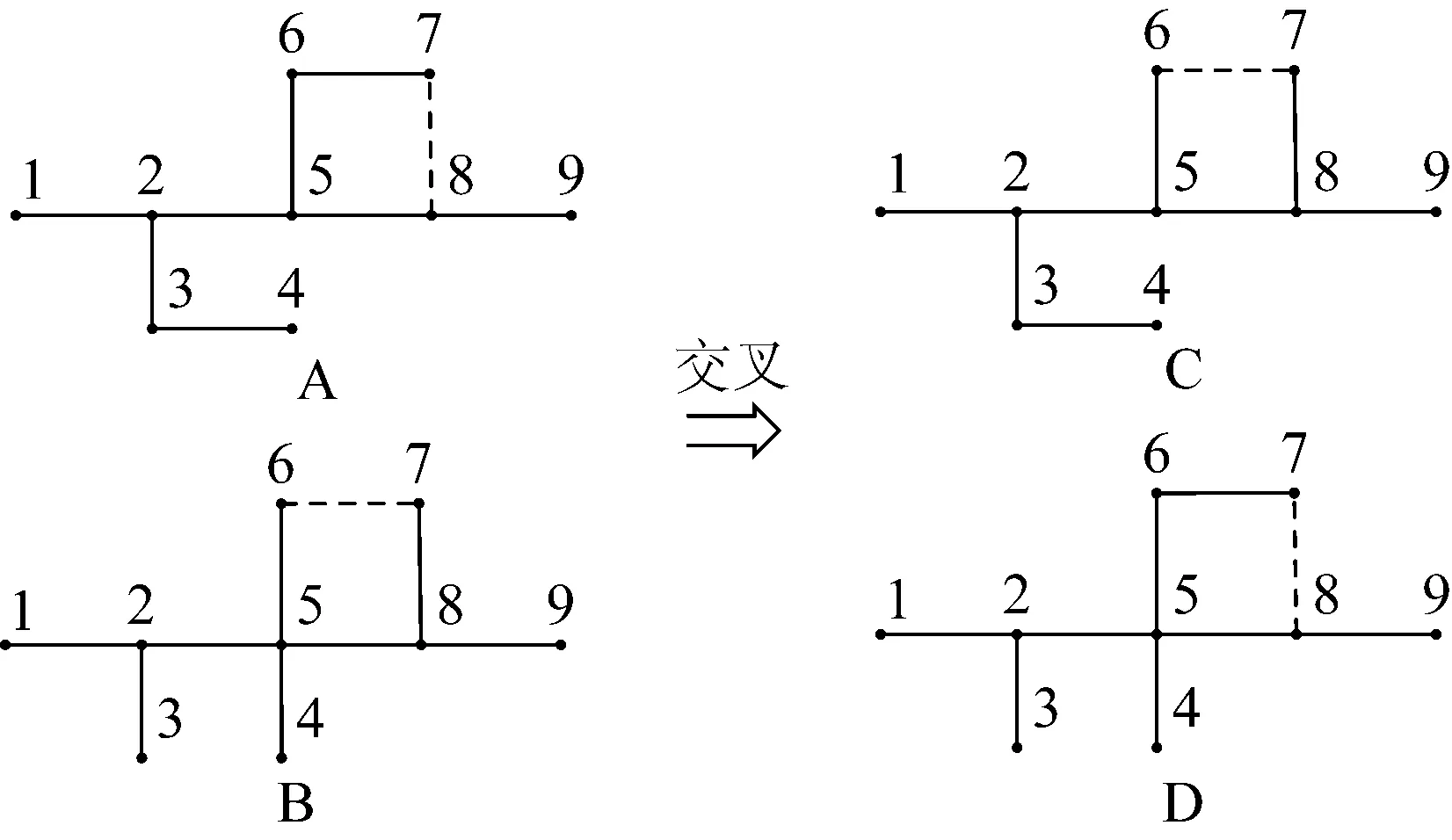
图5 染色体交叉Fig.5 Chromosomal crossing

4 算例分析

对本文所提算法在某城市配电系统上进行网格化投资测试，以证明算法的可行性。对该配电网格进行等效，在OpenDSS上搭建潮流仿真计算模型，并基于OpenDSS和Matlab交互仿真，实现算例分析与验证。

4.1 算例系统介绍

本文选取某个高速发展的城市配电系统展开分析。文献[24]中提到，配电网网格划分原则具有一定的先验性，用于规划的专家意见带有很强的主观性，此外，规划过程中还应以行政区域划分为边界条件，配合市政部门的基础设施建设等，需要满足多个方面的要求。本文基于上述分区要求，采用文献[24]所提的网格化划分原则，对配电网格分区成果图开展规划工作，得到如图6所示的4个配电网格，并开展对配电网格2的动态投资分析。

图6 配电网格划分成果图Fig.6 Grid division result of a distribution network

根据该配电网格区域经济发展情况，未来5年配电网格2的预期投资目标网架及潜在负荷、廊道分布等如图7所示。由于该城市配电系统定义为未来新城市建设核心区域，网格负荷内均为A类负荷，供电区域为A类供电区域。其中节点A—D为110 kV变电站，远景投资目标的配电网包含38个10 kV负荷节点及若干条可行的配电线路，均按配电网格廊道图沿街道分布。结合配电网格内变电站、负荷及廊道分布图，开展考虑GIS信息的配电系统网格化动态投资分析。

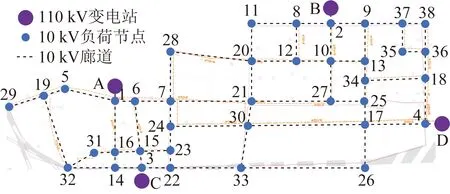
图7 配电网格2内变电站、负荷及廊道分布Fig.7 Distribution map of substations, loads and corridors in the distribution grid 2

该配电系统网格化投资基于以下背景：

1)每年生成20个初始投资方案，投资方案包含新增配电线路选址、导线选型、联络开关选址以及光伏设备选址定容等；

2)每年负荷增长5%～20%；

3)针对A类地区，为进一步提高供电可靠性需求等，所有线路均优先考虑采用电缆线路；

4)设该网格计划5年完成修建任务，每2年基于上一轮周期的网格、网架内已建设设备，结合负荷预测结果，进行配电网投资；

5)投资周期内负荷点的发展情况如图8所示。第1年新增18个负荷点，总有功功率为76.76 MW，总无功功率为38.4 MV·A；第3年新增9个负荷点，总有功功率达到121.44 MW，总无功功率达到60.72 MV·A；第5年新增11个负荷点，总有功功率为166.41 MW，总无功功率为83.2 MV·A。

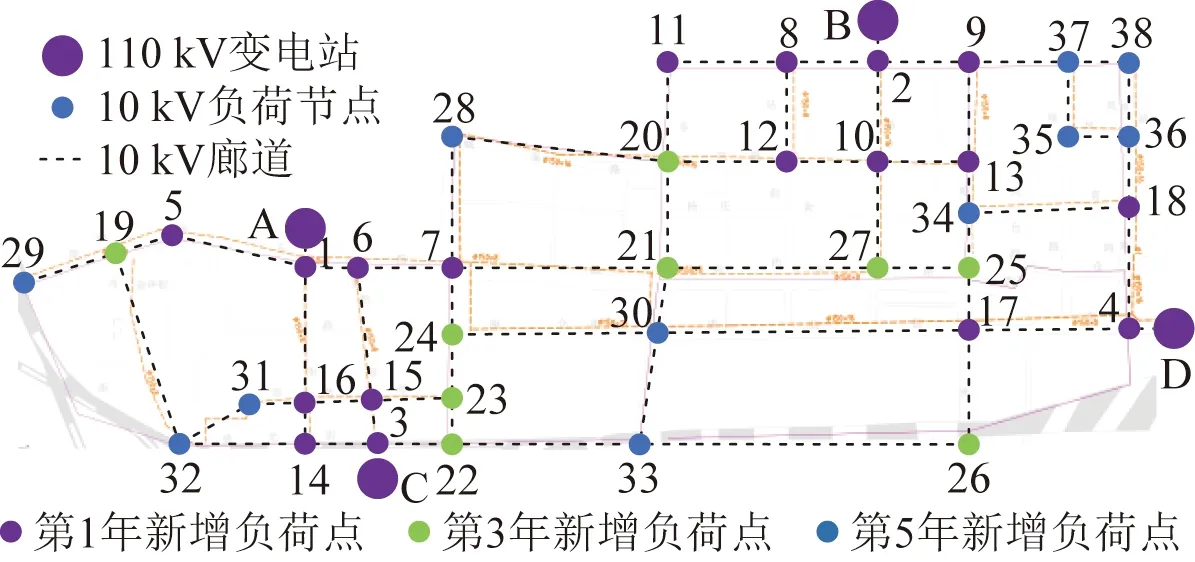
图8 该配电网格5年负荷增长图Fig.8 5-year load growth graph of the distribution grid

4.2 动态投资结果分析

基于算例系统实际情况，经过NSGA-Ⅱ迭代后，可得到Pareto最优前沿[25-26]，其为一系列可行的投资策略，各策略之间互为非支配解，不同的投资策略包含着不同的最优化指标，投资人员可根据投资需求进行选择。本算例中，分别以投资成本、电压偏差和重载率为投资需求，选取了3个具有代表性的投资策略，并展示第5年投资后各评估指标的结果，如表1所示。

从表1可以看出，3个投资策略的N-1校验均为100%，而总有功损耗、电压偏差和重载率都在合适的范围内，故选择成本最低的投资策略3作为本文投资策略，并进行投资结果细节展示，其5年投资方案如图9—13所示。

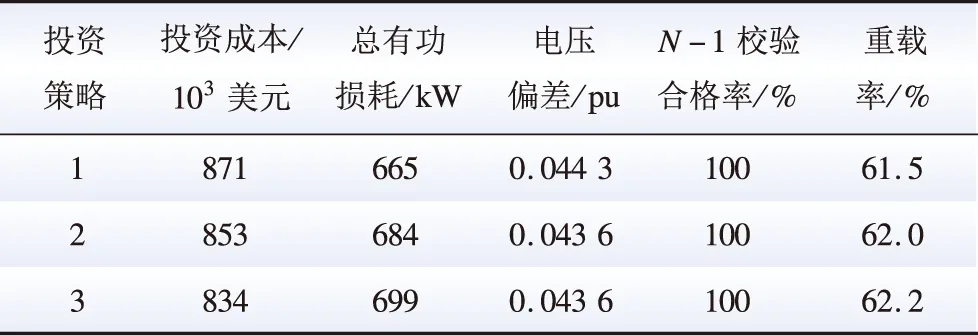
表1 投资策略的Pareto最优前沿Table 1 Pareto optimal front of investment strategies

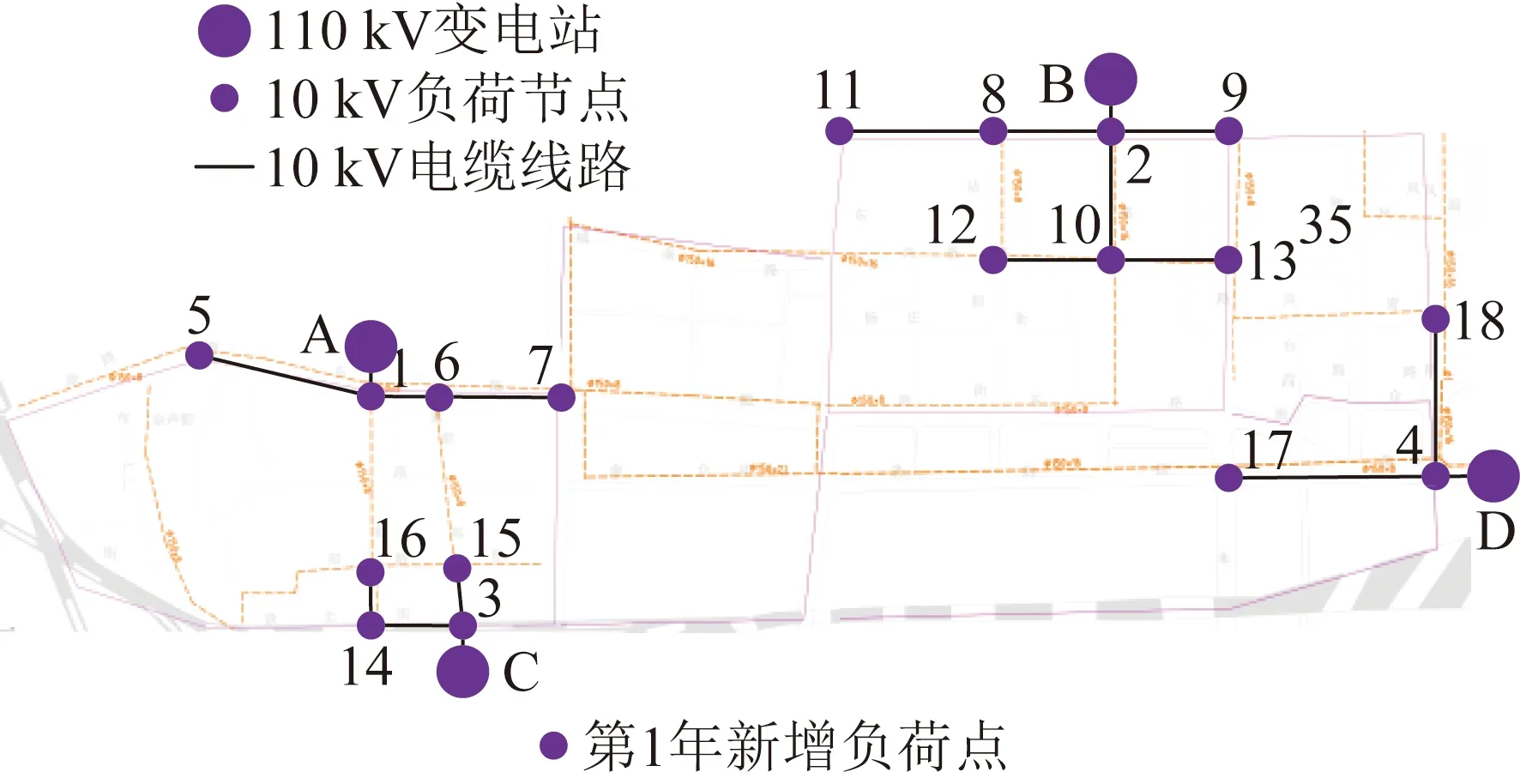
图9 该配电网格第1年投资方案Fig.9 First-year investment in the planning strategy

图9为该配电网格第1年投资方案，以4个变电站为起点，新增配电线路14条，实现了第1年新增负荷节点的供电。图10基于图9投资结果，新增配电线路7条，实现了第3年新增负荷节点的供电。图11基于图10投资结果，新增11条配电线路，连接第5年新增负荷，实现所有负荷节点供电。图12在图11基础上添加联络开关，使该配电网格内所有线路满足N-1检验，并且提升了配电网格内负荷转供能力。最后添加光伏设备，如图13所示，由图13可以看出，光伏均添加在配电网供电末端，保证末端电压稳定，减小供电损耗。对应最终投资方案的各投资指标结果如表2所示。

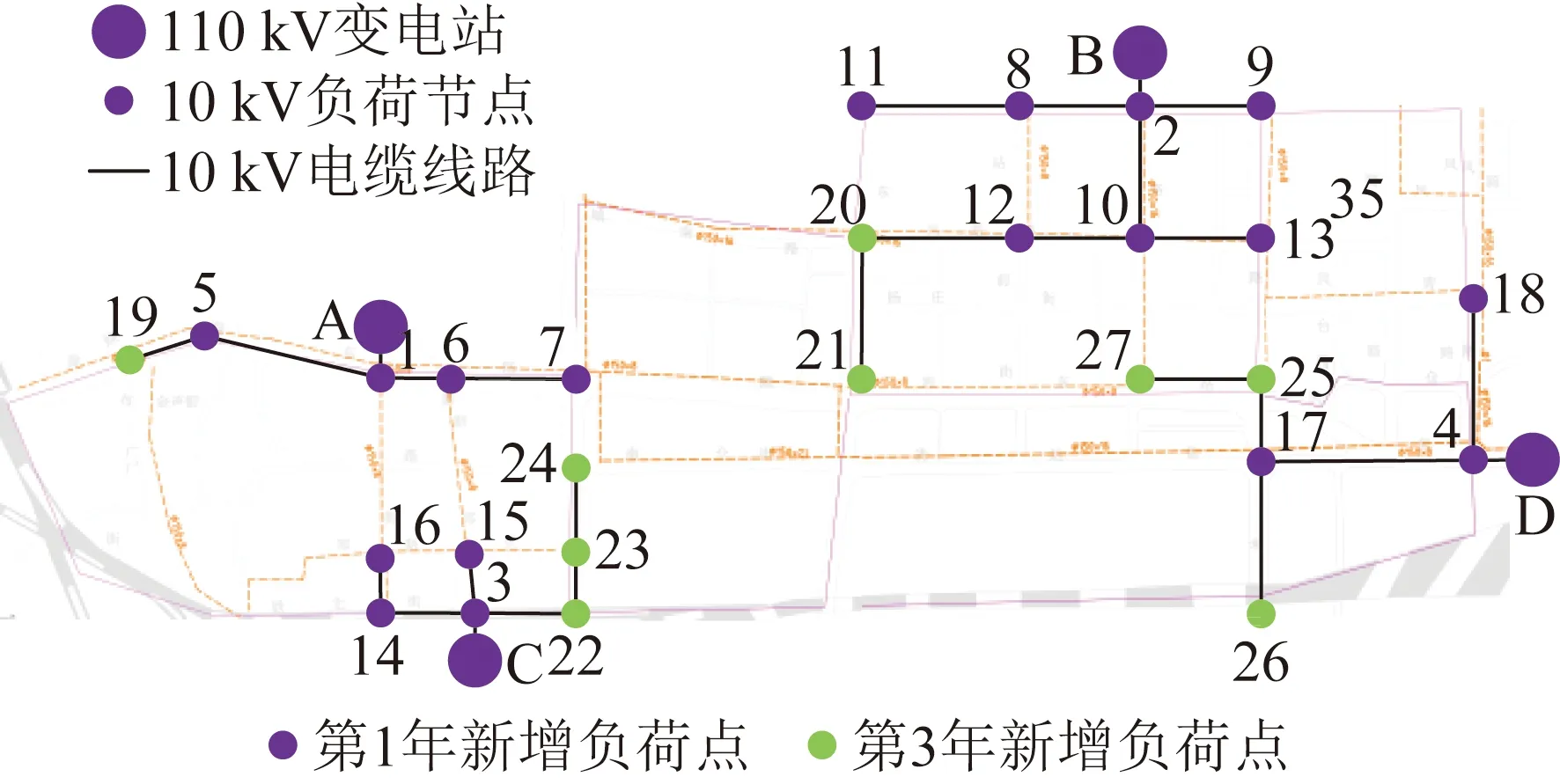
图10 该配电网格第3年投资方案Fig.10 Third-year investment in the planning strategy

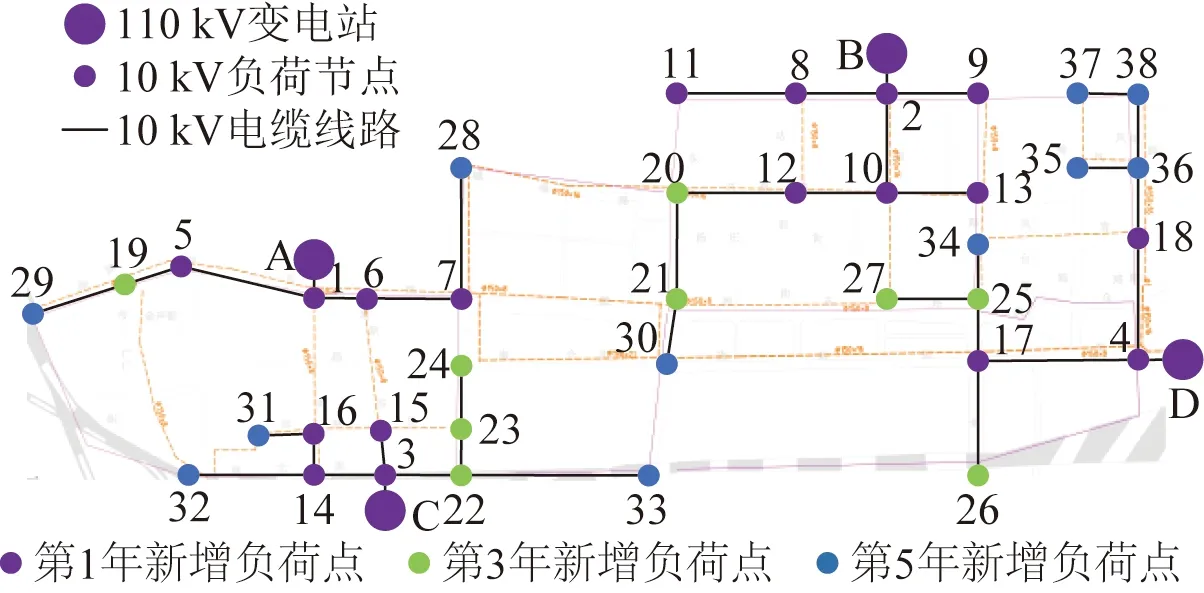
图11 该配电网格第5年投资方案Fig.11 Fifth-year investment in the planning strategy

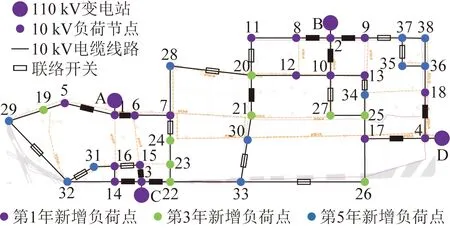
图12 该配电网格添加联络开关后投资方案Fig.12 The planning strategy of the distribution grid after adding interconnection switch

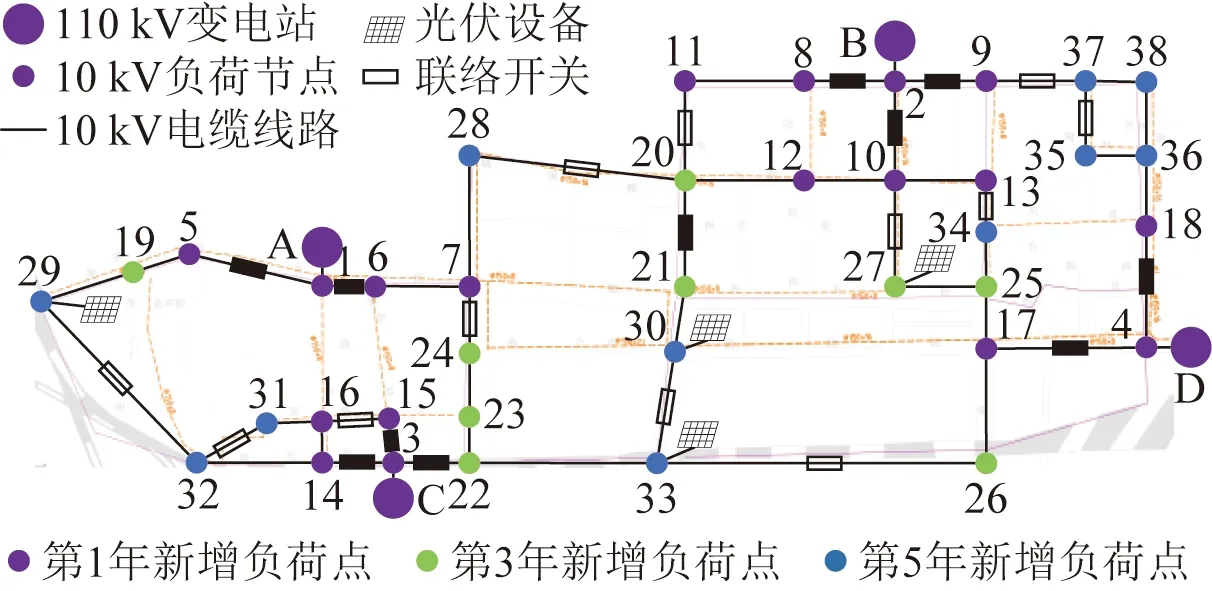
图13 该配电网格添加光伏设备后最终投资方案Fig.13 The final planning strategy after adding PV

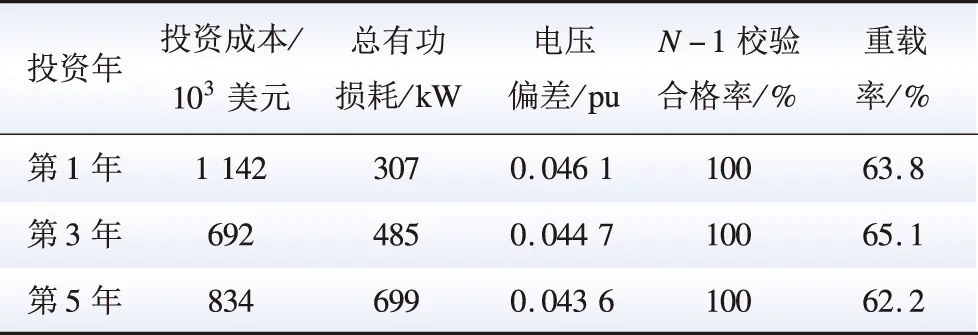
表2 各年最优投资策略下投资指标评估结果Table 2 Evaluation results of investment index under the optimal investment strategy for each year

由表2可以看出，投资成本和配电线路损耗随每年投资策略变化而变化，而电压偏差、N-1校验合格率和重载率均保持在安全运行范围内，表明所生成投资策略可行。根据最终投资方案潮流结果，绘制潮流示意图，如图14所示，图中，黑圈代表变电站，蓝圈代表负荷节点，红线为配电线路，红线越粗则潮流越大。

由于该配电网格为A类供电区，故所有线路均采用双环网结构。由图14可知，线路潮流分布与节点负荷大小、节点位置、配电线路投资方案有关，故根据潮流结果确定电缆回数，设所选电缆线路的截面积为300 mm2，则各电缆线路回数最终结果如表3所示。

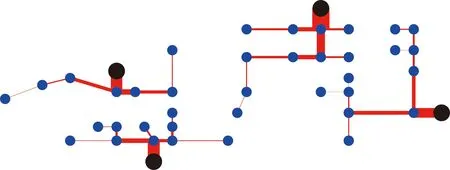
图14 线路潮流大小示意图Fig.14 Schematic diagram of power flow

从表3可以看出，第1年新建配电线路回数较多，其均为主干线路，对后续年份新增负荷起支撑作用，第5年新建线路回数较少，其大多在配电系统末端，潮流较小。表3结果表明投资方案符合实际负荷增长特性。

表3 各电缆线路回数Table 3 Number of each cable lines

最后，本文对比了所提方法和传统(混合整数规划)投资策略的投资结果，如表4所示。

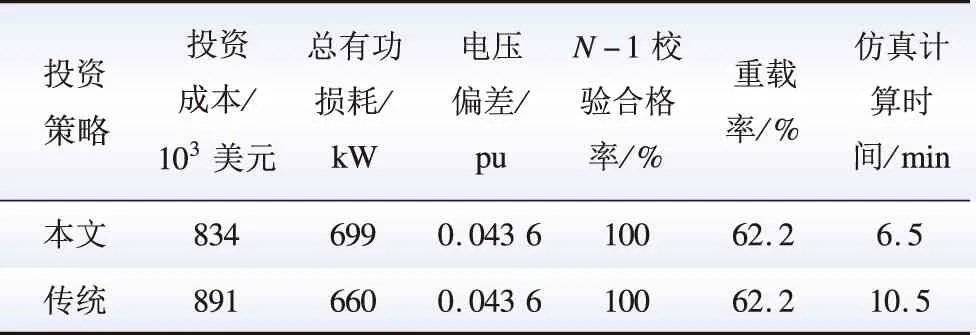
表4 本文方法与传统投资策略对比Table 4 Comparison of the proposed method and traditional investment method

从表4可以看出，本文方法在多个投资指标方面均等于或者优于传统方法，更符合实际应用的需求，此外，求解时间更短，提高了规划效率。而传统方法的求解难度会随着维度规模的增加呈指数增长。本文利用NSGA-Ⅱ算法避免了数学规划方法的“维数灾”，提高了求解效率，此外，在面对未来不确定因素时，可以通过多阶段动态规划灵活调整投资策略，具有更强的适应性能。

5 结 论

本文基于Matlab-OpenDSS配电网投资仿真方法和NSGA-Ⅱ，提出了一种考虑GIS信息的城市配电网格动态投资策略。通过算例分析，得到以下结论：

1)基于Matlab-OpenDSS配电网投资仿真方法可以实现投资方案快速生成与精准校验，并可计算投资策略指标值，是本文方法的基础。

2)基于NSGA-Ⅱ的配电网格投资方法，提高了网格规划效率，可以基于投资策略指标值，对策略进行循环迭代，找到最优的投资策略，并可设置多个投资周期，实现投资策略多周期动态生成。

3)考虑网格划分和GIS信息的配电系统动态投资策略更符合实际应用需求，更符合当前配电网投资背景与实际地理信息，具有实用价值。

4)多阶段动态规划策略提高了配电网实际投资与建设流程的经济效益，且在动态规划过程中考虑了新能源设备的投资，符合未来新能源发展的趋势。