面向区域综合能源系统的分布式优化调度方法

林威，靳小龙，叶荣

(1．国网福建省电力有限公司经济技术研究院，福州市350012；2．智能电网教育部重点实验室(天津大学)，天津市 300072)

0 引 言

随着环境污染的不断加重和能源供给矛盾的日益突出，如何实现能源生产、传输、分配和消费全环节的资源优化配置成为了全世界关注的焦点[1]。通过有效整合现有能源系统的基础设施，打破不同能源系统间分立运行的现状，构建区域综合能源系统(integrated community energy system, ICES)[2]成为了实现区域层面能源供给清洁低碳、能源传输安全经济、能源消费绿色高效的重要手段之一[3-4]。

已有文献对ICES的优化运行和协调互动开展了大量研究。文献[5]提出了能源集线器(energy hub, EH)模型，并基于此研究了综合能源系统经济调度问题。文献[6]研究了热电联产(combined heat and power, CHP)机组不同运行模式对ICES多能潮流计算的影响。文献[7]基于配电系统重构能力，研究了拓扑重构在降低ICES运行成本、提高供电能力方面的潜力。文献[8]考虑ICES运行安全性、经济性及环保性，提出一种多目标优化调度方法，实现ICES多维度能量管理目标。上述文献提出了诸多适用于ICES的优化调度方法，但这些方法均是基于集中式的优化方法[9]，即需要将ICES中涉及的所有运行参数信息上传到统一调度中心进行集中式优化。考虑到不同能源系统通常由不同主体负责运营，如配电系统由配电系统运营商(distribution system operator, DSO)管理并运营[9]，出于信息安全及隐私保护等方面的考虑，不同主体间信息的充分交互共享存在一定困难，对集中式优化调度方法提出挑战。此外，文献[10]指出：随着系统规模的不断增大，集中式优化算法的求解效率有所下降，无法完全适应ICES中多种能源系统耦合接入的需求。

为满足多元主体接入需求，兼顾不同运行主体利益，部分学者提出了采用分布式优化的方法。分布式优化的主要思想是将原本复杂的问题解耦为多个子问题，并独立求解各个子问题，从而达到节省算力、提高计算效率的目的[9]。文献[11]基于交替乘子算法(alternating direction method of multipliers, ADMM)提出了面向电力系统与天然气系统的协调运行方法。文献[12]提出了一种分布式潮流计算方法，从而减轻电力-天然气联合系统间的通信开销。文献[13]研究了电力系统与天然气系统的协调互动。上述文献的研究对象多为以电力-天然气耦合为代表的跨区级综合能源系统，电力系统与天然气系统的耦合多通过燃气机组实现；但ICES中涉及的能源系统更加多样，转换设备亦更加多元，能源耦合关系更加复杂，需要研究面向ICES的分布式优化调度方法。此外，上述文献中主要采用传统ADMM算法，根据跨区级综合能源系统特点将原优化问题拆分为电力系统优化与天然气系统优化两个子优化问题；但ICES中涉及的能源系统更加多样，对应的运营主体亦更加多元，分布式优化需要根据不同主体特点进一步对原问题进行拆分。而传统ADMM算法通常仅能拆分成两个子问题，无法根据主体数量灵活拆分。

为解决上述问题，本文提出一种面向ICES的分布式优化调度方法。首先，分别建立配电系统与配气系统的线性化模型，基于EH概念构建ICES中不同能源间的耦合关系，并引入状态变量进一步优化耦合系统模型。其次，在传统ADMM算法基础上，引入共识变量(consensus variable)用于表征不同能源系统间复杂耦合关系的匹配情况，提出考虑共识变量的ADMM算法(C-ADMM)。进而构建适用于ICES的分布式优化调度框架，实现求解过程根据不同运行主体灵活拆分，满足系统运行成本最优及不同能源系统运行参数保密的要求。最后，采用一个ICES测试算例对本文所提方法进行仿真验证。

1 ICES数学模型

本文考虑的ICES由3个能源系统构成，包括配电系统、配气系统及耦合系统，其中耦合系统实现电力与天然气的能源耦合，并满足终端用户多种类型的负荷需求。

1.1 配电系统数学模型

本文基于Distflow模型[14]对配电系统建模。结合图1所示的配电系统模型，构建线路有功潮流、无功潮流及压降方程，如式(1)—(3)所示：

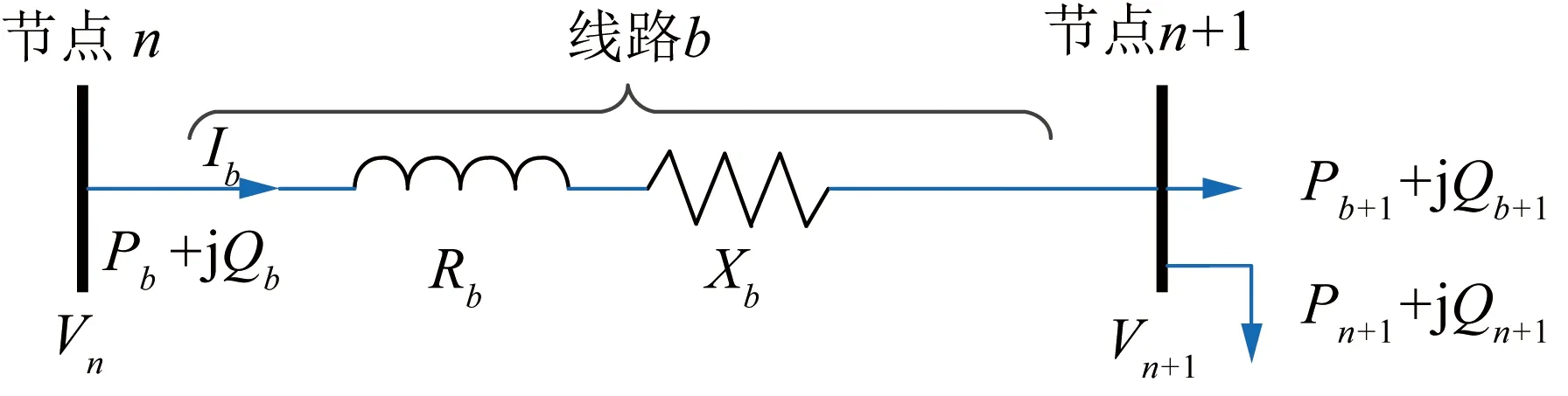
图1 配电系统模型结构Fig.1 Structure of electric distribution system

(1)

(2)

(3)

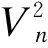
此外，配电系统运行约束条件包括节点电压约束、线路电流约束及系统购电约束，如式(4)—(6)所示：

(4)

(5)

(6)

1.2 配气系统数学模型

配气系统中管道稳态流量方程通常采用Weymouth方程描述[15]，如式(7)所示：

(7)

式中：pl为配气系统管道编号；m为配气系统节点编号；Fpl为管道天然气流量；s(·)为符号函数；kpl为管道流体参数；pm为节点气压。

考虑到式(7)中等式两侧显含变量Fpl，无法直接求解。为此，对式(7)采用如下数学变换：等式两侧同时取平方，并将含Fpl的项移动到等式一侧，如式(8)所示：

(8)

与式(7)相比，式(8)右侧变量在数学上意义更加清晰，即二次函数与符号函数叠加，其图像如图2所示。

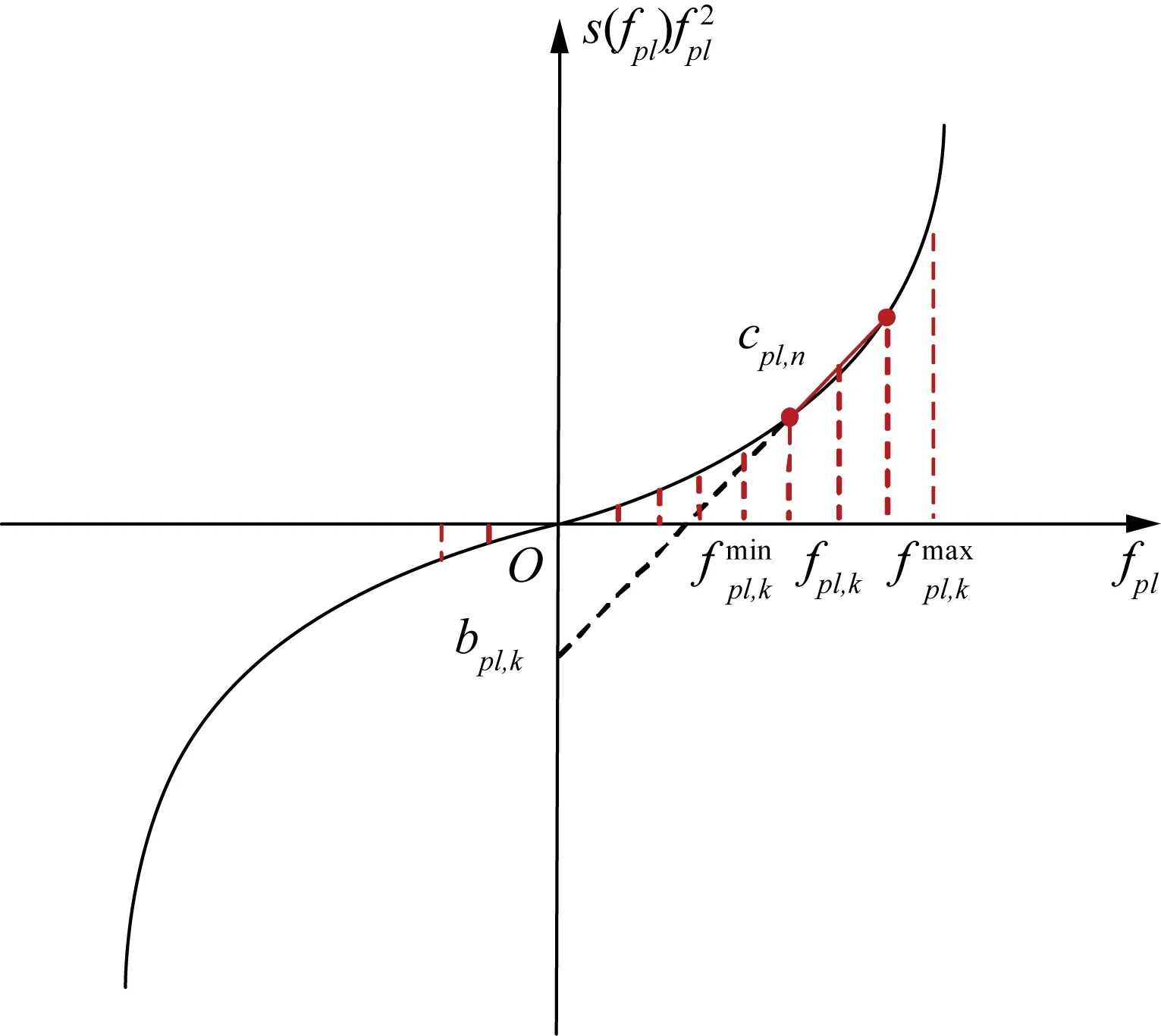
图2 修正Weymouth方程分段线性化Fig.2 Piecewise linearization of modified Weymouth equation

为降低二次项造成的非线性影响，本文采用分段线性模拟式(8)右侧变量[16]，即将式(8)右侧变量拆解为多个分段，每个分段内采用线性函数作近似处理，如式(9)所示：

(9)

式中：k为线性模拟分段编号；N为线性模拟分段总数；cpl,k为线性分段斜率；fpl,k为线性分段取值；bpl,k为线性分段截距；δpl,k为线性分段状态变量。

(10)

(11)

(12)

(13)

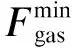
1.3 耦合系统数学模型

耦合系统是实现多元能源网络交互的核心环节，同时也是满足终端用户多类型用能需求的主要途径。耦合系统中涉及了多种的能量转换设备，如电力变压器、CHP机组、中央空调(central air conditioning, CAC)、燃气锅炉(gas boiler, GB)等。通过优化调节设备的运行方式，可灵活满足电、热等不同类型负荷。本文基于EH模型[5]构建耦合系统模型，并以图3所示的两类耦合系统[17]为例，构建能量耦合矩阵。

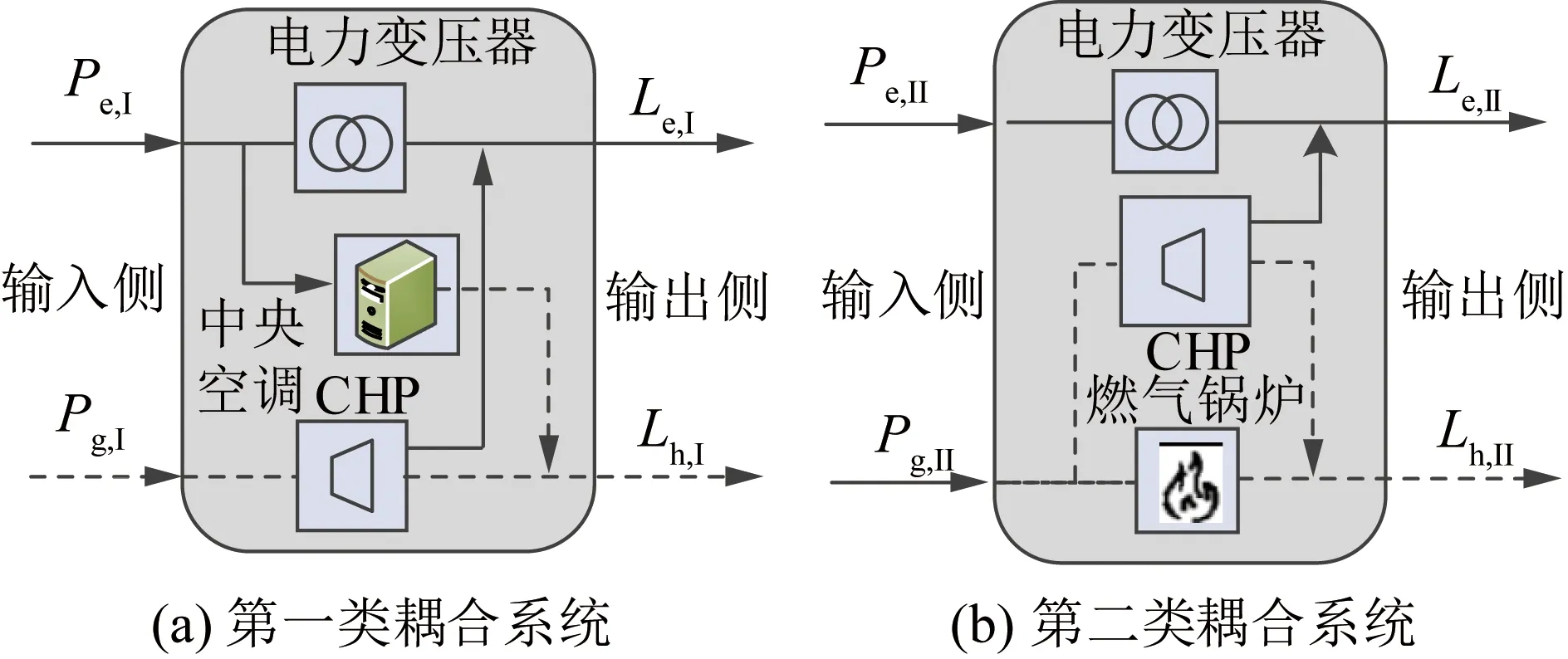
图3 两类耦合系统结构Fig.3 Structure of two types of coupling systems

第一类耦合系统涉及电力变压器、CAC及CHP机组，其能量耦合矩阵如式(14)所示：

(14)

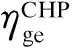
由于矩阵C中引入了分配系数vI，式(14)为非线性。为降低非线性对求解的影响，本文基于状态变量修正能量耦合矩阵，即将矩阵中含vI的元素用状态变量修正，从而使矩阵C转化为线性常数矩阵。结合图3可知：vIPe,I代表中央空调输入侧电功率，将其用状态变量SCAC代换后，式(14)可改写为如式(15)所示的形式：

(15)

第二类耦合系统涉及电力变压器、GB及CHP机组，其能量耦合矩阵如式(16)所示：

(16)

式中：Le,II与Lh,II分别为第二类耦合系统输出侧电负荷与热负荷；Pe,II与Pg,II分别为第二类耦合系统输入侧电功率与气功率；ηGB为燃气锅炉效率；vII为第二类耦合系统的分配系数。

仿照上述转换过程，在式(16)中将CHP机组输入侧电功率vIIPe,II代换为状态变量SCHP，式(16)可改写为式(17)所示的形式：

(17)

考虑到不同能量转换设备的容量限制，两类耦合系统输入侧功率存在对应的上下限约束，如式(18)—(19)所示：

(18)

(19)

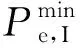
2 分布式优化调度方法

2.1 调度模型

本文考虑的优化调度目标函数为ICES的运行成本，包括购电成本与购气成本两部分，如式(20)所示：

(20)

式中：T为优化调度时段总数；Celec,t为t时段内电价；Cgas,t为t时段内气价。

本文考虑的优化调度约束条件包括各子系统的运行约束，即配电系统运行约束(如式(1)—(6)所示)、配气系统运行约束(如式(8)—(13)所示)及耦合系统运行约束(如式(15)、(17)—(19)所示)。前述章节已对约束条件作详细介绍，此处不再赘述。

2.2 考虑共识变量的ADMM算法(C-ADMM)

传统ADMM算法通常是将目标函数拆分为2个子问题，如文献[11-13]中将综合能源系统的优化调度拆分为电力系统优化问题和天然气系统优化问题。考虑到ICES中还涉及了包含多种能量转换设备的耦合系统，且以配电系统、配气系统、耦合系统为代表的能源系统通常由不同主体运营，多元能源主体接入ICES后其所关注的利益目标可能存在一定差异，传统ADMM算法无法直接应用于涉及多元主体接入条件下的分布式优化问题。

为适应ICES中运行主体多元化、利益目标差异化，本文采用考虑共识变量的ADMM算法进行分布式优化，实现考虑配电系统、配气系统、耦合系统等不同能源主体接入后ICES优化问题的分布式解耦。共识变量是指分布式优化中不同子优化问题间存在耦合关系的变量。以图4所示的ICES模型为例，配电系统与配气系统间的交互是通过耦合系统实现的，耦合系统输入侧电/气功率亦作为配电/气系统输出侧负荷。本文考虑在上述关系中引入共识变量，并使耦合系统输入侧电/气功率、配电/气系统输出侧负荷与共识变量严格相等，如式(21)所示。

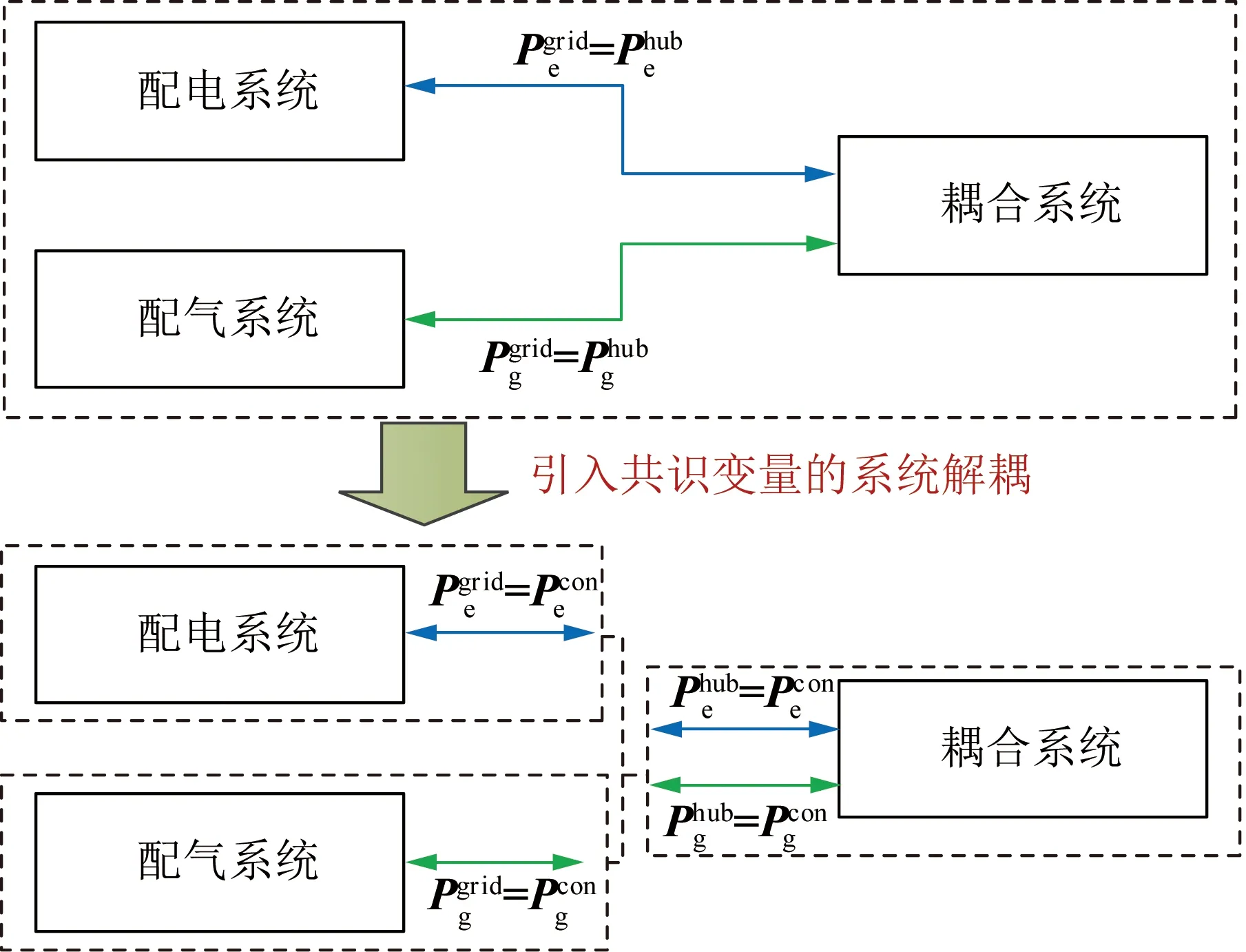
图4 引入共识变量的ICES解耦Fig.4 ICES decoupling by introducing the consensus variables

(21)

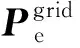
在此基础上，即可将ICES拆分为配电系统、配气系统及耦合系统3部分子系统，并解耦各子系统间的耦合关系，其中耦合系统根据耦合数量进一步拆分后，即可将原有集中式优化问题依照考虑的能源主体数量拆分成对应数量的子优化问题，如在本文算例分析部分将原模型拆分成6个子优化问题(即1个配电系统子优化问题、1个配气系统子优化问题、4个耦合系统子优化问题)，实现多元主体接入后ICES优化调度的分布式求解。

在式(20)中引入共识变量，分别对各子系统构建增广拉格朗日函数，如式(22)—(24)所示：

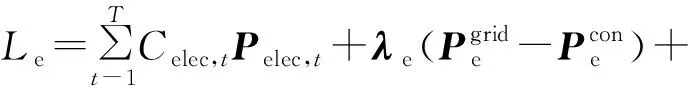
(22)

(23)

(24)

式中：Le为配电系统的增广拉格朗日函数；Lg为配气系统的增广拉格朗日函数；Lhub为耦合系统的增广拉格朗日函数；λe为配电系统的拉格朗日乘子矩阵；λg为配气系统的拉格朗日乘子矩阵；λhub为耦合系统的拉格朗日乘子矩阵；ρ为增广拉格朗日函数步长。

基于前述引入共识变量及构建增广拉格朗日函数的过程，ICES的优化调度问题被拆分成配电系统优化调度、配气系统优化调度及耦合系统优化调度3部分，各子系统调度可在系统内独立并行优化，从而实现集中式向分布式的转变。

在子系统优化过程中，将共识变量及拉格朗日乘子视为常量，从而忽略其他子系统对优化的影响；待各子系统完成优化后，基于各子系统最新的优化结果更新共识变量、拉格朗日乘子，如式(25)—(26)所示：

(25)

(26)

式中：上标q表示迭代次数；Ne为与电功率共识变量相关的配电系统节点数量；Ng为与气功率共识变量相关的配气系统节点数量；Nhub为与电/气功率共识变量相关的耦合系统节点数量。

由式(25)—(26)可见：共识变量及拉格朗日乘子仅需根据各系统耦合变量的最新结果进行更新，无需交换系统的全部运行参数，因此信息传输的时间开销及信息交换的通信开销较集中式优化均大幅减少。C-ADMM算法的收敛条件为原始残差与对偶残差同时满足收敛误差，如式(27)—(28)所示：

(27)

(28)

式中：r(q+1)为第q+1次迭代对应的原始残差；εpri为原始残差的收敛误差；s(q+1)为第q+1次迭代对应的对偶残差；εdual为对偶残差的收敛误差。

2.3 分布式优化模型求解

本文结合C-ADMM算法，解耦ICES优化问题，实现优化调度的分布式求解。以t时段为例，模型求解具体过程如下：

1) 读取t时段内的系统数据，分别对配电系统、配气系统及耦合系统进行初始化；设置初始共识变量、拉格朗日乘子，并令迭代次数q=1。

2) 解耦ICES优化调度模型，分别构建配电系统、配气系统及耦合系统的优化调度模型；将共识变量、拉格朗日乘子视为定值，并行优化各子系统目标函数。

3) 基于各子系统优化结果，更新共识变量及拉格朗日乘子，并计算原始残差及对偶残差。若原始残差及对偶残差同时小于收敛误差，则输出优化结果；否则，令q=q+1，返回步骤2)。

前述章节已建立各子系统的数学模型，在解耦ICES优化调度模型后，各子系统可并行优化。本文构建的分布式优化求解框架在MATLAB平台开发实现，各子系统并行优化过程基于Yalmip软件包[18]编程，并调用CPLEX[19]进行求解，分布式优化求解流程如图5所示。

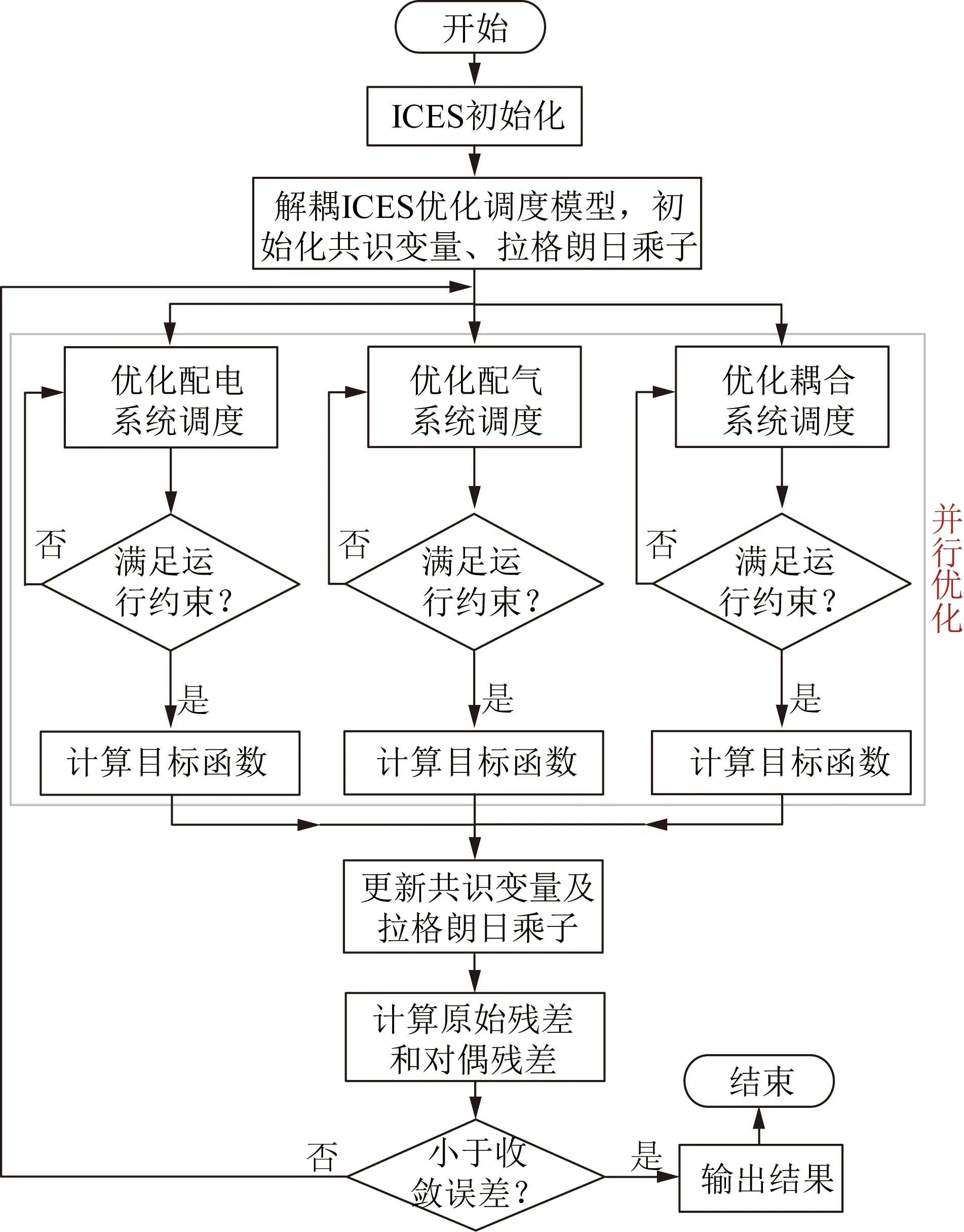
图5 分布式优化调度流程框图Fig.5 Flowchart of decentralized optimal scheduling

3 算例分析

3.1 算例描述

采用图6所示的ICES算例对本文所提方法进行验证，并假设配电系统、配气系统及耦合系统均由不同主体运营，算例中共涉及6个能源主体。其中，配电系统基于IEEE 33算例，系统数据参考文献[20]；配气系统基于14节点配气系统算例，系统数据参考文献[21]；耦合系统包括4个EH，其中EH1与EH3为第一类耦合系统，EH2与EH4为第二类耦合系统。配电系统节点电压的上下限分别设为1.05 pu与0.95 pu。配气系统节点压力的上下限参考文献[21]。耦合系统电/热负荷在文献[22]基础上适当修正，如表1所示。设备运行参数及能源价格参考文献[17]。

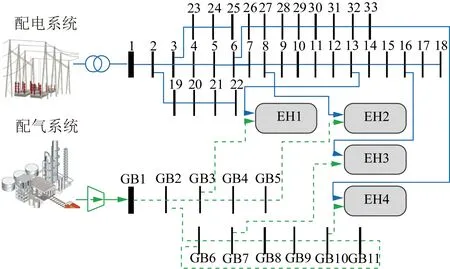
图6 ICES算例结构Fig.6 Structure of the ICES

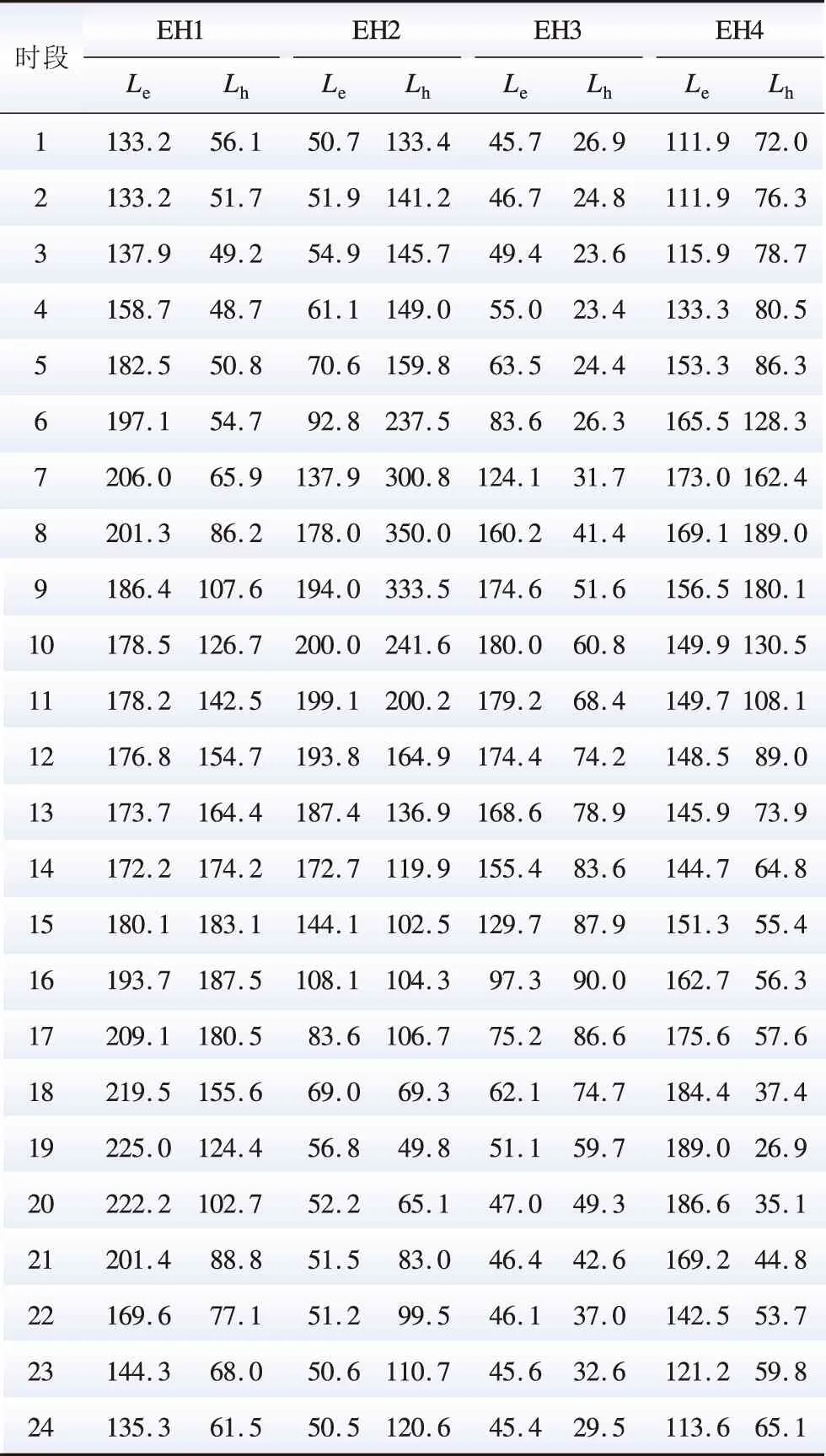
表1 耦合系统电/热负荷Table 1 Electricity and heat load of coupling systems kW

3.2 分布式优化调度结果分析

各个耦合系统优化调度方案如图7所示，可以看出基于本文所提分布式优化调度方法得到的调度方案满足耦合系统的相关运行约束。采用集中式优化调度方法进行对比验证，所得结果与本文所得方案完全一致。此外，从不同耦合系统的优化调度方案看，能源价格、负荷特性、设备运行特性、系统运行约束等因素对耦合系统的运行存在一定影响，具体分析如下：

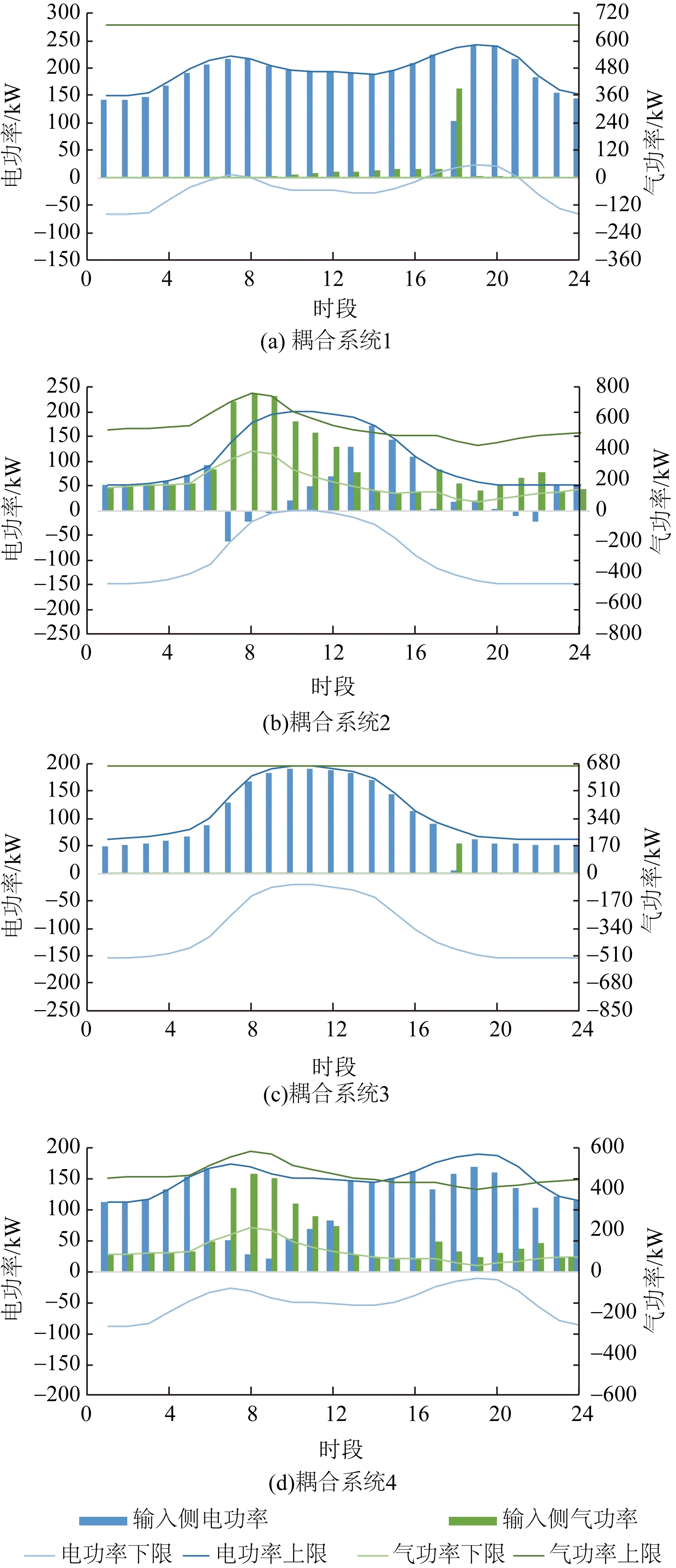
图7 耦合系统优化调度方案Fig.7 Optimal scheduling scheme of coupling systems

1) 第一类耦合系统。

第一类耦合系统的优化调度方案较为相似。在大部分时段，第一类耦合系统主要通过购电满足终端负荷，主要原因是第一类耦合系统中CAC产热效率远高于CHP机组[17]，因此电负荷主要通过电力变压器满足，热负荷主要通过CAC满足。考虑到时段10—17内EH1的负荷高于EH3，且EH1购电已达上限，因此有少量购气满足变压器无法完全供给的负荷。在时段18，由于电价为全天最高，从降低运行成本角度考虑，第一类耦合系统主要通过购气满足终端负荷。同时，由于该时段内EH1电负荷高于热负荷，对应负荷热电比小于1，负荷无法完全由CHP机组满足，因此，EH1在时段18仍需要购电。此外，从ICES系统整体角度考虑，在高电价时段若主要通过购电满足终端负荷，亦可能造成优化调度方案不满足系统运行的相关约束。

以时段18为例，基于本文所提方法与仅通过购电满足终端负荷的优化调度方案所得的配电系统电压分布与配气系统配气气压分布对比如图8—9所示。可见：若时段18仅通过购电满足终端负荷将造成配电节点电压越限，系统运行约束亦是影响耦合系统优化调度方案的重要因素之一。基于分布式优化调度框架所得的优化调度方案可满足ICES的相关运行约束，实现安全可靠前提下的经济最优运行。

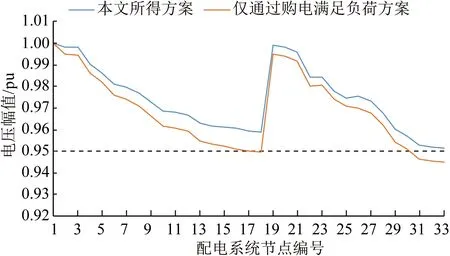
图8 不同优化调度方案下配电系统电压分布Fig.8 Voltage magnitude of electric distribution system under different optimal scheduling schemes

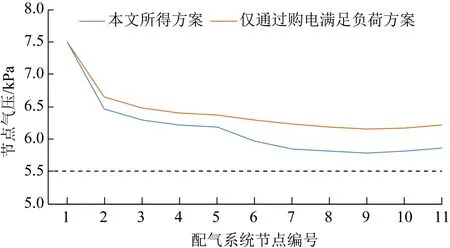
图9 不同优化调度方案下配气系统气压分布Fig.9 Node pressure of natural gas distribution system under different optimal scheduling schemes

2) 第二类耦合系统。

第二类耦合系统的优化调度方案在低电价时段较为相似。在时段1—6、13—16及23—24内，第二类耦合系统主要通过购电满足终端负荷，主要原因是这些时段内电价较低。在时段7—12内，随着电价的逐步提高，第二类耦合系统购电量有所减少，购气量有所增加。其中：EH2在时段7—12内热负荷高于电负荷，对应负荷热电比大于1，与CHP机组较为匹配[23]，因此购气接近上限，少部分不平衡负荷由电功率满足，如时段7—9内EH2将富余电量倒送入配电系统，时段10—12内EH2仍需从配电系统少量购电；EH4在时段7—12内热负荷低于电负荷，对应负荷热电比小于1，负荷无法全部由CHP机组满足，因此EH4在上述时段内购气功率小于EH2。在时段17—22内，EH2负荷热电比与CHP机组较为匹配，且由于该时段内电价较高，从降低运行成本角度考虑，EH2主要通过购气满足负荷。在时段17—22内，EH4电负荷有所增加，热负荷有所减少，负荷热电比进一步减少，CHP机组运行经济性不佳，购气功率接近下限，终端负荷主要通过购电满足。

与传统EH模型相比，本文所提基于状态变量的能量耦合矩阵在优化求解过程中能够更加准确地获得最优解。以EH1为例，时段17内不同分配系数下对应的优化调度方案如表2所示。可见：由于分配系数的取值范围为[0,1]，区间较小，导致不同分配系数下对应的耦合系统优化调度方案存在一定差异，分配系数仅变化0.001即会对优化调度方案产生较为明显的影响。因此，采用传统EH模型直接对分配系数进行优化可能使优化求解过程增加额外的时间开销。通过在EH模型中引入状态变量，能量耦合矩阵改写为常数矩阵，减少了重复求逆的计算过程。同时，状态变量代表了设备输入侧的功率，其取值区间明显大于分配系数的取值区间，有利于优化过程中更加快速准确地获取最优解。

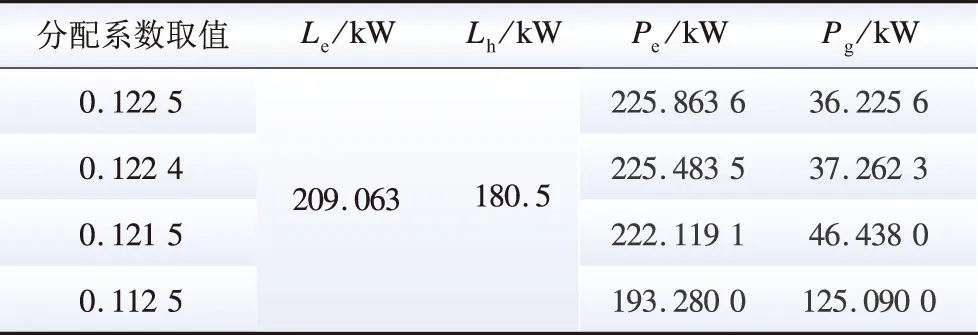
表2 时段17不同分配系数下EH1优化调度方案Table 2 Optimal scheduling scheme of EH1 under different partition coefficient for time period 17

在本文构建的分布式优化调度框架下，以EH1为例，其耦合变量在时段17内的收敛过程如图10所示。可见：通过引入共识变量，使得各子系统优化问题间具有一定的关联关系，避免了ICES优化解耦后耦合变量分立优化求解的情况。

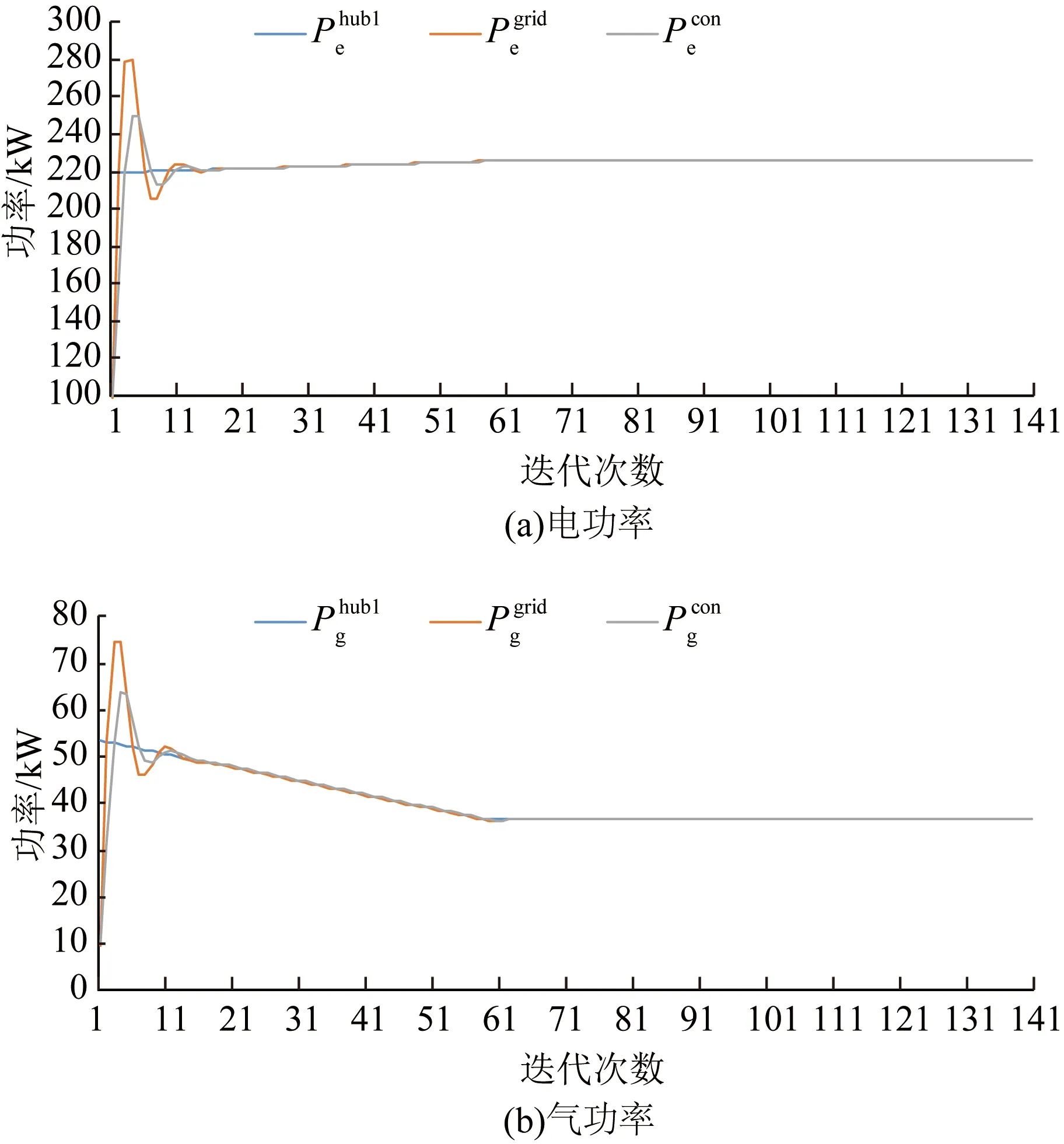
图10 时段17内EH1耦合变量收敛过程Fig.10 Convergence process of coupling variables of EH1 for time period 17

优化结果的残差收敛过程如图11所示，其中：残差收敛值以对数形式给出，便于详细分析收敛过程。可以看出：分布式优化调度框架下，原始残差及对偶残差在优化初期收敛速度较快；但随着迭代次数的逐渐增加，对偶残差的收敛速度逐渐放缓，在第35次迭代时，原始残差即已达到收敛误差，而对偶残差仍远远未收敛；迭代中后期阶段，对偶残差略微下降即会导致原始残差出现波动。上述现象是由原始残差与对偶残差所代表的物理含义不同所导致的：原始残差用于表征本轮迭代过程中耦合变量与共识变量间的匹配程度，如式(27)所示；对偶残差用于表征临近两轮迭代过程中耦合变量自身的变化趋势，如式(28)所示。耦合变量间通过共识变量相互关联，两者差值亦包含在增广拉格朗日函数中，每轮迭代过程中的耦合变量优化结果与共识变量差异较小，如图10所示。而耦合变量每轮的优化结果受到上轮迭代信息的影响，其变化趋势具有一定的不确定性，因此在分布式优化调度框架下，原始残差收敛速度快于对偶残差，对偶残差在迭代中后期收敛较慢。

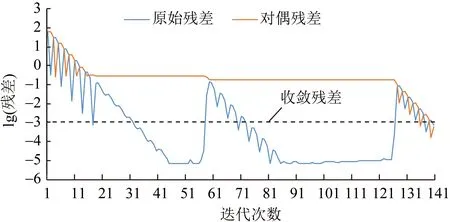
图11 时段17内ICES优化结果残差收敛过程Fig.11 Convergence process of residual of ICES for time period 17

4 结 论

本文提出了一种面向ICES的分布式优化调度方法，构建了配电系统、配气系统与耦合系统的数学模型，基于C-ADMM算法搭建了分布式优化调度框架，以系统运行成本最小化为目标，并考虑不同子系统的运行约束，实现了ICES优化调度的分布式求解。结果表明：本文构建的分布式优化框架可提供与传统集中式优化方法相同的调度方案，并有效减少了不同能源系统间运行参数的信息交换。此外，与传统EH模型相比，基于状态变量的耦合系统模型具备更高的求解精度，有利于提高分布式优化框架下的C-ADMM算法的求解效率。主要结论如下：

1) 基于本文所提的ICES分布式优化调度方法考虑了不同能源系统的运行约束，实现了分布式框架下ICES的经济最优运行，减少了系统运行参数在不同运营主体间的大规模交换，保证了用户的信息安全性。

2) 本文所提C-ADMM算法可根据不同用户主体特点灵活对ICES优化调度问题进行拆分，通过对各子系统优化调度问题并行求解，可兼顾不同运行主体的利益。

3) 耦合系统的优化调度方案受到能源价格、负荷特性、设备运行特性、系统运行约束等多方面因素的影响，通过在系统模型中引入状态变量能够在一定程度上提高优化求解的计算精度和效率。

能源价格以及多能负荷的不确定性会对ICES的优化调度产生影响。未来工作将研究ICES的分布式随机优化调度方法，通过在优化调度模型中考虑预测数据的不确定性，使得优化调度方案在不确定性环境下具有更好的经济性。