一道圆锥曲线模考题的再思考和拓展

安徽省合肥市第一中学 (230601) 谷留明

文[1]中笔者对合肥2019届高三第一次教学质量检测数学(理)第20题进行了研究，得到一些教学启示.此后，笔者经进一步思考,对文[1]中的部分研究有了新的方法，得到本文中的一些拓展结论.

1 问题再现

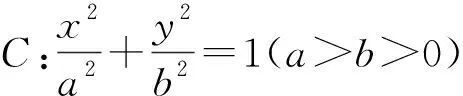
文[1]中，笔者分析了命题人所给参考答案的突兀性，并给出了另外两种较为自然的方法,既然至少有这两种较为自然的解法,那么参考答案里怎么会想到先证OM⊥ON?为何把这种方法作为参考思路?有无其它解法?背后有何“蹊跷”?所以，笔者文[1]中对该考题，用参数方程的方法进行了变式研究.这里用更为常用的解析法再次进行研究.

先给出原考题的常规解析法.

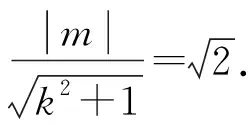
这个解法直译直叙,简单自然,可以说是基本方法.虽然运算量稍大一些,但这正是圆锥曲线解答题的特点,数学运算也是数学六大核心素养之一.

2 变式研究的新方法

变式1 圆O改为x2+y2=1,其它条件不变.试判断|PM|·|PN|是否为定值.

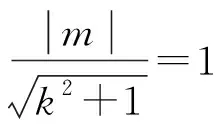
3 结论拓展

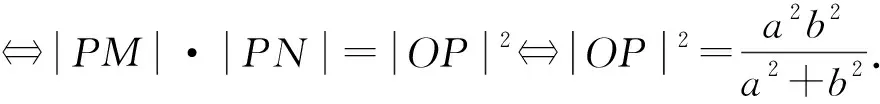
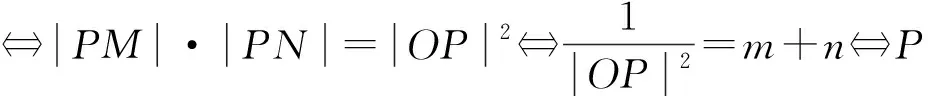
证明:设M(x1，y1),N(x2，y2).

由这些结论,命制类似的题目也就不足为奇了,参考答案的思路也就有了根据.但是这些结论并非课程所要求的必须掌握的基本定理,选方法三作为参考答案很是不妥.笔者在讲评这道题时,结合自己的心得,逐步引导学生去思考,激发学生的钻研精神,突出了对逻辑推理、数学运算、数学抽象这三大数学核心素养的培养.

4 问题引申

结论3 抛物线y2=2px(p>0)上有两点M，N,O为顶点,OM⊥ON,OP⊥MN于P,则lMN过定点Q(2p,0),且点P的轨迹是以线段OQ为直径的圆x2+y2=p2(除原点O外).

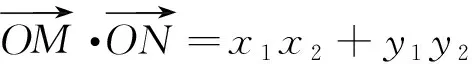
评注：此结论中轨迹虽然也是圆,但证明方法与圆的位置等显然与结论2有所区别.一方面结论2中,张直角弦所对的点O是有心圆锥曲线的对称中心,而抛物线不是有心圆锥曲线,结论3中点O是抛物线的顶点.另外,结论3中得到lMN过定点.那么,在有心圆锥曲线中,顶点张直角弦所在直线是否过定点,以及顶点在此直线上的射影的轨迹是什么？以左顶点为例,得到以下结论.

圆中的相关结论比较简单,这里不做赘述.另外,还可以探讨圆锥曲线的焦点张直角弦所在直线有何结论.