基于树形结构模拟的乡村高密度建筑群规划

钟运峰

(陕西理工大学土木工程与建筑学院，陕西 汉中 723000)

1 引言

自上个世纪末期，我国乡村建筑不断向高度发展，当前中国乡村已经完全卷入到全球化发展和开放体系中[1]。乡村建筑不断“借用”城市建筑的开发功能模式，造就了大量的规范化建筑。规范化乡村建筑因为自身突出性特征和超大的尺寸容量，很容易帮助人们建造出清晰的空间认知和确实的空间方位感。但是因为乡村经济原因，乡村边界规模一般小于城市，而自上个世纪90年代，乡村建筑如雨后春笋般在乡村拔地而起，建筑数量激增，其建筑领域涉及到经济、土地、规划等多种原因。但是因为政策和组织原因，许多乡村建筑的建设没有考虑布局的合理性，便直接落地， 大量的乡村建筑经过盲目的建设和发展以后，严重影响了乡村原有的地域机理。目前大量的城市乡村缺乏有序规划，导致乡村建筑逐渐向高密度无序化发展，乡村空间结构也开始混乱[2]。为了增强乡村建设的有序性，需要对乡村高密度建筑进行密度合理性的有效规划。目前现有的规划方式均需要借助模拟建筑图像，通过图像差分确定规划区域。图像差分就是根据当前图像的自身特征条件例如图像纹理、图像灰度、图像颜色、图像区域、图像轮廓等数据信息，将其划分为不同的数据资料点或者资料区域，再将研究适用的部分从图像数据中提取出来分析的过程。目前现有的乡村高密度建筑规划方法根据图像划分，一般可以分为帧间差法和背景减除法和光流法[3-5]。以上几种方法在背景图像的支持下通过评估函数，实现乡村建筑群规划。但是因为规划函数准确性差异，其最终的规划效果并不理想。由此设计采用一种基于树形结构模拟的建筑群规划策略，依靠差分图像和树形结构模拟相合性结果，输出评估函数，实现乡村高密度函数的建筑规划。

2 基于树形结构模拟的乡村高密度建筑规划

与传统建筑规划相似，设计规划方法同样需要借助当前乡村建筑群的差分图像。通过应用树状结构模拟，拆分评估密度函数，实现建筑规划。密度估计是概率论中的精度科目，主要指对未知密度参数的评估活动，属于非参数检验方法之一[6]。在乡村建筑群中，因为存在不同的建筑种类科目，所以在实际应用过程中， 不同建筑种类对应了差分图像， 低维和高维不同的线性关系，这种线性关系具有不可分解模式。数据差分的过程可以看做是低纬度数据映射到更高维度的系列空间里[7]。

而建筑群规划的最终目的就是利用树形结构，针对差分图像不同维度的参数进行评估，确定密度函数，其过程包括输入变量的输入、最优宽窗选择等，其输出值为密度规划最终函数，即为规划结果。其整体流程如图1所示。

图1 建筑规划流程图

2.1 树形结构模拟算法

设计依靠树形结构模拟算法，对当前差分图像初始密度估计算法的相合性进行检验。密度估计算法相合性检验一般又称为KS检验。主要基于乡村建筑群下多分辨率差分图像Kolmogoiov定理分布数据，通过拟合度寻优，确定参数检验算法。该方法通过对比不同建筑图像背景下的累积频数分布，检验建筑样本分布函数和假设分布函数，是否处于当前统一的背景下。简单的说KS检验是为了判别不同乡村建筑样本图像分布函数的匹配度，为以后建筑密度评估和建筑群规划确定图像背景。KS检验属于非参假设检验，在检验过程中，不需要数据样本的分布管理情况和样本基础，具有极高的适应性和稳定性[8]。

设计针对乡村建筑多分辨率差分图像像素点一维单一样本数据进行检验。也就是说通过对比样本经验的分布函数即当前原假设函数和密度累积分布函数进行比较，从而确定当前村建筑规划方法背景拟合度的适应情况。其具体检测步骤如下：

Step1：设原假设函数为Fn(x)，密度积累分布函数为G(x)，则有

(1)

Step2：根据式(1)构造建筑图像样本检验统计量

KS=max(|Fn(x)-G(x)|)

(2)

如果H0为真实数据，则有KS具有较小趋势延伸数据，此时表明当前假设原函数和建筑密度积累分布函数的拟合度较好；反之如果H0为假，则有KS具有较大趋势延伸性数值，此时表明当前假设原函数和密度积累分布函数拟合度较差。在G(x)如果处于连续分布且H0为真，则可以获取极限分布函数如下

(3)

Step3：设定明显的函数水平阈值a，也就是说样本数据临界值和图像像素点拒绝域边界为a。

Step4：计算检验样本P值，与阈值a进行数据比较，在通过h值刻画；

Step5：分析判定样本数据，确定接收和拒绝假设的结果，当P值大于a值的时候，原假设接收，反之当P值小于或等于a值的时候，原假设拒绝。其详细流程如图2所示。

图2 相合性分析流程

2.2 最优宽窗数据值的选定

最优宽窗h的数据取值会直接影响建筑密度评估结果，理论上h值会随着建筑差分图像样本数据n的增大而不断降低，当n趋于无穷，则h值趋于0。在建筑差分图像相合性确定的情况下，如果宽窗值的取值太低，则样本区间内的样本点会减少，这样会导致随机性影响增大[9]。此时获取的密度函数虽然可以反映多分辨率建筑图像差分出现的样本点信息，但是其曲线为不光滑的折线段；反之如果宽窗h值的取值过大，样本区间内的样本点会不断增多，可以导致建筑差分图像的像素点对核函数值的差距不断缩小，不用样本点的密度函数数值平均化影响增大，此时的密度函数曲线虽然光滑，但是结果分辨率较低，无法直观的反应出数据所包含的全部信息数据。

(4)

Ih(x)主要是在数学的角度，对于最优宽窗解进行求取，一般情况下Ih(x)最小值所对应h值的偏导数，其极值点即为当前图像数据的最指点，其推导过程如下

(5)

(6)

先对进行推导，其整体推导过程如下

(7)

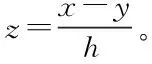
(8)

确定B(x)值后，继续对V(x)值展开计算，其推导过程如下

(9)

综上，将上述式(8)(9)分别带入到式(6)中，可以确定最终的推导表达式为

(10)

式(10)被称为渐进式积分方差误差算法，当MISE为最小值的时候，对应的h值为最终推导出的最优宽窗值。且存下以下等式关系

(11)

上述推导过程主腰是应用积分均方误差的形式获取当前建筑差分图像宽窗最优值的数据求取过程。设计通过MATLAB求解最优宽窗值，主腰是基于积分均方误差算法，由此获取的宽窗值为最优宽窗值，此时的建筑密度评估结果最好。

2.3 输出规划结果

上述理论过程完成了相合性分析和最优宽窗数据的选取。经过大量的实验数据证实，如果加工后的建筑图像样本足够大，则建筑密度最优评估下的函数具体形式对建筑图像当前概率密度评估的结果影响会缩小因为此次研究的对象为建筑差分图像，所以设计采用GK作为评估核函数和初始函数实现最终结果输出

(12)

引入建筑坐标值M得到函数

(13)

根据上述初始函数，通过无条件分位数回归的形式，进行建筑密度函数评估。设计以RIF为无条件分位数回归的基础模型

(14)

式(14)中，RIF(q0，y，Fy)是被解释变量分布函数F在对应的分为点上的执行分位数，根据中心影响函数，按照叙述定义可以得到最终的数据值为

(15)

式(15)q0表示无条件分位数。利用差分图像的条件期望值，进行数据迭代，可以获取以下公式

(16)

利用RIF无条件分位数回归一般会具有以下判定，依靠以下步骤，完成仿真评估。首先评估计算当前建筑差分图像能够通过统计量获取的回归分数，并根据回归分数的偏导数获取乡村建筑间距函数

(17)

上述公式为最终的密度函数，依靠该密度函数引入当前乡村建筑密度的实际值，即可实现密度重新规划。

3 仿真及结果分析

因为此次研究的主题是多分辨率差分图像的非参数核密度评估方法，考虑实验环境因素等情况，此次实验运用神经网络系统搭建仿真测评信息回馈平台，获取了预测图像的200个分位数，作为核密度估计的输入变量，通过求取并对比预测差分图像的概率密度曲线图，确定最终的测评结果。

3.1 实验图像处理

为了实现建筑规划合理性仿真，在当前仿真系统中分别应用数字高程预处理模块、预配模块、像素整体偏移量确定模块、谱分析模块，以及增强配准模块。每个模块在实验室中的应用如下：数字高程预处理模块主要应用仿真软件外部DEM操作，负责建筑图片InSAR的处理。首先需要对主图像进行配准，生成SAR数值图像，模拟数值图像的雷达坐标信息，根据轨道信息基础获取模拟相位量。

预配模块首先需要将图像中所有的Burst影像进行合并，根据配准方法对应图像数值，经过ICC炼化结果坐标雷达后，确定高程信息。

应用像素整体偏移量模块查找对应序列表，对当前辅助图像进行采样调查，此外基于实验主图像和辅助图像之间的相位差，完成图像配准，因为这一过程时间周期较长，需要保证实验平台不会引入异常干涉信号，为了降低实验消耗量可以仅在相位上完成数据偏移。最后对图像进行增强配准，根据图像补偿信息引入配准误差，对当前模块处理后得到的主图像进行过程采样，获取BURST倾斜处理，划分上下频图像，针对下频图像进行辅助处理后，生成BURST像素差分干涉图， 并逐一进行像素点配准操作。通过ESD算法，补偿当前精度轨道引起的和参数配准误差，生成辅图像进行干涉操作。

3.2 实验建筑物参数及布局结果

为验证建筑布局规划的有效性及合理性，本文将通过实地测量，获取某村落的建筑布局分布情况，如图3(a)，利用本文方法进行布局优化。乡村建筑参数如表1所示。

图3 乡村高密度建筑群分布(俯视图)

表1 建筑参数设定

根据上述参数，并结合本文的建筑间间距函数，规划合理建筑群分布，分布结果如3图所示。

根据部分示意图，应用至实际乡村环境布局中，得到结果如图4所示。

图4 乡村建筑群分布实际应用

通过图4的实际应用情况可知，本文方法能够根据乡村群落的地形而给出合理的布局方案。如图4中的A，是根据地地势较为平缓的平原设计的矩形排列，而图4中的B所处地势较高，故经本文间距函数计算规划后，得到最佳分布方案为即八卦阵型。由此可知，本文方法具有较高的适应性。

3.3 布局结果的抗风性

为了验证上述设计规划方法的其它性能，将分析本文方法在自然条件下，风载荷对建筑布局的影响，以图3(a)为例，作为本次实验研究对象，得到分析结果，如图5所示。

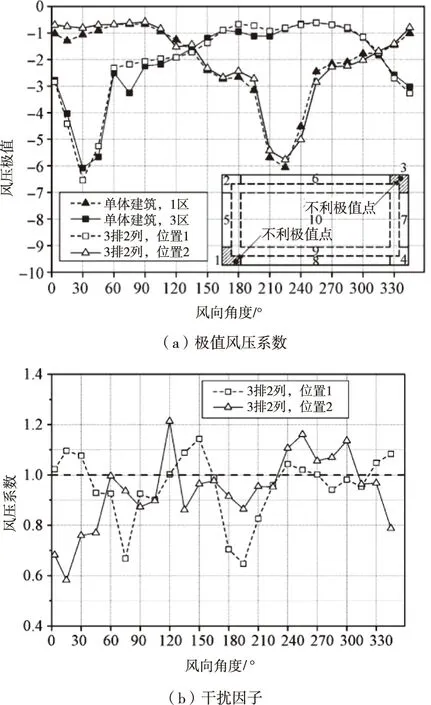
图5 建筑群屋面极值风压系数及干扰因子

分析图5可知，不同风向角度影响下本文规划的建筑群落布局无变化，且在极值风压状态的作用下该风向整体建筑对应风向相近，即总体建筑布局呈现遮挡缩减效应，能有效避免风荷载的影响，规划结果更具合理性。

4 结束语

从乡村发展规律上看，建筑群的兴起具有其必然性，然而建筑发展的过程中，合理密度下的规划布局是乡村建筑发展的核心点。设计为了有效解决乡村高密度建筑规划问题，基于树形结构模拟策略，提出新的密度规划方法，经过实验证实具有鲜明的优势性。