污水处理过程溶解氧浓度的有限时间抗扰控制

魏 伟，张莹莹，刘载文，左 敏

(北京工商大学人工智能学院，北京 100048)

1 引言

溶解氧(dissolved oxygen， DO)浓度是污水处理过程的关键变量之一，有效控制DO浓度至关重要[1]。然而，污水处理受进水流量、组分、浓度、温度等诸多因素的影响；同时，复杂的生化反应亦增加了其非线性和不确定性，这些都给DO浓度控制带来了极大的挑战[2]。

为有效控制DO浓度，人们进行了大量研究。PID控制[3]结构简单、易于实现，但因其无法有效处理非线性[4-5]而性能不佳。为获得更好的污水处理效果，模型预测控制[6-7]、专家控制[4]、模糊控制[8]、人工神经网络[9]、模糊神经网络[10，11]等相继用于溶解氧控制。模型预测控制精度受限于模型精度，为获得精确模型，需要辨识整个系统的模型[5]。有限的专家经验[1]限制了专家控制的效果。模糊控制提高了控制精度，但缺乏学习能力限制了其控制精度的进一步提高[12]。神经网络具有自主学习能力[13]，但也存在过拟合的问题[14]。

为此，结构简单、对数学模型依赖小、便于工程实现的控制算法，对污水处理过程控制非常必要。韩京清先生提出的自抗扰控制(active disturbance rejection control， ADRC)[15]利用扩张状态观测器(extended state observer， ESO)估计系统内部不确定性和外部扰动，并通过控制律将其补偿，获得了良好的控制性能，广泛应用于各领域。同时，考虑到收敛速度是控制系统的关键指标之一[16]。为此，文献[17]设计有限时间扩张状态观测器并应用于动中通天线伺服系统。文献[18]结合有限时间稳定理论与动态补偿线性化方法，提高系统的响应速度和抗干扰能力。本文针对污水处理过程的不确定性和扰动问题，改进有限时间观测器，以提高溶解氧浓度控制效果。

2 系统描述

污水处理1号基准仿真模型(Benchmark Simulation Model no.1， BSM1)由欧盟科学技术与合作组织和国际水协会共同建立，为污水处理过程控制策略提供评价标准。BSM1由2个厌氧池，3个好氧池和1个二沉池组成，其结构如图1所示[19]。

图1 BSM1结构

第5个反应池的DO动力学为[19]

(1)

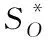
(2)

(3)

(4)

其中，SS为易降解底物，XB，H，XB，A分别为活性异养、自氧生物量，SNH为铵盐浓度，相关参数见表1[19]。

表1 污水处理部分工艺参数

3 有限时间抗扰控制设计

设计改进型有限时间状态观测器(modified finite-time extended state observer， MFTESO)，结合有限时间控制(finite-time control， FTC)，形成改进型有限时间自抗扰控制(modified finite-time active disturbance rejection control， MFTADRC)，其结构如图2所示。

图2 改进型有限时间自抗扰控制

3.1 有限时间扩张状态观测器

含模型信息的有限时间扩展状态观测器(finite-time extended state observer， FTESO)为[17，20]

(5)

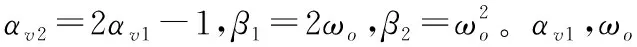
3.2 改进型有限时间扩张状态观测器

观测器的分数幂决定了其收敛速度，修正观测器输出估计误差的分数幂，可设计MFTESO为

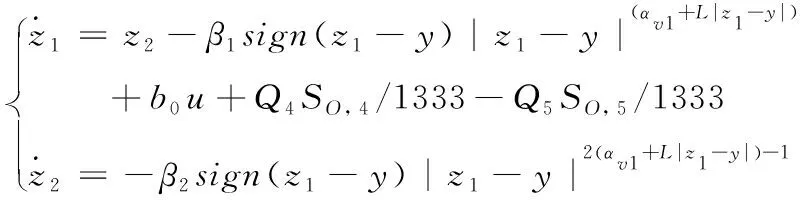
(6)

式中L为可调参数。

当1/2<αvi+L|z1-y|<1且βi>0，i=1，2时，观测器有限时间收敛，且收敛时间取决于αv1，L，ωo以及初始估计偏差e(0)=z1(0)-y(0)。

为证明观测器(6)是有限时间收敛的，先给出三个引理。

引理3.1[21]：若

(7)

θi=iθ1-(i-1)，1≤i≤n

(8)

那么系统关于(i-1)θ1-(i-2)，1≤i≤n，有(θ1-1)齐次度。

引理3.2[22]：对于系统

(9)

若存在矩阵

(10)

满足dii>0，i=1，2且DA(e)为正定对称矩阵，那么系统(9)在原点是渐近稳定的。

引理3.3[17]：若系统具有齐次度d<0且系统在原点是局部渐近稳定的，则该系统全局有限时间稳定。

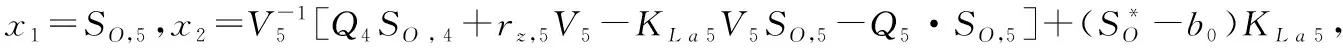
(11)

其中b0为控制增益，H(t)是总扰动的变化率，u是控制量。

设计二阶有限时间扩张状态观测器

(12)

其中

χi(·)=βisign(·)|·|αvi+L|·|，i=1，2

(13)

其中αvi，L，βi，b0待定。定义状态估计误差为ei=zi-xi，i=1，2。通常，总扰动及其导数信息未知，不妨令H(t)=0。由系统 (11)和观测器(12)，可得估计误差方程

(14)

调整αv1，L，βi(i=1，2)，使误差动力系统(14)全局有限时间收敛。有如下定理

定理3.1：若误差动力系统(14)同时满足齐次性、渐近稳定性以及

(15)

则误差动力系统(14)是有限时间收敛的，且时间T依赖βi，αvi，L和估计偏差e(0)=z1(0)-y(0)。

证明: 令

1/2<αv1+L|z1-y|<1

(16)

同时

(αvi+L|z1-y|)=i(αv1+L|z1-y|)-(i-1)，1≤i≤2

则系统关于(i-1)(αv1+L|z1-y|)-(i-2)，1≤i≤2具有度(αv1+L|z1-y|)-1的齐次性。

令e=[e1，e2]T，误差动力系统(14)可写为

(17)

式中，

(18)

其中F=|z1-y|(αv1+L|z1-y|)-1>0。令

(19)

取d11=ε1，d22=ε2，εi>0，i=1，2，那么

其中，

D11=ε1β1F+d12β2F2，D21=-d12β1F+ε2β2F2

使DA(e)为对称正定矩阵，则

(20)

于是

(21)

即

(22)

那么

ε1=η→0

(23)

将(23)代入(21)可得

(24)

使DA(e)正定，需d12>0，即

β1>0，β2>0

(25)

于是

(26)

那么，矩阵D取为

可见，D为F(估计误差e)的函数。

定义误差系统(14)的李雅普诺夫函数为

(27)

其导数为

(28)

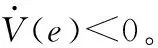
因此，由引理3.2知，误差系统(14)在原点渐近稳定。

选取参数使1/2<αv1+L|z1-y|<1成立，误差系统的齐次度为[(αv1+L|z1-y|)-1]<0。于是，由引理3.3可知，误差动力系统(14)(即扩张状态观测器(12))是有限时间收敛的。

3.3 有限时间控制

参考文献[16]及图2，设计有限时间控制律

u0=kpb0sign(r-z1)|r-z1|α1

(29)

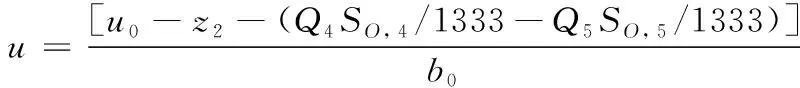
(30)

其中kp,ki,α1和b0是可调参数，r是设定值，u为控制量，z1是y的估计值，z2是总扰动的估计值。

4 数值仿真

表2 控制参数值

采用绝对误差积分(integral absolute error， IAE)，误差平方积分(integral square error， ISE)，最大绝对误差Devmax(maximum error)以及总耗能(overall cost index， OCI)定量比较控制性能及相应能耗[19]。

(31)

(32)

Devmax=max{|r-y|}

(33)

OCI=AE+PE+5SP+3EC+ME

(34)

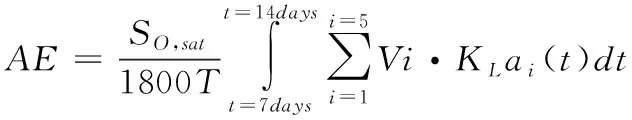
(35)

+0.008·Qr(t))dt

(36)

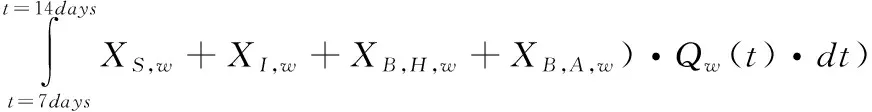
(37)

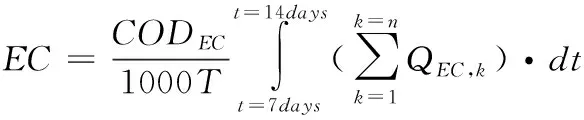
(38)

(39)

其中，r为设定值，y为第5个反应池的溶解氧浓度(变量信息详见文献[19])。

以下给出三种天气时，PI、FTADRC及MFTADRC的溶解氧调控效果及控制信号，并定量比较算法间的性能差异和能耗。

4.1 晴天

晴天时的系统响应和控制量如图3所示

图3 晴天时的系统响应及控制量

图3(a)所示响应表明，晴天时，MFTADRC的跟随误差最小。图3(b)显示三种方法的控制量相似。因此，用相似的控制量，MFTADRC能更好地跟随设定值。

由表3知，晴天时，与PI和FTADRC相比，MFTADRC的总能耗增加了3.67×10-3%和6.11×10-4%，而ISE降低了99.3%和79.2%；IAE降低了93.9%和42.6%；Devmax降低了88.5%和58.3%。可见，MFTADRC以相似的能耗，获得了更好的溶解氧浓度跟随效果。这表明，MFTADRC能够更快、更准地估计总扰动，进而保证更好的调控效果。

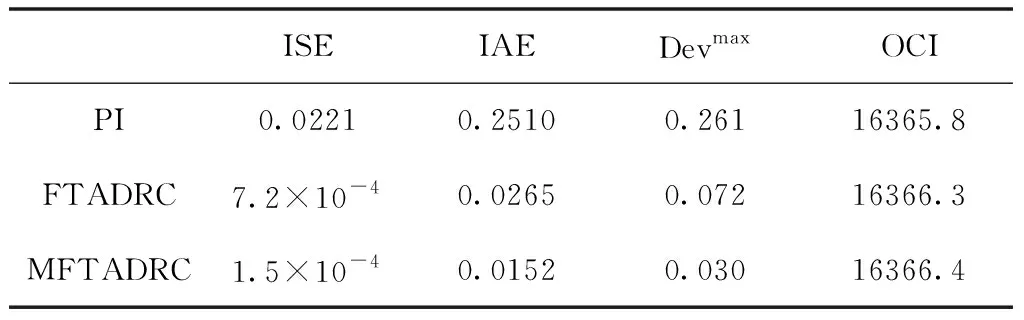
表3 晴天时三种方法的性能指标

图4表明，MFTADRC以相似的控制量获得了更好的溶解氧控制效果。表4给出了跟随误差及能耗的定量比较结果。

图4 雨天时系统响应和控制量

表4 雨天时三种方法的性能指标

表4数据表明，雨天时，MFTADRC比PI的总能耗上升了3.13×10-3%，比FTADRC的总能耗上升了6.26×10-4%。然而，与PI和FTADRC相比，MFTADRC的ISE降低了99.4%和75.6%，IAE降低了94.4%和38.9%，Devmax降低了89.0%和60.3%。可见，在能量消耗几乎相同的情况下，MFTADRC对溶解氧浓度的调控能力优于PI和FTADRC。同样表明MFTADRC估计总扰动的能力更强，调控溶解氧的效果更好。

与图3，图4相似，图5同样显示在相似的控制量作用下，MFTADRC的响应更接近设定值，溶解氧调控效果更好。表5也给出了控制性能和能量消耗数值。

图5 暴雨天时系统响应和控制量

表5 暴雨时三种方法的性能指标

同样，表5显示出MFTADRC的能耗与PI和FTADRC的能耗相近(增加了2.90×10-3%和5.80×10-4%)，但是其误差指标，ISE降低了99.3%和77.0%，IAE降低了94.0%和40.6%，Devmax降低了88.5%和58.3%。数据同样表明，在能量消耗几乎相同的情况下，MFTADRC因具有最好的总扰动估计能力而具有最佳的溶解氧调控性能。

为更直观地显示MFTESO的估计效果，图6给出了三种天气下实际总扰动和总扰动估计情况。

图6 实际总扰动与总扰动估计情况

图6表明MFTESO可准确估计系统总扰动，进而保证MFTADRC的调控效果。

5 结论

针对污水处理过程的不确定、强扰动问题，本文设计了一种改进型有限时间扩张状态观测器。综合有限时间控制和改进型有限时间扩张状态观测器，设计改进型有限时间自抗扰控制，有效克服各种扰动因素对溶解氧浓度的影响而获得更好的溶解氧控制效果。