基于2态Pauli量子游走的图像加密算法

杨宇光，王茜茜

(北京工业大学 信息学部，北京 100124)

目前，人们每天收到的信息中有约75%的信息为图像信息.图像信息暴露于公共视野，很容易受到攻击，其安全性受到社会关注.混沌加密算法存在安全隐患，有很大的改进空间.量子计算具有超强的并行计算能力，能够大幅提升图像处理速度，因此图像加密逐步从经典方案扩展到量子方案.

量子游走具有初值敏感性、不可预测性和伪随机性，可用于伪随机数生成器，因此基于量子游走的图像加密具有广阔的应用前景.文献[2]设计了基于1维双粒子量子游走的灰度图像加密算法.文献[3]提出了基于受控1维双粒子量子游走的灰度图像加密方案.文献[4]基于受控交替量子行走提出的伪随机数生成机制，已成为量子彩色图像加密协议的组成部分.

在最近的研究中，学者们将加密机制与明文信息关联.密钥随明文变化而变化，使加密结果对待攻击的密文没有任何参考意义.文献[5]的加密系统中的置乱操作与明文相关，用图像的部分像素信息置乱其他的位置像素.文献[6]提出一种基于超混沌的双图关联加密算法，对其中一幅图像进行明文关联，对另一幅进行自适应比特操作.笔者提出基于2态Pauli量子游走的图像加密算法.基于2态Pauli算子的游走构建伪随机数生成器，利用伪随机序列对灰度值进行置乱.采用双向扩散提高安全性能，扩大密钥空间.

1 基于2态Pauli量子游走的伪随机数生成器

1.1 基于2态Pauli量子游走的伪随机数生成器

(1)

从(1)式可看出，概率与量子系统的初态间存在非线性映射关系，概率对初态具有敏感性，这为构建伪随机数生成器打下了理论基础.

(2)

(3)

(4)

2维概率为

(5)

该文构建的伪随机数生成器生成伪随机序列的步骤如下：

(1)运行量子游走模型，得到的概率为

(6)

其中：0≤

p

≤1.为方便起见，将概率转化成序列

S

={

p

,

p

,…,

p

1；

p

,…,

p

2；…；

p

1,

p

2,…，

p

}.(2)重复步骤(1)并将所有的概率序列

S

(

i

=1,2,…,

m

)组合成伪随机序列

k

={

S

,

S

,…,

S

}.

1.2 伪随机数生成器的伪随机性

1.2.1 递归性

递归量化分析(RQA)是分析递归性的有效手段.RQA可从以下方面进行：①确定度(DET)；②平均对角线长度(ADL)；③熵值(ENTR)；④层状度(LAM)；⑤捕获时间(TT).

图1为基于2态Pauli量子游走的伪随机数生成器的DET，ADL，LAM，ENTR，TT.文献[7]给定的标准为：给定适当的阈值后，DET及LAM的典型值均约为0.3；ADL及TT的典型值均约为3.从图1可看出，DET最大值为0.22，LAM最大值为0.25，TT最大值为3.4，ENTR最大值为3，均满足文献[7]的标准，这表明基于2态Pauli量子游走的伪随机数生成器生成的伪随机序列具有良好的统计特性.

图1 基于2态Pauli量子游走的伪随机数生成器的DET(a)，ADL(b)，LAM(c)，ENTR(d)，TT(e)

1.2.2 非周期性

尺度指数

i

可用于研究非周期性.尺度指数

i

的大小范围为0≤

i

≤1，周期序列的

i

接近0，非周期序列的

i

接近1.图2为基于2态Pauli量子游走的伪随机数生成器不同

r

下尺度指数与硬币算子参数的关系曲线.由图2可知，尺度指数的最佳值为0.95，可见伪随机数生成器得到的伪随机序列是高度非周期性的.

图2 基于2态Pauli量子游走的伪随机数生成器不同r下尺度指数与硬币算子参数的关系曲线

1.2.3 伪随机性测试

该文通过NIST SP800-22测试伪随机序列的随机性.设

P

-value的阈值

α

=0.01，若某系列的

P

-value大于此阈值，则该序列可通过测试.表 1为NIST SP800-22的测试结果.由表1可知，所有

P

-value均大于

α

，表明所有的伪随机序列均通过了测试.

表1 NIST SP800-22 的测试结果

2 基于2态Pauli量子游走的图像加密算法

2.1 基于2态Pauli量子游走的密钥生成

设该文伪随机数生成器生成的伪随机序列为

K

={

k

,

k

,…,

k

}，其中

m

和

n

分别为图像的高和宽.由于伪随机序列值位于(0，1)，像素值位于(0，255)，因此加密前需将伪随机序列值扩展至(0，255)，其计算公式为

k

′=mod(

k

×10,256).

(7)

计算得到的

K

′={

k

′,

k

′,…,

k

′}将作为图像加密的密钥序列.

2.2 图像加密算法

该文所提出的图像加密算法结构如图3所示.

图3 该文图像加密算法结构图

2.3 加密过程

加密过程的具体步骤如下：

(1)使用SHA-256得到明文图像

A

的哈希函数值，伪随机数生成器中的参数

r

取该哈希值.使用2.1节所述方法得到密钥序列

K

={

k

,

k

,…,

k

}和

Q

={

q

,

q

,…,

q

2}.(2)利用密钥序列

K

={

k

,

k

,…,

k

}，进行Arnold置乱操作得到图像

B

.置乱操作将明文图像像素坐标(

x

,

y

)变换为(

x

,

y

).(3)将置乱后的图像

B

均分为4块，标记为

E

,

E

,

E

,

E

.进行

E

′=

E

⊕

E

,

E

′=

E

⊕

E

′,

E

′=

E

⊕

E

′,

E

′=

E

⊕

E

′

(8)

操作后，将

E

′,

E

′,

E

′,

E

′按原始分割顺序组合，得到图像

C

.(4)将序列

Q

={

q

,

q

,…,

q

2}分为

Q

={

q

,

q

,…,

q

}，

Q

={

q

+1,

q

+2，…,

q

2}.

Q

={

q

,

q

,…,

q

}，

Q

={

q

+1,

q

+2，…,

q

2}分别用于正向扩散和逆向扩散.图像

C

经正向扩散和逆向扩散后得到密文图像

D

.

2.4 解密过程

解密过程是加密的逆过程，具体步骤如下：

(1)通过加密步骤中的(1)，得到解密密钥序列

Q

′={

q

′,

q

′,…,

q

′2},

K

′={

k

′,

k

′,…,

k

′}.(2)对密文图像

D

进行正向扩散和逆向扩散的逆操作，得到图像

C

′.(3)将图像

C

′分为4块，标记为

E

′,

E

′,

E

′,

E

′.进行

E

=

E

′⊕

E

′,

E

=

E

′⊕

E

′,

E

=

E

′⊕

E

′,

E

=

E

′⊕

E

′

(9)

操作后，得到图像

B

′.(4)对图像

B

′进行Arnold置乱的逆操作，得到解密图像

A

′，

A

′即为最初的明文图像

A

.

该文选取Lena，Baboon，Cameraman图像进行加解密操作.图4为Lena，Baboon，Cameraman的明文图像、密文图像及解密图像.由图4可看出：密文图像完全看不出原图的样子，有良好的加密效果；解密后的图像与明文图像相差无几，有较好的解密效果.

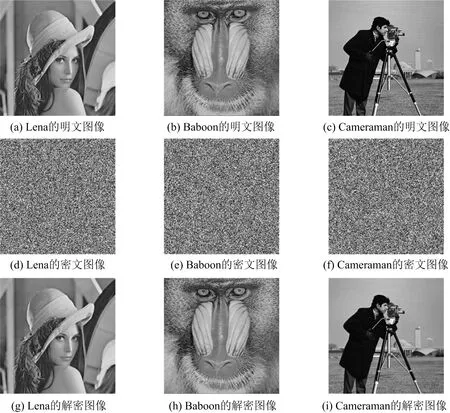
图4 Lena，Baboon，Cameraman的明文图像、密文图像及解密图像

3 基于2态Pauli量子游走的图像加密算法的性能

3.1 直方图

直方图的横坐标为灰度值，纵坐标为该灰度值的像素在图像中出现的次数.若密文图像直方图的像素出现次数绝大多数约为255，则认为加密算法有较好的加密效果.图5为Lena，Baboon，Cameraman图像加密前后的直方图.由图5可看出，密文图像各像素在图像中出现的次数绝大多数约为255，表明该文加密算法有较好的加密效果.

图5 Lena，Baboon，Cameraman图像加密前后的直方图

3.2 相关性

相邻像素的强相关性能为攻击者提供大量统计信息，好的加密算法应能降低像素间的相关性.该文随机选取了10 000组相邻像素，从水平、垂直和对角线方向进行相关性分析.相关系数计算公式为

(10)

其中：

x

，

x

′为相邻像素的灰度值.

相关系数平均值的计算公式为

(11)

其中：

H

，

V

，

D

分别为水平、垂直、对角线方向上的相关系数.

表2为不同明密文图像的相关系数.图6为Lena明密文图像分别在水平、垂直、对角线方向上的相关性分布.由图6和表2可知，明文图像的灰度值分布较集中、相关系数接近于1，密文图像的灰度值分布分散、相关系数接近于0，表明该文算法降低了相关性.

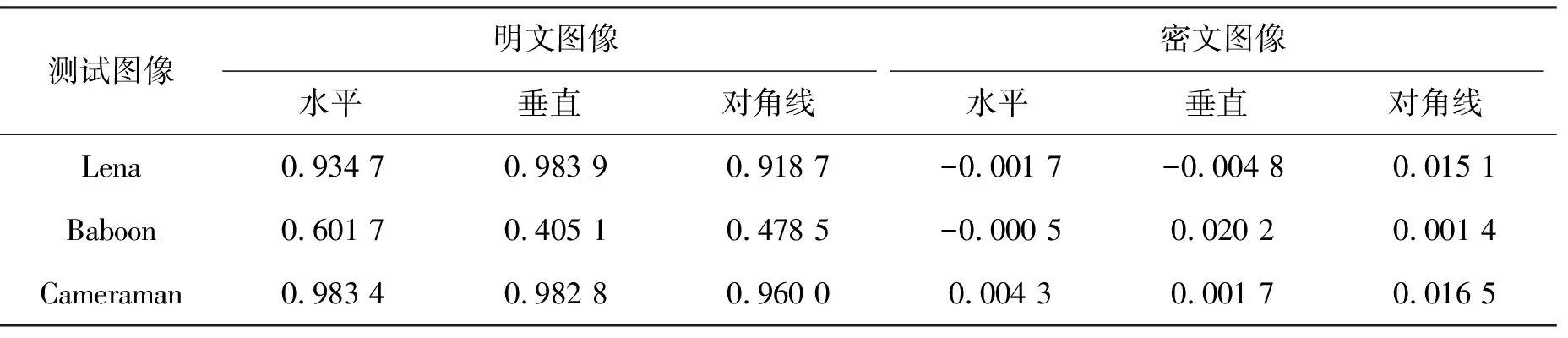
表2 不同明密文图像的相关系数

图6 Lena明密文图像的相关性分布

表3为Lena混沌图像加密算法及该文算法的相关系数，表4为Lake量子游走图像加密算法的相关系数.由表3，4可知，相对于文献[11-14]算法，该文算法相关系数的平均值最小，表明该文算法极大地降低了相关性，有较强的抵抗统计攻击的能力.

表3 Lena混沌图像加密算法及该文算法的相关系数

表4 Lake量子游走图像加密算法的相关系数

3.3 敏感性

敏感性有两种：密钥敏感性和明文敏感性.像素改变率(number of pixels change rate，简称NPCR)和一致平均改变强度(unified average changing intensity，简称UACI)是衡量图像差异的两种常见指标.与NPCR和UACI有关的表达式为

(12)

(13)

(14)

其中：图像

C

(

i

,

j

)，

C

(

i

,

j

)′的大小均为

M

×

N

.在密钥敏感性测试中，设置密钥参数为：

N

=1,(

α

,

β

)=(1,0),

θ

=π

/

2.加密Lena明文图像得到图7(a)；将

θ

调整为π

/

1.999 999 9，再次加密Lena明文图像得到图7(b).图7(c)为图7(a)，(b)的差分图像.差分图像图7(c)不全黑表明两图像间存在着一定的差异.对比图7(d)，(e)可知，密钥经过微小调整后无法正确解密，表明该文加密算法对密钥相当敏感.

图7 密钥敏感性测试

以Peppers加密为例，研究该文算法的明文敏感性.加密明文图像(图8(a))生成密文图像(图8(b)).在明文图像(图8(a))中随机选择1个像素，让其灰度值加1，用相同密钥加密调整后的明文图像，得密文图像(图8(c)).图8(d)为图8(b)，(c)的差分图像.经计算，得到两个密文图像的NPCR为99.65%，UACI为33.47%.表5列出了不同图像明文敏感性测试的结果.由表5可知，NPCR，UACI的数值均分别大于99.58%和33.42%，表明该算法有较好的明文敏感性.

图8 Peppers明文敏感性测试

表5 不同图像明文敏感性测试的结果

NPCR和UACI越大，加密算法越具有安全性.由表6，7可知，除文献[14]Lake图像的 NPCR外，该文算法的NPCR和UACI均高于文献[11-16]算法对应值.因此，相对于文献[11-16]算法，该算法具有较高的安全性.

表6 混沌图像加密算法及该文算法的明文敏感性测试结果

表7 量子游走图像加密算法的明文敏感性测试结果

3.4 信息熵

信息熵是描述信号随机特性的重要指标.理想状态下，256位完全随机信号的信息熵为8.信息熵的计算公式为

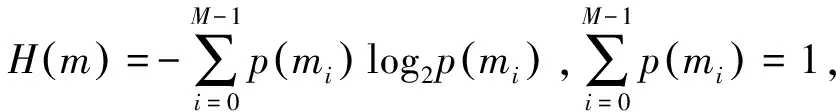
(15)

其中：

p

(

m

)为灰度值

m

出现的概率，

M

=256.由表8可知，该文算法密文信息熵均达7.997 2以上，最优值为7.997 7，非常接近理想值8.

表8 该文算法明密文图像的信息熵

由表9，10可知，该文算法密文信息熵平均值大于引用文献[12-16]的平均值，且十分接近理想值8.因此，相对于文献[12-16]算法，该文算法的密文图像具有较高的随机性.

表9 混沌图像加密算法及该文算法的密文图像信息熵

表10 量子游走图像加密算法的密文图像信息熵

3.5 密钥空间

安全的加密算法必须提供足够大的密钥空间，以保证攻击者无法在有效时间内找到密钥.该文伪随机数生成器理论上能生成无限多的随机数，由于计算条件的限制，提供的密钥空间是有限的.假设计算精度为10，根据初始条件和控制参数，算得该文算法的密钥空间约为2，可见该文算法能有效抵御攻击.

3.6 加密速度

该文算法的运行环境为：Windows 10，MATLAB R2018a，Intel(R)Core(TM)i5-8250U CPU @1.60 GHz 1.80 GHz.加密图像的平均时间约为0.335 s，比文献[12]的0.613 s短，可见该文算法的加密速度足够快.

3.7 鲁棒性

鲁棒性是衡量加密算法抗干扰能力的重要标准.该文通过噪声攻击和裁剪攻击测试加密算法的鲁棒性.峰值信噪比(peak signal noise ratio，简称PSNR)可度量两图像的相似程度，PSNR的计算公式为

(16)

其中：图像

f

(

i

,

j

)和

f

(

i

,

j

)的大小均为

N

×

N

.PSNR值越小，加密算法的抗攻击能力越强.

3.7.1 裁剪攻击

以Lena密文图像为例，通过3种裁剪比例的密文图像测试该文算法的鲁棒性.从表11可看出，不同裁剪比例的PSNR均较小，表明该文算法能有效抵抗裁剪攻击.由图9可知，该文算法能恢复图像的基本面貌.

表11 不同裁剪比例的PSNR

图9 抗裁剪攻击的鲁棒性

3.7.2 噪声攻击

除裁剪攻击外，图像还会受到噪声攻击.以Lena密文图像为例，分别添加强度为0.02的高斯噪声、强度为0.02的椒盐噪声、强度为0.1的均值噪声和强度为1的伽马噪声.由图10可知，解密图像能看出大致轮廓，原始信息基本被保留.从表12可看出，不同噪声的PSNR均较小，表明该文加密算法具有较强的抵抗噪声攻击的能力.

图10 抗噪声攻击的鲁棒性

表12 不同噪声的PSNR

4 结束语

笔者构建了基于2态Pauli量子游走的伪随机数生成器，提出了基于2态Pauli量子游走的图像加密算法.利用Arnold的置乱特性，让明文信息参与密钥生成过程.在置乱的基础上进行双向扩散，保证了密文图像的扩散性.与该文引用文献的加密算法相比，该文算法有较好的加密效果，有较强的抵抗统计攻击、裁剪攻击及噪声攻击的能力，有较高的安全性.该文算法的加密速度仍有提升空间，有待后续的改善和优化.