控制方向未知的非线性系统切换自适应全局快速有限时间控制

雷红臣，李小华*，刘 辉，何志江

(1.辽宁科技大学 电子与信息工程学院，辽宁 鞍山114051；2.中国三冶集团有限公司 电气安装公司，辽宁 鞍山 114003)

有限时间控制方法能使系统具有更快的收敛速度及更高的鲁棒性能, 故产出了大量非线性系统有限时间控制的研究成果.有限时间控制可分为精确有限时间控制和实际有限时间控制.这两种控制的主要区别是: 精确有限时间控制能保证系统的所有状态在有限时间内均收敛至平衡点, 而实际有限时间控制只能保证系统所有状态在有限时间内收敛至平衡点的邻域内.一般地, 精确有限时间控制又被称为有限时间控制, 实际有限时间控制又称为有限时间有界.随着研究的深入, 文献[7]提出了快速有限时间控制, 这种控制方法能使系统具有更快的收敛速度.

在众多的非线性控制系统中, 有一类系统的控制方向是未知的.控制方向与数学方程中与控制变量相乘的未知参数的符号相对应, 控制方向未知即该参数的符号未知.在实际生活中存在许多控制方向未知的系统,如船舶的航向控制、飞行器的姿态控制及多智能体的编队控制系统等.解决此类控制问题的方法主要有：Nussbaum增益、切换控制方法.Nussbaum增益方法, 只能使系统收敛至平衡点邻域内, 因此该方法不能解决控制方向未知的非线性系统的精确有限时间控制问题.然而，切换控制方法通过切换能找到正确的控制方向, 能实现精确有限时间控制.笔者提出一种新的切换自适应全局快速有限时间控制方法, 使闭环系统在有限时间内收敛至平衡点

x

=0而不是平衡点的邻域内, 满足全局快速有限时间稳定条件.

1 系统描述和预备知识

1.1 系统描述

考虑如下控制方向未知的非线性系统

(1)

(2)

假设2

虚拟控制系数

D

(

t

)满足

D

,min≤|

D

(

t

)|≤

D

,max,

(3)

其中: 未知常数

D

,min>0,

D

,max是一个已知的函数.

该文的控制目标为: 采用backstepping技术、快速有限时间稳定理论以及切换自适应技术, 针对系统(1)设计一个切换自适应快速有限时间控制器, 使该闭环系统全局快速有限时间稳定, 其所有状态轨迹在有限时间内收敛至平衡点.

1.2 预备知识

为了得到该文主要结果, 给出如下引理：

引理1

若系统存在一个

C

非线性函数

V

(

x

(

t

)),

t

∈[

t

,+∞),满足

(4)

则称该系统是快速有限时间稳定的, 且有

(5)

注1

引理 1可作为系统快速有限时间稳定的Lyapunov判据.

(6)

引理3

对于

x

,

j

=1,2,…,

n

和实数0<

l

≤1, 下面的不等式成立(|

x

|+|

x

|+…+|

x

|)≤|

x

|+|

x

|+…+|

x

|.

(7)

|

x

-

y

|≤21-|

x

-

y

|.

(8)

引理4

对于任意正实数

c

,

q

,

τ

和任意的连续函数

x

,

y

,

κ

≥0, 有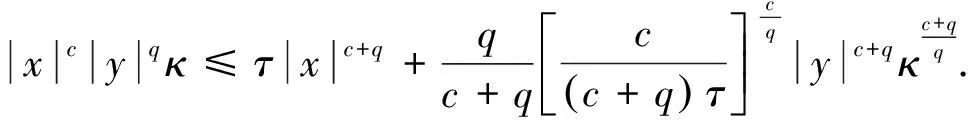

(9)

(10)

2 主要结果

2.1 控制器设计

选取坐标变换为

⋮

(11)

第1步 选取Lyapunuov函数为

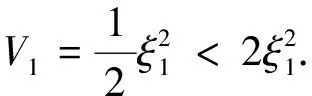
(12)

对

V

求导后, 再根据假设1可得

(13)

(14)

将式(14)代入(13), 有

(15)

选择虚拟控制律为

(16)

将该控制律代入式(15), 有

(17)

(18)

第2步 选取Lyapunov函数为

V

=

V

+

W

,

(19)

其中

(20)

根据引理3, 可得

(21)

求

W

的偏导数，得

(22)

(23)

由引理3, 可得

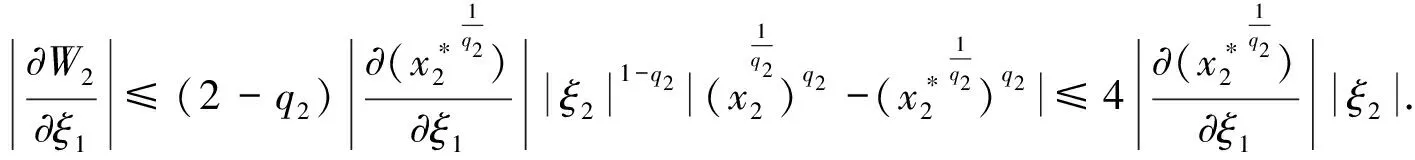
(24)

对

V

求导后, 再根据式(18)～(20)和(22)，可得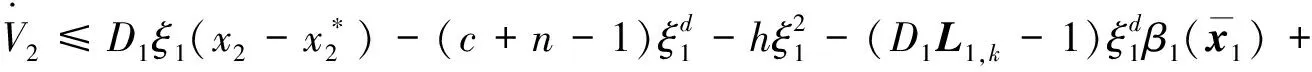

(25)

下面对式(25)中的几个多项式进行处理.

(26)

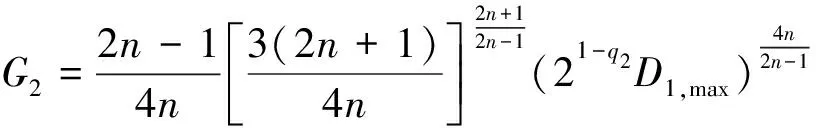
为了处理式(25)中的其他项, 先引入如下结论：

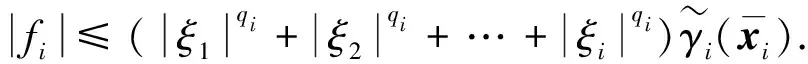
(27)

结论2

存在一个适当的

C

函数

C

,≥0, 使下式成立

(28)

结论1～2的证明见文献[3]中的推论3～4的证明.

(29)

其中

(30)

将式(26),(29)～(30)代入式(25), 得

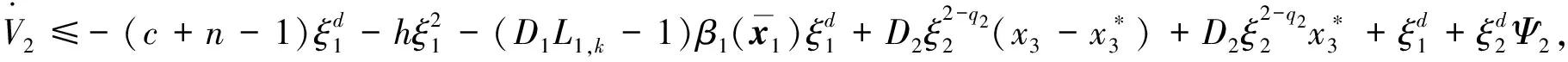
(31)

其中:

Ψ

=

G

+

F

+

φ

.

选取虚拟控制律为

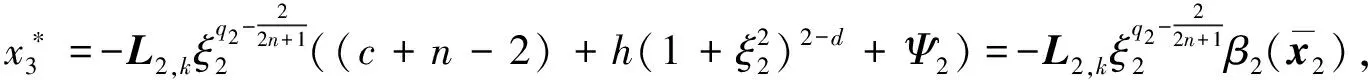
(32)

将式(32)代入式(31), 可得

(33)

为了下面第

i

(

i

=3,4,…,

n

-1)步推导的方便, 这里根据第1, 2步的推导, 给出如下推论：

(34)

则有

(35)

证明

在第2步, 由式(19)～(21),(33), 可知式(34)～(35)成立.假设推论1在第

i

-1步成立, 即有

(36)

(37)

下面利用式(36)～(37)，证明推论1在第

i

步也成立.对第

i

步, 由于

V

=

V

-1+

W

,

(38)

其中

(39)

则有

(40)

(41)

(42)

其中: 1≤

j

≤

i

-1. 结合式(36),(38),(40), 有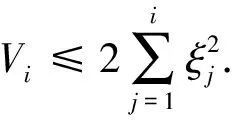

(43)

根据引理3, 式(42)进一步被放缩为

(44)

根据式(37)～(39),(41), 可得

(45)

下面, 对式(45)中的几项多项式进行处理.

(46)

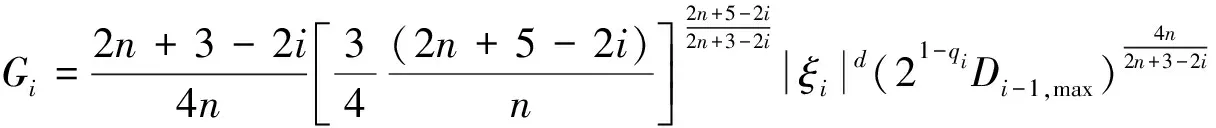
(47)

其中

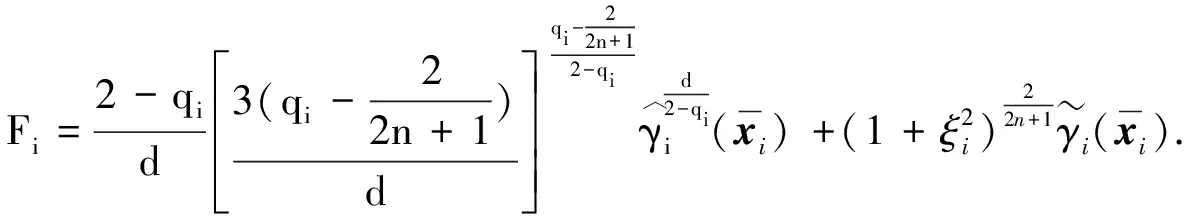
(48)

将式(46)～(48)代入式(45), 有

(49)

其中:

Ψ

=

G

+

F

+

φ

.

选取虚拟控制律为

(50)

将式(50)代入式(49), 得

(51)

由式(43),(51), 可知推论1成立.

利用推论1, 可得第

n

步的推导如下：第

n

步 选取Lyapunov函数为

V

=

V

-1+

W

,

(52)

其中：

V

-1和

W

在式(36)和(39)中已通过

i

=

n

被定义.显然有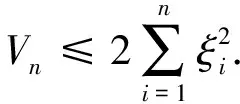

(53)

对(52)式，求导得

(54)

由推论1知

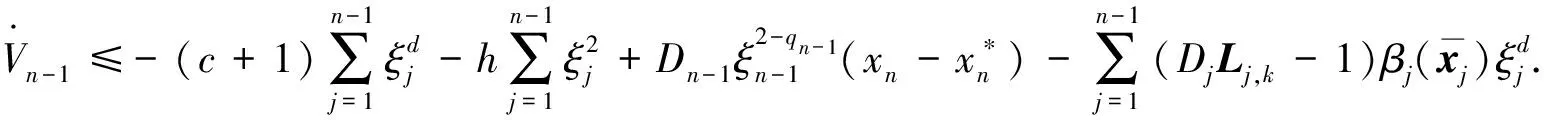
(55)

选取系统控制律为

(56)

由式(55)～(56), 可得

(57)

2.2 切换自适应律设计

为了达到全局快速有限时间稳定的目的, 按照引理1的条件, 对式(57)做进一步处理.选取,使式(57)中的最后一项大于零, 则有

(58)

(59)

由式(59)及引理1可知, 系统满足全局快速有限时间稳定的判据.若式(57)中的最后一项小于零, 说明控制方向不对, 需进行切换.

(60)

(61)

(62)

按引理1中条件, 设计切换自适应律为

(63)

其中:

μ

是设计参数，且

μ

>0;

w

(

t

,

t

,

x

(

t

),

μ

)的表达式为

(64)

定义切换的时间序列为

t

+1=inf{

t

|

t

>

t

,

V

(

x

(

t

))>

w

(

t

,

t

,

x

(

t

),

μ

)}.

(65)

2.3 全局快速有限时间稳定性分析

定理1

对于满足假设1～2的系统(1), 若选取系统的控制律为式(16)，(50)，(56), 切换自适应律为式(63), 则系统(1)是全局快速有限时间稳定的, 且停息时间满足

(66)

证明

首先证明在切换自适应律式(63)的作用下, 下面的不等式成立

(67)

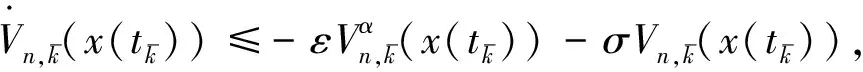
(68)

(69)

可见, 在所设计的切换自适应律作用下, 式(67)总能成立.在此条件下,式(59)成立, 即系统(1)是全局快速有限时间稳定的.

由切换自适应律的定义可知, 在每个切换区间均有

V

(

x

(

t

))≤

w

(

t

,

t

,

x

(

t

),

μ

),

(70)

则

V

(

x

(

t

))有界.

根据引理1, 可知系统的收敛时间是有界的,收敛时间为

(71)

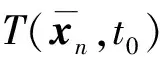
3 仿真实验

为了验证该文控制方法的有效性, 这里采用文献[14]中的仿真系统, 其数学模型为

(72)

选取控制参数为:

θ

=

θ

=1,

k

=

k

=1,

R

=

R

=0.55,

V

=

V

=0.3,

F

=0.3；选取设计参数及函数为:

c

=0.6,

h

=1,

μ

=1,

H

(

k

)=0.37×(

k

+3)；选取系统初始状态为：=[0.5,-0.5]；选取控制系数的上界为:

D

=2.5,

D

=2.

根据定理1, 得到该系统对应的控制器, 对系统进行仿真实验.该控制器的仿真结果如图1～4所示.图1～4分别给出该文及文献[14]的系统状态、控制输入、切换参数、切换条件函数值的仿真结果.

图1 系统状态 图2 系统控制输入

由图1可知：该文的切换自适应律能保证系统的所有状态在有限的时间内收敛到平衡点；该文状态收敛速度比文献[14]更快.由图2可知：与文献[14]相比, 该文不需要更大的控制作用即可满足快速有限时间的要求.由图3可知，切换参数为2时,该文和文献[14]控制器的控制方向和系统的实际控制方向均相同，但该文切换时间更早.由图4可知，该文切换条件函数的收敛速度比文献[14]更快.上述仿真实验结果表明: 该文控制方法具有优越性和有效性.

图3 切换参数 图4 切换条件函数

4 结束语

该文研究了控制方向未知的非线性系统切换自适应全局快速有限时间镇定问题.将快速有限时间控制与逻辑切换控制相结合, 提出了新的切换自适应全局快速有限时间控制方法.设计了控制方向未知的非线性系统切换自适应全局快速有限时间控制器, 该控制器能保证系统的所有状态在有限时间内收敛至平衡点, 且有更快的收敛速度.此控制效果是Nussbaum增益方法达不到的.