去椒盐噪声的新型图像复原模型

宋瑞丽,谷 芳,孟 鸽,李 涛

(1.郑州经贸学院 公共教学部，河南 郑州 451191; 2.郑州财经学院 统计与大数据学院，河南 郑州 450000;3.陆军炮兵防空兵学院，河南 郑州 450000)

在计算机视觉和图像处理过程中，图像去噪发挥着至关重要的作用，去噪算法的好坏直接决定了图像分割和配准等后续工作的效果，因此研究图像去噪问题具有重要的现实意义.在众多的噪声问题中, 论文主要关注椒盐噪声去除问题.

椒盐噪声是一类常见的脉冲噪声，往往产生于数据存储或信号传输过程中.对于被椒盐噪声破坏的图像，其噪声像素为动态范围内的最大值和最小值，人们针对这一特点提出了众多去除椒盐噪声的方法.中值滤波是最早被提出的一种有效的椒盐噪声滤除算法，但由于该滤波器是利用局部窗口像素的中值代替中心像素的值，因此在去噪的同时也对无噪声的像素进行了修改，从而导致丢失纹理细节和边缘模糊.为了克服上述缺点，学者们提出了几种改进中值滤波，如自适应中值滤波、基于均匀性信息的中值滤波、加权中值滤波.这些改进模型首先识别出可能的噪声像素，然后使用中值代替中心像素的值，同时保持非噪声像素不变，因此在一定程度上克服了中值滤波器的缺陷.然而，上述方法并没有考虑噪声的分布特征，因此在噪声水平较高的情况下不能很好地恢复图像边缘及细节信息.随后，文献[7]提出基于低秩表示模型来改进上述缺陷，其基本原理是将观测矩阵分解为稀疏矩阵和低秩矩阵，并通过数值实验算法显示其去噪效果优于中值滤波.但是，该方法会产生纹理细节丢失等问题.

不同于上述方法，近年来基于能量泛函的变分正则化方法已被证明在噪声消除和边缘保留之间能取得良好的平衡,其中最成功最基本的正则化模型是由Rudin等提出的ROF(rudin osher fatemt)模型，其针对脉冲噪声普遍采用TVL1模型，即全变分(total variation，简称TV)项加L1范数项.该模型中的TV项不惩罚图像中的不连续性, 而且其对应的欧拉方程扩散是沿着边缘切线进行的，因此可以有效保留图像边缘.然而，由于TV正则项是基于梯度的L1范数，过分惩罚稀疏性，经常将平滑信号转换为分段常数，因此产生所谓的“阶梯”现象.为解决上述问题，学者们提出了许多改进，如高阶全变分模型、广义全变分模型等.

最近，基于低秩表示和全变分正则化的思想，文献[14]提出了一种新的去噪模型——全变分和核范数正则化模型.该模型通过有效地耦合图像矩阵的低秩性和TV正则项的保边性来得到较好的去噪效果.然而，通常意义下图像具有多结构特征，TV正则项中的梯度算子并不能有效耦合图像的局部特征，为此论文提出一种具有鲁棒性的去椒盐噪声的新型复原模型.在提出的模型中，通过将全变分项中的梯度算子加权以增强其沿图像边缘切线方向的扩散能力，并结合图像的低秩性，进而改进文献[14]中的去噪效果.在数值算法上，由于所提模型是具有可分性结构的凸优化问题，因此采用交替方向乘子法(alternating direction method of multipliers，简称ADMM)求解，并能从理论上保证算法的收敛性.数值实验表明，论文所提模型在去噪效果上具有更好的鲁棒性.

1 相关工作

1.1 预备知识

(1)

其中:

s

,

s

分别表示灰度值的最小值和最大值.

=,=diag({

σ

}1≤≤),

(2)

其中:,分别表示

n

×

r

和

n

×

r

的正交矩阵，

σ

表示奇异值.对于任意的

τ

≥0，其奇异值收缩算子为

D

():=(),()=diag({

σ

-

τ

})，其中符号

t

表示取

t

中大于零的部分，即

t

=max(0,

t

).

1.2 全变分去噪模型(TVL1)

Chan等在文献[19-20]的启发下提出了经典的TVL1去噪模型

(3)

其中:

f

为观测图像，

λ

为正则化参数.

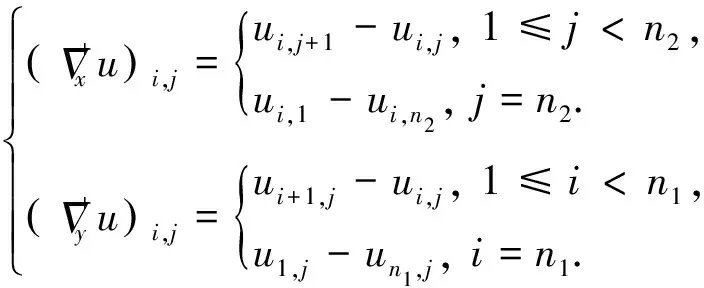
(4)

(5)

尽管TVL1模型可以有效地保留图像边缘信息，但由于TV正则化不能区分跳跃区域和平滑过渡区域，因此在去噪过程中会产生“伪边界”，即阶梯现象.

1.3 全变分和核范数正则化模型(total variation nuclear norm,简称TVL1NN)

为了在利用图像稀疏性的同时能有效刻画结构特征，文献[14]提出了全变分和核范数正则化模型(TVL1NN)

(6)

其中:‖·‖定义为所有奇异值的和.此模型TV项和核范数项能有效刻画图像的结构稀疏性，可以有效去除噪声.然而由于全变分项中的梯度算子仅能刻画图像水平和竖直方向的信息，从而导致在保持图像局部结构特征时缺乏自适应性.

2 改进模型与求解算法

2.1 改进模型

基于上述模型中存在的问题，论文基于TVL1NN模型提出一种新的去噪模型，即各向异性全变分和核范数正则化模型(anisotropy total variation nucler norm，简称ATVL1NN)

(7)

其中：=diag(

t

,

t

)，

t

，

t

为尺度函数，其依赖于图像的局部信息，因此可以用来刻画图像的局部特征，即

(8)

2.2 求解算法

在数值上，ATVL1NN是凸优化问题，因此存在全局最优解.然而模型的非光滑性，导致直接数值求解比较困难.一种有效的方法是利用其可分结构通过分离变量的方法求解，即通过引入辅助变量将其转化为下述约束优化问题

(9)

为了求解上述问题，在增广拉格朗日意义下，可将其转化为下面的鞍点问题

(10)

其中:

α

,

α

,

α

,

α

为拉格朗日乘子；

β

,

β

,

β

,

β

为罚参数；〈·，·〉定义为内积.由于该鞍点问题是多变量优化问题，因此可以利用交替方法乘子法求解，即通过固定剩余的变量来更新其中的一个变量

(11)

下面考虑各个子问题的具体求解过程：

(1)求解子问题

p

.由于该问题为经典的

l

-

l

问题，因此可以利用压缩阈值法求解，其显式解为

(12)

(2)求解子问题

q

.为了求解

q

子问题，需要引入下面的定理.

(13)

基于上述定理，子问题

q

的闭形式解为

(14)

(3)求解子问题

w

.该问题类似于求解子问题

p

，即用压缩阈值法求解，其显式解为

(15)

(4)求解子问题

v

=(

v

,

v

).该问题为光滑凸优化问题，令

α

=(

α

2,

α

2)，

α

=(

α

3,

α

)，则其最优化条件为

(16)

上式方程组化简得

(17)

(5)求解子问题

u

.该问题为光滑凸优化问题，其最优性条件为

(18)

在周期边界条件下，可以使用快速傅里叶变换快速求解

(19)

下面可将上述内容归纳为用交替方向乘子法求解模型ATVL1NN，具体求解过程如下：

初始化阶段：输入初始图像

u

=

f

，设置参数的初始值：最大迭代步数maxiter=500，相对误差

ε

=10，正则化参数

λ

，

λ

>0，令

k

:=0.迭代阶段(重复

k

次)：(1)

k

:=

k

+1；(2)通过(15)式更新子问题

w

；(3)通过(17)式更新子问题

v

；(4)通过(12)式更新子问题

p

；(5)通过(14)式更新子问题

q

；(6)通过(19)式更新子问题

u

；

终止条件估计:若相对误差小于10或迭代到达500步则算法终止；否则，返回迭代阶段.

3 仿真实验与分析

3.1 测试图像和平台

为了验证模型的有效性，将论文模型和两种不同的去噪模型(TGVL1和TVL1NN)进行比较.该节选取经典的256×256 House和Boat灰度图像以及512×512的Barbara和Mandrill灰度图像进行测试仿真，如图1所示.

图1 测试图像

由于这些测试图像均含有较多混合细节、纹理区域及分块光滑区域，因此可以验证文中所提模型的有效性.文中实验在Window7系统MATLAB 2016a上进行.此外，当连续两次迭代的相对误差满足‖

u

+1-

u

‖≤

κ

‖

u

+1‖，

κ

=1.0×10或迭代次数达到500次时，程序算法迭代终止.为了验证论文方法在图像去噪中的效果，采用MATLAB内置函数信噪比(signal to noise ratio，简称SNR)和结构相似性(structural similarity，简称SSIM)来评判复原结果.在通常意义下，SNR和SSIM值越大，表示去噪效果越好.此外，为了标准化图像，在实验中首先将初始图像归一化，然后使用MATLAB的内置函数“imnoise”分别添加30%，50%，70%的椒盐噪声.

3.2 不同模型之间去噪结果比较

对于图1中的前两幅图像(a)，(b)，分别加入30%,70%的椒盐噪声，得到信噪比分别为5.425 6,3.279 9 dB的含噪图像.表1给出了客观指标对比，列出了不同噪声水平下去噪图像的SNR和SSIM值.图2给出了主观效果对比，列出了使用3种方法得到的去噪图像以及局部区域放大图.

表1 不同噪声水平下复原图Barbara和Boat的SNR,SSIM值

由表1可知，不管是在高噪声还是低噪声的情况下，论文所提模型ATVL1NN的SNR和SSIM值都明显高于其他去噪模型，其中SNR值可高于其他方法0.34～1.43 dB.

为了更好地说明论文所提模型去噪效果的显著性，图2给出了视觉效果的主观评定，其中第一行展示了复原图像的去噪效果图，第二行展示了复原图像局部区域放大对比图.由复原图像可以明显看出：经TVL1去噪后的复原图像虽能很好地去除噪声，但却将局部细节信息过于平滑，从对应的局部放大区域能看到明显的“阶梯现象”，如Barbara的脸部以及Boat的桅杆过于模糊，纹理细节丢失严重；较TVL1相比，经TVL1NN去噪后的复原图像去噪效果有一定的改进，这是因为用以控制噪声稀疏性的L1正则项增强了核范数降维抗噪声的性能，但还不能很好地刻画细节信息，如局部放大图桌布的纹理信息和桅杆的截断现象.论文所提模型去噪效果是最好的，从局部区域放大图可以明显看出该模型充分保持了图像纹理细节信息，如明显看到桌布的斜条纹以及桅杆的方向信息.

图2 Barbara和Boat图像的主观效果对比图

对于图1所剩两幅图像(c)～(d)，仅考虑加入50%椒盐噪声的去除问题，分别得到信噪比为4.568 1,4.802 5 dB的含噪图像.表2给出了客观指标对比，列出了不同噪声水平下去噪图像的SNR和SSIM值.图3给出了主观效果对比，列出了使用3种方法得到的复原图像以及原始图像和复原图像之间局部区域残差图.

表2 不同噪声水平下House和Mandrill的SNR和SSIM值

由表2可知，论文所提方法在SNR和SSIM值上有明显优势，SNR值高于其他方法0.3～0.5 dB.图3为原始图像和复原图像之间的残差图.图3的第一行表示所有对比模型的复原图像，图3(a)和(a1)显示的图像出现了“油画”的视觉感受，这正是因为该模型中的梯度范数在图像光滑渐变区域惩罚较小跃迁信息时导致的,图3(b)～(c)，(b1)～(c1)整体视觉效果相差不大.下面将从残差图对其去噪效果进一步说明.

对于残差图像而言，较亮的区域代表较大的误差，较暗的区域代表较小的误差.图3的第二行表示所有对比模型复原图像与原始图像的残差图，与其他3种模型所示残差图相比，论文所提模型ATVL1NN显示最暗的残差图，表明论文所提模型具有最好的去噪性能.

图3 原始图像和复原图像之间的残差图

不管从客观的数值结果还是主观的视觉感受，论文所提模型都显示了最好的去噪效果：不仅将大部分噪声从图像中去除，同时也很好地保留了图像的纹理细节信息.

4 结束语

通过分析TV和低秩表示模型，针对它们的不足提出一种去椒盐噪声的新型图像复原模型.该模型具有TV去噪模型的优点，即可以更好地保持图像边缘信息，同时具有低秩表示模型的优点，而低秩性能更好地刻画图像细节信息.同时该模型在梯度算子中引入不同的权重参数惩罚

x

与

y

方向上的微分，因此在复原图像的过程中可以有效地保持图像结构特征.仿真实验结果表明，论文所提模型的去噪效果明显优于其他几个经典的去噪模型，在去噪的同时保留更多的图像细节与边缘信息.