分数阶不确定复杂网络系统滑模同步的两种方法
2021-11-17 03:03孟晓玲毛北行
安徽大学学报（自然科学版） 2021年6期
孟晓玲，毛北行
(郑州航空工业管理学院 数学学院，河南 郑州 450046)
复杂网络的同步，即网络之间的节点系统通过外部调控，状态逐步接近，最后达到全同的状态.网络同步是一种非常普遍而且十分重要的非线性现象，因此复杂网络系统的混沌同步已引起了人们的广泛关注.在投影同步的基础上，文献[7]研究了复杂网络系统的有限时间同步；通过设计合适的控制器，文献[8]实现了自适应非线性耦合网络的有限时间同步控制；文献[9]研究了复杂网络在脉冲信号下的网络同步问题.而随着分数阶微积分的发展，分数阶系统引起了广大学者的关注，并取得了不错的研究成果，但关于分数阶复杂网络系统滑模同步方面的研究结果还是比较少.在上述研究的基础上，论文研究了分数阶复杂网络系统的同步特性,在分数阶稳定性理论的基础上，设计了两种分数阶控制器和滑模面，实现了该系统的滑模同步.最后，利用MATLAB数值仿真，说明该方法的有效性.
1 预备知识
定义1
连续函数x
(t
)的Caputo分数阶导数定义为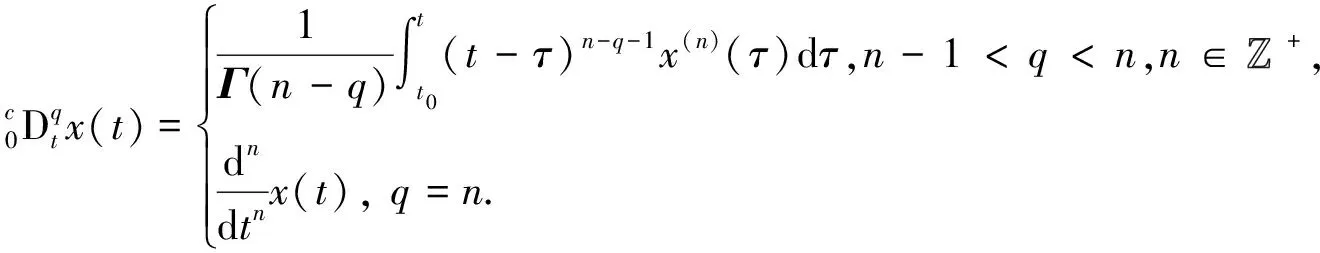
引理1
若x
(t
)为连续可微的向量函数，则
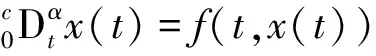
γ
(‖x
‖)≤V
(t
,x
(t
))≤γ
(‖x
‖);
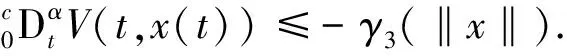
α
∈(0,1)，‖·‖表示向量范数,则该分数阶系统是渐进稳定的.
2 主要结果
考虑以下节点为N
个的复杂网络系统
(1)
以系统(1)为驱动系统，构造响应系统
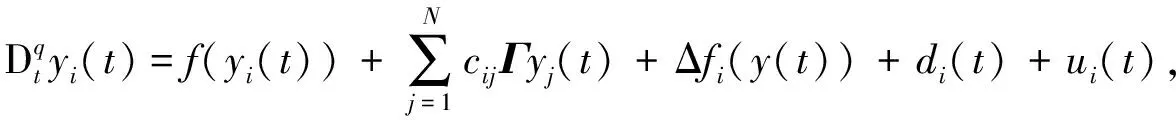
(2)
其中:Δf
(y
(t
))为不确定项，d
(t
)为外部扰动，u
(t
)为控制器.系统(1),(2)的同步误差为e
(t
)=y
(t
)-x
(t
),则
(3)
假设1
‖Δf
(y
(t
))‖≤m
,‖d
(t
)‖≤n
,m
>0,n
>0,i
=1,2,…,N.
假设2
‖Δf
(y
(t
))+d
(t
)‖≤λ
‖e
(t
)‖,λ
>0,i
=1,2,…,N.
定理1
在假设1,2下，构造滑模面为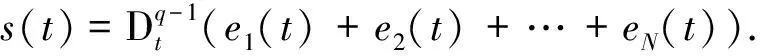
设计控制器为
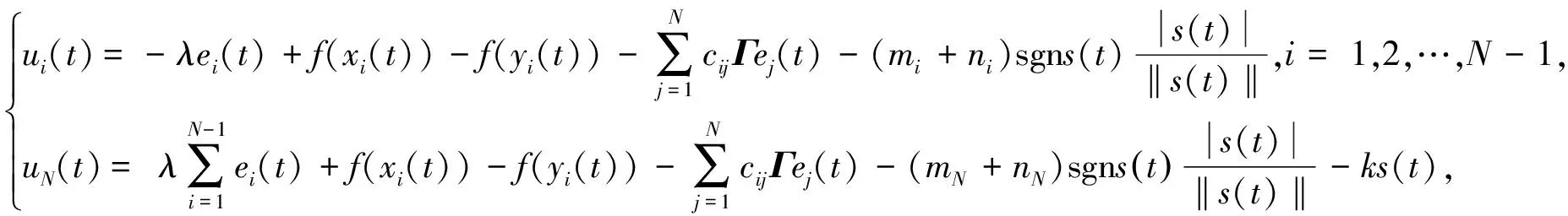
其中
sgn(s
(t
))=diag{sgn(s
(t
)),sgn(s
(t
)),…,sgn(s
(t
))},|s
(t
)|=(|s
(t
)|,…,|s
(t
)|)，则系统(1)与(2)是滑模同步的.
e
(t
)+e
(t
)+…+e
(t
)=0⟹e
(t
)+…+e
-1(t
)=-e
(t
).代入控制器，(3)的前N
-1个方程可写为
构造
由引理1和假设2知
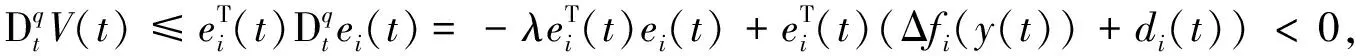
e
(t
)→0,i
=1,2,…,N
-1.代入控制器，方程(3)的最后一个方程变为
e
(t
)+e
(t
)+…+e
-1(t
)=-e
(t
)，从而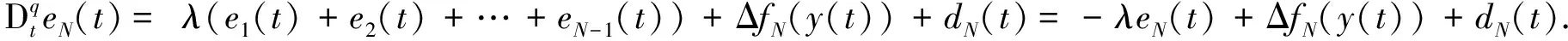
构造
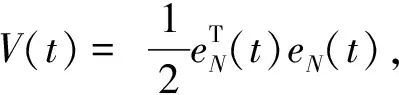
则由引理1和假设2,有
e
(t
)→0.
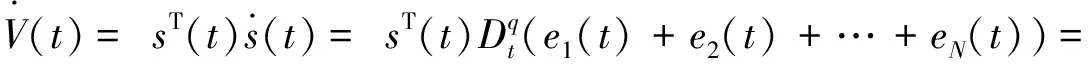
s
(t
)(-λe
(t
)-λe
(t
)-…-λe
-1(t
)+λ
(e
(t
)+e
(t
)+…+e
-1(t
))-
两边积分，得
s
(t
)→0，则e
(t
)→0.假设3
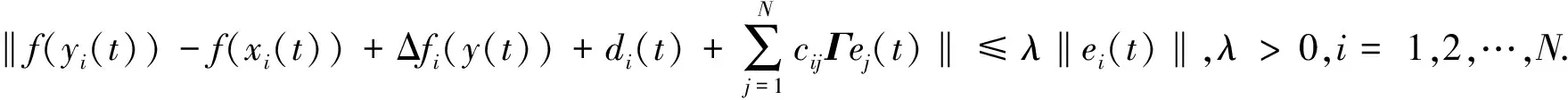
定理2
在假设3下，构造滑模面为
控制器为
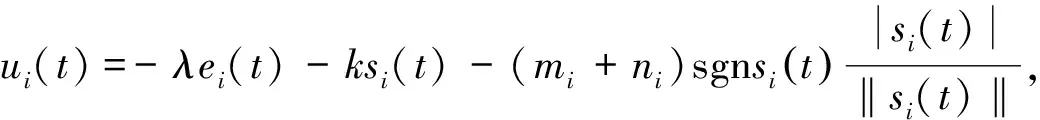
λ
>0为常数，则系统(1)与(2)是比例积分滑模同步的.
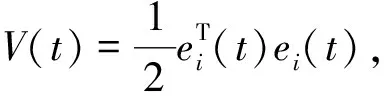
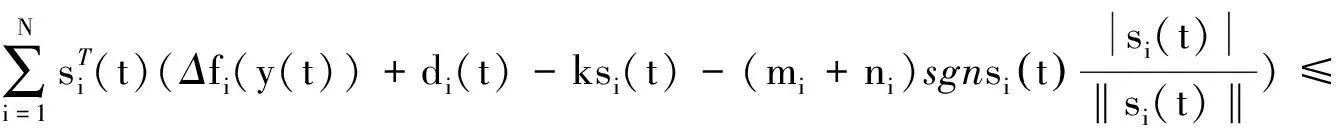
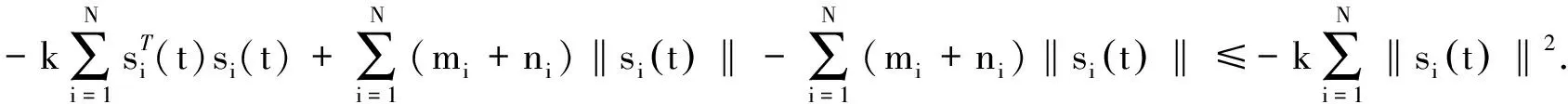
两边积分得
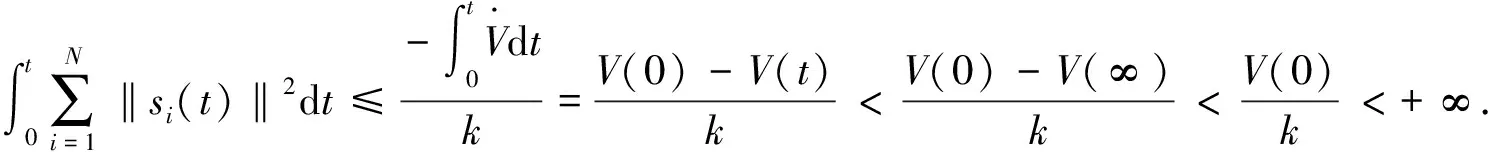
s
(t
)→0，则e
(t
)→0.3 MATLAB仿真
不妨取含3个节点的网络进行仿真
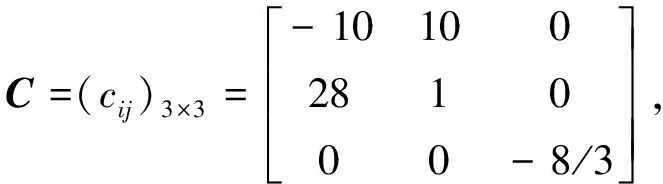
选取分数阶Lorenz系统为例，驱动系统为
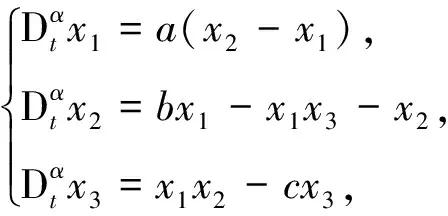
响应系统为
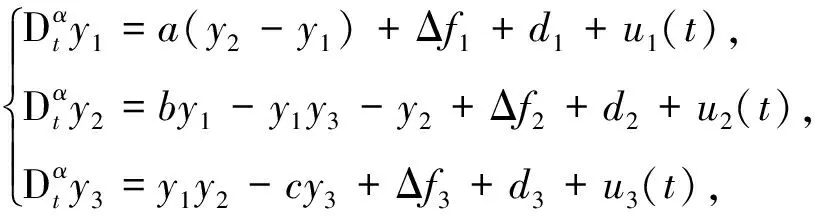
误差系统为
α
=0.93,a
=10,b
=28,c
=8/
3时，出现吸引子.
x
(0),x
(0),x
(0))=(1,2,-1)，步长选取为0.01 s，误差曲线如图1所示.
图1 定理1中的系统误差曲线
Δf
(y
)+d
(t
)=0.1sin(t
)y
+0.1cost
,Δf
(y
)+d
(t
)=-0.1cos(t
)y
+0.1cost
,Δf
(y
)+d
(t
)=-0.1sin(t
)y
+0.1cos(2t
).定理2中取滑模面和控制器为
u
(t
)=-λe
(t
)-ks
(t
)-(m
+n
)sgns
(t
)，(x
(0),x
(0),x
(0))=(1,1,-1).选取步长为0.01 s，误差曲线如图2所示.
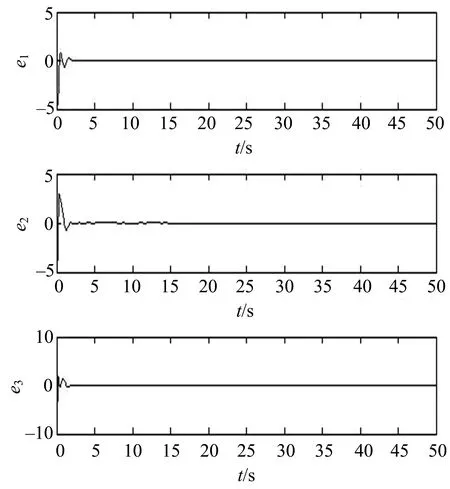
图2 定理2中的系统误差曲线
由图1，2可以看出，系统初始时刻误差相距较大，但随着时间推移，系统误差逐渐变小，且逐渐趋近于零，这说明系统取得了混沌同步.
4 结束语
与整数阶系统的稳定性理论相比，分数阶系统的稳定性理论还不是很成熟，又因为复杂网络本身的复杂性，让一些分数阶微分系统的稳定性理论很难得到直接的应用，因此进一步完善分数阶微分系统的稳定性定理，是值得研究的下一个课题.
