基于儿童视角启迪儿童的数学思考

王海燕

思考是儿童数学认知的关键，深入而持久的思考、深刻而理性的思维是人的核心素养之一。小学数学教学要立足儿童的学习需求，开发、整合学习资源，优化、丰富儿童的学习方式，促进他们的数学思考自然展开，有效拓展其认知的广度、宽度和深度，积极改善其数学思维。

一、儿童数学思考不足的样态扫描

在现实的课堂教学中，受教学环境、教学理念、教学机智、思维惯性等主客观因素影响，儿童开展数学思考在一定程度上还存在着一些比较突出的问题。

（一）条件干预，弱化儿童数学思考的参与

受传统教育观念影响，课堂上的“教”还没有完全让“学”，主要表现在：第一，教师不能正视儿童的学习能力，随意介入儿童的学习活动；第二，教师忽视儿童的认知基础，随心为儿童搭建学习的“脚手架”；第三，教师漠视儿童的学习规律，随便割裂其思考过程。“教”的过度介入对儿童的数学思考造成了干扰，导致儿童数学思考的参与度不高。

（二）碎片问答，窄化儿童数学思考的空间

《义务教育数学课程标准（2011年版）》将课程目标分为知识技能、数学思考、问题解决和情感态度四个方面，强调要以知识技能学习为载体，促进其他目标的达成。但是，在教学中，教师往往会忽视过程性目标的达成，更多地偏向于知识技能目标的顺向引导，以问答方式展开教学过程的现象屡见不鲜。教师课堂话语权的垄断，窄化了儿童数学思考的空间，影响了儿童数学思考的流畅性和深入度。

（三）指向单一，固化儿童数学思考的联结

儿童的思维和视角决定了其数学思考应该是多样的、多元的、立体的，且不同方法之间存在一定的逻辑性，打通不同方法之间的壁垒，可以让儿童获得对数学的深切感悟。但是，当前数学课堂的开放度还不够，儿童的数学思考常限于书本与已知，对学科理解不深。教学中对知识本质凸显不够，使得儿童视角站位不高，儿童的数学学习常常浅尝辄止，数学思考在低位往复。

儿童的数学学习一头连着个体内在已有的数学现实，一头连着儿童外在可以触摸的世界。在儿童不能凭借一己之力解决问题时，教师可以适时呈现一些有一定吸引力和适度挑战性的学习内容，引导学生理解与感悟。

二、基于儿童视角启迪儿童数学思考的策略

（一）明晰认知图式，找准数学思考的起点

孔子曰：“不愤不启，不悱不发。”要让数学学习真实发生，必须要让儿童理清原有相关认知，同时明确即将展开的学习任务和目标，在原有认知与新知学习之间建立起图式，图式越清晰，学生的学习基础就越牢固，数学思考就展开得越自然。

1.创设情境，生成关键问题。

现实情境是数学问题的载体和催化剂，不仅能让儿童亲近数学，感受数学与生活的联系，还能营造良好的数学思考氛围，帮助儿童较好地实现数学抽象，生成关键性问题。例如，教学苏教版五下《圆的认识》一课，面对学生没有备好圆规无法画圆的现实问题，教师相机提问：“没有圆规，用直尺能否画出圆？”大部分学生表示不能。于是，教师课件动态演示用直尺画圆的过程，即借助直尺描出到定点距离等于定长的点，当点无限多时，便组成了一个圆。从现实问题出发创设情境，激发儿童的认知冲突，进而通过比较与沟通画圆的方法，打开了儿童的视野，启迪儿童产生新的数学思考，使他们深刻理解了圆的概念本质。

（图2）

2.尝试解决，获得初步体验。

3.适当留白，促发认知需求。

留白是一种教学智慧，适当的留白是为了更好地补充。通过留白给儿童提供思考的时间与空间，有助于儿童自主发现问题和提出问题，并产生分析问题和解决问题的积极心理趋向，从而较好地实现认知由机械接受向有意义理解的转变。例如，教学苏教版六下《面积的变化》一课，在学生对将长方形按比例放大后面积的变化有了一定感知后，教师提出要求：“在方格纸上画出其他平面图形，将其按一定比例放大，比较放大后与放大前面积的变化，你有什么发现？”学生不仅列举了三角形、正方形、圆等学过的平面图形，还研究了不规则图形，丰富了对平面图形面积变化的认识。在此基础上，学生自主提出问题：“立体图形按比例放大后，体积比与长度比会有什么关系？”并通过推理得出了结论。教师随即课件呈现平面图形的二维性与面积变化之间的关系、立体图形的三维性与体积变化之间的关系。学生欣赏后脑洞大开，追问有没有四维图形。留白把“学”置于课堂中央，学生基于活动感知产生积极的学习需求，为后续学习奠定了良好的基础。

（二）拓宽儿童视域，激活数学思考的拐点

数学思考是由浅入深逐步打开的过程，这是由数学学科的逻辑性决定的。呈现具有一定吸引力和适度挑战性的学习内容，引导儿童展开理解与分析，可以拓宽儿童的视域。

1.追本溯源，领略“是什么”，延长数学思考。

概念教学虽然依附于具体情境，但不能浅尝辄止，满足于表象的建立和特征的把握，而要在学生充分感知的基础上，揭示其背后的内涵与本质，从学科的角度进行理解与把握，延伸数学思考的长度。例如，教学苏教版五上《认识负数》一课，通过创设温度计、海拔高度等具体情境让学生认识正数和负数后，教师通过课件动态演示，把温度计的刻度与海报的高度抽象成数轴，引导学生利用数轴这一数学化工具，将正数和负数放在原有自然数、分数、小数的概念中进行理解，从而形成对数的序列化认识。在具体情境中进行数学抽象是概念教学的重要环节，可以让学生的数学学习变得生动且深刻。

2.投石问路，欣赏“怎么办”，拓宽数学思考。

受经验和认识能力限制，在分析与解决问题时，儿童的思维容易固化，有时表现为面对问题束手无策，思维停滞不前；有时表现为对单一问题解决方法的满足，缺乏对已有思维的审视与拓展。教师是数学学习的引导者，可以通过提供新的学习材料，打开儿童的数学视野，让数学思考在新的空间驰骋。例如，特级教师俞正强执教拓展欣赏课《怎样求出地图的面积》，在学生十分困惑的情况下，教师抓住契机，让学生观摩问题解决的具体过程：（1）沿不规则边线剪下地图（如图2）；（2）把地图贴在一块较厚的纤维板上；（3）用细木锯沿边线锯下木板；（4）称出木板的重量并量出厚度；（5）在这种纤维板上锯一块体积为1立方厘米的木块，并称出重量；（6）算出锯下的木板的体积（总重量÷每立方厘米的重量）；（7）用体积除以厚度得出底面积。然后组织学生讨论“为什么我们没有想到这种解决方法”，学生经过反思，明确了“解决面积问题除了从平面图形角度思考，还可以从立体角度切入”，由此拓宽了学生的数学思考。

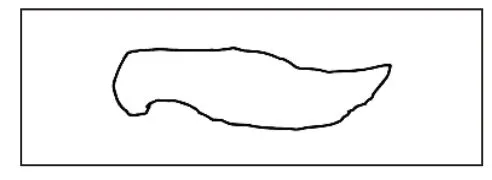
（图2）

3.寻根究底，通晓“为什么”，精深数学思考。

数学教学不仅要让儿童掌握基本的方法和规则，还要弄清来龙去脉，对方法和规则进行必要的解释与说明，通晓其存在的合理性，这样，儿童才能真正建构起对知识的理解。因此，教师教学时要抓住契机，进一步启发儿童展开数学思考，及时推进一步、深挖一尺。例如，教学苏教版六下《用方向和距离确定位置》一课，在学生掌握了用方向和距离描述位置的方法，并感受到用方向和距离确定位置的准确性之后，教师适时追问：“为什么用方向和距离可以准确确定物体的位置呢？”一石激起千层浪，学生产生了强烈的好奇心和求知欲，教师随即借助课件向学生展示了“面—线—点”逐步精确确定位置的过程，学生恍然大悟，获得了对确定位置方法的深度理解。之后，教师问及“空间内如何确定位置”时，学生提出“需要有类似的两条线交叉确定”，可见，学生已经勾勒出空间内的经线和纬线了。

（三）梳理知识脉络，织就数学思考的结点

由于儿童的个体理解不同，认知图式有时还不够清晰，甚至不准确。教学时，教师要注重引导儿童回顾、反思、对比、分析，梳理知识脉络，让其认知图式更清晰，为其后续展开新的学习之旅做好孕伏。

1.比较新旧学习方法，沟通联系。

教学时，教师要注重引导儿童通过对比梳理新旧学习方法之间的联系与区别，把握不同学习方法的要点和关键，促进他们形成结构性认识。仍以《圆的认识》一课的教学为例，在学生掌握了圆规画圆的方法，并欣赏了用直尺画圆以及固定线一端画圆的过程后，教师提出问题：“几种画圆方法有什么异同？”引导学生深入分析比较，从操作要领的具体感知到原理的洞察理解，使他们逐步领悟知识本质，即定点与定长是形成圆的基本条件，从而促进学生深入理解圆的概念，同时为其认识圆心、半径和直径做好铺垫。

2.解析学习过程，强化理解。

在学习过程中，儿童往往会更多地关注结果，而忽视知识展开的过程；会更多地关注对现象的感知，而忽视对本质的理解。因此，教师要注意引导儿童解构过程，抓住关键点进行剖析，强化儿童的数学理解。例如，教学苏教版三上《轴对称图形》一课，教师课件演示“将一张纸对折，画一画，剪一剪，做一个轴对称图形”，学生多关注做出轴对称图形的形状，而对方法与过程缺乏必要的思考。为此，教师及时引导学生反思操作步骤，适时点拨“对折”要求，并在学生操作后追问“为什么要将纸对折后再剪”，启发学生做后思，巩固对概念的理解与掌握。

3.感悟教学思想，提升认识。

数学思想是数学精神的内核，是儿童“带得走”的东西。但是，儿童不容易感悟到知识形成过程中蕴含的数学思想。因此，教师要对学习内容有学科理解和把握，在儿童数学思考过程中因势利导，帮助他们获得感悟、提升认识。例如，教学苏教版六下《圆柱的体积》一课，教师课件动态演示将圆柱32等分、64等分、128等分拼成近似的长方体，使学生感知到“等分的份数越多，拼成的物体越接近长方体”，如果无限等分下去可以拼成长方体。接着，教师启发学生反思：“圆柱体积计算推导过程‘似曾相识’，让你想到了什么？”引导学生将圆柱体积计算推导与圆的面积计算推导勾连起来，感悟其中蕴含的转化思想与极限思想。

综上所述，立足儿童的学习心理和内在需求，观照儿童的认知规律，拉进儿童与数学的距离，体现了学习的自然性和生动性。在教学中，教师要注意引导儿童理解数学，自然展开数学思考。