基于路面自适应的多轮轮毂电机驱动车辆驱动防滑控制

陈路明， 廖自力， 张征

(1.陆军装甲兵学院 兵器与控制系, 北京 100072; 2.国民核生化灾害防护国家重点实验室, 北京 102205)

0 引言

驱动力控制系统是一类较为典型的车辆行驶控制系统，这种系统一般以驱动防滑控制(ASR)为核心，在车辆起步、加速等行驶工况，对车轮滑转状态进行调整，改善车辆的动力性能和稳定性[1]。与传统汽车相比，轮毂电机驱动车辆各个执行器相互独立，可直接控制电机转矩输出，这类车辆在ASR系统设计方面具有一定的优势[2]。目前，国内外学者为电驱动车辆设计了很多种驱动力控制系统，大多数都采用了基于滑转率的控制方法[3-4]。文献[5]和文献[6]分别将模糊控制和自抗扰控制应用于车辆油门和制动控制器中，进行牵引力控制。为了提高驱动转矩控制的精度，文献[7]设计了一种基于滑模控制方法的驱动防滑系统，根据车辆单轮受力模型和滑动模态函数，推导了车轮防滑控制所需的驱动力等效控制量。这些系统大多面向4轮驱动的民用电动车辆，一般只能适应单一的道路环境，缺乏控制器对路面变化的适应性研究。实际上，与4轮驱动车辆相比，多轮轮毂电机驱动车辆的行驶工况通常更为恶劣，需要在低附着路面、变附着路面条件下保持良好的机动能力，有时还要面临急加速行驶，越野行驶等特殊工况[8]，因此需要根据多轮车辆结构配置和操纵性特点，设计具有路面自适应功能的控制系统。

道路识别的关键是路面附着系数估计，路面附着系数影响轮胎与道路之间的作用力，并决定车辆行驶的最佳滑转率[9]。路面识别方法可以分为两类：基于试验的方法和基于模型的方法[10-11]。基于试验的方法一般使用了光学和声学传感器，在良好的测试条件下具有较高精度，然而这些传感器的可靠性很容易受到驾驶条件和外部环境的影响[12]。基于模型方法通常依赖轮胎模型采用滤波方法估计车辆状态参数和路面附着系数，由于车辆行驶时影响滑转率计算精度的因素很多，提高抗干扰性和鲁棒性是基于模型方法研究的难点问题[13]。

本文设计了一种具有路面自适应功能的多轮轮毂电机驱动车辆ASR系统。用衰减记忆无迹卡尔曼滤波(FM-UKF)法[14]对路面附着系数进行估算，然后改进滑模控制(SMC)方法，设计模糊滑模控制(FSMC)器根据路面辨识结果进行ASR，使车辆在路面动态变化条件下也能具备较好地动力性和稳定性。最后，在基于dSPACE系统的实时仿真平台上设计不同工况的车辆行驶仿真实验。

1 车辆系统建模

1.1 非线性3自由度车辆模型

忽略空气阻力，将滚动阻力线性化处理，分别建立研究对象双轨3自由度车辆模型和车轮受力分析模型[15]，分别如图1和图2所示。图1中：v为车辆速度；vx、vy分别为车辆纵向速度、侧向速度；β为质心侧偏角；γ为横摆角速度；Fxil、Fxir分别为第i轴左、右两侧车轮纵向力，Fyil、Fyir分别为第i轴左、右两侧车轮侧向力，i=1,2,3,4；δil、δir分别为第i轴左、右两侧车轮转向角；αil、αir分别为第i轴左、右两侧车轮侧偏角；Ld为轮距；Li为第i轴与质心处的距离。图2中：m为车辆质量；g为重力加速度；ω为车轮轮速；Td为驱动力矩；Mf为滚动阻力矩；Fx为车轮纵向力；Fz为车轮垂直载荷。

图1 3自由度车辆模型Fig.1 3-DOF dynamics model of vehicle

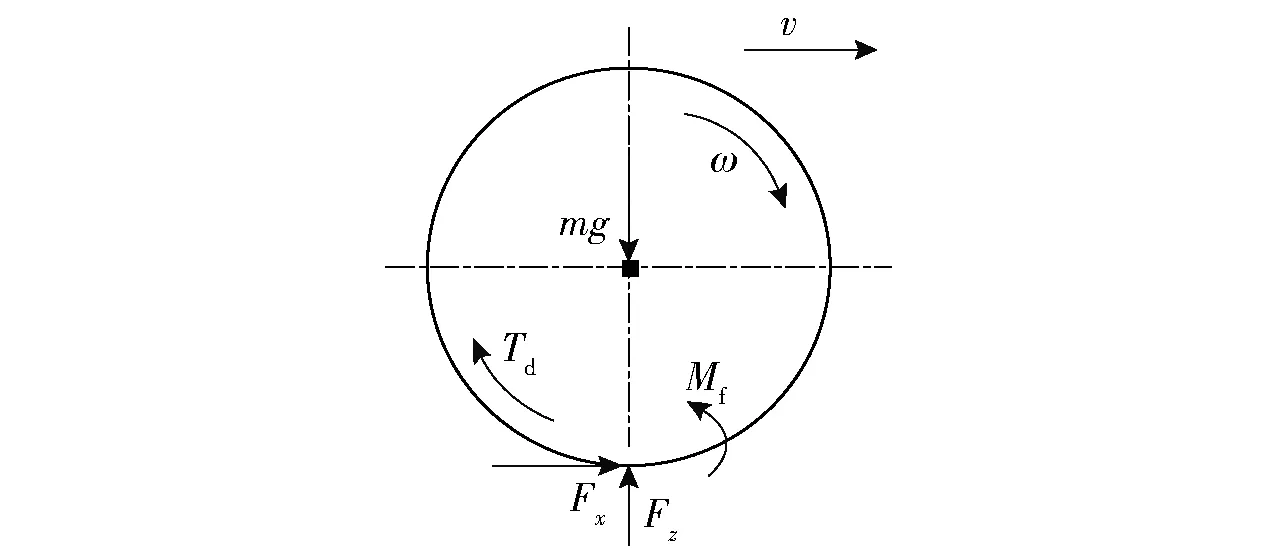
图2 车轮受力图Fig.2 Wheel force analysis

根据车辆动力学，平衡方程为

max=-Fy1lsinδ1l+Fx1lcosδ1l-Fy1rsinδ1r+
Fx1rcosδ1r-Fy2lsinδ2l+Fx2lcosδ2l-
Fy2rsinδ2r+Fx2rcosδ2r+Fx3l+Fx3r+Fx4l+Fx4r，

(1)

may=Fy1lcosδ1l+Fx1lsinδ1l+Fy1rcosδ1r+
Fx1rsinδ1r+Fy2lcosδ2l+Fx2lsinδ2l+
Fy2rcosδ2r+Fx2rsinδ2r+Fy3l+Fy3r+Fy4l+Fy4r，

(2)

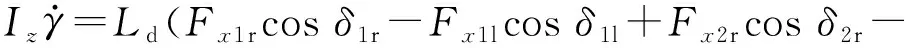
(3)

式中：ax、ay分别为车辆纵向加速度、侧向加速度；Iz为横摆转动惯量。

1.2 车轮受力模型

车轮力矩表达式为

(4)

Td=icTe，

(5)

Mf=fgFzR，

(6)

式中：I为车轮转动惯量；R为车轮有效半径；ic为减速器传动比；Te为轮毂电机转矩；fg为滚动阻力系数。

1.3 轮胎模型

Dugoff轮胎模型能够描述车辆非线性特性，并且计算简便，选用Dugoff轮胎模型作为ASR的轮胎模型，其表达式为

(7)

(8)

(9)

(10)

式中：Fy为车轮侧向力；μ为路面附着系数；Cx、Cy分别表示纵向刚度、侧偏刚度；S为滑转率；f(ψ)为Dugoff轮胎模型的修正系数；ψ为表征轮胎力非线性特征边界值；к为速度影响因子，与轮胎结构及材料有关，作用在于修正轮胎滑移速度对轮胎力的影响。

归一化后，有

(11)

各轮侧偏角近似表达式为

(12)

2 路面识别方法设计

2.1 状态估计模型

构建状态方程和量测方程：

(13)

式中：Xk+1和Xk分别为第k和第k+1时刻状态变量；g(·)和h(·)分别为状态方程中的非线性函数和观测函数；u为输入向量；wk、vk均为噪声；Yk为第k时刻量测变量。

状态变量为

X=[μ1l,μ1r,μ2l,μ2r,μ3l,μ3r,μ4l,μ4r]T.

(14)

输入向量为

u=[δ1l,δ1r,δ2l,δ2r]T.

(15)

量测变量为

Y=[ax,ay,γ]T.

(16)

根据车辆动力学，得

(17)

(18)

(19)

2.2 无迹卡尔曼滤波方法设计

(20)

2n+1个sigma点权值为

(21)

初始条件为

(22)

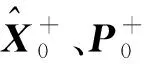
对状态变量进行无迹变换，得到sigma点预测值，即

(23)

sigma点预测值加权后得到

(24)

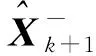
(25)

(26)

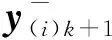
(27)

计算量测量协方差

(28)

式中：Rc为量测噪声协方差。

X与Y协方差可表示为

(29)

Kalman滤波增益为

Kk+1=P(Y,Y)[P(X,Y)]-1.

(30)

更新得

(31)

2.3 FM-UKF估计方法设计

传统无迹卡尔曼滤波(UKF)法是一种无限增长记忆滤波方法，这种方法非常容易受到模型精度的影响，导致滤波误差激增甚至发散等现象[16]。因此，引入指数衰减记忆因子，设计FM-UKF法修正估计值误差。

取k-i=N，则第N时刻Kalman滤波增益为KN，在UKF法基础上进行改进，为尽量减弱UKF法旧时刻量测值在状态变量估计中的作用，降低N时刻以前的Kk-i值权重，加强新时刻量测值对估计方法的修正作用，突出N时刻的KN值。基于指数加权的方法，引入指数衰减忘记因子epi，其中指数表达式为

(32)

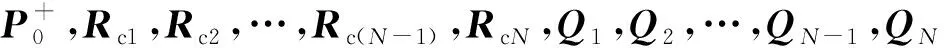
(33)

3 基于FSMC的ASR系统设计

轮胎滑转率与路面附着系数之间存在密切关系，如图3所示。由图3可以看出，附着系数一般先随滑转率增加而增加，达到峰值后再减小。路面附着系数峰值对应的滑转率即为最佳滑转率。

图3 路面附着系数与滑转率关系曲线Fig.3 Curve of relationship between road adhesion coefficient and slip ratio

实际行驶时路面总是容易变化，因此根据FM-UKF法的路面辨识结果和轮胎滑转率与路面附着系数曲线预估当前路面最佳滑转率，然后设计模糊滑模ASR器，对打滑车轮轮毂电机输出转矩进行调节，尽可能减小轮胎滑转率与最佳滑转率的差值。

当车辆处于驱动工况时，理论纵向滑转率S*与实际纵向滑移率S的关系为

(34)

定义滑转率差值：

e=S*-Sb，

(35)

式中：Sb为最佳滑转率。

对(35)式求导，得

(36)

SMC的滑模面为

(37)

式中：c为滑模面系数。

根据(35)式～(37)式，得

(38)

式中：ε为趋近速率，且ε>0；Ω为滑模边界值，且Ω>0.

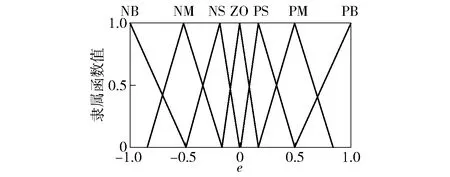
图4 e的隶属函数Fig.4 Membership function of input e

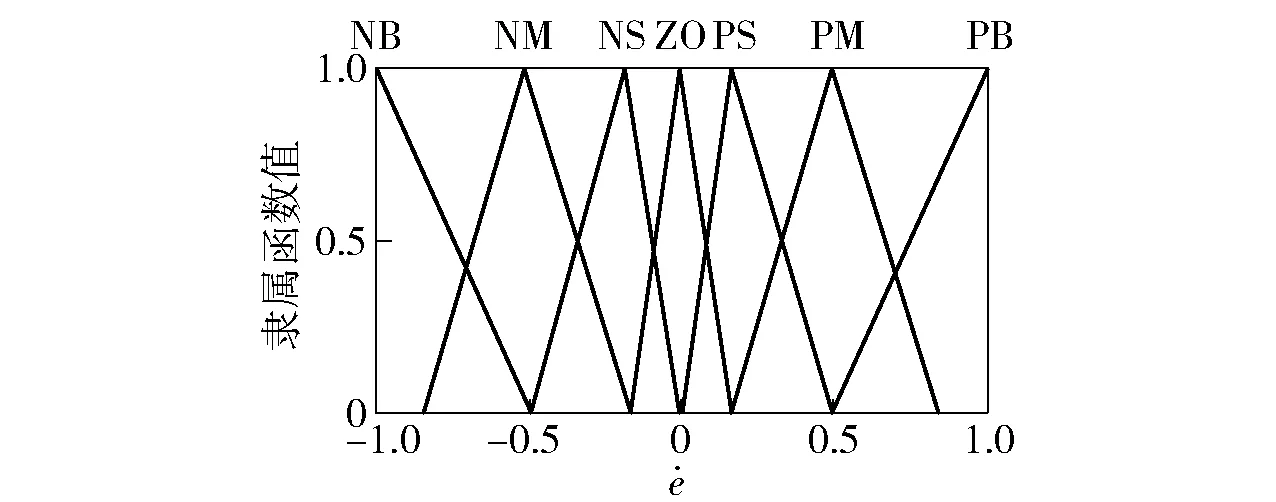
图5 的隶属函数Fig.5 Membership function of input

图6 ε的隶属函数Fig.6 Membership function of output ε

图7 ε的三维映射图Fig.7 Three-dimensional map of output ε

根据(10)式、(34)式和(38)式得

(39)

对(4)式求导，得

(40)

(39)式代入(40)式，根据所研究车辆的轮毂电机模型[18]，得到模糊滑模控制输出的调节力矩，从而实现车辆ASR.

4 仿真结果及分析

在如图8和图9所示实时仿真平台进行实验，检验路面识别和ASR的效果。

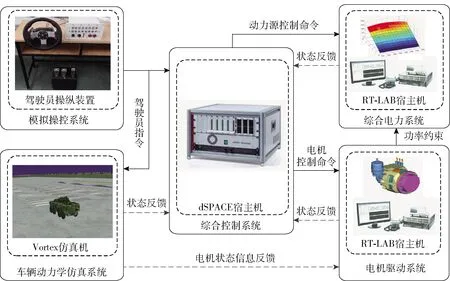
图8 仿真平台子系统信息交互Fig.8 Information interaction among subsystems of simulation platform

图9 实时仿真平台Fig.9 Overall structure of simulation platform

实验采用的仿真实验平台主要由驾驶员模拟操控系统、基于Vortex(加拿大CM-LABS公司生产的一款多体动力学模拟仿真系统)的动力学仿真系统、基于RT-LAB(加拿大Opal-RT公司生产的一款工业级实时仿真系统)的综合电力系统、基于RT-LAB的电机驱动系统和基于dSPACE(德国dSPACE公司开发的一套实时仿真系统)的综合控制系统构成，各系统间采用Flexray总线通信。车辆主要参数如表1所示。

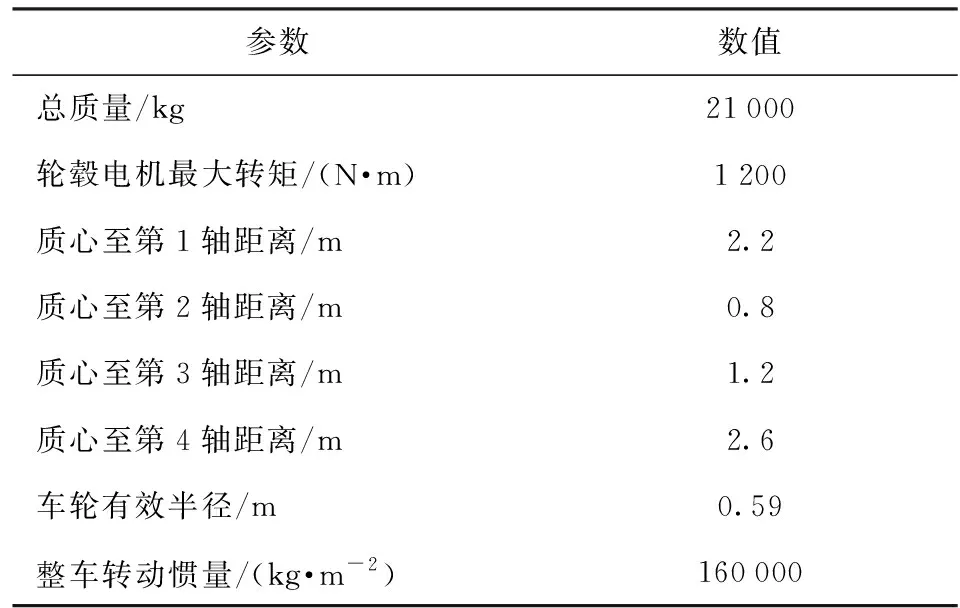
表1 车辆部分参数Tab.1 Parameters of vehicle

4.1 路面附着系数估计实验

为了验证不同环境和驾驶条件下的路面附着系数估计效果，设计了一般路面(μ=0.5)双移线行驶实验和变附着系数路面连续转向行驶实验，仿真结果如表2、图10～图13所示。

由表2及图10～图13可以看出，不同环境和驾驶条件下，FM-UKF法的估计值与其实际值都基本吻合，估计精度优于UKF法。

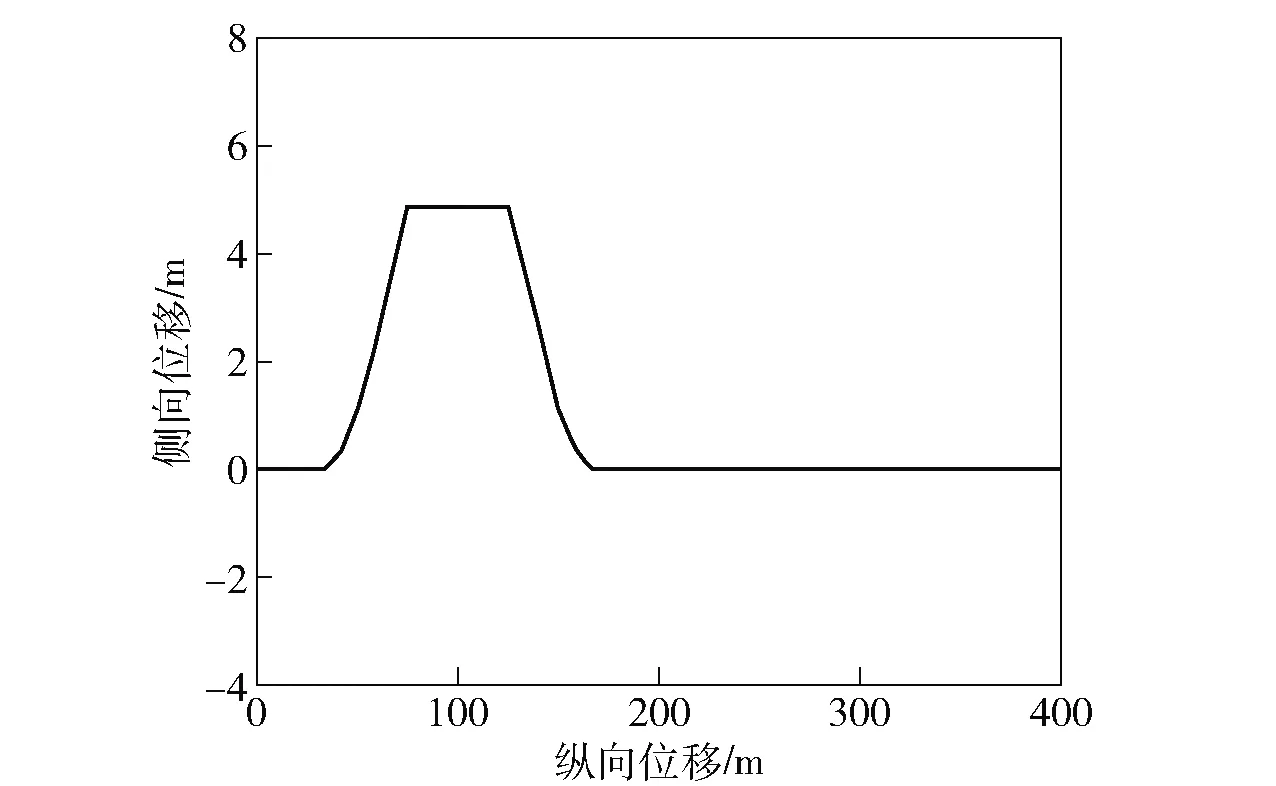
图10 双移线行驶的期望路径Fig.10 Expected path on double lane

图11 双移线行驶路面附着系数估计Fig.11 Road adhesion coefficient estimation for double lane change driving

图12 连续转向行驶的方向盘转角Fig.12 Steering wheel angle for continuous steering

图13 连续转向行驶路面附着系数估计Fig.13 Road adhesion coefficient estimation for continuous steering

表2 路面附着系数估算误差统计Tab.2 Estimated error statistics of road adhesion coefficients

4.2 ASR实验

为了验证控制策略在不同行驶工况下的驱动力控制效果，设计了表3所示3种典型道路实验。

4.2.1 低附着系数路面行驶实验

依照表3中实验工况1设置仿真条件，选取路面附着系数估算误差的平均绝对误差和均方根误差作为评价指标，不同估计方法的误差结果如表4所示，部分关键过程参数如图14～图16所示。

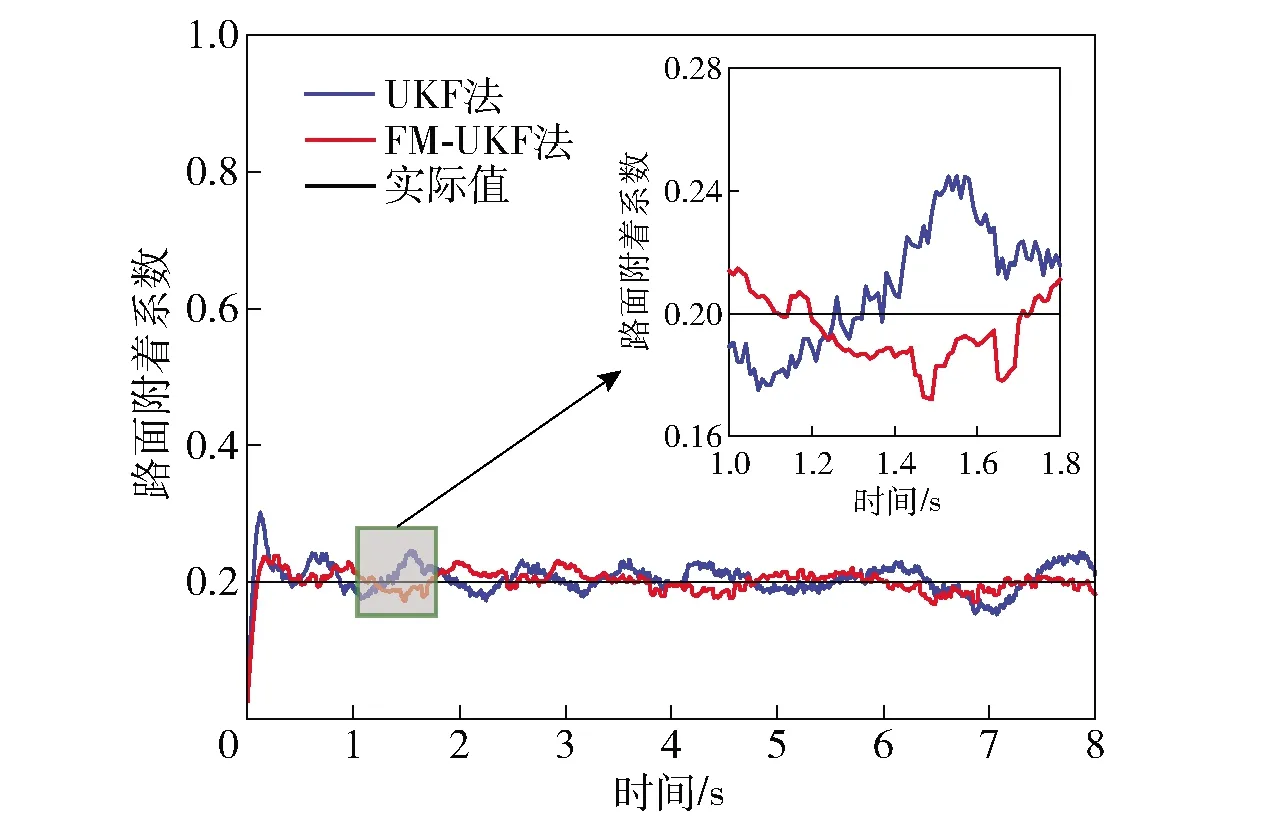
图14 工况1的路面附着系数估算对比Fig.14 Road adhesion coefficient estimation under Condition 1

图15 工况1的车速与轮边速度Fig.15 Vehicle speed and wheel speed under Condition 1

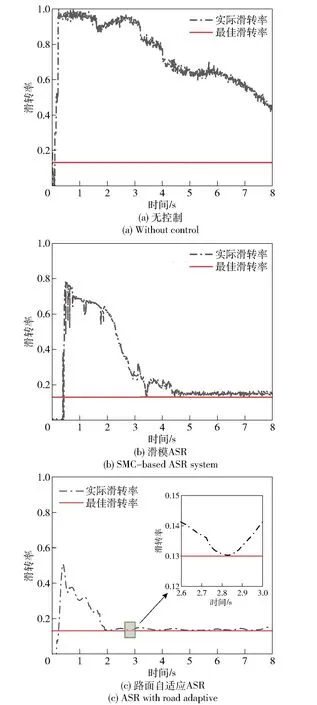
图16 工况1的车轮滑转率Fig.16 Slip ratio under Condition 1

表3 ASR实验条件设置Tab.3 Simulation conditions of ASR

由表4和图14可知，UKF法和FM-UKF法都能对单一道路的路面附着系数进行有效估计，但FM-UKF法具有更高的估计精度。由图15可以看出，当车辆未施加驱动力控制时，轮胎打滑严重，轮边速度迅速增加，整个行驶过程中轮边速度明显高于车速。基于SMC的ASR系统有效减小了轮边速度与车速之间的差异，驱动轮打滑现象得到了一定程度的抑制。而采用路面自适应ASR后，车轮打滑情况得到了更快、更明显的抑制，加速过程中未出现过度滑转现象，轮边速度和车速大致接近。另外与无驱动力控制状态相比(加速至43 km/h)，施加控制后，车辆在相同时间内加速至52 km/h，动力学性能得到了提高。

表4 低附着系数路面估算误差统计Tab.4 Estimated error statistics of low-adhesion road

由图16(a)可知，当车辆不受驱动力控制时，驱动轮实际滑移率与当前道路最佳滑移率相差较大，起步阶段平均滑转率误差大于85%，严重影响车辆动力性能。图16(b)表明，在驱动轮发生严重打滑时，基于SMC的ASR系统对轮胎滑转率进行了控制，实际滑转率在最佳滑转率附近波动，但平均误差较大，并且出现一定程度的抖振现象。从图16(c)可以看出，采用路面自适应ASR后，实际滑转率更加趋近于最佳滑转率，并且改善了传统滑模控制的抖振问题，控制效果更加明显。

4.2.2 对开路面行驶实验

依照表3中的实验工况2设置仿真条件，实验结果如表5及图17～图21所示。

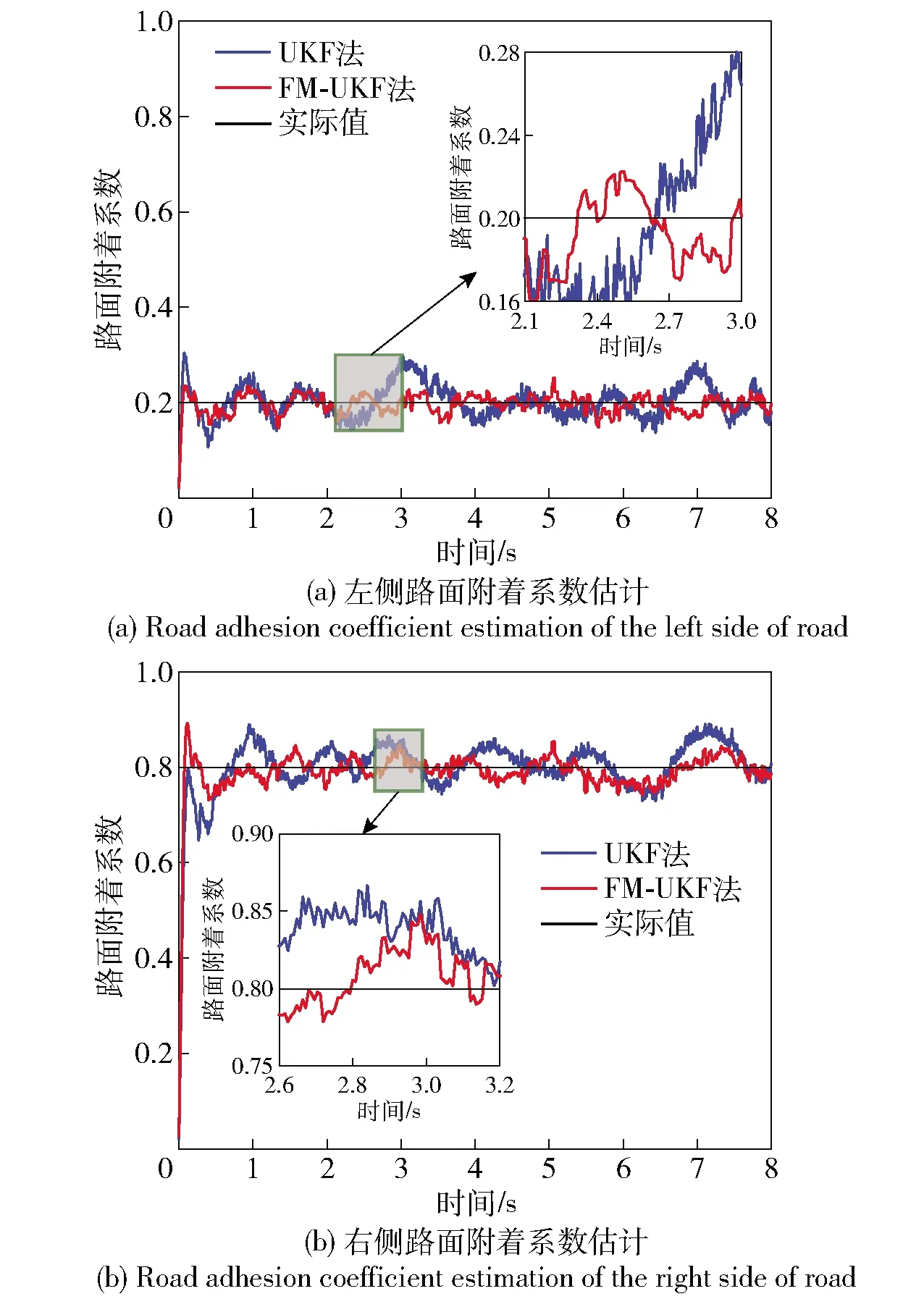
图17 工况2的路面附着系数估算对比Fig.17 Road adhesion coefficient estimation under Condition 2

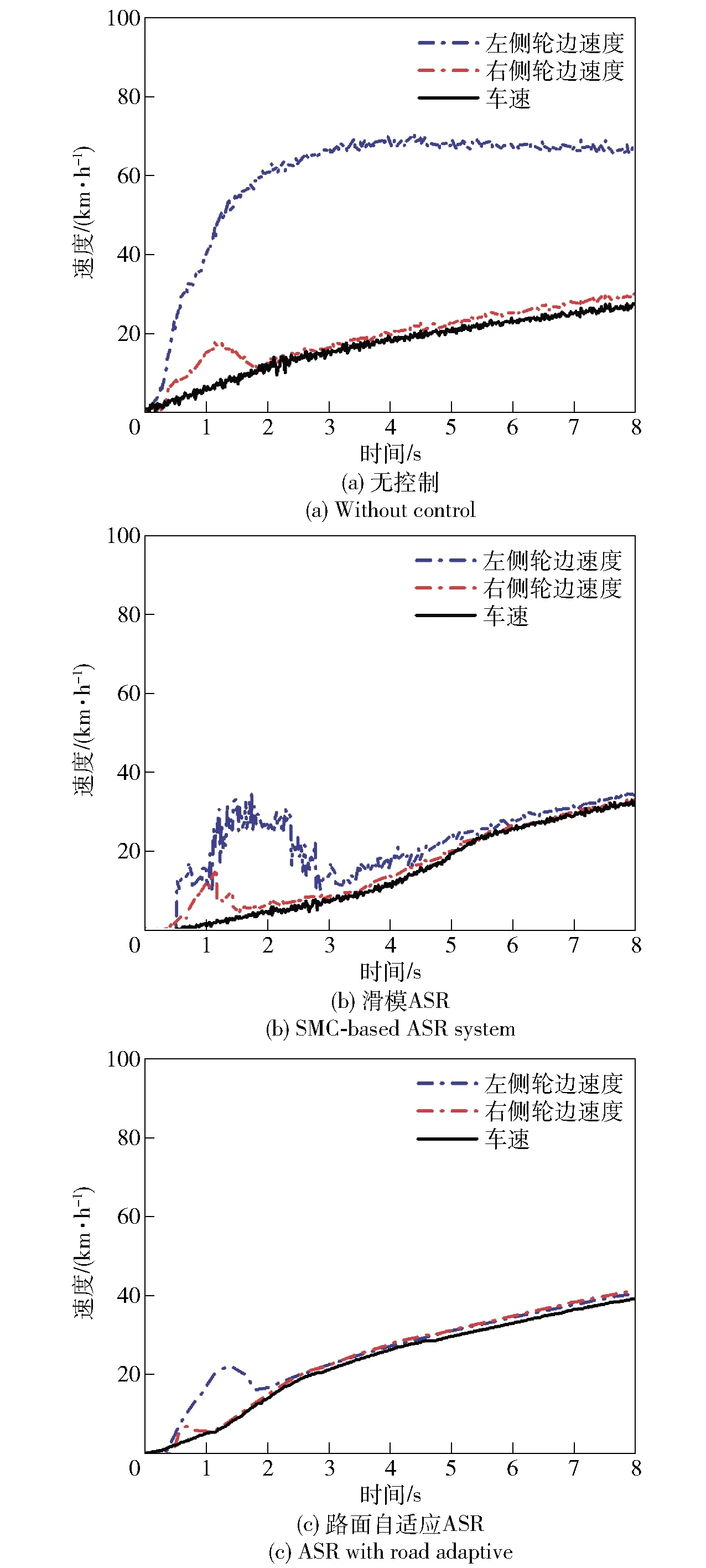
图18 工况2的车速与轮边速度Fig.18 Vehicle speed and wheel speed under Condition 2

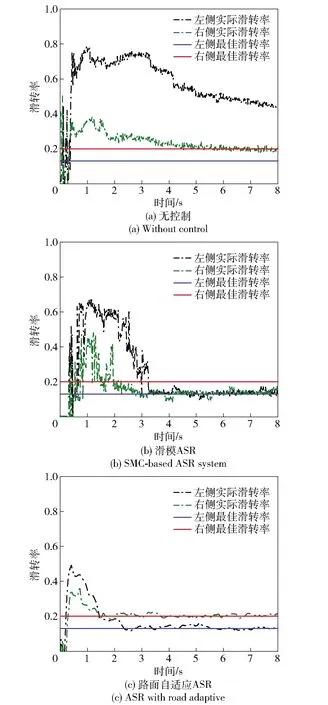
图19 工况2的车轮滑转率Fig.19 Slip ratio under Condition 2

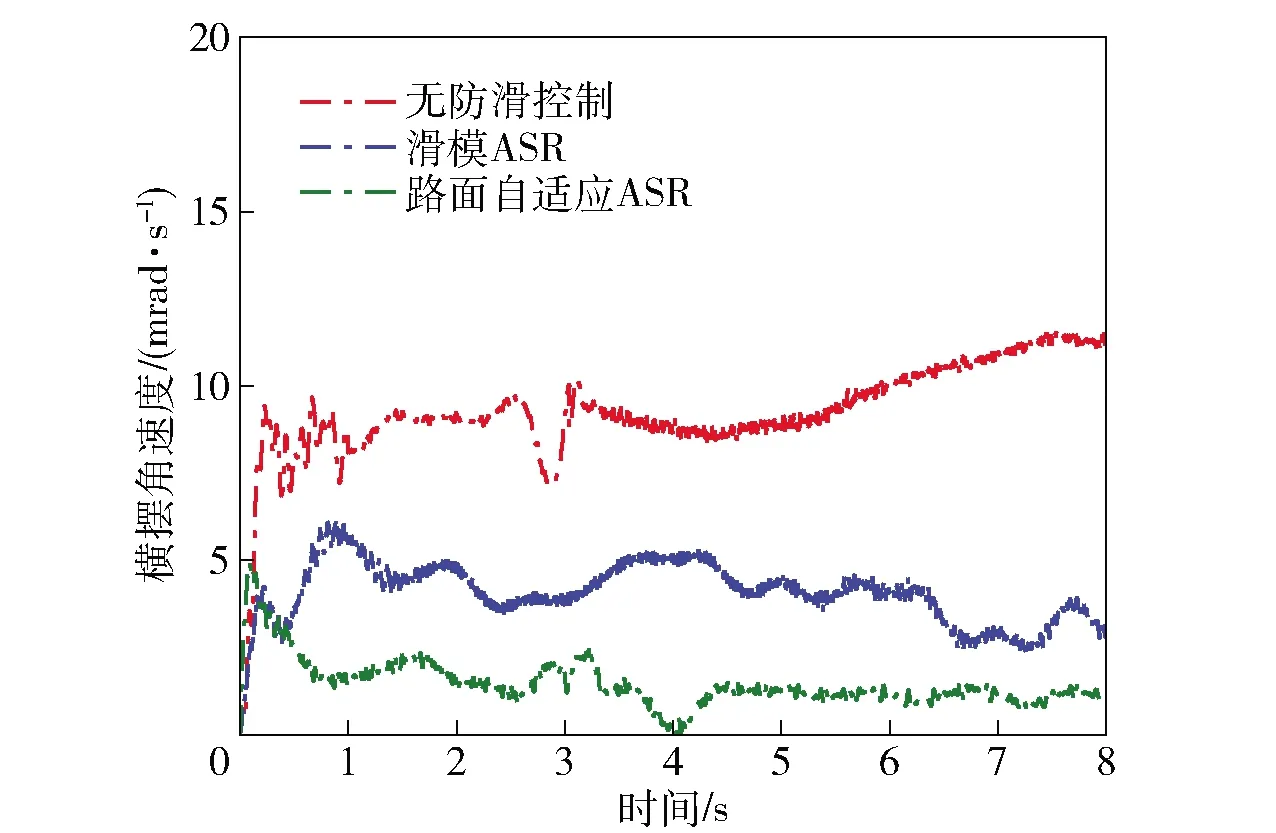
图20 对开路面车辆横摆角速度Fig.20 Yaw rate of vehicle on μ-split road

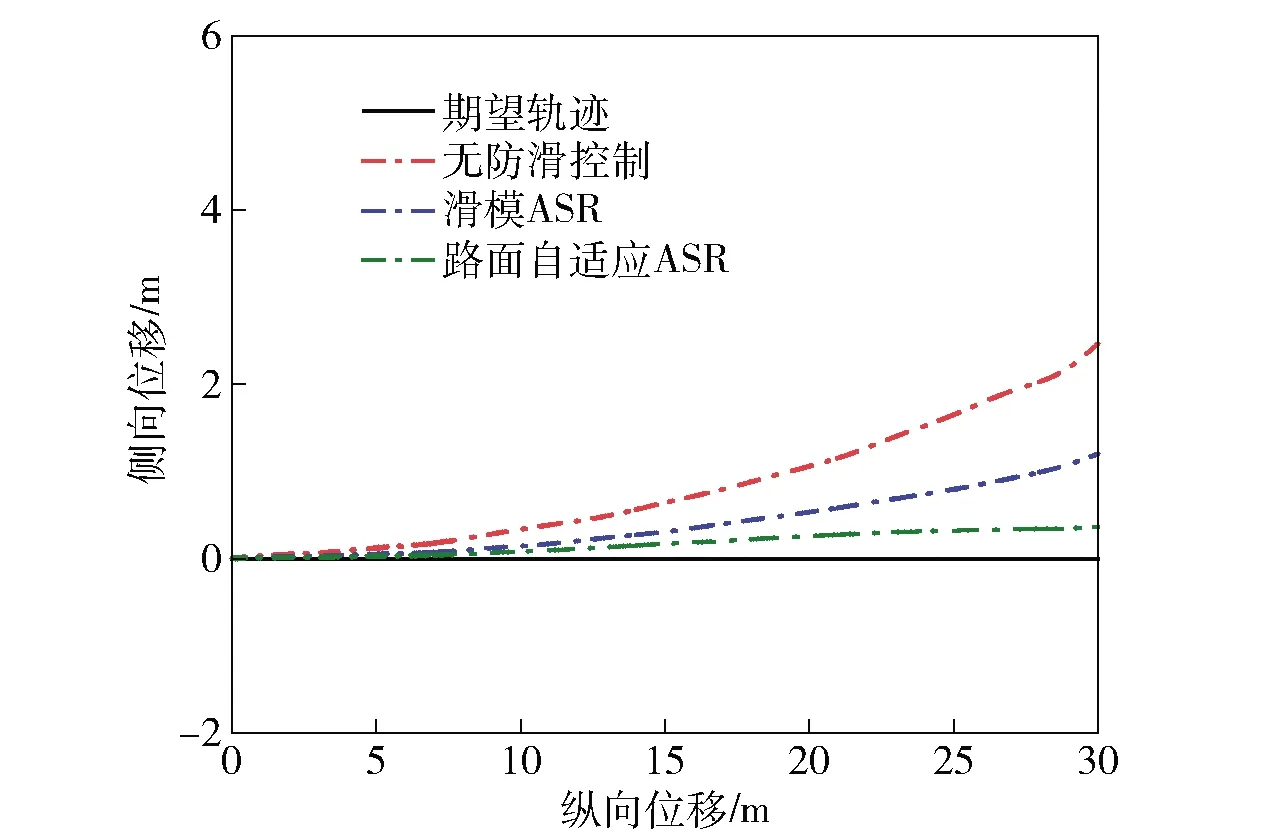
图21 对开路面车辆运行轨迹Fig.21 Vehicle track on μ-split road

表5和图17表明，与UKF法相比，FM-UKF法更能准确识别左右两侧路面附着系数的差异，FM-UKF法估计值更接近实际值。由图18可以看出，当两侧路面附着系数不同时，无驱动力控制的车辆左右侧车轮轮边速度差异很大：左轮在低附着系数路面上运动，打滑现象比较明显，轮边速度迅速增加；而右轮在相对良好的路面上行驶，打滑现象相对较轻，轮边速度较为平稳地增加。采用基于SMC的ASR系统后，驱动轮过度打滑现象得到了控制，车辆两侧轮边速度的差异变小。路面自适应驱动防滑控制系统则根据路面识别结果分别对两侧车轮的轮边速度进行了有效调整。

表5 对开路面估算误差统计Tab.5 Estimated error statistics of μ-split road

由图19可知，对于未施加驱动力控制的车辆，左右侧车轮实际滑移率相差很大：左侧路面条件较差，车轮实际滑转率明显高于最佳优滑转率；而右侧路面条件较好，虽然车辆起步时打滑较为严重，但整体趋势上右侧车轮滑转率与最佳滑转率间的误差较小。采用基于SMC的ASR系统后，两侧车轮打滑现象均得到了一定的抑制，但这种系统不能根据对开路面特点对两侧车轮滑转率进行不同地调整，并且系统波动较大，控制效果不太稳定。路面自适应ASR系统在车辆行驶过程中准确识别了两侧路面附着系数差异，根据路况合理减小两侧车轮滑转率与相应最佳滑转率的偏差，有效提高了车辆驱动能力，另外采用路面自适应ASR系统的车辆动态参数波动较小，控制效果较好。

图20和图21表明，在对开路面加速时，无驱动力控制状态下车辆最大横摆角速度达到11 mrad/s左右，侧向位移持续增大到2.49 m，出现了行驶轨迹偏离现象，严重影响了车辆操纵稳定性。基于SMC的ASR系统和路面自适应ASR系统都对车辆进行了行驶控制，基于SMC的ASR系统使车辆最大横摆角速度减小至7 mrad/s，侧向位移约为1.23 m.路面自适应ASR系统使车辆最大横摆角速低于4 mrad/s，侧向位移小于0.5 m.

4.2.3 对接路面行驶实验

依照表3中的实验工况3设置仿真条件，实验结果如表6、图22及图23所示。

表6 对接路面估算误差统计Tab.6 Estimation error statistics of docking road

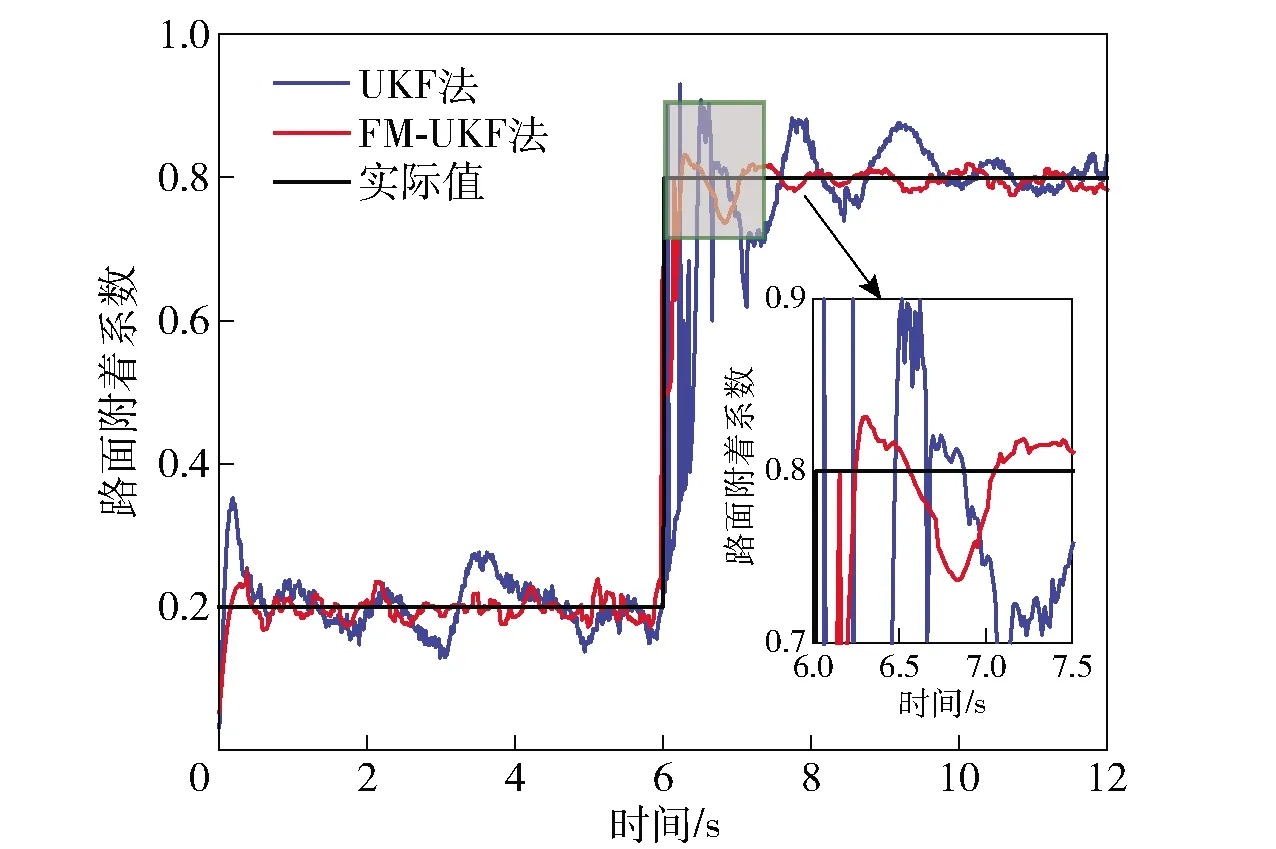
图22 工况3的路面附着系数估算对比Fig.22 Road adhesion coefficient estimation under Condition 3

图23 工况3的车轮滑转率Fig.23 Slip ratio under Condition 3

表6及图22结果表明，当行驶路况突然变化时，UKF法的路面附着系数估计值与实际值具有较大差异，而FM-UKF法的估计值依然非常准确地跟踪实际值，这说明了FM-UKF法在对接路面上具有更好的估计效果。

从图23(a)可以看出，在对接路面加速行驶时，未施加驱动力控制车辆驱动轮打滑现象非常明显，实际滑转率与最佳滑转率的偏差很大，路面附着系数发生变化时，轮胎滑转率出现明显抖动，车辆动力性能和稳定性能较差。图23(b)表明：滑模驱动防滑系统对改善驱动轮过度打滑现象具有一定的作用，减小了滑移率与最佳滑移率之间的差异，但系统无法识别道路突变，只能设定固定的最佳滑移率进行控制；此外，由于传统滑模控制的特点，系统抖振现象明显，影响了控制效果。图23(c)表明，路面自适应ASR系统能够快速感知路面附着系数的变化，并根据道路状况及时调整最佳滑移率进行ASR，系统具有更小的抖动和更好的稳定性。

5 结论

本文针对多轮轮毂电机驱动车辆，进行车辆系统建模，采用FM-UKF法对行驶路面进行了辨识，实现路面附着系数的实时、准确估计。在路面识别的基础上，实时确定当前道路最佳滑转率，解决传统ASR系统采用固定最佳滑转率进行控制的问题，设计驱动力模糊滑模控制器，调整滑转率与最佳滑转率的偏差。基于dSPACE系统，进行了实时仿真实验。得出以下主要结论：

1) FM-UKF法准确辨识了行驶路面的差异和跃变，响应迅速、鲁棒性强。

2) 路面自适应ASR系统实现了路面自适应功能，具有较好地ASR效果：在低附着系数路面上，模糊滑模控制器迅速将实际滑转率控制在最佳滑转率间附近；在对开路面，依据左右侧最佳滑转率分别对两侧车轮施加驱动力控制，有效减小了滑转率误差；在对接路面，根据路面附着系数变化，对实际滑转率进行了控制，较好地满足了电驱动车辆在不同环境下的行驶需求。