分布式电驱动车辆极限越野环境下高速避障与稳定性控制

刘聪， 刘辉,2， 韩立金,2， 陈科

(1.北京理工大学 机械与车辆学院, 北京 100081; 2.北京理工大学 前沿技术研究院, 山东 济南 250300;3.内蒙古第一机械集团股份有限公司， 内蒙古 包头 014032)

0 引言

相比搭载发动机的机械传动车辆，分布式电驱动车辆具有各轮驱动力矩独立可控、驱动电机响应迅速以及转速、转矩可精确测量等优势，特别是在车辆底盘动力学控制方面，具有很大的发展潜能[1]。分布式电驱动车辆凭借其高机动性以及高冗余性的优势，可高速且灵活躲避障碍物，具有快速突击能力和操纵稳定性能，广泛应用于民用和军事领域[2]。

为推进分布式电驱动车辆的快速发展，许多学者针对提高其操纵稳定性和机动性两方面进行了相关研究[3-4]。Jin等[5]提出一种基于线性变参数技术的分布式驱动电动汽车横向稳定性鲁棒增益调度控制器，具有高效的跟踪性能和对不确定性的较强鲁棒性。为提高车辆在极限工况下的横向稳定性， Chen等[6]提出一种基于2阶滑模控制和非线性干扰观测器相结合的自主4轮独立驱动电动汽车路径跟踪和稳定性控制方法，对不确定性干扰具有良好的鲁棒性。Li等[7]提出一种极限工况下基于模型预测控制理论的车辆纵向、横向协调稳定性控制器方法，解决轮胎力在高度非线性情况下车辆横向、纵向运动的耦合问题。为提高分布式驱动车辆低速转向机动性和高速行驶稳定性，胡金芳等[8]提出一种适应车速变化的4轮转矩分配策略。此外，刘聪等[9]提出一种基于转向状态预测的稳定性分层控制策略，可避免车辆在紧急避障过程中因时间延迟或是驾驶员反应不及时而引起的车辆失稳。祁炳楠等[10]提出一种基于能量法的分布式驱动电动车辆防侧翻稳定性控制策略，通过主动分配两侧驱动力矩来有效抑制整车侧倾运动。王伟达等[11]提出一种基于非线性联合滑模变结构的4轮独立驱动电动车横向稳定性控制策略，其可提高极限工况下车辆的操纵稳定性。谢伟东等[12]提出一种基于最优转矩矢量控制的分布式驱动车辆侧向稳定性控制系统。针对双侧独立电驱动履带车辆的行驶稳定性问题，张杰等[13]提出一种解耦和预测控制方法，可对纵向车速和横摆角速度进行解耦及独立控制。李胜琴等[14]提出一种基于滑模控制理论及罚函数法的分布式驱动电动汽车横摆稳定性控制策略。Zhou等[15]提出一种基于非线性模型预测控制(NMPC)的横向、纵向协调控制方法。Peng等[16]为实现4轮自主电机独立驱动电动汽车的协调路径跟踪和直接横摆力矩控制，提出一种具有有限时域的鲁棒模型预测控制(MPC)。然而，当前研究成果仅基于单一且传统的2自由度车辆动力学模型来设计分布式电驱动车辆的横摆力矩控制器，极限失稳情况下车身姿态修正无法达到精确控制，不能充分发挥4轮独立可控的独特优势。因此，构建一种适用于分布式电驱动车辆的横摆运动动力学方程是必要的。

本文针对分布式电驱动越野车极限环境避障过程中的路径保持和横向稳定性方面进行研究。为解决车辆在大幅度侧滑、甩尾等失稳情况下很难依靠质心横摆力矩控制来即时修正车身姿态的问题，提出一种协同考虑质心处和后轴中心处车辆状态信息的避障横向稳定性控制方法，细化了分布式电驱动车辆的横摆运动模型，构建一种新颖的双层融合型横摆运动车辆动力学方程。综合考虑越野环境中车辆系统非线性、时变性以及控制约束等性能指标，提出一种基于数据驱动多模型测控制的横摆、侧倾稳定性分层协调控制方法。

1 分层协调横向稳定性控制器结构

本文所提出的分布式电驱动车辆分层协调横向稳定性控制器结构图如图1所示，整个控制系统分为上、下两层结构，上层控制器为横摆、侧倾力矩集成控制，下层为4轮驱动转矩协调控制。图1中，Mz为融合型横摆力矩，δf为前轮转角，T1、T2、T3、T4分别为下层控制器预分配的左前电机转矩值、右前电机转矩值、左后电机转矩值、右后电机转矩值。

图1 分层协调稳定性控制器框架Fig.1 Hierarchical coordinated stability controller framework

2 车辆动力学模型构建

2.1 传统横摆运动动力学模型

本文主要研究分布式电驱动车辆二维平面内的横向动力学运动，仅需考虑纵向运动、侧向运动、横摆运动以及4个车轮转动的7自由度车辆动力学模型，如图2所示。图2中，Oxyz为车体坐标系，L为轴距，a、b为分别为质心到前轴、后轴的轴距，β为质心侧偏角，ωrc为车辆绕质心处的横摆角速度，v为车辆质心速度，vx为车辆的纵向速度，vy为车辆的侧向速度，Fxi(i=1,2,3,4)为各车轮所受纵向力，Fyi为各车轮所受侧向力，αf、αr分别为前轮胎、后轮胎侧偏角。

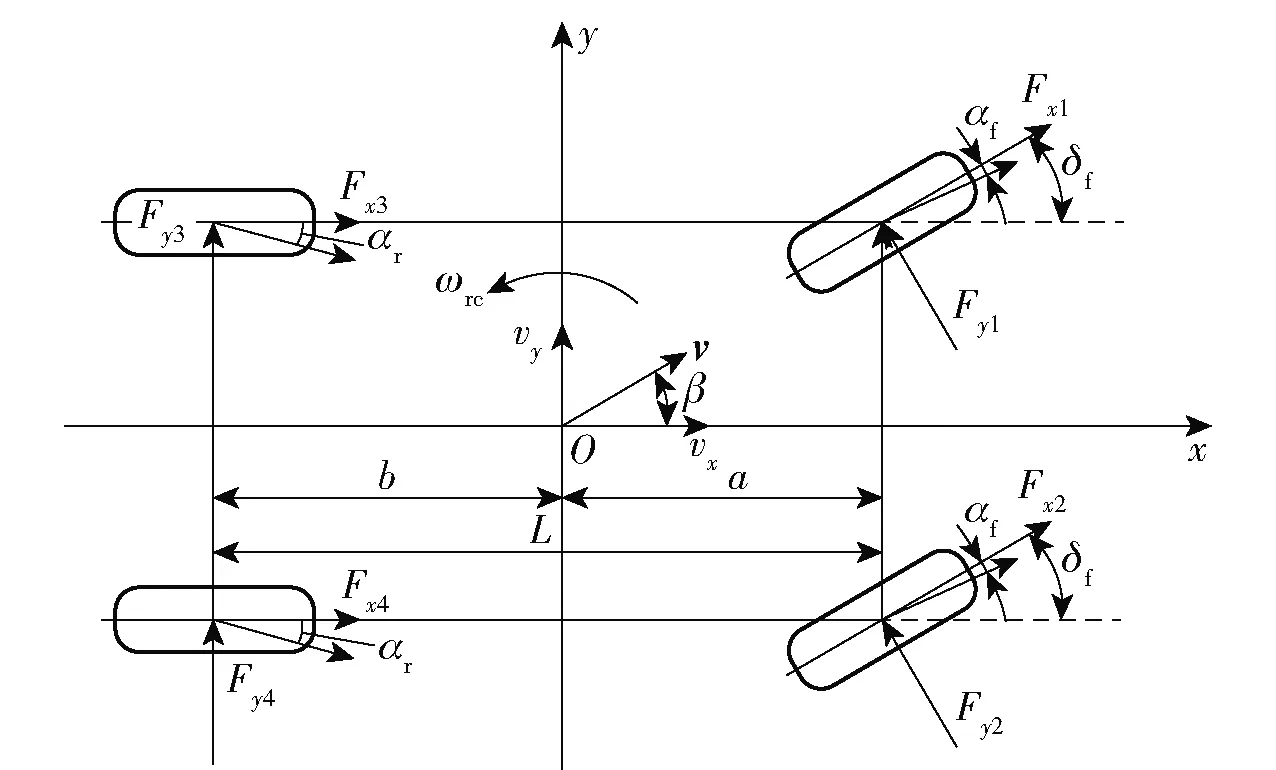
图2 7自由度模型Fig.2 7-DOF model

7自由度的运动微分方程如下。

纵向动力学方程为

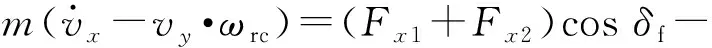
(1)

侧向动力学方程为

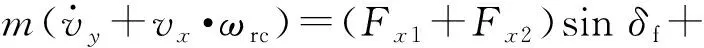
(2)

绕质心位置的横摆运动方程为

(3)

车轮的转动方程为

(4)

式中：m为整车质量；Iz为车辆绕z轴的转动惯量；B为前轴、后轴轮距(本文假设二者相等)；Jw为车轮转动惯量；ωi为车轮角速度；Ti为轮毂电机转矩；r为车轮滚动半径。

常规的横摆运动控制方式为基于车辆质心位置的横摆力矩控制，其可以保证车辆在小范围内失稳情况下的横向稳定性[17]。绕质心做横摆运动的2自由度车辆动力学微分方程为

(5)

2.2 双层融合型横摆运动动力学模型

当车辆由于大幅度侧滑甩尾而发生失稳时，后轴中心位置首先偏离期望轨迹。当偏离程度较为严重时，车辆最理想的横摆运动中心位置出现漂移现象，逐渐向前轴中心位置逼近，传统的仅考虑质心位置的横摆力矩控制方式已无法满足极限工况下的车身姿态修正需求。为解决以上问题，本文构建了一种双层融合型横摆运动动力学模型，其中所构建的绕前轴中心位置的横摆运动方程为

(6)

式中：Izf为绕前轴中心的转动惯量；ωrf为绕前轴中心的横摆角速度。

考虑到绕前轴中心的横摆运动，控制系统需要优先计算用于稳定后轴中心轨迹偏离程度的附加横摆力矩Mzf，所构建的绕前轴中心的横摆角速度微分方程为

(7)

式中：C3为左后轮的侧偏刚度；C4为右后轮的侧偏刚度。

通过以上分析，得到两种控制模式下的双层横摆角速度方程组表达式为

(8)

式中：C1、C2分别为左前轮侧偏刚度和右前轮侧偏刚度。为提高车辆的路径保持能力，需要保证车辆自身位置坐标实时维持在期望坐标附近。本文同时考虑了车辆质心位置和后轴中心位置偏离期望坐标点的程度，提高车辆横摆力矩控制的时效性。

车辆质心坐标位置计算公式为

(9)

式中：Ψ为车辆的航向角。后轴中心坐标位置计算公式为

(10)

根据轮胎侧偏特性，可得轮胎的纵向力表达式为

(11)

式中：Fxf、Fxr分别为前轮、后轮纵向力；Clf、Clr分别为前轮、后轮胎纵向刚度；sf、sr分别为前轮、后轮胎滑移率。

轮胎侧向力表达式为

(12)

式中：Fyf、Fyr分别为前轮、后轮胎侧向力。

轮胎滑动率s的表达式为

(13)

式中：ω为车轮转速。

综上所述，车辆在极限越野工况下进行避障时一般存在两种横向失稳的情况：一种失稳情况为小范围侧滑失稳，可通过基于质心处附加横摆力矩控制保证车辆转向稳定；另一种失稳情况为后车身大范围甩尾侧滑，轮胎力处于非线性工作区域，常规控制方式已无法即时修正车辆姿态。

本文针对分布式电驱动车辆4轮独立可控的独特优势，提出一种新颖的双层横摆角速度表达式，融合质心处和前轴中心处的两种横摆运动模式，可基于当前车辆的失稳程度分时调整当前横摆运动的最佳控制模式，从而实现4个驱动轮的驱动力矩即时且精确地修正当前车身失稳姿态，运动控制方式如图3所示。

图3 两种横摆运动控制模式Fig.3 Two yaw motion control modes

考虑到车身两处横摆力矩同时控制中存在耦合问题，并且增大控制器计算复杂度。为解决以上问题，本文分别将两处的横摆角速度观测值和附加横摆力矩控制量合理地融合在质心位置，如(14)式和(15)式所示。

融合型横摆角速度表达式为

(14)

融合型横摆力矩表达式为

(15)

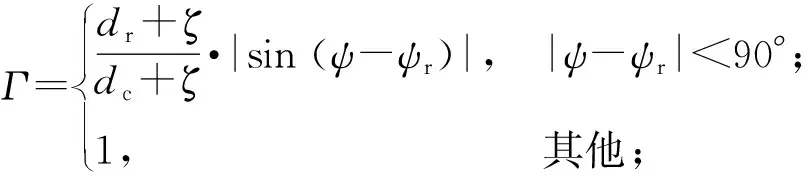
2.3 横摆、侧倾协调运动动力学模型

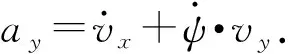
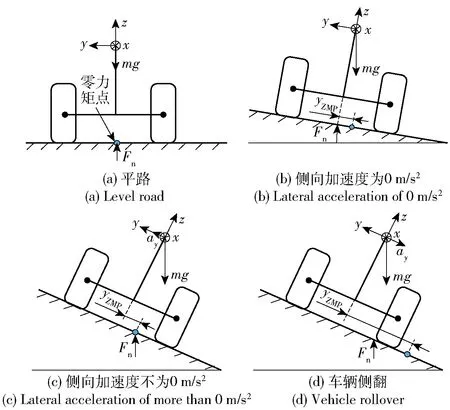
图4 零力矩点分布Fig.4 Zero moment point distribution

基于零力矩点的侧倾力矩平衡，可以得到

(16)

式中：φ为道路侧倾角；h为质心高度；Ix为车辆绕x轴的转动惯量。

对φ进行小角度假设，对(16)式进行近似线性化，可以得到零力矩点的横向偏移量yZMP的表达式为

(17)

参考车辆轮距的一半距离，对零力矩点的横向偏移量yZMP进行归一化处理，得到

(18)

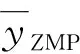
假设高速行驶的车辆前轮转角较小，即cosδf≈1,sinδf≈δf，构建满足以上需求的简化车辆动力学模型，如(19)式所示：

(19)

基于以上公式，得到的分布式电驱动车辆离散化非线性动力学方程为

y(k)=f(X(k),u(k)+ε(k))，

(20)

式中：y(k)为输出量，y=[β,ωr,ψ,yZMP,y,yr]T，k为时间序列；X为状态量，X=[β,ωrc,ωrf,ωr,vx,vy,ψ,yZMP,x,y,xr,yr]T；u(k)为控制量，u=[Mzc,Mzf]T；ε(k)为零均值白噪声。

3 横摆力矩控制器设计

NMPC具有解决多输入、多输出非线性系统的在线约束能力，通过状态预测，滚动优化和反馈求解可得到系统的实时最优控制量。但是，由于车辆实际行驶工况复杂、多变，当车辆系统出现大范围参数变化或是行驶状态突变时，NMPC缺乏针对环境的自适应能力。

本文提出一种基于数据驱动多模型预测控制的横摆力矩控制方法，将车辆局部多模型在线建模与控制预测量相结合，根据系统输入/输出数据库确定其当前工作点，在线构建系统的局部多模型。该控制系统结构框图如图5所示。图5中：y(k+λ+1|k)表示k为起始时刻，预测模型在k+λ+1时刻的输出量，λ为时刻；yr(k+1)为k+1时刻的期望输出量，r(k+λ+1|k)表示k为起始时刻，k+λ+1时刻的期望控制量；u(k+λ|k)为表示k为起始时刻，k+λ时刻的实际控制量；Δu(k+λ|k)表示k为起始时刻，k+λ时刻实际控制量的变化量。

图5 数据驱动多模型预测控制器架构Fig.5 Structure diagram of data-driven multi-model predictive controller

车辆非线性系统的局部多模型的在线建模问题可转化为如下求解优化问题：

(21)

结合(20)式和(21)式，构建局部模型加权形式为

(22)

基于CARIMA模型构建车辆的局部多模型系统，其表达形式为

(23)

式中：nA、nB、nC分别为局部模型输入量、输出量以及噪声干扰的阶数；Aj∈Rl×l;Bj∈Rl×l;Cj∈Rl×l.

引入增量形式，将(23)式的每一个局部辨识模型转化为

(q-1)Δy(k)=(q-1)Δu(k-1)+(q-1)ε(k)，

(24)

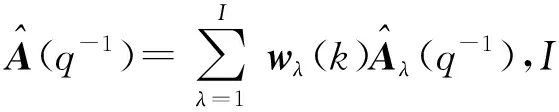
-1(q-1)(q-1)Δy(k)=
-1(q-1)(q-1)Δu(k-1)+ε(k).

(25)

为得到系统的多步预测输出方程，引入Diophantime方程，构建基于数据驱动局部多模型车辆系统在k+j时刻的最优控制预测输出表达式如下：

y(k+j)=Fj(q-1)y(k)+Gj(q-1)Δu(k+j-1)+
Hj(q-1)Δu(k-1)+Ej(q-1)ε(k+j)，

(26)

式中：Fj(q-1)=Fj,0+Fj,1q-1+…+Fj,nAq-nA；Gj(q-1)=G0+G1q-1+…+Gj-1q-(j-1)；Hj(q-1)=Hj,0+Hj,1q-1+…+Hj,nB-1q-(nB-1)；Ej(q-1)=E0+E1q-1+…+Ej-1q-(j-1).

基于以上分析，所构造的目标评价函数为

(27)

s.t.umin≤u(k+λ)≤umax，
Δumin≤Δu≤Δumax，
ymin≤y≤ymax，

式中：Q和R分别为被控系统输出量和输入量的加权矩阵；Np为预测时域；Nc为控制时域。

通过二次规划求解过程，选取控制序列中的第1个向量作为系统的最优控制输入量，循环滚动优化求解，得到车辆实时的附加横摆力矩为

(28)

4 最优驱动力矩分配控制器设计

底层转矩分配控制器可将附加横摆力矩转化为4轮最优驱动力矩，保证车辆操纵稳定性。针对极限、恶劣的越野行驶环境，本文基于轮胎纵向滑动率和轮胎垂直载荷转移设计最优驱动力矩分配控制器。假设车辆的静态质量均匀分布在4个车轮之间。根据转矩平衡方程，得到各车轮的转动力学方程为

(29)

根据(4)式和(13)式，可得到轮胎纵向滑动率动态方程如下：

(30)

分布式驱动电动车辆的4个车轮纵向驱动力矩均独立且可控，可得到由车辆纵向力产生的横摆力矩Mz的表达式为

(31)

车辆在越野环境下进行高速避障，考虑到路面的附着系数较低且道路起伏不定，每个车轮的垂直载荷转移对车辆的横向稳定性有很大的影响。因此，本文在协调各轮驱动力矩分配的过程中加入驱动轮垂直载荷转移变量因子，4个车轮的垂直载荷表达式为

(32)

式中：Fz1、Fz2、Fz3、Fz4分别为各轮的垂直载荷。

4个车轮的垂直载荷转移权重系数分别为

(33)

结合(26)式～(29)式，可得到考虑垂直载荷转移的纵向滑移率状态空间方程为

(34)

式中：S为状态向量，S=[s1,s2,s3,s4]T；U为控制向量，U=[T1,T2,T3,T4]T；Y为输出量，Y=Mz；Cl1、Cl2、Cl3、Cl4分别为左前轮、右前轮、左后轮、右后轮的轮胎纵向刚度。

构建的目标评价函数为

(35)

式中：e(t)表示实际状态观测值和期望状态值之间的偏差；e(t)表示系统保持期望值能力的权重系数矩阵；R(t)表示控制量约束的权重系数矩阵；t0、tf分别表示积分的起始时刻和终止时刻。

为避免轮胎力进入难以控制的非线性工作区域，减少打滑现象，轮胎滑动率和轮胎侧向力需要控制在一定的范围内。同时，车辆侧倾约束也是车辆操纵稳定性必须考虑的条件。由此构建的目标评价函数约束条件如下：

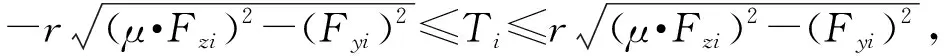
(36)

式中：Tmax为最大驱动力矩；Fymax为最大侧向力；smax为最大滑移率；μ为路面摩擦系数。

基于二次规划算法理论，将目标评价函数转化为标准二次型从而进行最优化求解：

(37)

式中：q为目标评价函数；G、C为标准二次型向量。

最终得到控制系统4个驱动轮实时的最优驱动转矩为

(38)

5 仿真验证

为验证本文分层协调操纵稳定性控制策略在提高分布式电驱动越野车的机动性和过弯横向稳定性的有效性，基于Carsim和Simulink软件联合仿真平台设计越野极限工况下的仿真实验，进行本文提出的控制策略、无控制以及传统MPC控制(仅考虑质心位置处的横摆运动模式)的对比实验验证。车辆模型参数如表1所示。

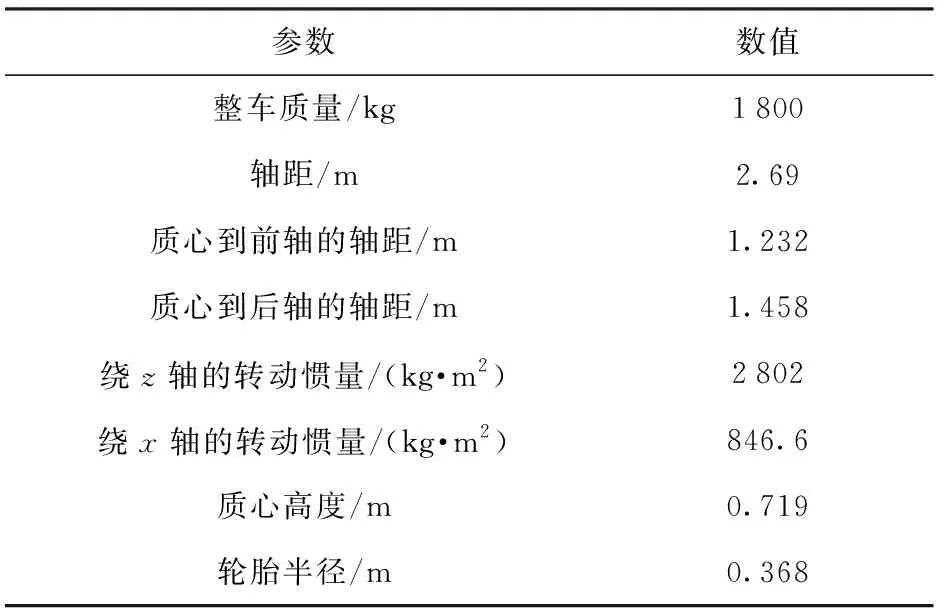
表1 车辆模型参数Tab.1 Vehicle model parameters

5.1 实验场景1

为验证车辆在极限工况下的高速避障稳定性和高机动性，选取标准双移线工况作为实验工况，车速设定为90 km/h，路面附着系数设定为0.35. 图6表示3种控制方式下车辆的轨迹跟踪能力。由图6可知：无控制的车辆出现较大侧滑，行驶轨迹严重地偏离期望轨迹，车辆处于失控状态；基于传统MPC的车辆基本可以保证安全行驶，但是在转弯处也出现了较大的超调；基于本文控制策略，车辆跟踪期望轨迹的准确度明显提升，最大横向偏离，具有较强的过弯姿态修正能力，基本没有出现过大的侧滑、甩尾的情况。由图7可知，相比于传统MPC，基于本文控制策略的车辆方向盘转角输入量更小其平滑，避免了过多转向，提高了乘车舒适性和安全性。图8和图9表示3种控制方式下车辆横摆角速度和质心侧偏角的对比情况，相比于传统MPC，基于本文控制策略的车辆实际横摆角速度和质心侧偏角更准确且迅速地跟踪期望值，车辆操纵稳定性明显提高。而无控制的车辆在此实验工况下已完全超出稳定区间，发生失稳的危险。图10表示车辆实时的零力矩点偏离情况，从中可知基于本文控制策略的车辆在横向稳定性控制中充分考虑到了车辆容易发生侧倾的情况，更有效地控制了零点力矩偏离距离。在图11中，基于本文控制策略，分布式电驱动车可根据实际行驶状态来实时调整各轮的驱动力矩，且输出量较为平滑，保持在合理的范围内，具有较高的机动性能。实验结果进行量化比较，3种控制方式的控制偏差量如表2所示。

图6 车辆轨迹Fig.6 Vehicle trajectory

图7 方向盘转角Fig.7 Steering wheel angle

图8 横摆角速度Fig.8 Yaw rate

图9 质心侧偏角Fig.9 Sideslip angle

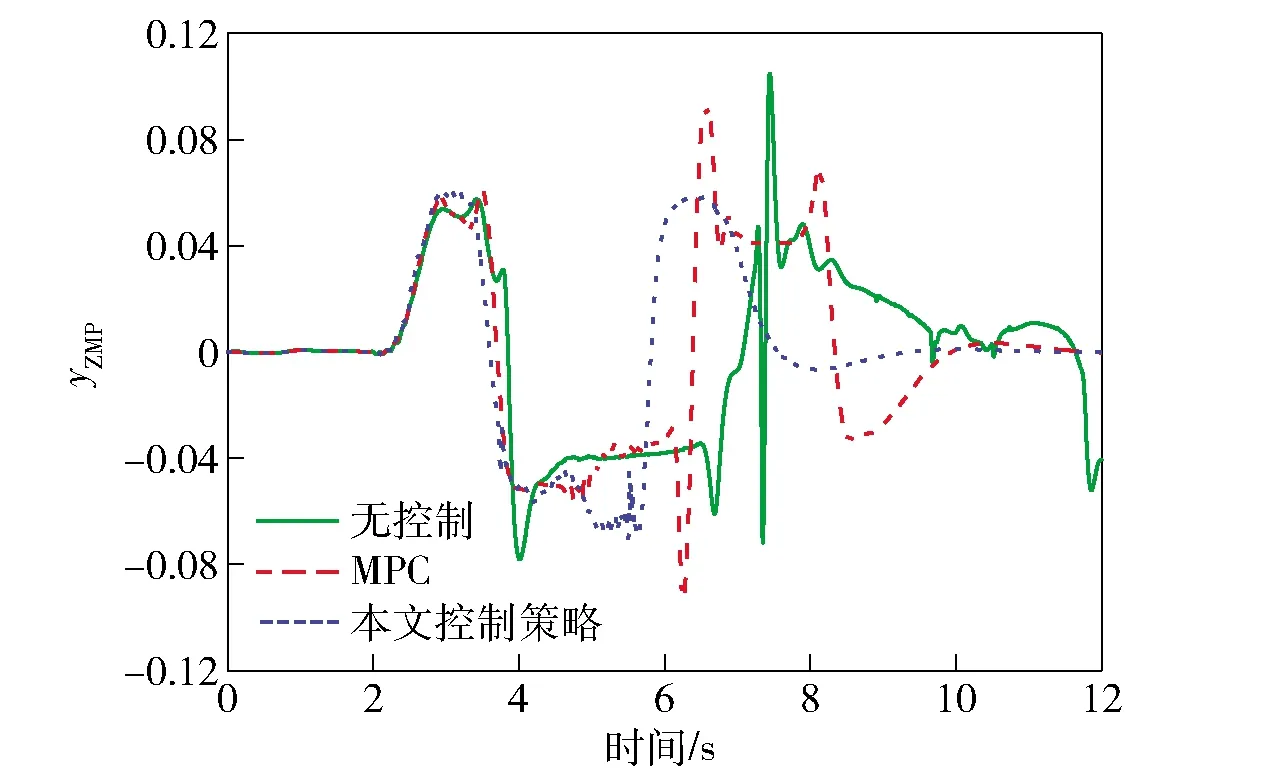
图10 零力矩点偏离距离Fig.10 Distance from the zero-moment point

图11 4轮转矩优化分配Fig.11 Four-wheel torque optimization distribution

表2 场景1仿真实验结果Tab.2 Simulation test results of Scenario 1

5.2 实验场景2

为验证车辆在具有时变道路曲率和侧向坡度角的低附着越野工况下的操纵稳定性，构建越野环境实验工况，选择Carsim自带的Alt 3 from FHWA工况，实验环境和道路侧向坡度如图12所示。实验车速设定为96 km/h，路面附着系数设定为0.5.

图12 实验道路Fig.12 Test road

由图13和图14可知，基于传统MPC的车辆在大曲率弯道、倾斜越野路面的转向过程中较容易发生侧滑等危险。在纵向坐标800 m处车辆偏离了期望的轨迹，方向盘转角输入量出现超调现象，控制效果不理想。而本文控制策略充分考虑了路面信息以及车辆过弯姿态信息，轨迹跟踪的准确度明显提升，方向盘转角输入量更加平稳。由图15和图16可知，相比于传统MPC，本文控制策略可以在极限越野工况下保证实际横摆角速度和质心侧偏角稳定在理想范围内，过弯横向稳定性明显提高。由图17可知，相比于传统MPC，基于本文控制策略的车辆可有效减小零力矩点偏离的距离，改善了越野车辆在极限工况下的侧倾稳定性。图18表示基于本文控制策略的各轮驱动力矩分配情况，可灵活且最优地得到实时驱动力矩最优值，高效提高了分布式电驱动越野车的机动性和过弯横向稳定性。将实验结果进行量化比较，3种控制方式的控制偏差量如表3所示。

图13 车辆轨迹Fig.13 Vehicle trajectory

图14 方向盘转角Fig.14 Steering wheel angle

表3 场景2仿真实验结果Tab.3 Simulation test results of Scenario 2

图15 横摆角速度Fig.15 Yaw rate

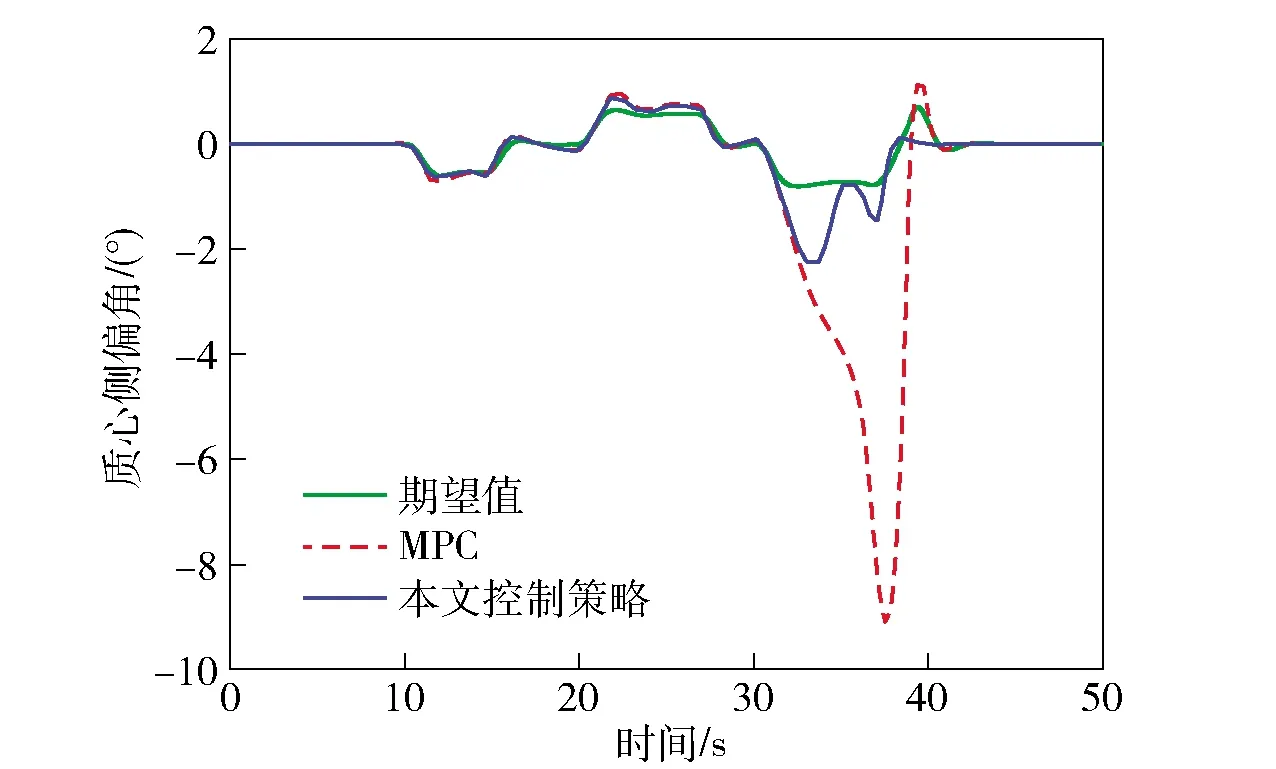
图16 质心侧偏角Fig.16 Sideslip angle

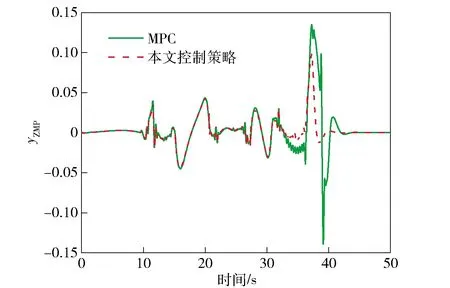
图17 零力矩点偏离距离Fig.17 Distance from the zero-moment point

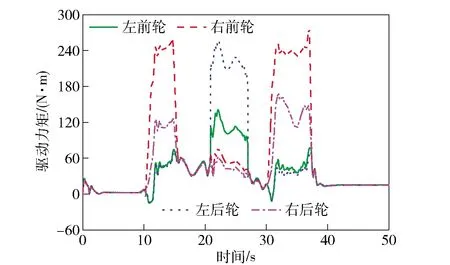
图18 4轮转矩优化分配Fig.18 Four-wheel torque optimization distribution

6 结论

本文以极限越野环境下分布式电驱动车辆为研究对象，提出了一种充分考虑道路信息和车辆过弯姿态信息的分层协调操纵稳定性控制策略，并通过Carsim和Simulink联合仿真平台验证策略的有效性。得到以下主要结论：

1)细化并重构了车辆横摆运动动力学方程，由于车辆横向失稳状态下存在不同程度的车身轨迹偏离，提出一种绕车辆质心处和前轴中心处的双层融合型附加横摆力矩协调控制方法，解决了传统控制方式过于保守或是激进，无法在车辆极限失稳危险情况下实现最优车身姿态修正反馈的问题，最大程度地发挥了分布电驱动车辆的避障机动性和路径保持能力。

2)考虑到越野工况存在时变道路曲率和侧向坡度角，在横向稳定性控制基础上加入侧倾稳定性约束条件，提出一种基于数据驱动多模型测控制的横摆、侧倾运动集成协调控制方法，改善了主动安全控制系统对极限工况的自适应能力，提高了车辆在复杂越野工况下的转向机动性和横向稳定性。

3)考虑到极限越野环境下路面附着系数较小以及路面颠簸，车辆高速转弯极易发生侧翻、侧滑甩尾等危险，本文基于轮胎滑动率和垂直载荷转移反馈信息获得最优的各轮驱动力矩控制量，最大程度地发挥了分布式电驱动越野车的快速通过能力和行驶稳定性能。